双激励二维超声振动切削装置设计

刘汇清，皮 钧，杨 光

（集美大学机械与能源工程学院，福建 厦门 361021）

1 引言

超声波椭圆振动切削技术最早由日本学者提出，通过特定的超声振动系统给刀具施加超声振动，可以使刀具的切削刃在切削过程中附加一个椭圆轨迹的超声频振动[1]。这种超声频振动可以有效降低切削力、切削温度，提高工艺系统刚度，改善工件的加工质量等优点[2-4]。超声波椭圆轨迹的产生是二维超声振动中的一个技术难题，国内外众多学者对此进行了大量的研究工作[5-8]。文献[9]将两组夹心式换能器以90°夹角的方式安装于特制的基座上，在两个同频且有一定相位差的正弦信号激励下，实现前端刀具的超声波椭圆振动。文献[10]研制出一种垂直型的椭圆轨迹发生装置，该装置中两组压电陶瓷晶堆正交分布并通过一个紧固螺栓将其固定在基体和刀杆之间，两个正交方向的振动通过刀杆结合并放大，在前端刀头上产生椭圆振动轨迹。文献[11]研制出一款V型结构的超声波椭圆振动装置，该装置中两组夹心式换能器以60°夹角的方式被一个V型结构固定在一起。紧固螺栓将尾座、V型结构、压电陶瓷晶堆和前质量块相连。两相振动通过前质量块结合并放大，在前端刀头上产生椭圆振动轨迹。

上述机构存在的共同缺陷是，两个方向的振动都要经过一个刚性金属机构结合并放大，才能最终合成前端刀头的椭圆振动轨迹，但由于刚性金属机构受到振动激励时，会使两路间存在很大的振动干扰，即一路会以负载的形式影响另一路，从而改变另一路的振型和固有频率。为了避免两路间的振动干扰，提出了一种新型的双纵向超声波椭圆振动系统，该系统采用柔性金属机构连接两支路，依靠柔性体很好的变形效果，避免了两支路间的振动干扰，从而使刀具前端能够合成理想的超声波椭圆轨迹。

2 双纵向超声波椭圆振动切削装置的设计及原理

该机构由纵向复合式换能器和工具组成，如图1所示。

机构设计：紧固螺栓将后盖板、压电陶瓷晶堆、前盖板（变幅杆）固定在一起构成纵向复合式换能器；将变幅杆输出端设计成45°斜面以便与矩形薄板连接，保证两组纵向复合式换能器的中心轴线在空间上相交且垂直。工具由矩形薄板和刀座组成，而刀座则固定在矩形薄板的中心位置。

基本原理：给两组换能器输入有相同频率且有一定相位差的正弦波电压，压电陶瓷片发生伸缩，使变幅杆本体发生纵向振动。两个正交方向的纵向振动耦合到矩形薄板，使薄板产生弯曲振动，并带动刀座做复杂轨迹运动，最终由两相振动叠加合成刀具前端的椭圆振动轨迹。

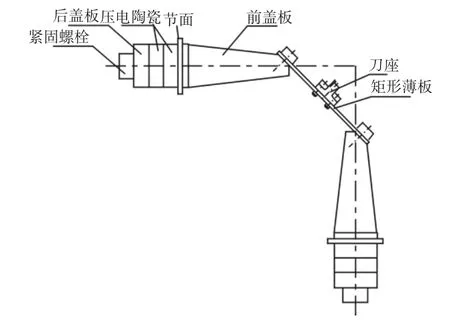
图1 垂直型双纵向超声波椭圆振动切削装置示意图Fig.1 Schematic Diagram of Vertical Double Longitudinal Ultrasonic Elliptical Vibration System

2.1 纵向复合式换能器设计

设计的纵向复合式换能器由λ/4换能器振子和λ/4圆锥形变幅杆组成。λ/4换能器振子部分只由压电陶瓷和金属后盖板两种材料组成；λ/4圆锥形变幅杆大端面前接平滑圆柱体，且圆柱体末端带有法兰盘，为一体结构。其中，节面位置在压电陶瓷和法兰盘之间的结合面处（以下简称节面在前）。为了提高换能器振子前后振速之比，选取45钢做后盖板，采用6061AL做前盖板；压电陶瓷材料选用PZT-4，它的压电常数和机电耦合系数比较高，可获得更高的效率。运用解析法对纵向复合式换能器进行初步设计[12]。λ/4换能器振子频率方程：

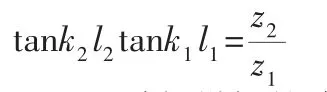
式中：k1—后盖板纵振的波数；

k2—压电陶瓷纵振的波数；

l1—后盖板长度；

l2—压电陶瓷堆总长度；

Z1—后盖板的特性声阻抗；

Z2—压电陶瓷材料的特性声阻抗。

λ/4变幅杆频率方程：

式中：k3—变幅杆圆柱体纵振的波数；k4—变幅杆圆锥体纵振的波数；l3—变幅杆圆柱体长度；l4—变幅杆圆锥体长度；R3—变幅杆大端面半径；R4—变幅杆小端面半径。

上述两式适用于纵向复合式换能器尾部后盖板暴露在空气中和变幅杆处于空载的情况，考虑到实际安装时，变幅杆前端连接有工具，即产出了负载作用，且实际加工时变幅杆上增加了法兰盘、螺纹孔。因结构复杂，传统解析法难以解决上述情况，故需要通过有限元方法进行精确求解。

2.2 工具设计

由于工具结构为不规则形状，很难采用解析法进行理论设计，因此，一般是通过有限元仿真的方法进行多次试验，反复修正尺寸，直到满足所需设计要求。矩形薄板采用强度高的钛合金材料Ti-6AL-4V，刀座采用45号钢。

工具设计的优点：矩形薄板具有很好的柔性，相对于刚体，它在受到两个方向的纵向振动激励时易产生弯曲变形，该变形避免了两组换能器之间（彼此作为负载）的振动干扰，易于合成超声椭圆振动轨迹。此外，刀座和矩形薄板之间，矩形薄板与前盖板之间拆装都很方便。

3 有限元仿真分析

对初步设计的双纵向超声椭圆振动系统进行模态分析，由于模型是装配体，所以采用Solidworks2013软件进行一体化建模，然后导入ANSYSWorkbench软件进行模态分析。

模态结果需满足：

（1）两个方向均为纵向振型；

（2）节面在前；

（3）仿真频率与设计频率相差很小。

在得到所需的模态结果之后，再对双纵向超声椭圆振动系统进行谐响应分析。

3.1 双纵向超声椭圆振动系统模态分析

模态分析的主要目的：确定双纵向超声椭圆振动系统的共振频率、振型和节面位置，为下一步的谐响应分析提供参考。模态分析用到的材料参数，如表1所示。

表1 材料参数Tab.1 Material Parameters

设计双纵向超声椭圆振动系统在空气中的谐振频率为50kHz，故提取频率范围为（43～52）kHz，通过模态分析，只得到1种振动模式，如图2所示。图2结果显示：（1）两个方向均为纵向振型；（2）节面在前；（3）共振频率为50514Hz，与50000Hz比较接近，误差为1.03%，考虑到刀具焊接到刀座后会使系统共振频率减小几百赫兹，故此误差可以接受。

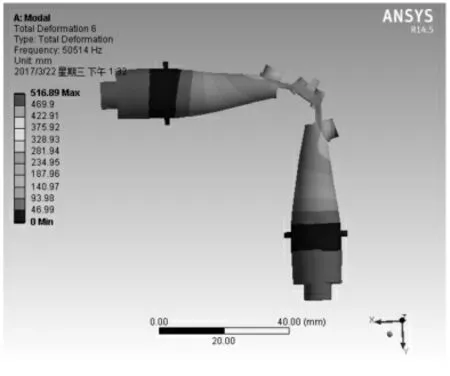
图2 一阶变形Fig.2 First Order Deformation

3.2 双纵向超声椭圆振动系统谐响应分析

谐响应分析主要研究：双纵向超声椭圆振动系统在受到两路正弦激励（激励随时间呈正弦规律变化）后产生的位移响应。

选取五组不同相位差的正弦载荷，载荷施加在压电陶瓷片与后盖板的交界面上，对刀头输出端一点做相位响应分析，并将双激励源参数和相位响应结果，如表2所示。

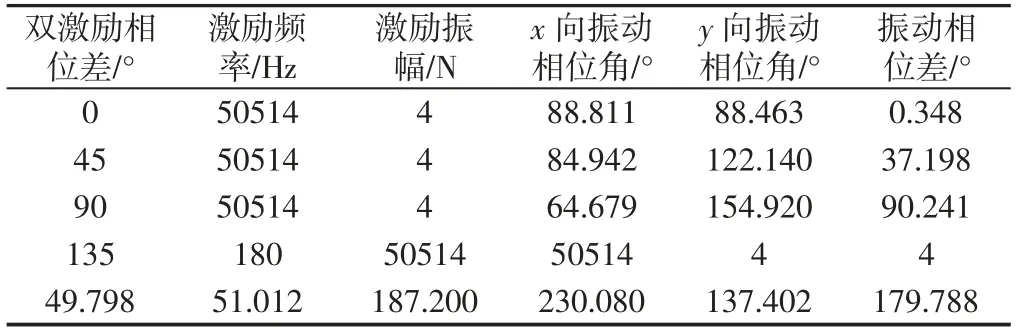
表2 双激励源参数与相位响应结果Tab.2 Double Excitation Source Parameters and Phase Response Results

从上表可知：当施加正弦激励相位差分别为0°、45°、90°、135°、180°时，对应的刀头输出端两相振动相位差近似为0°、37°、90°、137°、180°。即输出的两相振动相位差和输入的两相激励相位差非常接近。图3～图7中（a）、（b）分别为刀座输出端一点在x方向、y方向的相位响应；图3～图7中（c）表示利用MATLAB软件根据两相振动位移数据拟合的刀具运动轨迹。

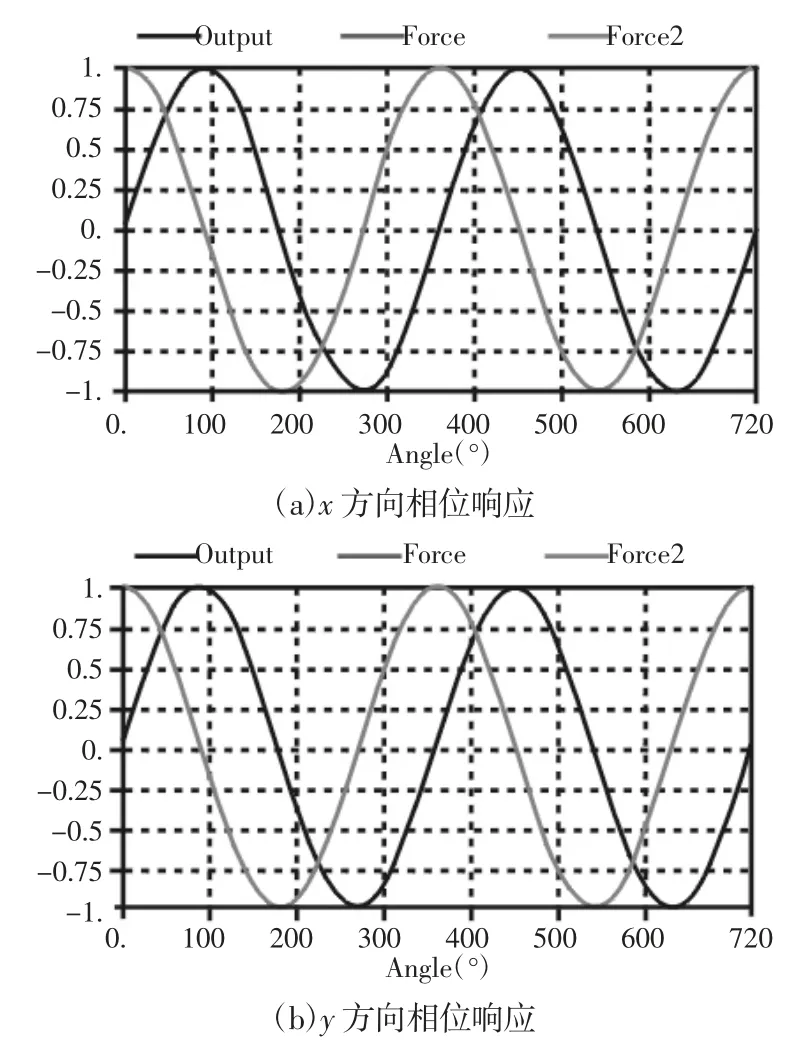
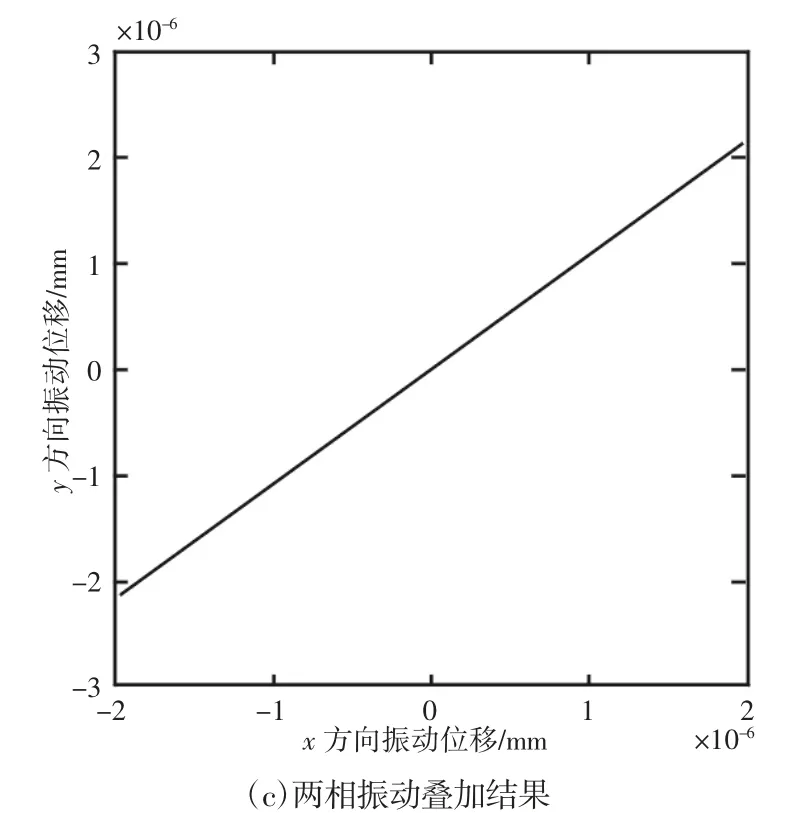
图3 激励相位差0°时的相位响应Fig.3 Phase Response when the Excitation Phase Difference is 0°

图4 激励相位差45°时的相位响应Fig.4 Phase Response when the Excitation Phase Difference is 45°

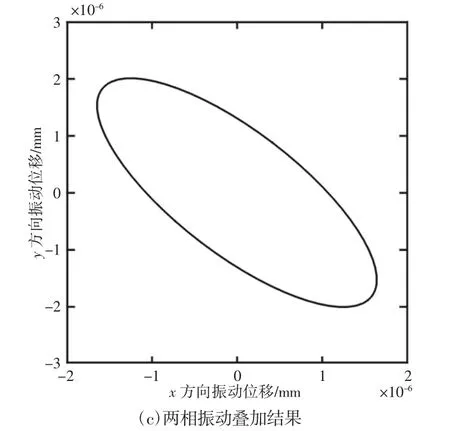
图6 激励相位差135°时的相位响应Fig.6 Phase Response when the Excitation Phase Difference is 135°

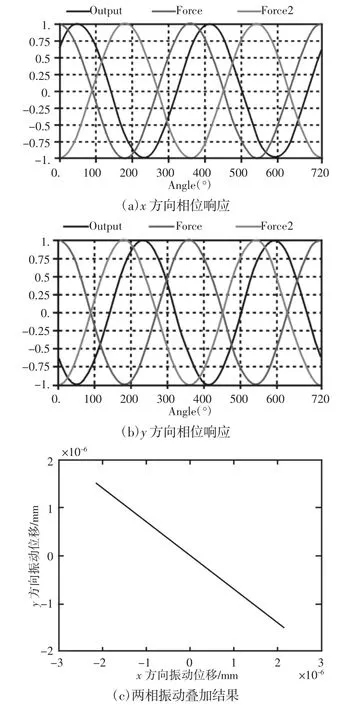
图7 激励相位差180°时的相位响应Fig.7 Phase Response when the Excitation Phase Difference is 180°

据图3～图7可得：

（1）两相振动轨迹均为正弦谐振曲线；

（2）两相振动叠加可以合成椭圆轨迹；

（3）当输入的两相激励相位差为0°时，输出的两相振动相位差也为0°，两相振动叠加为一条直线；

（4）当两相激励相位差由0°增至90°时，两相振动相位差也由0°增至90°，椭圆由扁平趋向饱满，椭圆短轴逐渐增大且与y轴正向夹角逐渐减小为0，椭圆长轴与x轴正向夹角逐渐减小为0；

（5）当两相激励相位差由90°增至180°时，两相振动相位差也由90°增至180°，椭圆由饱满趋向扁平，椭圆短轴逐渐减小且与y轴正向夹角逐渐增大，椭圆长轴与x轴正向夹角逐渐增大。

4 结论

（1）提出一种垂直型的双纵向超声波椭圆振动系统，该系统中工具端采用柔性矩形薄板的设计，避免了正交两路纵向复合式换能器之间的振动干扰，使各自振型输出形态良好；（2）对双纵向超声波椭圆振动系统进行模态分析和谐响应分析，能够实现超声波椭圆振动；（3）刀具端输出的两相振动相位差与双纵向超声椭圆振动系统输入的两相激励相位差与非常接近，可以通过调节输入的两相激励相位差来调整产生的椭圆轨迹倾斜度，从而控制轨迹变化满足曲线轨迹加工。