四轮转向车辆的直接横摆力矩控制研究

田 燃，肖本贤

（1.合肥工业大学工业与装备技术研究院，安徽 合肥 230009；2.合肥工业大学电气与自动化工程学院，安徽 合肥 230009）

1 引言

随着社会的发展，人们的出行方式越来越多样化，汽车作为人们目前主要的出行方式在人们的日常生活中扮演着重要的角色[1]。为了人们的出行方便，交通道路设施越来越完善，车辆的技术也不断的提高，汽车在交通工具中占有的比例也越来越大，行驶速度也不断的提高，给人们带来出行便利的同时，也带来了频繁发生的交通事故，其中很多事故都与汽车的稳定性有关，因此如何提高车辆行驶的稳定性成为当下人们急需解决的问题[2]。四轮转向是改善车辆在行驶中的稳定性的一种有效的控制方法，而直接横摆力矩控制（简称DYC，DirectYaw-momentControl）策略是为了减轻驾驶员的操作负担，提高车辆在各种复杂工况下的操纵稳定和行驶安全性。它的基本原理是通过调节车轮的受力状态，让车辆在行驶过程中产生附加的横摆力矩抑制过度转向或不足转向，从而主动地对车辆的稳定性进行控制，改善车辆在各种行驶条件下的操纵稳定性[3]。因此采用四轮转向与直接横摆力矩相结合的控制策略，运用七自由度车辆模型，考虑到滑模变结构控制算法具有简单、鲁棒性较强等优点，根据七自由度模型和理想模型之间的误差，设计滑模控制器主动控制附加的横摆力矩、后轮转角输出，并与不同的控制策略进行仿真对比，验证所设计的控制策略的有效性。

2 七自由度动力学车辆模型

2.1 整车动力学模型

为了充分地反映汽车行驶时的性能，及车轮在各种受力下的车辆的状态信息，建立七自由度四轮转向车辆模型。其中包括车身纵向、侧向、横摆运动，以及四个车轮的转动，忽略了车辆的侧倾、俯仰及垂直运动。假设汽车质心与汽车运动坐标系原点重合，不考虑转向系统的作用，以车轮转角作为整车动力学模型的输入，并认为前左右轮和后左右轮分别相等，建立七自由度四轮转向模型，如图1所示。

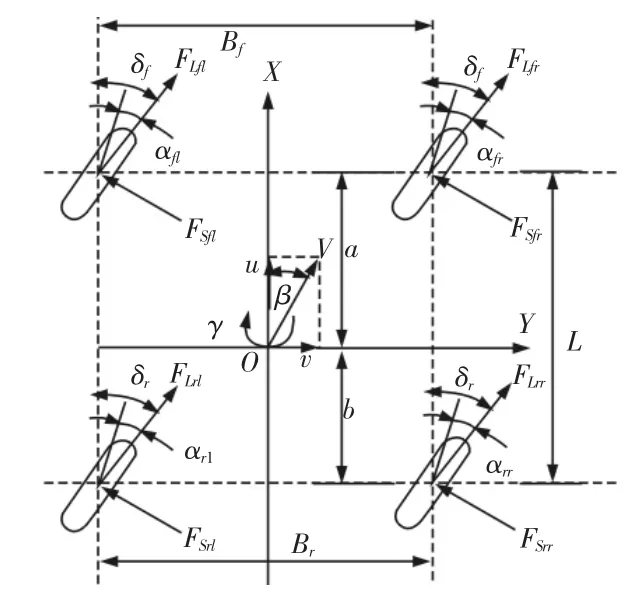
图1 七自由度车辆动力学模型Fig.1 Dynamic Model of Seven Degrees of Freedom Vehicle

图中：坐标系X，Y与车体固定；O—汽车质心；a、b—质心到前、后轴的距离；L—轴距L=a+b；Bf、Br分为前轴、后轴轮距；δf、δr—汽车的前、后轮转角；β—质心侧偏角；αi（u=fl、fr、rl、rr）—各轮的轮胎侧偏角；γ—横摆角速度；V—汽车质心速度；u—纵向车速；v—侧向车速；FLi（i=fl、fr、rl、rr）—车轮上的纵向力；FSi（i=fl、fr、rl、rr）—车轮上的侧向力。

由图1得车辆的动力学方程如下[4]：

侧向运动：

横摆运动：

纵向运动：

车轮的转动：

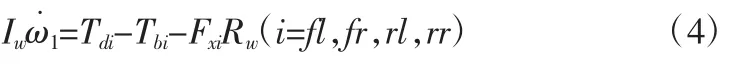
式中：m—整车的质量；ωi—各车轮的转动角速度；Fxi—各车轮在x轴上的纵向力；Tdi—车轮上驱动力矩；Tbi—车轮上制动力矩；Rw—车轮滚动半径；Iw—车轮转动惯量；Iz—整车绕Z轴的转动惯量；∑Fyi—车轮上的纵向力在y轴分量总和；∑Mzi—横摆力矩和；∑Fxi—车轮上的纵向力在x轴分量总和，即：

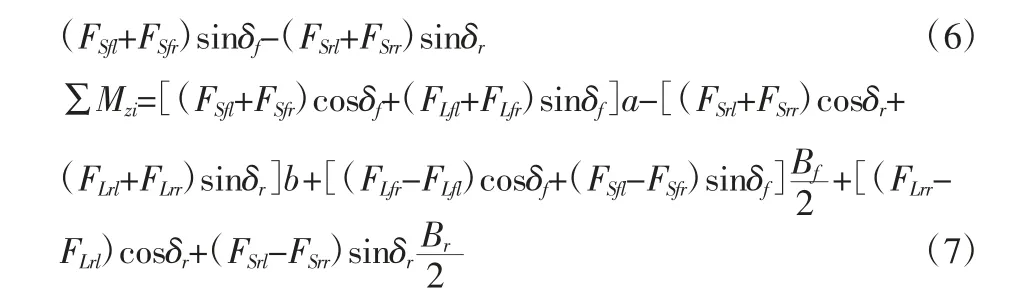
2.2 轮胎动力学模型

考虑轮胎对车体模型的非线性影响，采用Dugoff轮胎模型计算车辆行驶中的纵向力与侧向力[5]。

忽略了回正力矩作用，Dugoff轮胎模型轮胎的纵向力Fxi和侧向力Fyi分别为：

式中：Ci，Cα—轮胎的纵向刚度和侧向刚度，其余的参数计算公式如下。

式（8）中轮胎侧偏角αi（i=fl，fr，rl，rr）大小根据运动学分析表示为：

式（8）中各个车轮的滑移率Si（i=fl，fr，rl，rr）为：

式（10）中各车轮上的纵向速度ui（i=fl，fr，rl，rr）为：

式（8）中f（γ）为：

其中

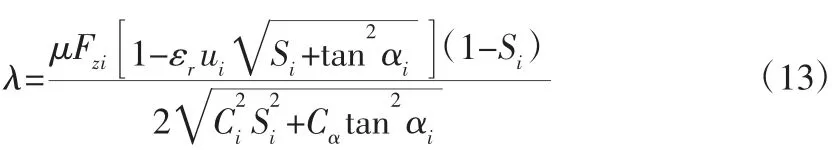
式（13）、式（14）中，εr为地面粘着减少系数，Fzfl、Fzfr、Fzrl、Fzrr分别为左前轮、右前轮、左后轮和右后轮的垂向作用力；h为质心高度；ax和ay分别是车辆的纵向加速度和侧向加速度，μ为地面附着系数。

3 理想转向模型

理想模型是驾驶员输入方向盘操纵信号，车辆产生期望的动态输出响应信号[6]。四轮转向车辆的控制目标一方面是零化质心侧偏角，以保证车辆转向时拥有良好的行驶轨迹和车身姿态；另一方面要求横摆角速度能在不同工况下跟踪理想值，提高车辆的瞬态响应和操纵稳定性。目前大多数理论都以线性二自由度车辆的行驶状态为理想转向特性。由此，在线性二自由度车辆模型基础上考虑一阶惯性环节，将得到理想转向特性[7]。线性二自由度前轮转向数学模型为：

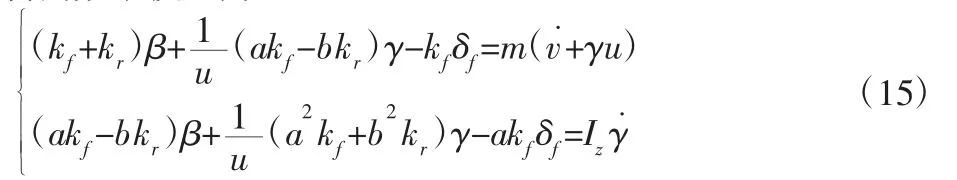
式中：kf、kr—前、后轮等效侧偏刚度（两侧轮胎之和）；令初始条件为零，求得横摆角速度γ的传递函数为：

由式（15）第二式可知，当质心侧偏角β趋于零时，横摆角速度γ为前轮输入转角的一阶滞后响应，因此式（16）可写成如下标准形式：

因为质心侧偏角β趋于零，所以β的传递函数为：

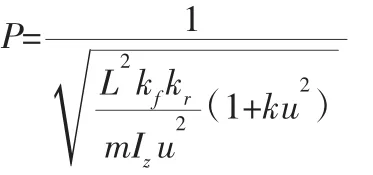
式中：K—稳定性因数；Te—一阶惯性环节时间常数，则理想转向模型的状态方程为：

式中：γd—车辆理想横摆角速度；βd—车辆理想质心侧偏角；δ*f—理想车辆模型前轮输入转角。

4 滑模控制器设计

4.1 滑模控制律设计

控制系统的结构图，如图2所示。设计滑模控制器产生车辆转向所需的横摆力矩M和后轮转角，将滑模控制器产生的横摆力矩M以制动力矩的形式分配到车辆的四个轮子上，通过制动力矩的分配以及转向角的修正，使车辆转向行驶时的横摆角速度和质心侧偏角跟踪理想模型。

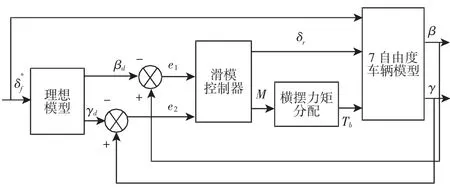
图2 控制系统结构图Fig.2 Control System Structure

加入附加横摆力矩的四轮转向线性二自由度数学模型可以表示为：

式中：kf、kr—前、后轮等效侧偏刚度（两侧轮胎之和）；M—附加的横摆力矩。式（20）写成状态方程的形式为：

由式（19）、式（21）定义状态跟踪误差为：

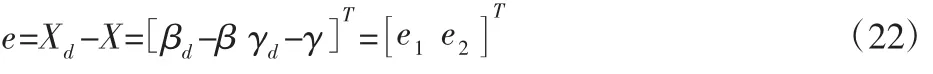
对式（22）求导，并结合式（19）、式（21）可得：

为了补偿模型的不确定性和提高跟踪控制精度，滑模面选择积分滑模面[8]：

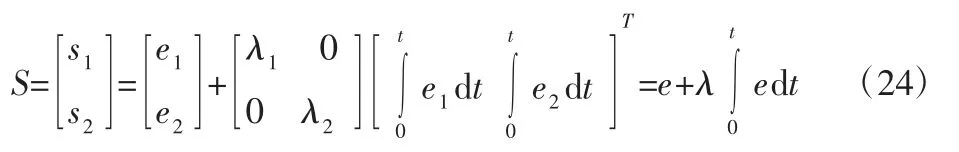
式中：λ—正定对角矩阵。对式（24）求导可得：

为了实现滑动模态，采用如下的指数趋近律控制方式：

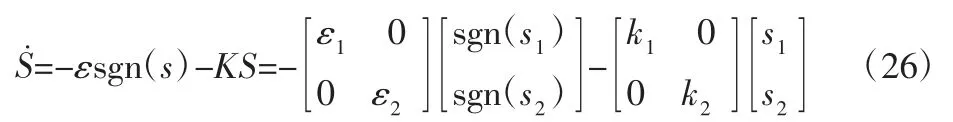
式中：K—对角增益矩阵；k1、k2—正数。由于矩阵B满秩可逆，联合式（23）、式（25）、式（26）得到控制律：

4.2 控制算法稳定性分析

定义李雅普洛夫（Lyapunov）函数为

对式（28）求导，并结合式（26）、式（27）可得：

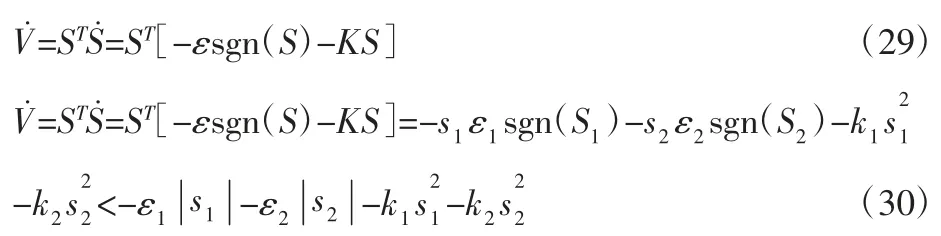
从式（30）可看出，当由于指数趋近律k1，k2都为正数，V˙<0。根据李雅普洛夫（Lyapunov）定理，可知此时系统稳定。

4.3 滑模控制抖振抑制

滑模控制律中并不存在理想的开关特性，因此变结构系统在不同的控制逻辑中来回切换时容易产生抖振，抖振不能彻底消除，但是可以尽可能的抑制抖振[9]。为了便于控制器设计，采用连续函数来代替符号函数sgn（Si）抑制抖振，即：

式中：ρ—一个很小的正常数，这样滑模控制律可以写成：

5 横摆力矩的分配

为了提高车辆的极限行驶性能，采用单侧制动策略，即所需附加的横摆力矩由左侧或者右侧车轮产生。为了将滑模控制器产生的附加的横摆力矩M分配到需要制动的一侧车轮，通过如下方法判断，如表1所示。

表1 制动力矩分配策略Tab.1 Scheme of Brake Force Distribution

为了更充分利用单侧车轮的制动力，根据车轮载荷对前、后轮的制动力进行分配，M为滑模控制器产生的车辆失稳时所需附加的横摆力矩，假设右侧车轮被制动，则有：

因为前后轴距离基本相等，则：

式中：F1，F2—前右轮、后右轮制动力。考虑到在车轮未抱死时，轮胎制动力与载荷近似成比例关系，而汽车在行驶过程中又存在着负荷转移，为了充分利用路面附着系数，可按下式进行制动力分配。

轮胎制动力确定以后，则右侧车轮需要附加的制动力矩为：

同理，汽车左侧车轮制动力及所需制动力矩也按上诉方法进行分配。

6 仿真结果及分析

为了对比四轮转向与横摆力矩控制相结合的控制效果，同时进行了相同条件下的比例控制4WS汽车时域响应仿真，典型的比例四轮转向系统采用的是零质心侧偏角策略[10]。采用Matlab/Simulink仿真，仿真分为两部分：第一部分在汽车前轮转角阶跃输入工况下仿真；第二部分在汽车前轮转角正弦输入工况下仿真。

6.1 阶跃工况仿真

阶跃工况用阶跃信号作为前轮转角输入，幅值为5度（0.087rad），从2s开始起跃，整个仿真时间为10s，路面附着系数0.9，汽车初始速度取80km/h。滑模控制器的积分滑模面参数λ=diag（2，4），指数趋近律参数ε=diag（0.6，0.6）、K=diag（0.2，0.2），连续函数的参数ρ=0.02。仿真中四转向汽车的主要参数，如表2所示。

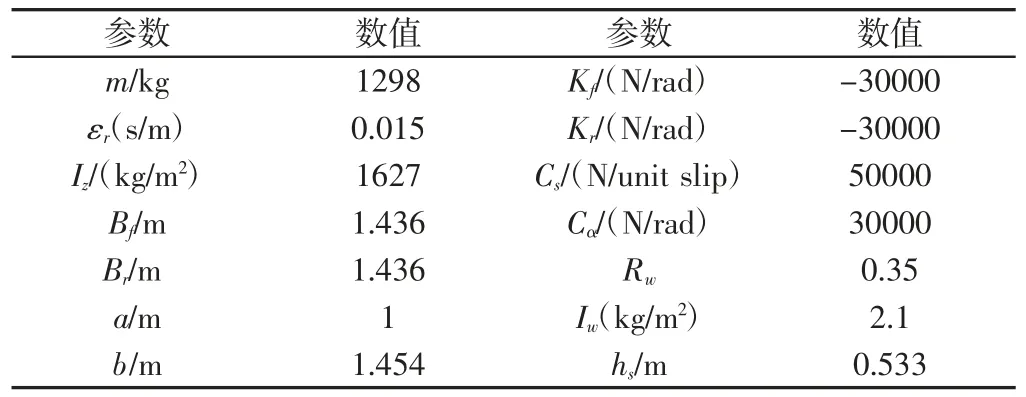
表2 汽车主要参数Tab.1 The Main Parameters of the Car

在高速阶跃工况时，施加在汽车左侧车轮上的附加制动力矩和附加的后轮转角，如图3、图4所示。由图5可知，由于对汽车左侧车轮施加了制动力矩，抑制了车辆过度转向，横摆力矩控制4WS汽车横摆角速度幅值与理想值基本保持一致，提高了汽车在高速下操纵稳定性，使驾驶员在高速有更好的驾驶安全感，验证了横摆力矩分配的有效性；比例控制4WS汽车横摆角速度幅值较大，不利于高速转向。由图6可知，横摆力矩控制4WS汽车的质心侧偏角基本为零，能够保持很好的车身姿态，汽车的平稳性得到提高；比例控制4WS下的汽车质心侧偏角幅值较大。

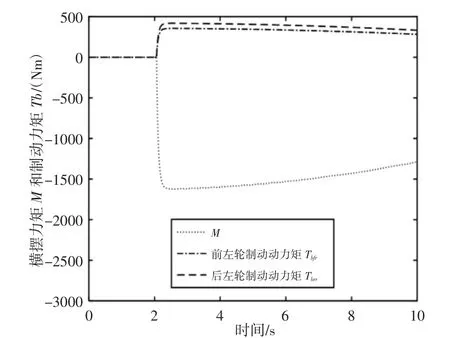
图3 横摆力矩M和左侧车轮附加制动力矩TbFig.3 Yaw Moment Mand Left Wheel Additional Braking Torque Tb

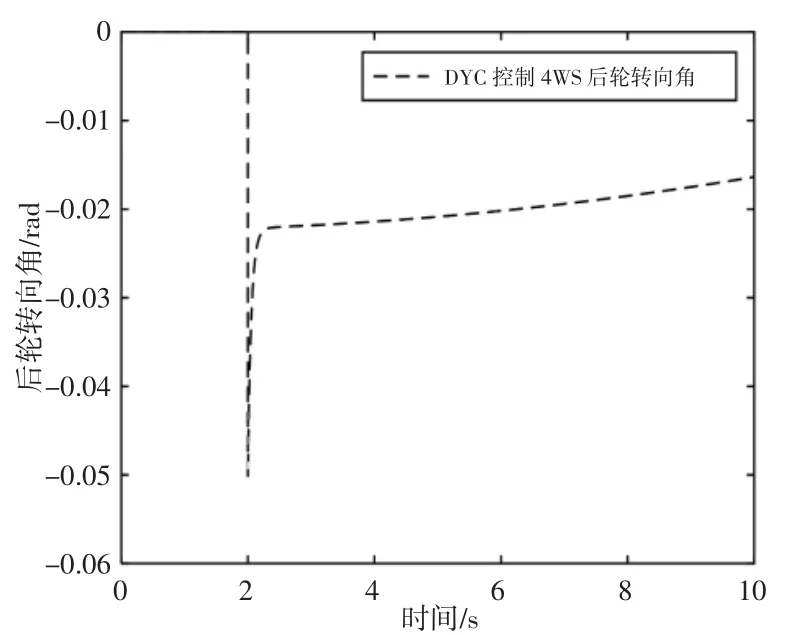
图4 附加后轮转角Fig.4 Additional Rear Wheel Steering Angle

图5 横摆角速度响应Fig.5 Yaw Rate Response

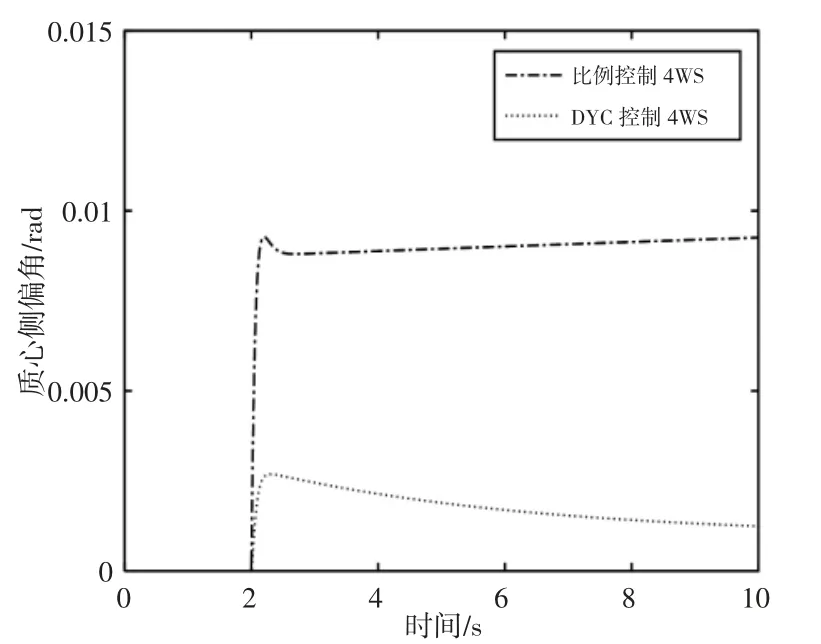
图6 质心侧偏角响应Fig.6 Side Slip Angle Response

6.2 正弦工况仿真

正弦工况用正弦的信号作为前轮的转角输入，幅值为5°（0.087rad），周期为4s，即从2s开始，6s结束，其它参数与阶跃仿真工况一致。在高速正弦工况下，施加在汽车右侧、左侧车轮上的附加制动力矩和附加的后轮转角，如图7～图9所示。由图10可以看出，整个转向过程中，由于分别对汽车右侧和左侧车轮施加了制动力矩，抑制了整个转向中不足转向，使横摆力矩控制4WS汽车横摆角速度幅值与跟踪理想值基本一致，提高了极限驾驶的安全感，控制效果好于比例控制下4WS汽车，验证了横摆力矩分配的有效性。由图11可知，横摆力矩控制4WS汽车质心侧偏角稳态值一直保持非常小，接近于零，只有小幅度的波动；比例控制4WS汽车质心侧偏角的值也得到了减小，但是比横摆力矩控制4WS的质心侧偏角大。

图7 横摆力矩M和右侧车轮附加制动力矩TbFig.7 Yaw Moment Mand Right Wheel Additional Braking Torque Tb

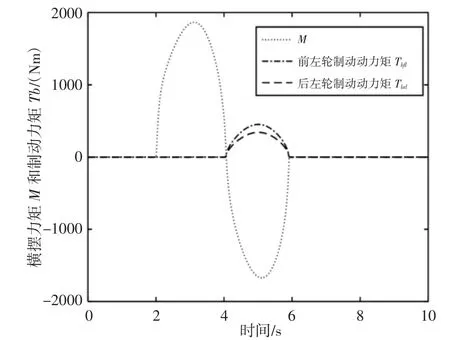
图8 横摆力矩M和左侧车轮附加制动力矩TbFig.8 Yaw Moment Mand Left Wheel Additional Braking Torque Tb

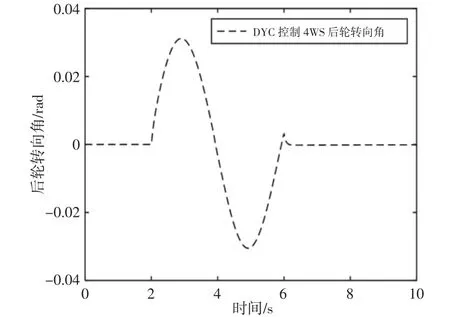
图9 附加后轮转角Fig.9 Additional Rear Wheel Steering Angle

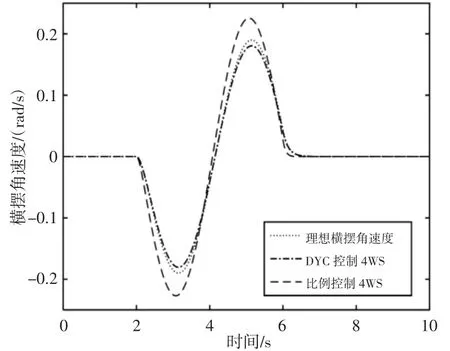
图10 横摆角速度响应Fig.10 Yaw Rate Response

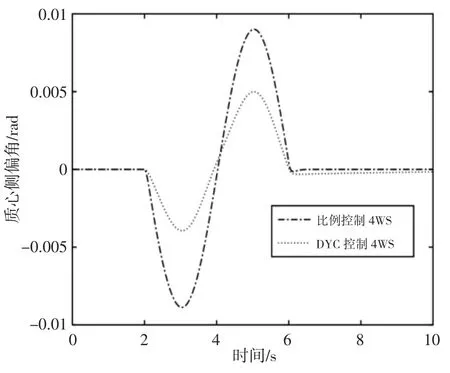
图11 质心侧偏角响应Fig.11 Side Slip Angle Response

7 结论

对基于横摆力矩控制和四轮转向相结合控制策略进行研究，设计滑模控制器产生车辆转向所需的横摆力矩和后轮转角，将滑模控制器产生的横摆力矩按单侧制动力矩的形式分配到车辆的四个轮子上，通过制动力矩的分配以及转向角的修正跟踪理想转向模型的质心侧偏角和横摆角速度，提高汽车极限工况下的行驶稳定性。通过阶跃和正弦不同工况下的仿真结果表明：比例控制下汽车的横摆角速度和质心侧偏角虽然得到了改善，但是在高速下还是容易出现危险，影响驾驶员的驾驶体验。相比较比例控制策略，基于横摆力矩控制和四轮转向相结合控制策略可以有效提高汽车的操纵稳定性，在高速时起到了良好的控制效果，改善了高速驾车的安全性，减轻驾驶员的操作负担。