基于多目标拓扑优化技术的齿轮结构优化设计

戴护民

（广东机电职业技术学院先进制造技术学院，广东 广州 510550）

1 引言

齿轮因具有稳定的传动比而在传动装置中为重要的传动件之一，齿轮结构性能的好坏不仅影响其工作寿命，也影响了传动装置的性能。随着工业制造的要求不断提高，对工程师设计出性能良好且节省材料的传动件也提出了较高的要求。目前，相关学者对齿轮结构优化设计做了大量研究并取得了一定成果，如文献[1]对齿轮齿条进行逻辑齿廓方程构建，运用Matlab得出最优的齿廓参数。文献[2]对斜齿轮减噪进行对角修形优化设计，设计出了承载时重合度较高的斜齿轮且降噪显著。

近年来，国内学者已将结构优化技术引入到齿轮结构设计过程中，但对于齿轮结构的设计研究仍停在单目标的概念设计阶段或尺寸参数化设计。然而，由于齿轮工作环境的复杂性，单目标优化仅能改善某一方面的性能，不能改进其总体性能。近年来，虽多目标优化设计在工程结构设计中有所应用，但在齿轮结构优化中的应用几乎没有[3-5]。

为了所设计的齿轮既能满足一定的力学特性又具有抑制外界激励的能力，提出一种可行的现代优化设计方法[6]改善齿轮结构的刚度和一阶固有频率，使其延长齿轮结构使用寿命。

引入了多目标理论和优化设计技术[7-8]，对冷弯成型机的直齿轮结构进行多目标拓扑优化设计，使直齿轮改善刚度和一阶固有频率，同时，还实现结构的轻量化设计。多目标拓扑优化中，主要采用折衷规划法构建关于柔度和一阶固有频率的SIMP多目标优化模型。为了能科学性地获得各子目标函数的加权因子，运用层次分析法求解各目标的加权因子。

2 齿轮有限元前处理及工况分析

以齿轮为研究对象，齿轮材料为45钢，材料属性和几何设计参数，如表1所示。

表1 齿轮的材料属性表Tab.1 Material and Property Parameter of Gear

齿轮孔与主轴通过键连接，对齿轮孔运用RBE2单元进行耦合并作为固定约束。齿轮的啮合运动使接触处受到集中载荷，依据冷弯成型生产线工作过程中测得该集中载荷使齿轮受到关于轴心的扭转为200N.m。基于HyperMesh对齿轮进行尺寸为4mm的网格划分，得到31680个六面体单元和2624个五面体单元，如图1所示。

图1 齿轮结构有限元模型及工况条件Fig.1 Finite Element Model of Gear and its Loadstep

3 单目标拓扑优化模型构建

3.1 静刚度拓扑优化模型

为了所设计的齿轮结构具有足够的刚度来克服啮合传动时的接触应力，节省齿轮结构的使用材料。以单元材料密度值ρe为设计变量，以柔度最小化为优化目标，以优化前后体积比为约束条件构建齿轮的固体各向同性材料惩罚法（SMIP）优化模型。SIMP法是将有限单元作为一种人工材料密度并引入惩罚因子与材料弹性模量构建成函数关系：

式中：E0—单元e的弹性模量；ρe—单元e的相对密度，0<ρmin≤ρe≤1且ρmin是空洞处的最小密度值，为了避免优化求解中的奇异现象；E0—初始材料弹性模量；p—密度惩罚因子，常取p=3，中间密度材料的惩罚因子p的取值范围如下式：

式中：μ0—给定材料的泊松比，常取值为0.3。

式（1）是单元密度与材料弹性模量间的显性非线性关系，优化过程中引入惩罚因子p对单元密度值进行“惩罚”，使优化结果的中间密度单元能有效地实现0或1的二值化，得到较清晰边界。鉴于此，采用SIMP法构建的齿轮结构静态优化模型：

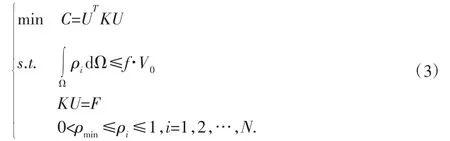
式中：C—结构柔度值；U—外载荷作用下的位移；K—齿轮整体刚度；f—优化前后体积比；V0—齿轮初始体积；ρi—第i个单元密度；ρmin—单元最小密度值，取ρmin=0.001。避免刚度矩阵发生奇异。KU=F—平衡方程，由齿轮受边界约束和外载荷所得。—体积约束，—优化后结构体积。C=UTKU—目标函数，由C=FTU并依据平衡方程所得。

3.2 静刚度优化结果

运用OptiStruct进行优化求解，经过35步优化迭代可得齿轮静态拓扑优化后的材料分布情况，如图2所示。

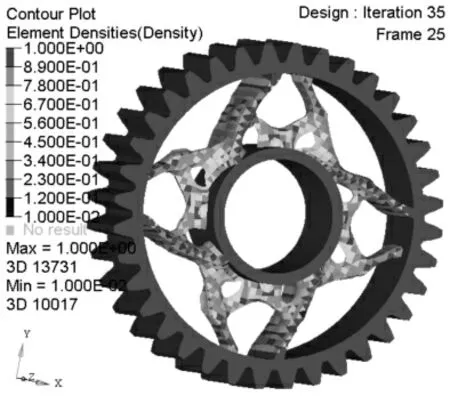
图2 直齿轮静态拓扑优化结果Fig.2 Static Topology Optimization Result of Gear

优化迭代后，直齿轮柔度最大值和最小值，如表2所示。

表2 优化前后齿轮柔度参数表Tab.2 Com pliance of Gear Before and After Optim ization

通过对齿轮的静态柔度拓扑优化可得，齿轮柔度值从2.595825mm/N明显下降到1.748555mm/N，齿轮的整体质量从2.38kg下降到0.714kg，如表2所示。

3.3 模态拓扑优化模型

模态拓扑优化主要是将工程师所关心的结构低阶固有频率进行改进，因结构低阶固有频率易接近外界激励而引起“共振”现象。以单元材料密度值ρe为设计变量，以一阶固有频率最大化为优化目标，以优化前后体积比为约束条件构建齿轮的模态优化模型并基于OptiStruct进行优化求解。然而，优化过程中因单元材料的去除使空洞区域边界的相邻阶次频率出现震荡病态现象，为了改进该问题，依据文献[9]的平均特征值原理对优化目标进行修正并得模态优化模型：

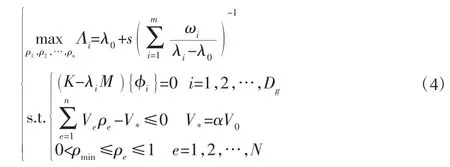
式中：Λi—修正的第i阶特征值；

λi—第i阶特征值；

ωi—第i阶对应的加权值；

s、λ0—给定的参数；

K—总刚度矩阵；

Dg—总自由度数，取i=1；

m—需要优化的阶次，取m=1。

3.4 模态优化结果

运用OptiStruct进行优化求解，经过39次迭代步得模态拓扑优化后齿轮结构的材料分布形式，如图3所示。

图3 直齿轮模态拓扑优化结果Fig.3 Modal Topology Optimization Result of Gear

通过优化前后对齿轮的模态特性比较，其一阶固有频率和质量，如表3所示。

表3 优化前后直齿轮一阶固有频率参数表Tab.3 First Order Natural Frequency of Gear Before and After Optim ization

通过对齿轮的模态一阶固有频率拓扑优化可得，齿轮一阶固有频率从582.4443Hz明显上升到857.2964Hz，齿轮的整体质量从2.38kg下降到1.14kg，如表3所示。

4 齿轮多目标拓扑优化模型构建

4.1 多目标优化模型

对直齿轮的多目标拓扑优化主要依据前文的优化目标和优化结果参数等构建多目标优化函数，并以多目标优化函数最小化，以优化前后的体积比为约束条件进行优化求解，使多目标优化的直齿轮不仅能改善其静态刚度和模态一阶固有频率等特性，还实现齿轮结构的轻量化设计。采用折衷规划法和平均频率法构建的多目标优化函数为：

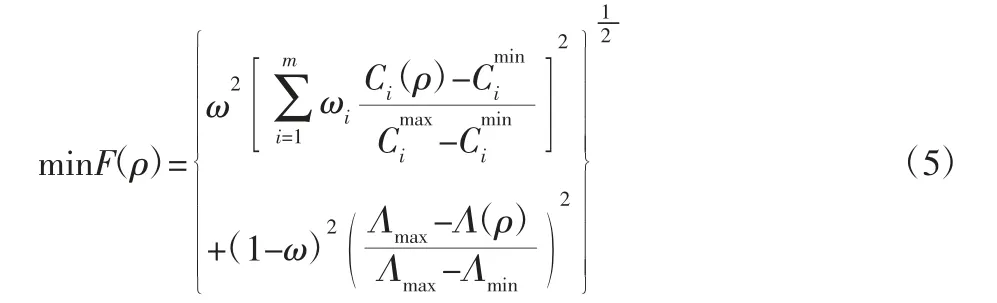
运用数理学决策论中的层次分析法确定多目标函数中静态柔度和模态一阶固有频率的加权因子，依据文献[10]构建决策矩阵为：

式中：S11、S12—静态柔度目标函数的相关元素；M11、M12—模态一阶固有频率目标函数的相关元素；依据文献[10]可得主对角线元素。

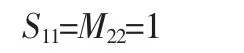
因齿轮需一定的刚度来确定传动的稳定性且其相对动态特性更为主要，依据层次分析法[10]中对决策矩阵中目标函数的重要性程度进行参数化为：

基于matlab对决策矩阵R求解特征解可得：

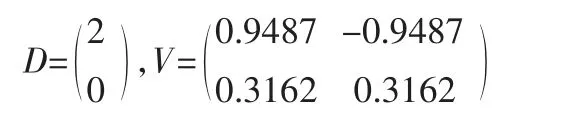
运用文献[10]中决策矩阵的一致性判别准则得到最大特征值对应的特征向量为：

依据特征向量w得到加权因子所占比为3：1，也符合式（8）的决策矩阵重要性参数的取值，最终可得静、模态目标函数的加权因子为0.75、0.25。

4.2 基于Dequation多目标函数定义

基于OptiStruct的多目标优化函数，在优化过程中因其局限性而只能进行单目标函数优化设计，尤其是在非凸优化问题中不能得到全部的Pareto解。运用Optistruct中的dequation函数定义面板并依据第2.2节的柔度最大值和最小值，第2.4节的一阶固有频率最大值和最小值并结合式（5）进行编辑可得：

式中：f（x，y）—多目标函数；x、y—多目标优化过程中的柔度和一阶固有频率。

5 多目标优化结果

对直齿轮的多目标拓扑优化以目标函数F（a，b）最小化，优化前后体积比为约束条件进行优化求解。通过35次得优化迭代得到齿轮结构的多目标优化结果、优化后的应力分布、柔度值和一阶模态振型，如图4～图5所示。

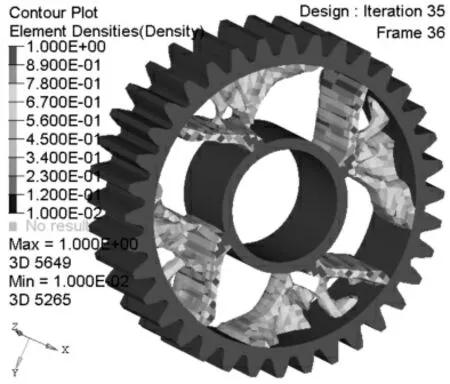
图4 直齿轮多目标拓扑结果Fig.4 Multi-Objective Topology Optimization Result of Gear

图5 直齿轮多目标优化后一阶模态振型Fig.5 First Order Modal Mode of Gear After Multi-Objective Optimization

优化迭代后直齿轮多目标拓扑优化后柔度值和一阶固有频率变化情况，如表4所示。

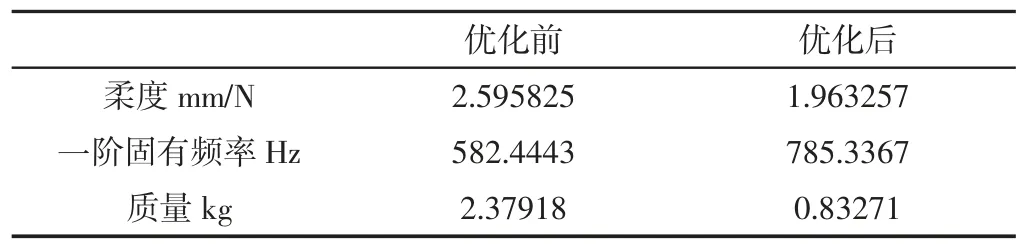
表4 多目标拓扑优化前后性能参数Tab.4 Performance Parameters Before and After Multi-Objective Optim ization

通过对齿轮多目标拓扑优化结果可得，齿轮柔度值从2.595825mm/N明显下降到1.748555mm/N，模态一阶固有频率从582.44Hz明显下降到785.40Hz，齿轮的整体质量从2.38kg下降到0.83kg，如表4所示。从图7中的一阶模态振型可以看出，齿轮受到绕Z轴扭转的趋势，表明实际工作过程中尽量避免给齿轮扭转激励，以免齿轮产生共振现象。

6 结论

对齿轮结构的优化设计主要引入拓扑学和多目标理论，运用OptiStruct对直齿轮进行多目标拓扑优化设计。基于OptiStruct对齿轮的多目标优化结果表明：齿轮柔度值得到明显的下降，即优化后齿轮提高了结果刚度，改善了结构力学性能；齿轮模态一阶频率地增大，大大地改善了结构的动态特性。基于层次分析法计算各子目标函数的权重比，为多目标优化目标的构建提供了理论依据。此外，还能为学者将更优的数理统计理论应用到优化技术中提供了一定的参考。