回传射线矩阵法在周期结构振动分析中的应用

陈 林，布英磊，叶 曦，王青山

（1.中国船舶及海洋工程设计研究院，上海200011；2.中南大学，机电工程学院，湖南 长沙 410083）

1 引言

周期结构是一种新型的复合周期材料，其特有的振动带隙特性在工程应用上具有较为实际的应用价值[1]。在周期结构分类方面，通常根据周期结构的周期维数进行划分，将周期结构划分为一维，二维和三维单元。因一维周期结构较为简单，虽然较二维，三维的研究较少，但是与工程应用领域较为贴合。目前，计算周期结构振动带隙的计算方法主要有[2]传递矩阵法，平面波展开法，集中质量法等，上述算法有着个各自的特点以及计算的领域范围。例如，传递矩阵法是一维周期结构的带隙特性计算中较为常见的计算方法，其计算量较小，但是较难处理二维，三维的周期结构模型[3]；平面波展开法是周期结构问题研究中较为常见的一种方法，将弹性模量等参数按照傅里叶级数进行展开，结合布鲁赫定理，将弹性波的波动方程转化为本征值进行求解，进而得到周期结构的能带结构[4]；集中质量法是利用离散化的物理思想，将集中质量引入到二维，三维周期结构带隙的计算过程之中[5]。上述三种方法均存在着较为明显的特点以及计算的领域范围。

对回传射线矩阵法的原理进行阐述，对其理论思想以及求解过程进行描述，并且给出以一维等截面周期结构对于轴向波的传输特性的计算作为算例。

2 算法原理阐述

回传射线矩阵法（MRRM）是1998年由Howard和Pao公开提出的，随着时代的进步和社会的发展，人们对回传射线矩阵法的研究逐渐深入，并且对其计算领域的范围逐渐进行深入的扩展研究[6]。近年来，随着对周期结构理论的逐渐研究，复合周期结构梁中弹性波的传输特性逐渐得到重视，引入回传射线矩阵法计算周期结构的振动特性曲线。

回传射线矩阵法基本思想是[7]：将整个结构划分为若干单元，在各个单元内建立对偶坐标系，以控制微分方程为基础，结合傅里叶变化，将时域范围内的偏微分方程转化为频域范围内的常微分方程，将弹性波的波动方程的解表达成简谐波的形式，根据在各个局域坐标内的出入关系，将简谐波设置成为入射波和出射波，将入射波的波幅和出射波的波幅作为未知量进行表达[8]。根据各自单元内物理量之间的关系得出相应的相位关系，根据节点处的力平衡方程和位移协调方程得出相应的散射关系，将各自节点的散射关系以及相位关系按照一定的关系进行组合排列，形成整体相位矩阵与散射矩阵，进而得到整体结构的回传矩阵，计算稳态响应，得出对应的频率响应函数曲线。

3 理论分析

3.1 单元划分与对偶变换

回传射线矩阵法是基于单元划分的思想，又因为一维周期结构是在x轴方向上周期排列的复合结构，二者共同拥有的单元划分思想为回传射线矩阵法的计算提供了较为便利的基础。

采用的局部坐标系是根据右手螺旋定则进行设定[9]。对于单元ij，引入两组对偶坐标系，如图1所示。分别定义为（x，y，z）ij和（x，y，z）ji，其中，（x，y，z）ij表示由由节点i沿着梁单元的轴线指向节点j的局部坐标，对应的，xij为由节点i到节点j的方向为正方向，则xji为节点j到节点i的方向为正方向。通过右手螺旋法则，可以得到相对应的yij和yji，zij和zji，可以看出yij和yji反向，zij和zji同向。同时定义，在对偶坐标系之中，xij=lij-xji。

图1 局部坐标定义Fig.1 Local Coordinate Systems for Beam Members

在上述定义的对偶坐标之中，可以确定在每个对偶坐标之中，轴向力N，剪切力Q，弯矩M等力向量以及轴向位移u，纵向位移v以及转角位移φ之间的关系，如式（1）所示。

对于单元ij而言，可以定义广义力向量Fij和广义位移向量Vij，二者的具体形式为：

因回传射线矩阵法的推导列式以及算法思想是在局部坐标系之中进行建立的，需要将局部坐标系之中的物理量转化为整体坐标系之中，因此需要进行对偶变换。对于单元ij内的广义力向量和广义位移向量而言，其对偶变换关系为：

式中：θ—局部坐标系中的x轴与整体坐标系中x轴的夹角；Fi

Oj，Vi

O

j

—整体坐标系下的广义力向量和广义位移向量。

3.2 相位关系矩阵

为了将波动方程解写成简谐波的形式，将简谐波定义为入射波和出射波，以单元12为例，入射波向量定义为：

对应的出射波向量定义为：

根据单元内的对偶关系，结合广义力向量与广义位移向量的简谐波形式，可以得出单元范围内的相位关系：

可以得到单一单元范围内的相位关系：

根据结构的节点定义，按照一定的排列顺序可以将单元相位关系矩阵组装成总体相位关系矩阵：

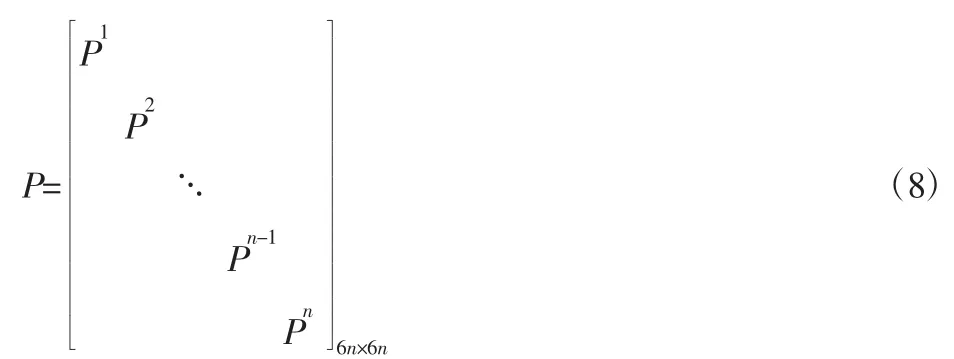
其中，P为6n×6n阶对角阵。通过节点的定义与单元的划分关系，可以得出总体结构的相位关系：

3.3 散射关系矩阵

回传射线矩阵法的散射关系矩阵是基于节点处的力平衡关系以及位移协调关系进行计算。假设节点i处有nj个单元，则作用在节点i出的外力与单元内力之间的力平衡关系表示如下：

式中：Tij—上述描述的转换矩阵；fi—作用在节点i处的外力源向量；Mi，Ki—节点i处的集中质量矩阵以及弹簧刚度矩阵。

结合广义力向量的简谐波形式，可以将上述力平衡公式写成：

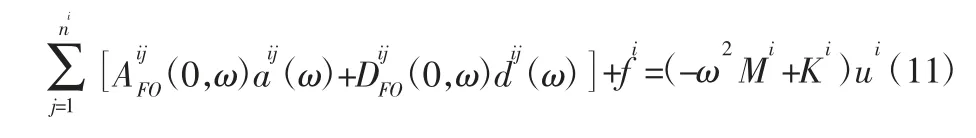
式中：Ai

Fj

O（x，ω），Di

Fj

O（x，ω）—6×6阶广义力传播矩阵，可以根据单元控制微分方程推到得出。

根据节点的位移协调条件，可以得出：

结合广义位移向量的简谐波形式，可以得出：

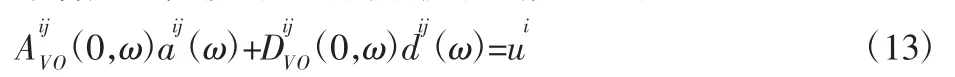
式中：Ai

Vj

O（0，ω），Di

Vj

O（0，ω）—6×6阶广义位移传播矩阵，可以对单元的控制微分方程进行推导得出。

根据上述力平衡关系矩阵以及位移协调关系矩阵，联立式（10）与式（11）消去位移向量ui可以得出节点i的散射关系：

式中：Si—局部关系散射矩阵；si—节点处的外力源向量，根据节点所受外力以及按照整个结构的节点排列顺序，可以得出整体结构的散射关系矩阵S：

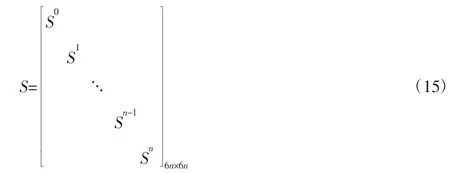
式中：S—6n×6n阶对角阵。通过节点与单元的划分定义，按照节点的排列顺序，则可以得到总体散射关系：

3.4 回传矩阵与稳态响应

为了将总体结构的关系矩阵进行组装，需要引入相位关系转换矩阵。我们可以了解到，出入波向量d和之间的具有相同的元素，但是二者之间各元素的排列顺序不同，因此需要引入转换矩阵U，可以得出：则有a=PUD

将上述总体相位关系矩阵以及散射关系矩阵进行联立，可以得出：

其中，定义R=SPU为系统的回传射线矩阵。

将相应的动力响应写成稳态响应的模式：

将相应的频率代入广义力与广义位移的表达式，可以得出时域范围内的额广义力与广义位移向量，如下所示，进而可以求出频率范围内的稳态响应，得出对应的频率响应函数曲线[6]。

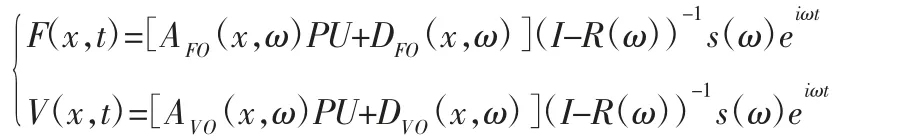
经过数据处理得出相应的频率响应函数曲线，研究分析其振动特性。

4 数值算例分析

本节基于Euler-Bernoulli梁理论，以一维等截面周期结构结构的稳态响应最为算例进行计算，本节采取三周期的一维等截面周期结构模型，如图2所示。周期结构晶格，如图3所示。具体参数如下：铝：密度ρ1=2799kg/m3，泊松比υ1=0.33，弹性模量E1=7.21×1010。有机玻璃：密度ρ2=1142kg/m3，泊松比υ2=0.36，弹性模量E1=0.32×1010。结构物理参数：l1=l2=50mm，横截面为圆形r1=r2=2mm定义晶格常数N=l1+l2=100mm，组分u=l1/（l1+l2）。

图2 周期结构模型Fig.2 Structure of Periodic Structures Beam

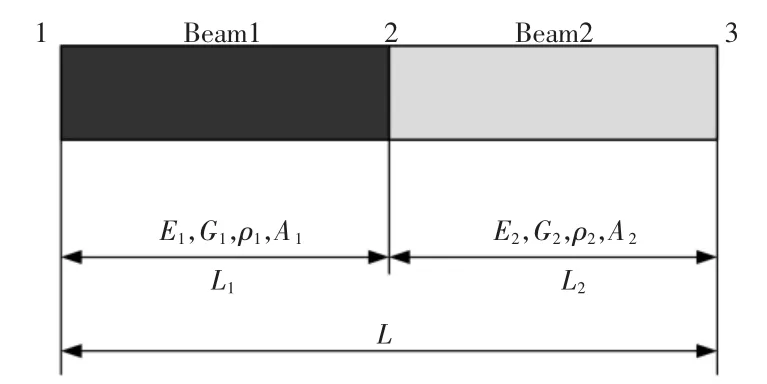
图3 晶格简图Fig.3 The Schematic of the Unit Cell

基于回传射线矩阵法的单元划分思想，将一维等截面周期结构模型按照节点与单元的思想进行划分，得到的节点定义与单元划分，如图4所示。

图4 单元与节点定义Fig.4 The Definition of Unit and Node

在每一段梁单元之中建立对偶坐标系，以梁单元12以及单元23之中为例进行建立，得到的对偶坐标系，如图5所示。

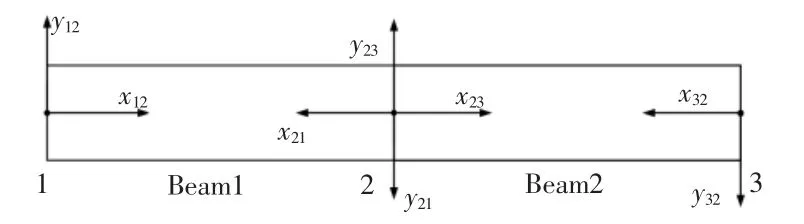
图5 对偶坐标建立Fig.5 The Establish of Dual Coordinate

基于Euler-Bernoulli梁理论，推导单元的控制微分方程，得出控制微分方程的解，并且写成简谐波的形式，得出对应的广义力向量与广义位移向量：

通过前文所述的结构的相位关系，将每个梁单元之中的物理量进行相应的对偶变换，可以得出单元的相位关系矩阵，按照节点的定义顺序，将节点1至节点6的单元相位关系矩阵进行组装，得出总体结构的相位关系矩阵，其中P1-6为6×6阶矩阵

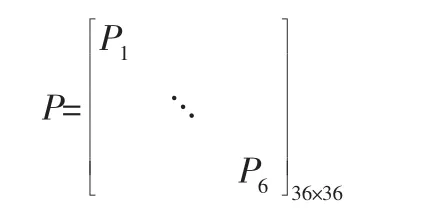
通过各个节点处的力平衡关系以及位移协调关系，得到整体结构中各个节点的散射关系矩阵，其中，节点0与节点7的散射矩阵为3×3阶，其余散射矩阵为6×6阶矩阵。

通过引入转换关系矩阵U，转换矩阵U的特点为：其每一行以及每一列有且仅有一个元素为1，其余元素为零，并且其逆矩阵为其自身。

对于整个结构，通过引入边界条件，得出总体结构对应的回传射线矩阵，求解相应的稳态响应，得出对应频率范围内的振动特性曲线。

本节算例之中，为了减小与理想周期结构结构之间的差距，采取自由边界条件进行计算[10]，取一维等截面周期结构的左端面为激励输入端，取右端面为激励响应拾取端；本节算例施加简谐位移轴向激励，其振幅为1mm。

为了验证本节算例计算一维等截面周期结构对轴向波的频率响应函数曲线的正确性，因此采取有限元分析法对上述算例进行有限元分析计算[11]。

采用AnsysWorkbench进行有限元分析，具体设置参数如下：

材料参数与周期结构物理参数：与前文结构描述相同。

网格划分：因模型较为基本，且较为简单，因此采用自由网格划分的方法，定义六面体单元的基本尺寸为2mm。

施加载荷：施加轴向简谐位移载荷，位移的幅值为1mm，激振频率范围为（0～40）kHz。

分析参数设置：因施加的载荷为简谐位移载荷，采用谐响应分析模块，采用完全算法，即：Full算法。

图6 有限元分析示意图Fig.6 The Schematic of Finite Element Analysis

为了比较分析研究本节算例的数值计算结果以及有限元分析方法之间的关系，由图7可以看出，由有限元分析方法计算得出的曲线与由回传射线矩阵法计算得出的频率响应函数曲线基本保持吻合，因此可以证明回传射线矩阵法计算一维等截面周期结构对于轴向波的频率响应函数曲线的正确性。

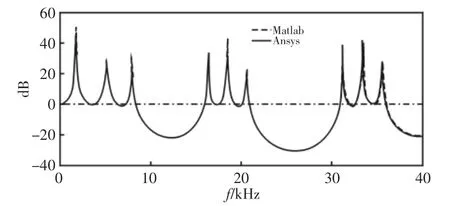
图7 有限元与数值计算对比Fig7 The Comparison of FEM and Numerical

5 结论

依据回传射线矩阵法的理论思想，依据其单元划分以及节点定义思想，结合单元的相位关系矩阵以及节点的散射关系矩阵，通过引入转换矩阵以及总体关系矩阵的组装，结合边界条件，得出总体结构的回传射线矩阵，求得结构中的稳态响应，得出频率范围内的振动特性曲线。以一维等截面周期结构结构对与轴向波的传输特性曲线进行了计算，并且与有限元分析方法进行了对比，证明回传射线矩阵法对周期结构结构振动特性计算的正确性。