绳驱动刚柔混合式波浪运动补偿机构的运动学建模与碰撞干涉检测
王立栋, 陈原
(山东大学(威海) 机电与信息工程学院, 山东 威海 264209)
0 引言
当两船间进行集装箱货物转运时,为避免吊装集装箱与被补给船甲板之间发生不必要的碰撞,确保吊装作业的安全,同时实现集装箱准确下放至被补给船甲板的指定位置,需要在吊装作业过程中利用波浪补偿装置消除补给船与被补给船之间的相对运动。由于海上无规则的波浪和海风运动,海洋作业平台或者工作船舶在进行海上作业时会产生不规则运动,需要进行多维相对运动补偿。多维相对运动补偿技术又称为波浪运动补偿技术,已广泛应用于海上石油开采[1]、浮吊重载打捞[2]、船舶间货物转运[3]、深海采矿[4-5]、船舶建设[6]、潜水器吊放回收[7]、深海勘察[8]等海上作业领域。近年来,随着海洋重工业的高速发展,提高海上作业精度逐渐成为海上作业顺利进行的主要因素。海上波浪运动补偿装置的研制,可以大大提高海上吊装作业的精度和稳定性,对提高港口吞吐能力具有一定的促进作用。
现有用于海上吊装作业的波浪运动补偿技术,大多采用单根驱动绳直接吊装货物,同时结合复杂的电、液或者气动控制系统实现货物在升沉方向上的相对运动补偿,该补偿技术也称为主动或者被动式升沉补偿技术[9]。随动小车补偿系统[10]和升沉补偿缓冲器[10]是常用的被动式升沉补偿系统。当进行货物吊装作业的两船发生相对升沉运动时,起重机驱动绳索承受的张力值会发生变化,此时波浪运动补偿器会根据张力值的变化对补偿参数进行调整,从而达到被动式波浪补偿的目的。但是,被动补偿系统具有滞后性和补偿精度较低等缺点。而主动式波浪补偿系统中的主动控制器能实时检测两船之间的相对运动偏差,并能利用先进的控制算法或者结合波浪预报系统有效地提高补偿精度。然而,主动式补偿方式大多结合液压绞车和电动吊臂等复杂系统。这类补偿方式具有补偿效率低和消耗能量多等不足。与多维波浪运动补偿技术相比,升沉补偿技术的功能单一,仅仅可以实现升沉方向的相对运动补偿,货物的放置位置精度和稳定性难以得到保证。
为了弥补传统升沉补偿技术的不足,国内外学者开展了多自由度相对补偿技术的研究。20世纪80年代美国国家标准与技术研究院研制出一种用于重物吊装的绳驱动并联机器人RoboCrane[11],其中6根驱动绳之间按照Stewart构型连接,该机构能够控制货物实现6自由度运动。美国海军研究办公室研制出用于海上波浪补偿的LVI LO/LO起重机[12],可通过8根冗余驱动绳控制货物实现6自由度运动,同时也能利用惯性测量单元和摄像机阵列测量船与船之间的相对运动,是目前国际上最先进的6自由度波浪运动补偿技术。Lü等[13]也提出了与LVI LO/LO相似的6自由度并联波浪补偿系统,并完成了相关理论分析和相应实验平台的搭建,验证了该技术用于海上波浪补偿的有效性。但是,该类补偿装置为全柔性绳索驱动机构,会导致机构整体刚度减小,抗干扰性能和稳定性较刚性机构差,易受海风等外部复杂环境的干扰。此外,Kim等[14]也开展了6自由度补偿技术的研究,利用双层天车、张力控制器和智能移动平台等机构来控制被吊装货物实时调整位姿状态。但是,该补偿系统直接与集装箱货物相连的提升模块为两根驱动绳驱动的被动式升沉补偿系统,补偿精度相对较低。Wang等[15]开发了一种可以实现3自由度波浪运动补偿功能的海上起重机,该补偿装置由一个2自由度刚性并联抗摆平台和一根在升沉方向牵引货物的驱动绳组成。顾永凤等[16]利用3自由度全刚性并联机构开发了一种用于船上的波浪补偿运动平台,可补偿横摇、纵摇、垂荡3个方向的波浪运动。但是,相对于绳驱动并联机构,纯刚性并联机构的有效工作空间较小,且只能通过改变整体机构的大小来满足较大的波浪运动补偿,具有消耗能量较多和惯性较大等缺点。综上所述,传统多维波浪运动补偿技术大都通过纯柔性绳驱动并联机构和纯刚性并联机构来实现波浪补偿,然而纯柔性绳驱动并联机构的抗干扰性能和稳定性较差,纯刚性并联机构的有效补偿工作空间较小和能量消耗较大。如果能充分运用绳驱动和刚性并联机构之间的各自优点,则波浪补偿装置就能更加有效地补偿两船之间的相对运动。
近年来,绳驱动并联机构凭借其结构简单、整体惯性小、有效工作空间大等优点得到飞速发展,并已得到广泛应用。比较有名的绳驱动并联机构有Robocrane[17]、FALCON-7[18]、SEGESTA[19]、IPAnema[20]等。另外,加拿大滑铁卢大学成功研制出两种刚柔混和式超高速并联机构BetaBOT[21]和DeltaBot[22]。BetaBOT由3对两两平行的驱动绳和1根中间刚性驱动支链组成,3个驱动电机驱动的摇臂分别驱动3对驱动绳,可实现3个平动自由度,DeltaBot机构与BetaBOT机构相似,但3对相互平行的驱动绳分别由3个电机驱动,也可以实现3个平动自由度,但遗憾的是这两种机构均无法实现3个转动方向上的运动。加拿大女王大学机器人实验室研制出一种刚柔混合式并联机构CAT4[23],利用6根驱动绳实现3转动和1移动的4自由度运动,该机构已经用于执行太空的探索任务,但是该机构无法实现在升沉方向上的运动。Alamdari等[24]设计了一种刚柔混合式康复机器人系统,主要用于增强功能性肌肉骨骼恢复和神经受损康复的辅助运动疗法。众多国内外学者还将刚柔混合式并联机构应用于仿造人体眼球[25-26],仿制拟人手臂[27-28]、腿机构[29]以及肩关节[30]等仿生运动中。这些仿生机构中的驱动绳和中间支链分别模拟人体肌肉和骨骼,中间刚性支链可以实现对驱动绳的支撑作用,使驱动绳时刻保持张紧状态。但是,上述刚柔混合式并联机构中的中间刚性支链长度不可控,从而导致其工作空间有限且灵活性较差,很难应用到海洋环境下的6自由度全方位波浪运动补偿。结合纯柔性绳驱动和纯刚性并联机构的各自优点,本文提出一种用于海上波浪运动补偿的6自由度绳驱动刚柔混合式并联机构。该刚柔混合式并联补偿机构可以看成是多根柔性驱动绳和刚性主动驱动支链混合驱动来实现海上波浪运动的补偿,该绳驱动刚柔混合式并联机构不仅有效空间大,而且刚度也较大。
为了实现海上6自由度波浪运动补偿功能、提高海上作业精度和稳定性,本文构思了一种多维方向的波浪运动补偿技术,提出一种用于海上波浪运动补偿的绳驱动刚柔混合式并联机构。首先,分析绳驱动刚柔混合式波浪补偿机构装置的功能需求。其次,计算机构的位姿逆解和驱动绳与中间支链上的速度变化,建立机构的雅克比矩阵。再次,建立机构的静力学模型,计算柔性驱动绳和刚性支链上的张紧力分配大小。然后,对整体机构各部件的位置利用几何法进行碰撞分析检测。最后,通过仿真分析验证该机构用于海上波浪运动补偿的可行性。
1 海上波浪运动特点与波浪补偿思想
对于海上作业,海洋状况是影响海上吊装作业的精度和稳定性一个重要影响因素。海平面的不规则运动使得海上作业船会产生横荡、纵荡、升沉、横摇、纵摇和艏摇6自由度运动,如图1(a)所示。在波浪运动的作用下,货船船甲板会在6个自由度方向分别产生不同程度的波动变化。为了避免集装箱与船甲板之间发生碰撞,同时保证货物准确地下放到指定位置,需要利用波浪补偿技术使集装箱位姿实时与船甲板指定放置位置的位态保持一致,以保证集装箱的精准安全吊装工作,如图1(a)所示。
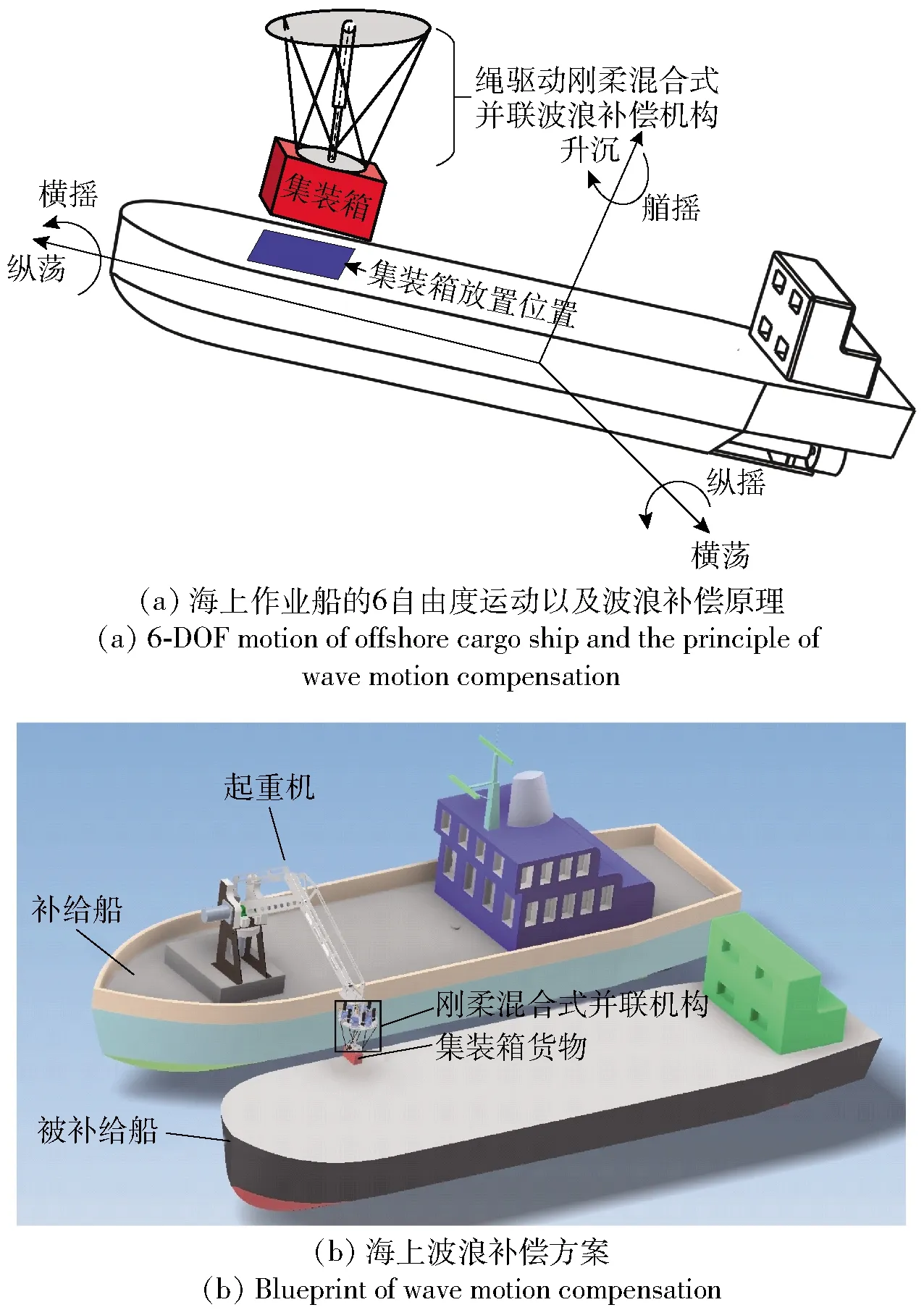
图1 海上波浪补偿原理及方案图Fig.1 Principle and blueprint of wave motion compensation
统计数据[31]显示,要使集装箱运输船的海上吊装作业效率达到90%~100%,作业货船在纵荡、横荡和升沉方向上的运动必须在以下范围内:±(0.6~1.0 m)、±(0.6~0.8 m)和±(0.6~0.9 m),而在横摇、纵摇和艏摇方向上的运动角度必须满足以下范围:±3.0°、±1.5°和±0.5°. 但是,海洋状况的复杂不确定性很难保证海面环境随时都满足上述海况。据统计,海洋表面85%的时间内都处于3~6级海况中,波浪高度能达到5.18 m,横摇角和艏摇角分别能达到19°和8°[32]. 因此,亟需设计一种多维波浪运动补偿装置,使其作业效率达到90%~100%,以提高海上吊装作业精度和作业效率。在进行海上吊装作业的过程中,通过重型起重机将集装箱货物吊至待放置区域上方区域,如图1(a)所示。利用传感器反馈实时货物位姿与待放置区域位姿之间的差距,然后由刚柔混合式波浪补偿装置对集装箱货物在6自由度方向不断微调,直至实现与待放置区域位姿完全重合,实现6自由度波浪补偿的功能,如图1(b)所示。在补偿装置内部通过6根驱动绳和1根刚性支链实现运动平台以及被吊集装箱货物的6自由度运动。这一过程仅仅通过补偿装置内的电机实现波浪补偿功能,具有消耗能量小、补偿精度高等优点。
2 绳驱动刚柔混合式波浪补偿机构的运动学模型
2.1 绳驱动刚柔混合式波浪补偿机构的位置模型
滑铁卢大学实验室曾开发一套如图2(a)所示BetaBot刚柔混合式并联机构,该机构利用3对相互平行的驱动绳和1根中间刚性支链驱动运动平台实现3个平移方向的自由度运动[21]。为了进一步实现更多自由度,满足海上多维波浪补偿运动的需求,本文将BetaBot驱动绳的配置进行改进,使6根驱动绳按照参考文献[11]中的Robocrane配置方式进行配置,提出一种如图2(b)所示用于海上多维运动波浪补偿的6自由度绳驱动刚柔混合式波浪补偿机构。安装于静平台上的6个驱动电机分别驱动6根绳,6根驱动绳上下铰接点成3-3配置,同时在两平台之间并联1条UPS主动驱动刚性支链。运动平台通过6根驱动绳和1条UPS中间刚性支链,可以实现空间6自由度的运动。因此,与BetaBot机构相比,本文所提6自由度绳驱动刚柔混合式波浪补偿机构不仅能扩展BetaBot机构的自由度,而且可以有效地改善整体机构的刚性和提高机构的承载力[33-34]。
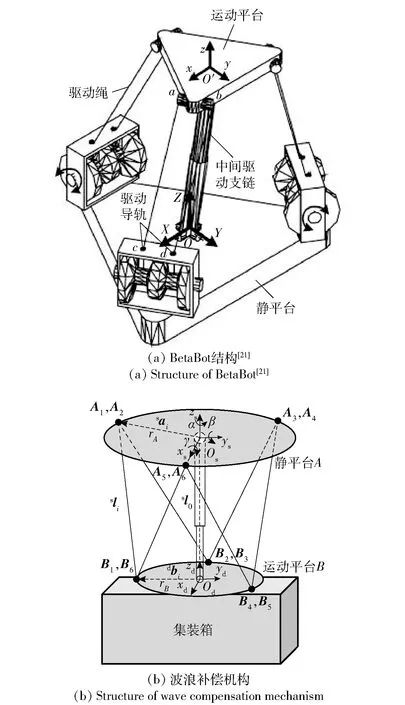
图2 滑铁卢大学实验室开发的BetaBot刚柔混合式并联机构[21]和本文提出的绳驱动刚柔混合式并联机构Fig.2 BetaBot rigid-flexible hybrid driven parallel mechanism[21] developed by the University of Waterloo Laboratory and the proposed rigid-flexible hybrid driven wave compensation mechanism
如图2(b)所示为绳驱动刚柔混合式并联机构简图与坐标轴,其中A为静平台,B为动平台,动平台直接与集装箱平台相连。为了简化机构分析,假定地球坐标系Osxsyszs位于静平台的质心处,运动坐标系Odxdydzd位于动平台的质心处。图2(b)中:α、β和γ分别为绕zs轴、ys轴和xs轴转动的角度;sli为沿第i根绳的矢量,sl0=OsOd为沿中间刚性支链的矢量;Ai与Bi分别表示驱动绳与静平台和动平台的铰接点坐标,i=1,2,…,6;sai和dbi分别为沿静平台和动平台半径方向的矢量,sai=OsAi,dbi=OdBi,其欧几里得范数大小为相应平台的半径;rA和rB分别表示静平台和运动平台半径。
静平台A和动平台B之间通过6根驱动绳和1根中间刚性支链连接。运动坐标系{Odxdydzd}相对于地球坐标系{Osxsyszs}的姿态变换矩阵选用zs-ys-xs欧拉角表示,相应的变换矩阵为
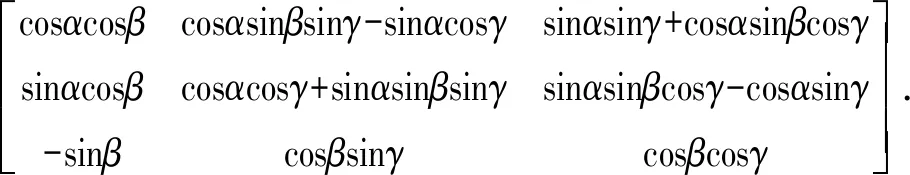
由矢量封闭原理,可得
sli=sOd+sRd·dbi-sai.
(1)
由(1)式可以得出该机构的逆运动学模型:
(2)
2.2 绳驱动刚柔混合式并联补偿机构的雅克比矩阵
机构雅克比矩阵对进一步分析机构静力学、刚度、工作空间以及奇异性具有重要的意义[35]。将(2)式的逆运动学模型两端同时对时间t求导数,由于sai和dbi均为定值,应用线性代数恒等式cTd+dTc=2cTd=2dTc并化简,可得
(3)
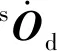
(4)
式中:sΩd为运动平台B相对于静平台A的角速度叉积算子,
ωx、ωy和ωz分别表示动平台绕各个坐标轴的角速度分量,sωd表示运动平台和角速度。
结合矢量混合积运算法则,(3)式可进一步转换为
(5)
(5)式的矩阵形式表示为
(6)
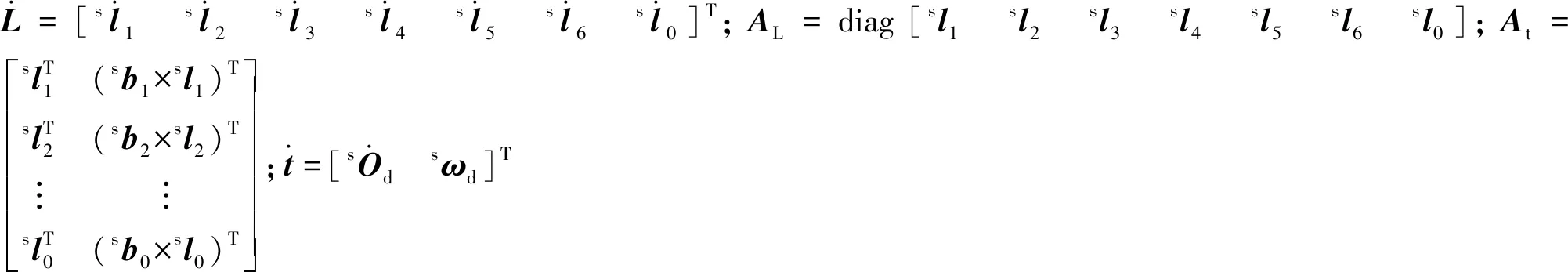
(7)
2.3 速度和加速度模型
由(5)式可知,运动平台的线速度和角速度映射到第i根驱动绳上的速度可以表示为
(8)
(8)式两边同时对时间t求导,可得机构第i根驱动绳的加速度:
(9)
由(9)式可以求得驱动绳与中间支链的加速度随运动平台运动的变化规律。
3 驱动绳张紧力的计算与分配
相比于传统的刚性并联机构,绳驱动并联机构由于柔性驱动绳本身具有单向受力特点(只能承受拉力,不能承受压力)[36]。当运动平台处在任意位姿状态时,无法确定机构整体是否达到静力平衡状态,这也是整体机构能否完全发挥其优良性能的关键所在。静力学分析对于进一步计算每条驱动支链上的张紧力起着重要作用。
在集装箱吊装作业过程中,集装箱货物的质量相对于整体补偿装置较大,在分析中不能忽略,因此将被吊装货物的质量等价替换成一根拉力大小恒定、方向始终沿着重力方向的驱动绳支链。机构中间的主动刚性UPS支链既可以承受拉力,又可以承受压力。为了简化机构整体的静力学分析,将中间刚性支链当成两条沿着刚性支链同时方向相反,并时刻处于张紧状态的驱动绳。当刚性支链受到拉力作用时,其方向由动平台中心点Od指向静平台中心点Os(即沿OdOs方向);当刚性支链受到压力作用时,其方向由静平台的中心点Os指向动平台的中心点Od(即沿OsOd方向)。机构整体静力学模型如图3所示。
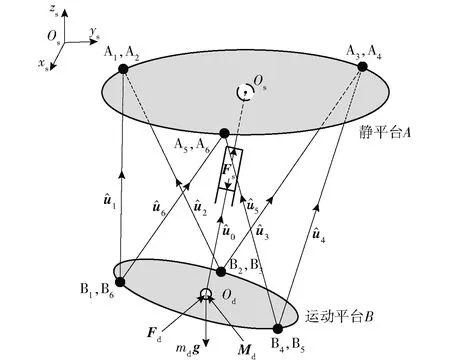
图3 静力学模型图Fig.3 Statics model
图3中,fi为驱动绳支链所受的张紧力大小,Fs为中间刚性支链所受的力,mdg为动平台及重物的重力总和,(Fd,Md)表示海风等外力作用于运动平台B上的任意力旋量。
在某时刻静止状态时,所有驱动绳和中间刚性支链所受到的内力、海风作用于运动平台B上任意的力旋量(Fd,Md)等外部力旋量,以及运动平台上的重力必须达到静力平衡状态。结合作用于运动平台上的力和力矩平衡方程[36],可得
(10)
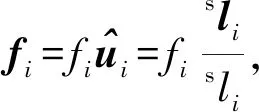
等式fi代入(10)式,可得
Ac×f+Ab×f0+Mdg+Wd=0,
(11)
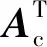
将吊装和连接于运动平台上的集装箱重力和中间刚性支链分别等价替换成驱动绳模型,可以将(11)式进一步写成该绳驱动刚柔混合式并联机构的整体静力平衡方程:
(12)
式中:AT表示将运动平台及重物视为额外驱动绳后整体机构的雅克比矩阵;ftot表示将运动平台及重物的重力和视为额外驱动绳后整体机构张紧力所组成的力矩
为了控制完全约束或冗余约束绳驱动并联机构的动平台沿着任意给定运动轨迹运动,需要实时计算机构中每根驱动绳的张紧力大小(即每根驱动绳所分配到的张紧力大小)。尤其当动平台在以较高速度或较高加速度运动时,绳的松弛会使动平台产生晃动现象,对于机构发挥其补偿性能显然是不利的。为了避免绳出现松弛现象,同时也为了限制绳的受力超过极限值,对驱动绳受力分配和受力优化是非常必要的。
由(12)式可得外部任意力旋量Wd和驱动绳以及中间刚性支链上的受力fall之间的关系为
ATfall+Wd=0.
(13)
如果利用p-范数(p>1)将计算绳所受张紧力大小的问题转化为计算最优解问题,即将(12)式转换为如(14)式的最优化问题,则可以找到具有连续力分布的轨迹[36]:
(14)
式中:m为驱动支链的数量。
根据Verhoeven定理[36],当范数p>1时,(14)式具有多维解空间,即求得的张紧力大小没有唯一解。为了解决这一复杂问题,众多学者提出了多种方法求解最优解[37-40]。本文利用代数变换中的欧几里得范数(p=2)结合伪逆矩阵A†T,将驱动绳上所受张紧力大小表达为如下封闭解形式[41]:
(15)

与其他方法相比,力封闭解算法仅利用矩阵转置和矩阵基本运算求解伪逆矩阵,计算简单且速度快,可以有效缩短计算时间[41],可用于实时控制,同时可以根据伪逆矩阵A†T中的(ATA)-1存在与否来判断机构是否位于可行工作区间内[41]。
4 碰撞干涉检测
波浪补偿机构可能会发生驱动绳与驱动绳之间的碰撞干涉、驱动绳与中间刚性支链之间的碰撞干涉,以及驱动绳与运动平台(货物)之间的碰撞干涉。当绳驱动刚柔混合式并联机构的驱动绳、中间刚性支链以及动平台之间发生碰撞或者干涉时,绳驱动刚柔混合式并联机构在运动过程中会失去本身的灵活性和稳定性,严重时会损坏机构本身,对于机构的设计分析显然是不允许的。同时,碰撞干涉现象也会影响机构整体工作区间的大小。因此在机构分析过程中,碰撞检测是必要的也是重要的一步。
4.1 驱动绳之间的碰撞干涉检测
本文采用几何矢量方法检测驱动绳之间是否发生碰撞干涉,即将两条驱动绳看成两个矢量,通过计算矢量之间的最小距离判断驱动绳之间是否发生干涉现象。驱动绳之间碰撞干涉检测示意图如图4所示。图4中:d为两根驱动绳之间的距离;li和lj分别为第i、第j根驱动绳的长度,li=AiBi,lj=AjBj.
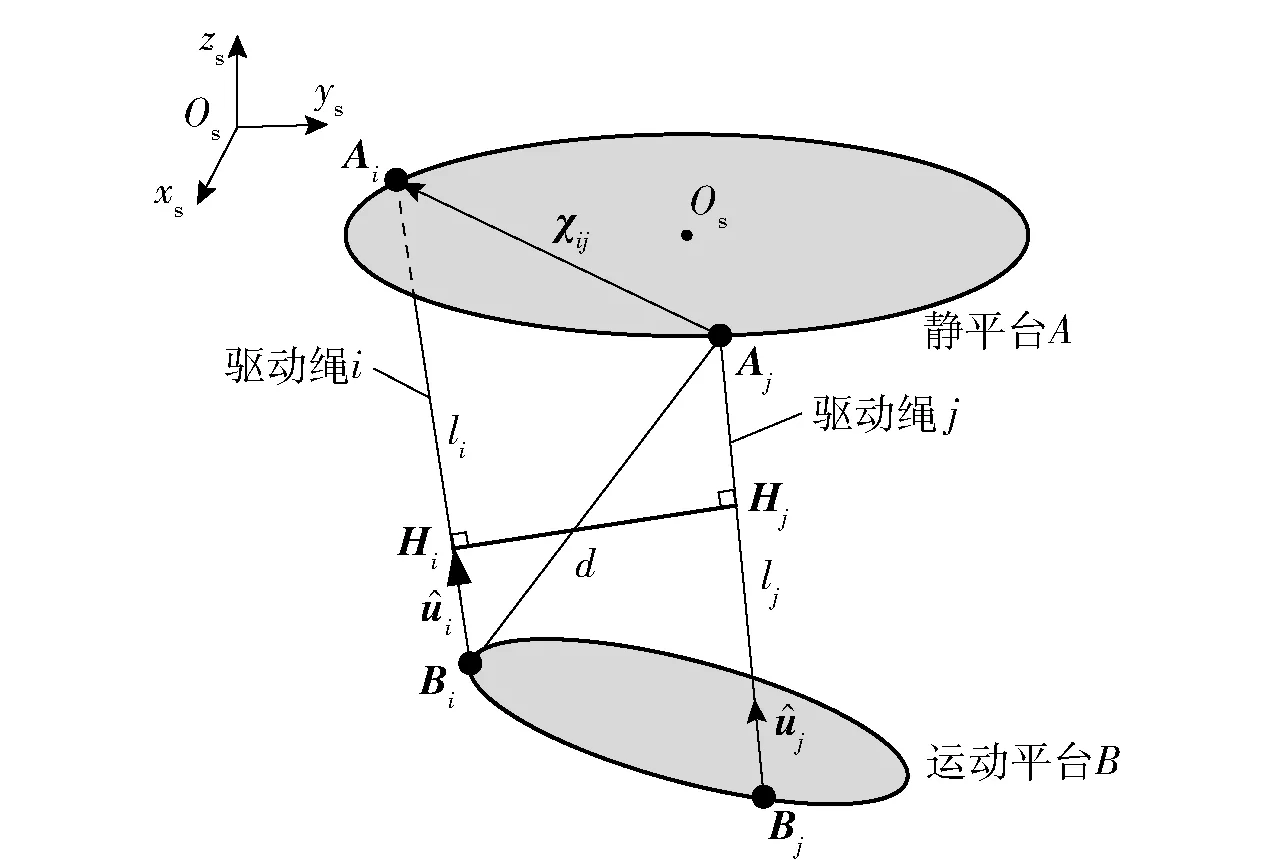
图4 驱动绳之间碰撞干涉检测示意图Fig.4 Schematic diagram of collision interference detection of driving cables
由图4可以看出,任意两条驱动绳i和j之间存在点Hi和Hj,使得点Hj到驱动绳j的距离最短,点Hj到驱动绳j的距离最短可以表达为d=(AiBi,AjBj)=mind(Hi,Hj),{Hi∈AiBi,Hj∈AjBj},d(·)表示两根驱动绳之间的距离。当‖HiHj‖<2σ时,可以判断两根驱动绳之间发生碰撞干涉,其中σ表示垂直于驱动绳横截面的半径。进一步,点Hi和Hj在空间坐标系下可以表示为
OsHi=sai-cii,OsHj=saj-cjj,
式中:ci和cj为任意大小的实数;i和j分别表示沿第i、第j根驱动绳方向的单位矢量。此时令向量χij=Ai-Aj,由图4可得重心坐标系下的垂直向量为
(16)
如果两向量AiBi和AjBj相关,则系数ci和cj分别存在唯一的值。当(16)式中的两个方程线性独立时,意味着线段是平行的,在这种情况下,ci=0或cj=0为方程组的解。如果ci或cj不满足0 由图4可以看出,驱动绳与动平台的铰接点为两根相邻驱动绳共用一个铰接点,此时相邻两根驱动绳之间的最短距离d为0 mm,故由以上分析可知相邻驱动绳碰撞干涉的现象不会发生。进一步通过计算可以判断非相邻驱动绳之间的碰撞干涉现象是否发生。 可以将中间刚性支链视为大直径驱动绳,从而驱动绳与中间刚性支链之间的碰撞干涉检测方法与4.1节中两条驱动绳之间的碰撞干涉检测类似。此时,判断条件变为‖H0Hi‖<σ′+σ,其中H0表示中间刚性支链上到驱动绳li距离最短的点,σ′表示中间刚性支链的半径大小。因此可以通过判断c0和ci的大小,来检测中间刚性支链与驱动绳之间是否发生碰撞干涉。 由于在驱动绳与运动平台的连接配置上,相邻两根驱动绳共用一个与运动平台相连的铰接点,这些铰接点在运动平台上的位置呈三角形。因此,可以通过检测驱动绳所在的直线与运动平台上铰接点组成的三角形平面之间的位置关系,来判断驱动绳与中间刚性支链之间是否发生碰撞干涉(见图5)。 图5 驱动绳与中间刚性支链之间碰撞干涉检测示意图Fig.5 Schematic diagram of detecting the collision interference between the driving cables and central rigid branched chains 由图5可知,驱动绳li所在直线可以表示为sli=Bi+cki,ck为任意大小的实数,运动平台上3个铰接点Bi、Bj、Bk组成一个位于运动平台内的三角形平面。令Q0=Bj-Bi且Q1=Bk-Bi,则三角形平面内的单位长度法线向量可以表示为 (17) 为了模拟绳驱动刚柔混合式并联机构在地球坐标系Osxsyszs下的补偿运动,设定动平台的平动轨迹分别为 (18) 同时,为了模拟补偿在横摇、纵摇、艏摇3个欧拉角方向上货物与被补给船之间的相对转动,设定动平台在转动方向上的运动轨迹分别为 (19) 假定平动补偿轨迹从位置点P1=(0 mm,0 mm,-600 mm)开始计时,补偿位置终点为P2=(0 mm,0 mm,-600 mm),补偿时间T=8.0 s,补偿两个运动周期,设计的补偿机构其他结构参数为 根据(2)式逆运动学方程,结合模拟轨迹方程(18)式和(19)式,利用MATLAB软件计算得到补偿过程中驱动绳以及中间支链的长度变化,仿真结果如图6(a)所示;进一步分析(8)式和(9)式,可得关于驱动绳以及中间支链的速度和加速度变化趋势,如图7(a)、8(a)所示;进一步在ADAMS仿真软件中利用Cable模块搭建补偿机构的物理模型,仿真得出驱动绳及中间支链的长度、速度以及加速度的变化曲线,如图6(b)、图7(b)和8(b)所示。以上仿真结果均表明在补偿过程中,驱动绳以及中间支链的长度、速度和加速度变化连续平滑,且变化均在可控范围内。通过对比分析可知各变化趋势基本一致,同时MATLAB软件理论计算结果与ADAMS软件仿真结果最大误差在5%以内,证明了所建数学模型的正确性,为后期驱动绳张紧力的计算分析提供了基础。 图6 驱动绳及中间支链长度变化Fig.6 Length variation of cables and central rigid branched chain 图7 驱动绳及中间支链速度变化Fig.7 Velocity variation of driving cables and central rigid branched chain 图8 驱动绳及中间支链加速度变化Fig.8 Acceleration variation of driving cables and central rigid branched chain 图9 波浪补偿实验样机Fig.9 Experimental prototype of wave motion compensation system 根据(15)式,假定驱动绳最小拉力值fi,min=3 N,最大极限拉力值为fi,max=100 N,货物集装箱负载mdg=80 N,外部力旋量取特例Wd=0简化计算。通过MATLAB软件进行仿真分析,得到驱动绳以及中间支链所受张紧力及拉压力理论计算值,MATLAB软件仿真理论值如图10所示。 为了保证补偿过程的顺利进行,需要实时检测波浪补偿装置自身机构内部各部件间是否发生碰撞干涉。通过第4节的理论分析和5.1节的结构参数设定,利用MATLAB软件数值仿真计算和ADAMS软件模拟仿真,在模拟补偿波浪运动过程中均未发生部件间的碰撞干涉现象,验证了该补偿装置在进行波浪补偿过程中的可行性,保证了机构在波浪补偿过程中的安全、可靠性。 通过搭建如图9所示1∶20等比例绳驱动刚柔混合式波浪补偿实验平台,所搭建的实验平台主要由计算机控制端、UMAC运动控制卡、6根驱动绳及其对应的驱动模块、中间刚性支链、AML拉压传感器以及拉压力数据采集模块组成。利用AML拉压传感器实时检测补偿过程中驱动绳以及中间刚性支链所受张紧力的大小,并在8 s的运动周期中提取100个拉力样本数据值,各驱动绳与中间支链所受张紧力的理论计算值和实验值对比如图10所示。由图10可见,各驱动绳和中间支链的理论计算值与实验值变化趋势大体一致且呈周期性变化,变化较为平滑。其中驱动绳所受张紧力大小均在可控范围内,二者最大误差在25%以内,验证了该算法的有效性。由于在理论分析中没有考虑驱动绳与线轮之间摩擦力以及外部力旋量等其他外部影响因素,导致实验值与理论值存在一定的误差。 通过搭建如图11所示模拟波浪运动补偿平台,利用造浪装置和船模分别模拟海上波浪运动以及被补给船。由图11(a)、图11(b)和图11(c)可以看出,吊装有集装箱的波浪运动补偿平台能实现实时补偿模拟的波浪运动,具有明显的波浪补偿效果;由图11(d)可以看出,被吊集装箱整体基本放置在被补给船甲板的指定位置处。综上所述,模拟实验分析验证了该创新设计的多维波浪补偿装置的有效性和可行性。 本文针对海上多维波浪运动补偿,创新设计了一种6自由度绳驱动刚柔混合式波浪补偿机构,该波浪补偿机构解决了现有海上波浪补偿功能单一的问题,实现了多维波浪运动补偿的功能。通过理论仿真与实验分析得到如下结论: 图10 驱动绳与中间支链张紧力变化Fig.10 Tension distributions on the driving cables and the center branched chain 图11 多维波浪运动补偿效果图Fig.11 Effect pictures of multidimensional wave motion compensation 1)补偿机构在给定的6自由度运动轨迹下,驱动绳以及中间支链的长度、速度以及加速度变化均是平滑连续的,且数值变化都在合理范围内,并与ADAMS软件模型仿真结果进行了对比,验证了该机构数学模型的正确性,同时仿真对比结果也表明了该波浪补偿机构在波浪补偿过程中的平稳、连续性。 2)基于构建的整体静力学模型,利用力封闭算法计算了驱动绳和中间刚性支链上的张紧力分配大小;对波浪补偿过程中驱动绳及中间刚性支链所受张紧力大小进行了数值仿真和实验验证,其仿真和实验结果间的误差在合理范围内,验证了该算法的有效性,为下一步对算法的优化和张力控制提供了基础。 3)通过对机构中各个运动部件之间进行碰撞干涉的数值仿真分析,验证了该机构各部件之间在波浪补偿运动过程中没有出现碰撞干涉现象,保证了机构在波浪补偿过程中的安全、可靠性。 4)通过搭建实验模拟平台,模拟波浪运动补偿,验证了本文创新设计的多维波浪运动补偿装置的有效性和可行性,为今后的实际应用奠定了基础。4.2 驱动绳与中间刚性支链之间的碰撞干涉检测
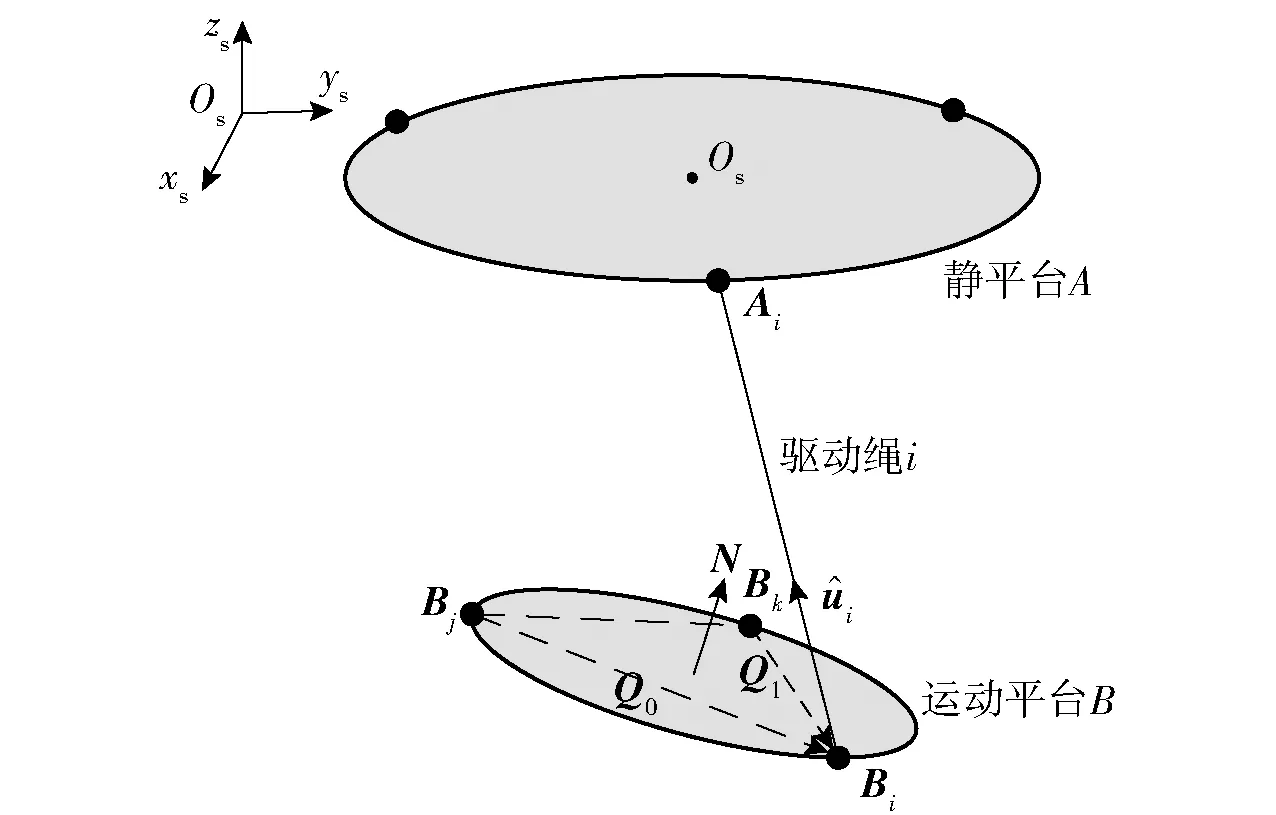
4.3 驱动绳与运动平台之间的碰撞干涉检测
5 数值算例与实验分析

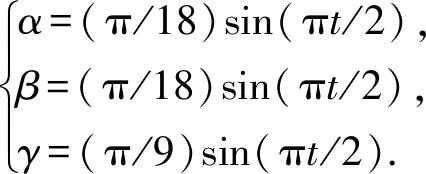

5.1 绳长及中间支链长度、速度以及加速度变化
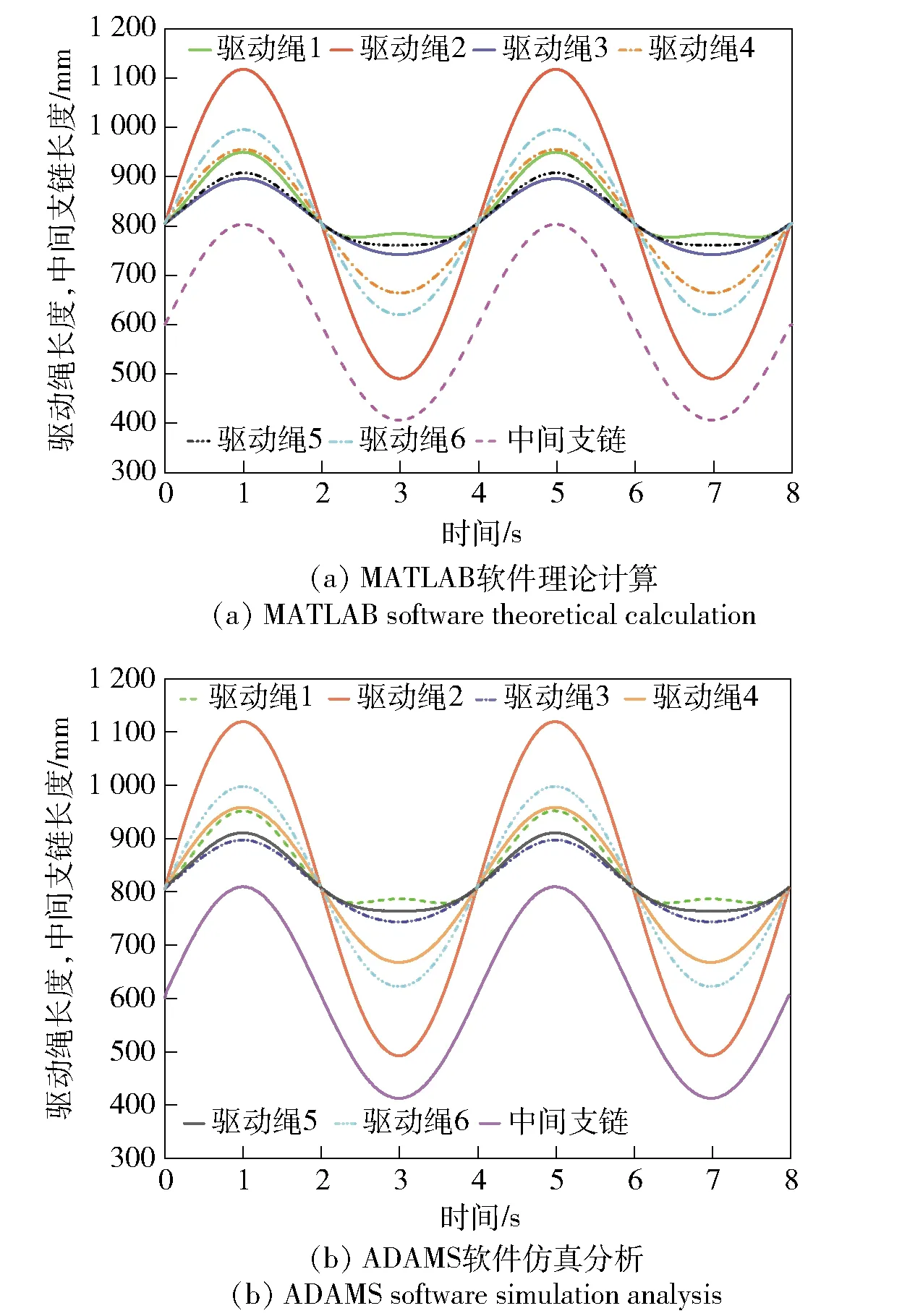
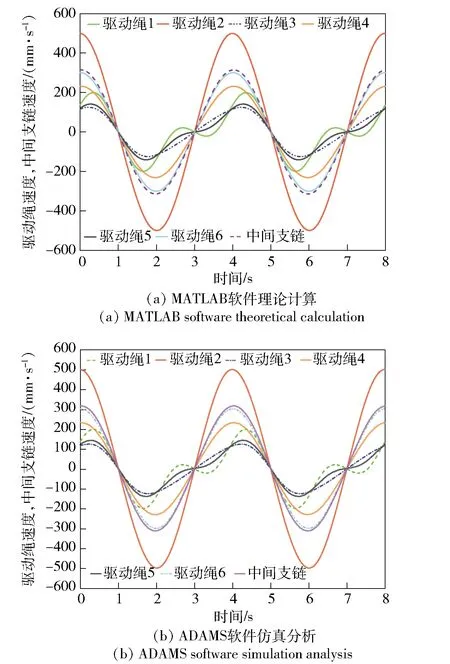
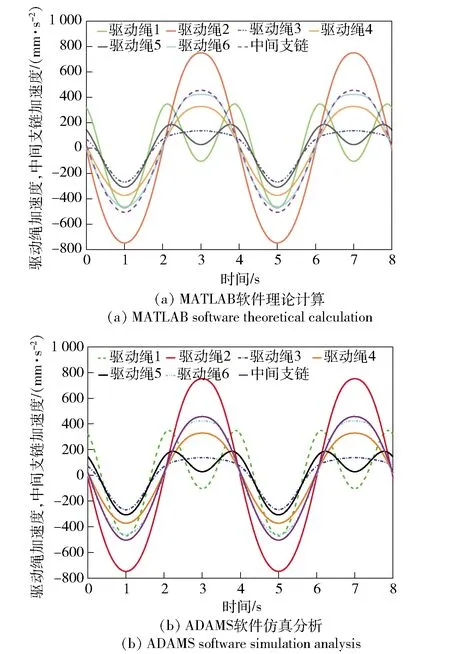

5.2 驱动绳张紧力模拟分析及碰撞干涉检测
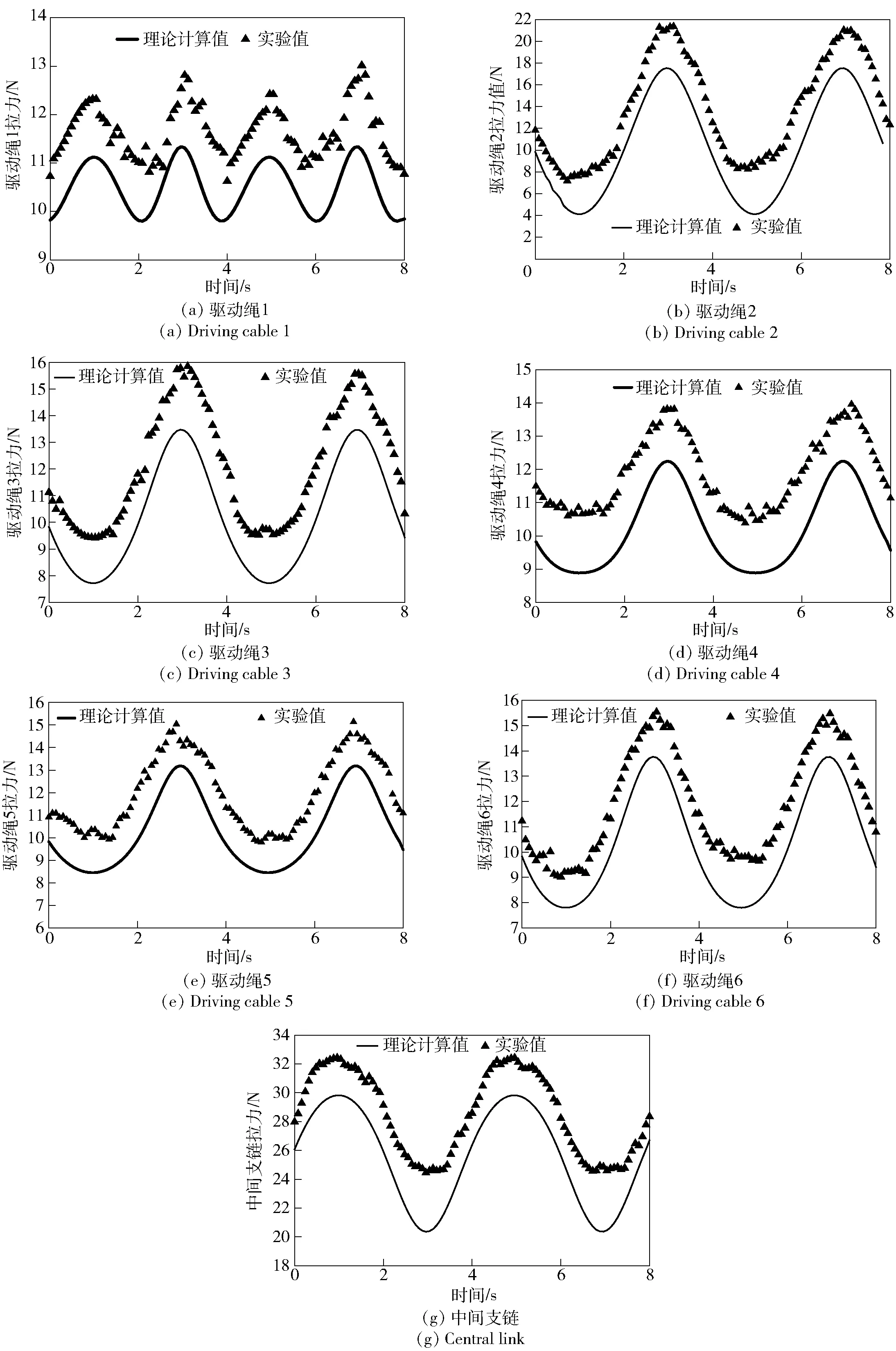
5.3 实验验证分析
6 结论