发挥数学模型的作用
曾庆丰


数学教学实际上是数学模型的教学。本文以“最短路径问题”为例,谈谈在数学模型教学中发展学生数学核心素养的一些思考。
创设情境,孕育数学模型。通过学生已有的知识和生活经验来创设问题情景,并融入新知识的生长点,是进行教学预设的出发点和开展教学活动的发起点。教师可以出示如下题目:如图1,牧马人从A地出发,到一条笔直的河边饮马,然后到B地。牧马人到河边的什么地方饮马,可使所走的路径最短?
我们可以把笔直的河抽象成一条直线马(A地)和帐篷(B地)分别抽象成两个点M、N(图2)。连结MN交直线于点P,由“两点之间,线段最短”可知:牧马人到河边点P处饮马,可使所走的路径最短。教师通过牧马人饮马来创设问题情景,并融入学生熟悉的“两点之间,线段最短”公理,其公理是本节课“最短路径问题”的“最近发展区”。这样设计,既体现了学生的年龄特点和认知规律,又为“最短路径问题”的导入做铺垫。
抽象转化,发展数学建模能力。在教学中,教师应适当地铺垫、启发和引导,注重数学模型发生、发展与形成的探究过程,帮助学生积累建模活动经验。
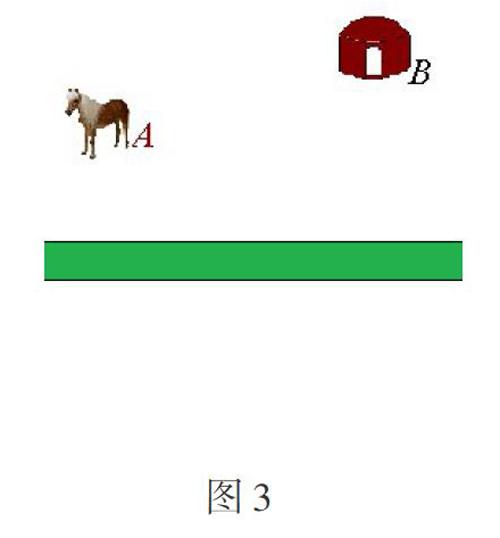
教师可以出示以下例题:如图3,牧马人从A地出发,到一条笔直的河边饮马,然后到B地。牧马人到河边的什么地方饮马,可使所走的路径最短?教师可以引导学生把河抽象成一条直线马(A地)和帐篷(B地)分别抽象成两个点M、N(如图4)。现在问题便转化为:在直线上求作一点P,使“PM+PN”最短。
由上面的引例,我们可以这样引导学生:如果点N在直线的另一侧就好了,可不可以转化呢?也就是说,能不能在直线的另一侧找到一点N',使点N'和N点到直线上任意一点的距离都是相等的呢?不改变问题的实际背景和结论,只改变帐篷的位置,一是减少背景对学生思维的干扰,保持思维的连贯性;二是启迪学生将新问题转化为旧知识,感受转化的自然性与合理性。
演绎推理,发展推理论证能力。教学中,教师应注重数学模型在形式化几何命题中的计算、演绎、推理,并渗透知识之间的内在联系和逻辑关系。
教師可以出示如下例题:如图5,设正三角形ABC的边长为2,M是AB边上的中点,P是BC上任意一点,PA+PM的最大值和最小值分别记为s和t,求s2-t2的值。
由于点P是BC边上任意一点,当点P与点C重合时,PA+PM的值最大,此时,①[s=CM+CA=][CA2-AM2+CA=2+3];作点M关于BC边的对称点N,连接AN交BC边于点P,连接MP,则“PA+PM”的值最小。连接CM、CN,由中垂线的性质和等腰三角形的“三线合一”,得CN=CM=[3],∠1=∠2=∠3=300。②在Rt△ACN中,[AN=AC2+CN2]=[7]。综合①、②,得:[s2-t2=(2+3)2-(7)2=43]。
摆脱模型的实际背景,从形式化的几何命题出发,将模型嵌入等边三角形中,并且融入动点问题,旨在增加问题的宽度。在求最小值时需要运用等边三角形、勾股定理、中垂线等相关知识,让学生在分析、转化、计算、推理等思维活动中,提升运算求解和推理论证的能力。
(作者单位:襄阳市第七中学)
责任编辑 张敏

