再生混凝土冻融损伤可靠性分析

焦隽隽，朱俊锋

(1.河南科技大学应用工程学院，三门峡 472000；2.三门峡职业技术学院，三门峡 472000;3.河南科技大学土木工程学院，洛阳 471000)

0 引 言

近年来，一带一路战略思想逐步推进落实，我国基础建设进入又一个新高潮，破旧建筑物拆迁改造，产生大量的废弃混凝土，给生态环境造成严重的影响，我国提倡绿色可持续发展，因此再生混凝土的研究和推广显得越为重要，但由于再生骨料的自身缺陷以及在加工过程中产生的内部微裂缝，使得再生混凝土在应用中产生很多问题，其耐久性便是最突出的问题之一，在我国西北和东北地区，季节更替变化大，由于其特殊的气候条件，再生混凝土的抗冻融耐久性问题较普通混凝土也越发凸显，对其抗冻性能的研究成为许多专家和学者关注的焦点。

Medina等[1]研究了冻融循环对再生混凝土裂缝的影响，测定出了骨料和界面过渡层平均和最大裂缝宽度，得出随冻融次数增加内部裂缝逐渐加深，导致其抗冻性降低；陈爱玖等[2]进行了在冻融条件下再生混凝土损伤模型的研究，表明其模型预测结果与工程实际冻融损伤较符合；齐振麟[3]对冻融后再生混凝土重复荷载下本构关系进行研究，分析建立了卸载及再加载曲线方程，得出了卸载及再加载曲线参量与冻融次数间的关系式，建立了本构模型；陈钿渊[4]采用快速冻融法研究了再生骨料强化对再生混凝土抗冻性的影响，试验结果表明级配强化可明显提高其抗压强度，化学强化可较大程度提高其延性、弹性模量，复合强化综合了级配强化和化学强化的优点，对力学性能和耐久性均有显著提升；Yildirim等[5]开展了内部养护对再生骨料混凝土抗冻性能影响的研究，探讨再生混凝土骨料(RCA)代替原生骨料的适宜性，认为RCA的高孔隙率和吸水能力将提供内部养护所需的天然水分，得出在RCA替代率为50%时，内部养护对再生混凝土抗冻耐久性有积极影响；另有学者在再生混凝土抗冻性研究中也取得了较大的突破[6-10]。基于目前国内外研究成果，大多停留在定性研究阶段，分析方法上主要以实验数据描述其性能退化规律，而鲜有采用概率理论对其进行进一步的寿命预测及可靠性分析。

因此，本文以质量损失和相对动弹性模量为指标对抗压强度、劈裂抗拉强度最优配合比下再生粗、细骨料双掺成型混凝土进行抗冻损伤研究，采用Weibull概率分布进行数据处理，对再生混凝土性能退化过程建模进行可靠度分析，并建立可靠度函数描述混凝土可靠性与冻融循环之间关系以此反映其剩余寿命，以期为工程实际提供理论指导及进行相关评估鉴定。

1 实 验

1.1 原材料及配合比

水泥:安定性良好的P·O 42.5级普通硅酸盐水泥，河南某商砼公司提供。粗骨料：由洛阳某公司提供的表观密度为2 760 kg/m3的碎石。细集料：级配良好的河砂，属中砂，细度模数为2.78。水：采用洛阳地区自来水。减水剂：洛阳某公司生产的减水率为20%羟系减水剂。再生混凝土设计强度为C30，配合比为：水泥∶水∶碎石∶砂=1∶0.57∶3.37∶2.09，根据本课题组研究成果[11]，基于抗压强度最优配合比替代率为：再生粗、细骨料分别替代15%、10%，基于劈裂抗拉强度最优配比替代率为：再生粗、细骨料分别替代30%、10%。再生骨料各项性能参数分别见表1、表2。

表1 再生粗骨料性能参数Table 1 Performance parameters of recycled coarse aggregate

表2 再生细骨料性能参数Table 2 Performance parameters of recycled fine aggregate

1.2 试验过程及方法

按设定好的配合比制拌混凝土，将所需碎石、砂、再生骨料混合搅拌2～3 min后加入减水剂、水拌合, 搅拌完成后将拌合物均匀的浇筑在试模内振捣密实抹平。

试件(100 mm×100 mm×400 mm)在标准养护条件下养护后置于(20±3) ℃的水中浸泡4 d做快速冻融试验，按照《普通混凝土长期性能和耐久性能试验方法标准》(GB/T 50082—2009)[12]执行，每个冻融作用30次，每次冻融循环时间大约为4 h。在完全冻结时，试件中心温度控制在(-19±2) ℃，完全融化时，试件中心温度控制在(8±2) ℃。

采用质量损失和相对动弹性模量评价损伤程度[13-15]，质量损失率Wn和相对动弹性模量Pn表达式分别如式(1)、式(2)所示。

(1)

(2)

式中,G0为试件冻融试验前的质量；Gn为试件n次冻融试验后的质量；Pn、fn分别表示试件n次冻融试验后的相对动弹性模量、横向共振频率;f0表示试件冻融循环前的横向共振频率。

基于Weibull概率方法对数据处理[16]，性能的退化量y遵从形状参数my(n)和尺度参数ηy(n)的Weibull概率分布，失效判据为y≥Df时，可靠度和性能退化分布关系如式(3)所示。

(3)

式中,R(n)为可靠度，p为寿命概率，Df为试件性能退化失效阈值。按《普通混凝土长期性能和耐久性能试验方法标准》(GB/T 50082—2009)[12]规定试件相对动弹性模量损失达40%或质量损失达5%时，混凝土试件即达破坏标准，故以下均以0.40、0.05表示。

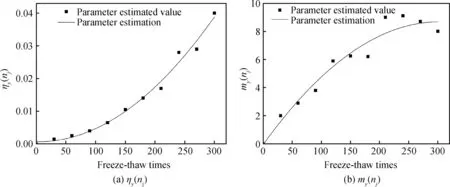
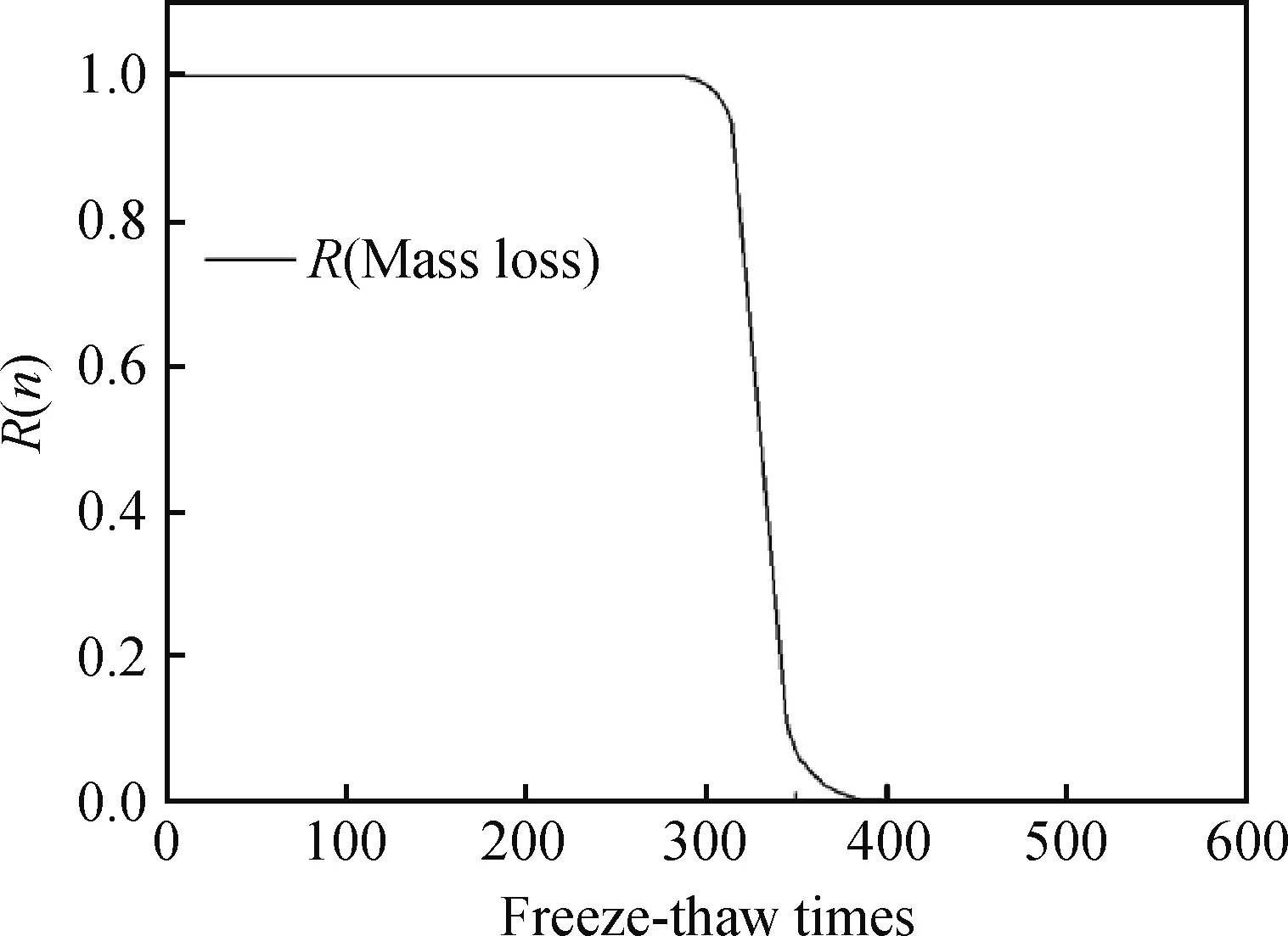
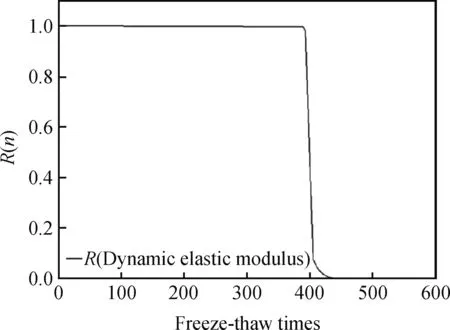
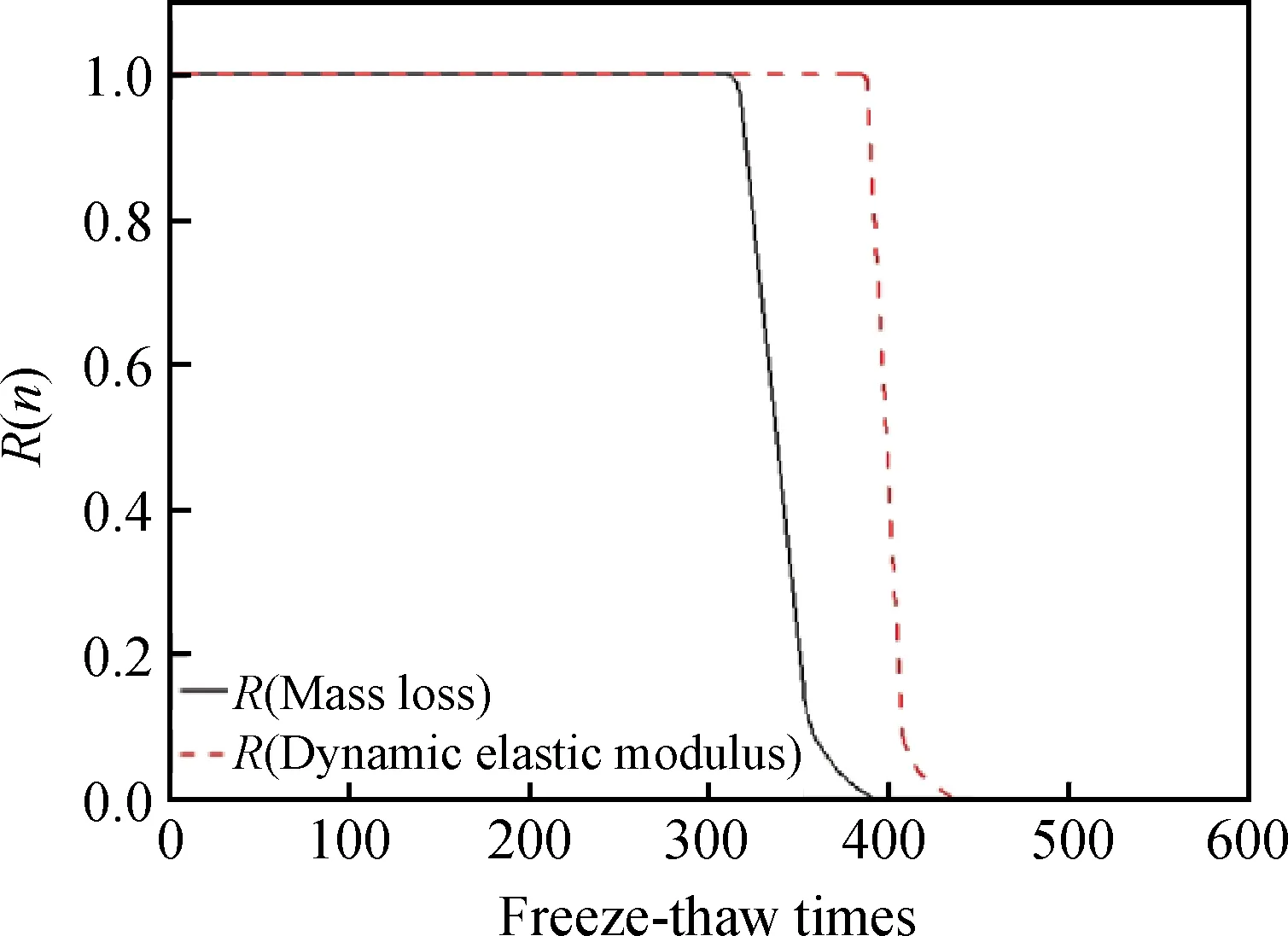
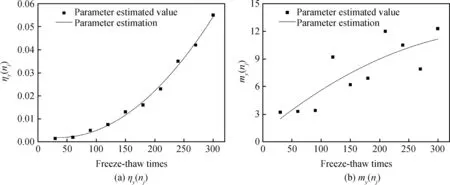
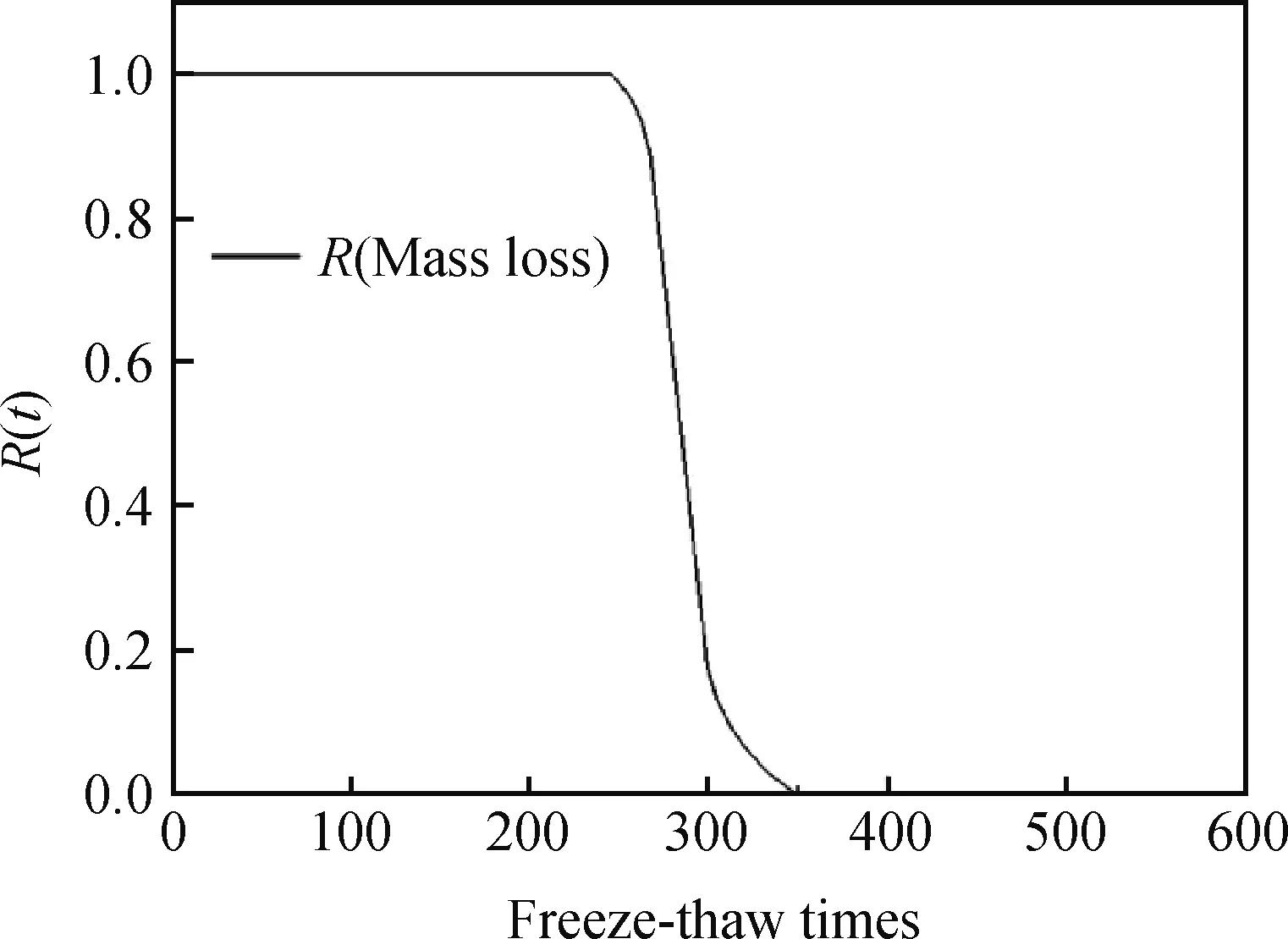
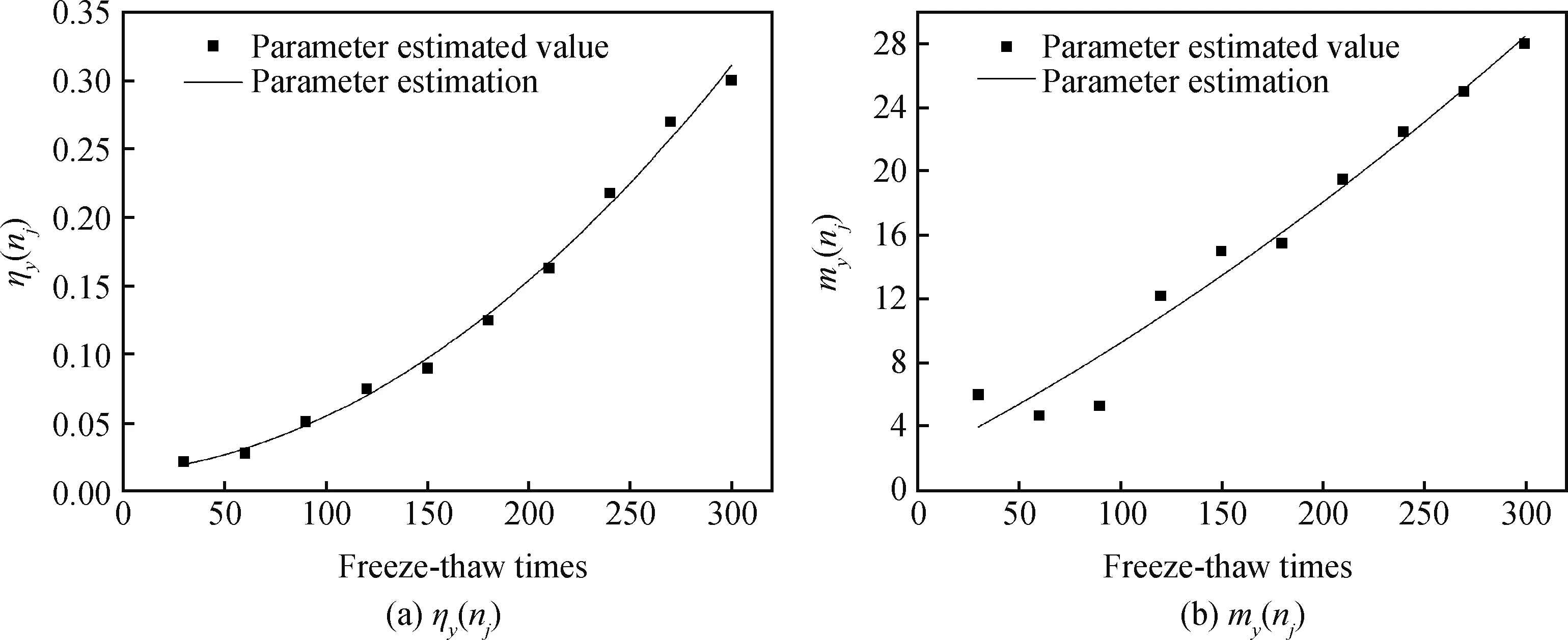
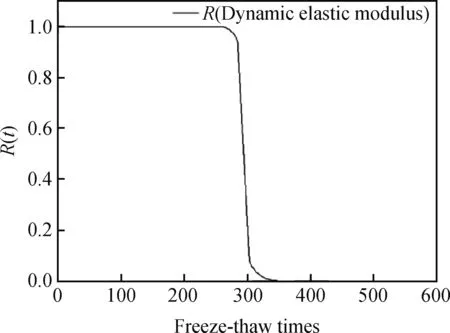
将冻融次数nj时性能退化数据yij排列得到：zj1

(4)

式中,D(n1,n1,k)、C(n1,n1,k)为参数a、σ的BLUE系数。

由极值分布参数点估计a(nj)和σ(nj)得出冻融次数nj时Weibull分布参数点表达式如式(5)所示。

(5)

式中,gn1,n1为m的修偏系数。

2 结果与讨论

2.1 冻融循环下抗压强度可靠性分析

以质量损失和相对动弹性模量评价损伤程度得出耐久性能退化量数据见表3。

表3 耐久性能退化量Table 3 Durability degradation

由表3可知，在冻融循环达到300次时，平均质量损失约为0.039 7，平均相对动弹性模量损失约为0.195 5，均未达到失效阈值，随冻融次数增加质量损失增加较快，表明质量损失指标有较大概率先一步达到失效标准。

根据试验数据，以质量损失为指标的Weibull分布参数点估计ηy(nj)和my(nj)与冻融次数之间有较明确的函数变化关系，ηy(nj)选择指数函数模型进行拟合，即：ηy(nj)=abn；my(nj)选择对数函数模型进行拟合，即：my(nj)=aln(bn)，拟合如表4及图1所示。

表4 参数拟合表Table 4 Parameter fitting table

图1 ηy(nj)和my(nj)的拟合图形Fig.1 Fitting figures of ηy(nj) and my(nj)

由式(3)知Df=0.05,可得出在冻融循环下再生混凝土以质量损失为性能退化量的可靠度曲线如图2所示。

图2 可靠度曲线Fig.2 Reliability curve

由图1可看出参数ηy(nj)拟合精度较高，各点几乎均分布在拟合曲线上，而参数my(nj)拟合精度相对较弱，但也能反映其数值变化规律。

进行以相对动弹性模量为指标的可靠度分析，以退化量估计ηy(nj)和my(nj)的参数点估计值绘制图形，选择拟合精度较高的函数模型，拟合参数表及拟合图形如表5及图3所示。

表5 参数拟合表Table 5 Parameter fitting table

图3 ηy(nj)和my(nj)的拟合图形Fig.3 Fitting figures of ηy(nj) and my(nj)

由式(3)知Df=0.40,可得出在冻融循环下再生混凝土以动弹性模量为性能退化量的可靠度曲线如图4所示。

由图3可看出函数模型各点几乎都分布在拟合曲线上，参数ηy(nj)和my(nj)拟合精度都较高，分别为0.98、0.96。

图4反映了在冻融循环时以相对动弹性模量为性能退化量的可靠度关系，随冻融次数增加，试件可靠度逐渐降低，当可靠度为0时，试件经受约420次冻融循环即达完全失效，在可靠度为0.8时，再生混凝土试件可经受约为380次冻融循环。

图4 可靠度曲线Fig.4 Reliability curve

图5 可靠度曲线Fig.5 Reliability curves

以上两个衡量指标有较大差异，因此综合分析得到可靠度曲线如图5所示。

由图5可看出在再生混凝土耐久性衡量指标中，随冻融次数增加，质量损失和动弹性模量可靠度指标几乎呈同步下降，不同的是质量损失比动弹性模量表现更敏感，在冻融次数达到约300次时，质量损失可靠度指标首先出现下降，而在冻融次数约为400次时，动弹性模量指标才出现下降，可靠度随冻融次数增加逐渐降低，两个衡量指标属竞争失效关系，因此在抗压强度最优配比下，试件经约390次冻融循环即达到失效。

派克汉尼汾公司是一家总部位于美国的跨国公司，自1918年创立至今，派克汉尼汾公司已发展为全球运动和控制领域最大、产品种类最完备的公司。派克汉尼汾公司具有1 000条生产线，制造的制冷空调配件、液压、气动和机电一体化产品应用于约1 200个工业和航空航天市场。

2.2 冻融循环下劈裂抗拉强度可靠性分析

以质量损失和相对动弹性模量评价损伤程度得出的耐久性能退化量数据统计表如表6所示。

表6 耐久性能退化量Table 6 Durability degradation

从表6可知，在冻融循环达到300次时，平均质量损失约为0.054 4,已达到失效阈值，这是因为再生粗骨料替代率较高使得混凝土内部较疏松，致使在冻融循环中质量损失增加明显，而平均相对动弹性模量损失约为0.30，未达到失效阈值，说明在劈裂抗拉强度最优配比下，随冻融次数增加再生粗骨料对质量损失指标影响较大，质量损失指标达到失效阈值，试件即达到失效标准。

根据质量损失为指标的Weibull分布参数点估计ηy(nj)和my(nj)绘制图形，考虑到拟合精度问题，ηy(nj)选择函数模型为：ηy(nj)=anb，my(nj)选择函数模型为：my(nj)=a+bn，参数拟合表及拟合图形如表7及图6所示。

由式(3)知Df=0.05，可得出冻融循环下再生混凝土以质量损失为性能退化量的可靠度曲线如图7所示。

表7 参数拟合表Table 7 Parameter fitting table

图6 ηy(nj)和my(nj)的拟合图形Fig.6 Fitting figures of ηy(nj) and my(nj)

图7 可靠度曲线Fig.7 Reliability curve

由图6可看出参数ηy(nj)拟合精度较高，各点几乎都分布于拟合曲线上，而参数my(nj)拟合图形各点散乱分布于拟合曲线周边，拟合精度较弱，但也可大致反映其数值变化规律。

图7反映了冻融次数与质量损失间的可靠度关系，在劈裂抗拉强度最优配比下，可靠度为0时，再生混凝土试件经受冻融循环次数约为350次时达到完全失效，可靠度为0.8时，再生混凝土试件经受的冻融次数可达到约280次。

以相对动弹性模量为指标进行可靠度分析，以退化量估计ηy(nj)和my(nj)的参数点估计值绘制图形，选择拟合精度较高的函数模型，拟合参数表及拟合图形如表8及图8所示。

由式(3)知Df=0.40，可得出冻融循环下再生混凝土以动弹性模量为性能退化量的可靠度曲线如图9所示。

表8 参数拟合表Table 8 Parameter fitting table

图8表明选择的函数模型拟合精度较高，各点均分布于拟合曲线上及曲线附近。

图9反映了在劈裂抗拉强度最优配比下以动弹性模量为指标的冻融可靠度关系，可靠度为0时，再生混凝土试件可经受约340次冻融循环后达到失效，随冻融次数增加，可靠度逐渐降低，可靠度为0.8时，再生混凝土试件达到失效时可经受约300次冻融循环。

考虑到以上两个指标有所差异，将以上两个指标综合分析得到可靠度曲线如图10所示。

图8 ηy(nj)和my(nj)的拟合图形Fig.8 Fitting figures of ηy(nj) and my(nj)

图9 可靠度曲线Fig.9 Reliability curve

图10 可靠度曲线Fig.10 Reliability curves

从图10可看出在劈裂抗拉强度最优配比下质量损失和动弹性模量两个可靠度与冻融循环之间的关系，当冻融次数达到约为250次时质量损失可靠度出现下降，而动弹性模量可靠度仍然为1.0，表明此配合比混凝土耐久性指标中质量损失比动弹性模量表现更敏感，究其原因为再生粗骨料替代率较高，增加了混凝土内部裂缝及孔隙数量，致使在冻融循环过程中质量损失较大；随冻融次数增加，质量损失与动弹性模量可靠度逐步下降，最终完全失效时所经受的冻融次数较为接近，分别约为350次、340次。

3 结 论

(1)再生混凝土冻融损伤可靠性分析中，质量损失和相对动弹性模量反映了试件随冻融循环变化的规律，基于抗压强度最优配合比，质量损失变化速率较动弹性模量变化速率快，可预测质量损失指标先达到失效阈值，试件经受约390次冻融循环即完全失效；基于劈裂抗拉强度最优配合比，质量损失指标在冻融次数300次时，已先达到失效阈值，试件最终完全失效时经受的冻融次数较接近。在两个性能退化指标中，质量损失比动弹性模量更敏感。

(2)Weibull概率分布可有效描述再生混凝土试件抗冻性能退化趋势，基于试验数据建立可靠度函数可直观反映试件可靠性并反映试件的剩余寿命，以此可为实际工程提供相关理论指导及维修诊断。