区间粗糙数排序比较仿真及其在物流领域中的应用

翁世洲,吕跃进

(1.广西民族师范学院 经济与管理学院,广西 崇左 532200； 2.广西大学 数学与信息科学院,南宁 530004；3.广西科技大学 鹿山学院,广西 柳州 545616)

0 引言

区间粗糙数作为近年来兴起的一种新的数据形式,以粗糙集和序信息系统为理论基础[1],在处理不确定、不一致和不精确数据方面显示出其独特优势.作为区间数和粗糙集的联合推广形式,区间粗糙数的数据区间从一个变为两个,形如([a,b],[c,d]),其中c≤a≤b≤d.因此,如何将区间粗糙数与实数空间对应起来,进而解决多属性决策中的相关问题尤为重要.

在对区间粗糙数进行排序比较的研究领域,国内学者已取得一些初步成果.如曾玲等人[2]1758将区间粗糙数的期望值定义为(a+b+c+d)/4,以期望值大小作为区间粗糙数排序的依据.王坚强等人[3]则进一步引入区间粗糙数的随机变量,使得每个对象在各个准则下的取值对应多个区间粗糙数和相应的概率取值,并通过区间粗糙集结算子(WIRDAA)对准则下的不同取值进行集结以达到排序目的.钱伟懿等人[4]在定义加权平均算子(IRWA)与加权几何算子(IRWG)的基础上,提出了区间粗糙数比较的可能度公式,并讨论了相关性质,最后通过IRWA算子进行排序决策.吕跃进等人[5]提出了一种考虑决策者偏好的加权期望值计算方法,孙琪恒[6]通过统计理论中的极大似然估计确定其数学期望进而排序,张芳馨等人[7]通过定义区间粗糙数的可能度然后进行排序,曾雪兰等人[8]将集对分析与联系数的概念引入区间粗糙数,然后将区间粗糙数转化为联系数进而加以比较和排序.此外谢凤平等人[9]讨论了基于区间粗糙数互补判断矩阵的排序问题,吕跃进等[10]对基于区间粗糙数信息系统的覆盖分类冗余度与属性约简进行了相关研究并取得一定成果.

在区间粗糙数分布类型的研究领域,国内近年来也取得一些成果,如田瑾等人[11]提出了带参数的区间粗糙数问题,考虑了非均匀分布下的区间粗糙数比较问题,并给出了集结算子.夏晓东等[12]在其成果中也采用了带参数的区间粗糙数,并结合理想点法给出了多属性决策方法.尽管这些文献开始意识到不能忽略区间粗糙数的分布类型去讨论其相关性质,但在分布类型的研究上还有待进一步深入.

从现有文献来看,尽管研究区间粗糙数的排序方法已经取得诸多成果,但是在将区间粗糙数转化为实数的过程中,不可避免需要涉及的一个问题,即区间粗糙数分布类型的假定.在上述文献中,文献[6-7]给出了区间粗糙数服从均匀分布的假定,文献[8-9]给出了区间粗糙数服从正态分布的假定.文献[2-5]虽未明确表明其研究的区间粗糙数服从何种分布,但根据其所定义的数学期望等度量公式来看,研究者们也更倾向于数据服从均匀分布或正态分布.但在实际问题中,区间粗糙数在给定范围内的取值可能服从各种不同类型的分布,如常见的还有指数分布、二项分布、泊松分布等形式,若区间粗糙数并非服从简单的均匀分布或正态分布,则上述文献所定义的相关公式(如数学期望)将不再适用,这将给区间粗糙数的比较与排序带来新的难题,但若针对每一种分布类型去研究其复杂的数学机理,进而定义数学期望、方差的公式再用于比较,其晦涩的数学推理将成为阻碍区间粗糙数理论研究发展的一大障碍.

鉴于此,本文将对区间粗糙数所服从的不同分布类型进行假定,从常见的均匀分布、正态分布、二项分布、指数分布入手展开相应分析.在本文中,将避开复杂的数学理论,直接考虑随机变量在区间粗糙数给定范围内的取值情况,并通过MATLAB软件产生符合特定分布律的随机数,模拟这一情形,其关键在于如何将区间粗糙数的参数与不同分布类型的参数对应起来.对不同区间粗糙数的排序比较问题,不再使用数学理论进行推导,在服从给定分布的情形下,用MATLAB软件进行大数据模拟,根据每次产生的不同随机数进行比较,统计总体结果并对不同的区间粗糙数比较排序.借助于软件的强大功能并通过快速运算在一定程度上替代数学推理,但能达到相同的效果,为人工智能的发展提供参考和借鉴.

1 区间粗糙数基本概念

定义1[16]设U是一个论域,并且是一个表示概念的集合,其下近似和上近似分别定义为

(1)

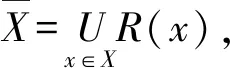
(2)

其中:R(x)={y∈U|y≅x},R-1(x)={y∈U|x≅y}.

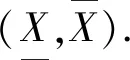
定义3一个区间粗糙数是下近似和上近似均为区间的粗糙集,记为([a,b],[c,d]),其中c≤a≤b≤d.

例如某项目的投资额用区间粗糙数表示为([4,6],[3,7]),对于这一表达的含义,解释为“投资额在4万～6万元之间是肯定的,在3万～7万元之间是可能的”[2]1757,笔者认为这一解释在逻辑上存在些许问题,既然取值在4万～6万元之间是肯定的,自然就无法取到超出这一范围的值,也就不存在于3万～7万元之间取值的提法.鉴于此,本文认为对于区间粗糙数的语义解释可有以下两种:

1)若该项目的投资额在4万～6万元之间,是肯定能被投资者接受的,若投资额在3万～7万元之间,是可能被投资者接受的.这一解释是站在投资人的角度,对不同投资额的接受程度进行解释,且“肯定”与“可能”的语义与粗糙集的下、上近似相一致.

2)该项目的投资额肯定会在3万～7万元之间,但实际上更有可能在4万～6万元之间.这一解释是站在项目本身的角度,对其投资额可能的取值范围进行描述,以不同的概率取对应值,这一解释虽使得“肯定”与“可能”的语义与粗糙集不相一致,但与绝大多数实际情况是相符的.

2 各类随机分布下的区间粗糙数模型

2.1 均匀分布

若区间粗糙数ξ=([a,b],[c,d])在给定区间上服从均匀分布,则对应的数学期望与方差分别为

(3)

此时ξ在区间[a,b]取值的概率为

(4)

在使用MATLAB软件进行仿真时,利用系统自带的函数unifrnd可以产生服从均匀分布的随机数,语法格式为

M=unifrnd(a,b):产生在区间[a,b]上服从均匀分布的随机数.

2.2 两阶段均匀分布

本文所指的两阶段均匀分布,其基本提法来源于文献,意为ξ在区间[c,d]上服从均匀分布的基本假定,但由于区间粗糙数的初衷为ξ“更有可能”在[a,b]上去取值,鉴于此,在均匀分布的基础上,将ξ所对应的区间分为两部分,即[a,b]与[c,a]∪[b,d],然后ξ在[a,b]与[c,a]∪[b,d]各自服从均匀分布,但显然应在[a,b]上有更大的概率密度[18]820.

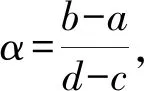
(5)

公式(5)意为ξ在[a,b]上取值的概率密度是在[c,a]∪[b,d]上取值的概率密度的k倍,解之得

(6)

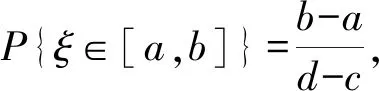
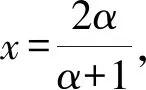
在使用MATLAB软件进行仿真时,无法直接产生此种类型的分布,因此只能借助于均匀分布的方法间接产生.步骤如下:

1)使用flag=unifrnd(0,1)产生[0,1]上服从均匀分布的随机数；

2)若flag≤x,则使用M=unifrnd(a,b)产生区间[a,b]上服从均匀分布的随机数；否则转下一步；

3)使用flag2=unifrnd(0,1)产生[0,1]上服从均匀分布的随机数；

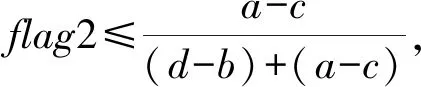
注:上述第4步的flag2,意在使得ξ在[c,a]∪[b,d]}按区间长度所占比例对应产生随机数,避免因为[c,a]∪[b,d]}不是一个连续区间而无法直接产生随机数.

2.3 正态分布

若区间粗糙数ξ∈([a,b]∪[c,d])在给定区间上服从正态分布N(μ,σ2),由于正态分布对应的定义域为(-∞,+∞),区间[c,d]只是定义域中的一段,如何通过区间粗糙数的端点来界定正态分布的参数值得考虑,为避免在生成正态分布随机数时产生溢出或越界现象,根据正态分布的3σ准则,使得P{ξ∈[c,d]}≥Φ(3)-Φ(-3)=0.997 4,即溢出的概率仅为3‰以下,使随机数以尽可能大的概率落入给定区间[c,d]上.

由准则可知正态分布下对应的数学期望与标准差为

(7)

此时ξ在区间[a,b]取值的概率为

(8)

在使用MATLAB软件进行仿真时,可直接使用系统自带函数normrnd(MU,SIGMA)产生均值为°MU,标准差为°SIGMA°的正态随机数.步骤如下:

1)计算区间粗糙数ξ=([a,b],[c,d]}所对应的正态分布均值MU和标准差SIGMA；

2)使用M=normrnd(MU,SIGMA)命令生成均值为°MU,标准差为°SIGMA°的正态随机数；

3)若M∉[c,d],表明数据溢出,则重新生成,直至符合要求为止.

2.4 二项分布

若区间粗糙数ξ∈([a,b],[c,d])在给定区间上服从二项分布b(n,p),其中二项分布X～b(n,p)的两个参数分别表示最大实验次数和单次实验中某事件发生的概率.为使得区间粗糙数服从二项分布,对应关系如下.

由于随机变量应在0～n之间取值,为了对应,需先将ξ∈([a,b],[c,d])转化为ξ′=([a-c,b-c],[0,d-c]),此时则有n=d-c,二项分布的数学期望E(X)=np代表最有可能发生的位置,由于ξ′=([a-c,b-c],[0,d-c]),更有可能在[a-c,b-c]之间取值,因此有数学期望的近似公式:

(9)

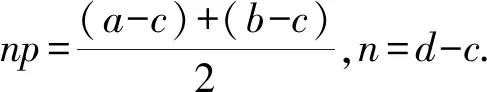
(10)

将ξ=([a,b]，[c,d])转化为ξ′=([a-c,b-c]，[0,d-c])的合理性在于:

E(X+C)=E(X)+C,D(X+C)=D(X),

(11)

即数据进行线性变换后不会改变随机变量的数字特征和分布规律,因此这种转换是合理的.

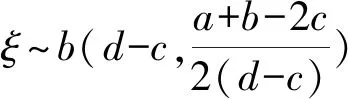
在使用MATLAB软件进行仿真时,可直接使用系统自带函数°binornd(n,p)产生实验次数为°n,单次试验发生概率为p的二项分布随机数,具体步骤如下:

1)将区间粗糙数ξ=([a,b],[c,d])转化为ξ′=([a-c,b-c]，[0,d-c])；

2)由公式计算所需参数n,p；

3)使用M=binornd(10n,p)命令产生0～10n上的二项分布随机数；

4)令M=M/10+c将数据还原到区间[c,d]上.

2.5 指数分布

X服从参数为θ的指数分布的概率密度为

(12)

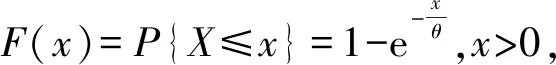
若区间粗糙数ξ=([a,b],[c,d])在给定区间上服从指数分布,为拟合指数分布,需做与二项分布类似的数据变换,即ξ′=([a-c,b-c]，[0,d-c]).由于指数分布的有效定义域为(0,+∞),而ξ对应的区间[0,d-c]只是其中很小一部分,但占据着极大概率.因此,在确定参数θ时应尽可能使得产生的随机数落入区间[0,d-c]上.与正态分布类似,采取以1-α的概率保证这一结论的成立,即

(13)

其中x0=d-c.则解之得

(14)

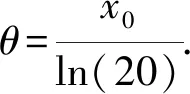
在使用MATLAB软件进行仿真时,可直接使用系统自带函数exprnd(EX)产生均值为EX的随机数,具体步骤如下:

1)将区间粗糙数ξ=([a,b],[c,d])转化为ξ′=([a-c,b-c]，[0,d-c])；

2)由公式计算对应参数θ；

3)使用M=exprnd(θ)命令产生(0,+∞)上的指数分布随机数；

4)若M>d-c,表明数据溢出,则返回上一步重新生成随机数,否则转下一步；

5)令M=M+c将数据还原到区间[c,d]上.

2.6 无规律随机分布

本文所指的无规律随机分布,指不存在任何明显规律,或者是尚未发现其规律,抑或是难以用常见的分布类型进行表达的情形.即ξ=([a,b],[c,d])在区间[c,d]上的取值几乎是完全随机的.

MATLAB软件本身没有提供完全无规律的随机数,因此在仿真时,实际上仍是产生服从某种常见分布的随机数,但是在选择分布类型时是以随机原则进行的.其步骤可简单概括为:

1)使用某一分布函数随机产生一个k∈[1,n]之间的整数随机数,即k=1,2,……,n；

2)根据k值选择预先设定好的随机数类型；

3)根据上一步选择的分布类型使用对应的函数产生相应随机数,具体步骤如前所述.

例如预先设定了五种分布,则取n=5,若在步骤1中产生的数字为1,则按第一种分布类型(假定为均匀分布)产生随机数,在第二次试验时,若在步骤1中产生的数字为3,则按第三种分布类型(假定为正态分布)产生随机数,以尽可能达到完全随机的目的.

上述做法看似随机数是由有规律的分布类型所产生,但由于在循环仿真中每次产生的随机数实际上是由不同分布混合而成,而这些常见分布的混合并不服从某一常见分布,从而实现模拟无规律随机分布的目的.

在统计领域,对于随机变量的分布类型,远远不止上述几种,如还有几何分布、超几何分布、泊松分布、卡方分布、t分布等各种类型,限于篇幅,本文无法一一列举并做讨论,对于其他分布,可按类似的方式确定区间粗糙数的边界值与相应分布类型参数之间的对应关系,然后进行转化.值得说明的是,不同分布之间并无优劣之分,不同分布的存在仅仅是因为有其各自适用的问题背景.至于在实际问题中,不同的属性或指标数据符合何种分布,需要根据问题特性以及行业经验来加以确定,不是数学本身可以做出强制性规定的.如在排队系统中,顾客到达率一般服从泊松分布或指数分布,乘客候车时间则服从均匀分布,考试成绩一般服从正态分布等.在同一个问题中,不同指标可能服从不同的分布类型,不能采用统一的分布假设进行处理.

3 区间粗糙数比较的仿真研究

为研究不同分布类型对区间粗糙数实际取值的影响,本文分别用MATLAB程序将上述分布类型对应的产生随机数算法加以实现,并对表1中不同的区间粗糙数进行两两对比分析,得到的实验结果如表2所示(实验环境:Windows7 32位操作系统,CPU AMD N830三核,内存2GB,硬盘500GB).

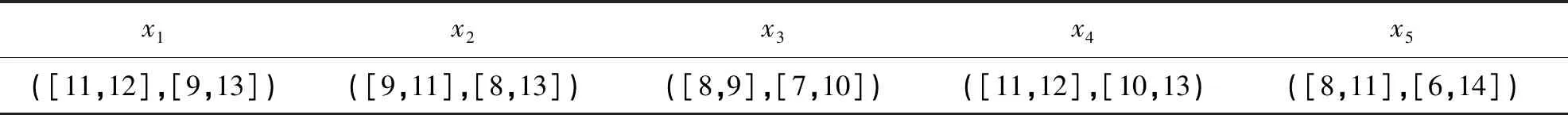
表1 仿真分析原始数据

在表2中,仿真次数N=10 000,i和j分别表示表1中的对应区间粗糙数xi和xj的对比,fk表示第k种分布下,xi>xj的次数,ek表示第k种分布下,xi=xj的次数(只有二项分布和无规律随机分布下会出现此种情形),pk表示根据仿真结果计算出的xi>xj的概率,则P{xi>xj}=fk/N.

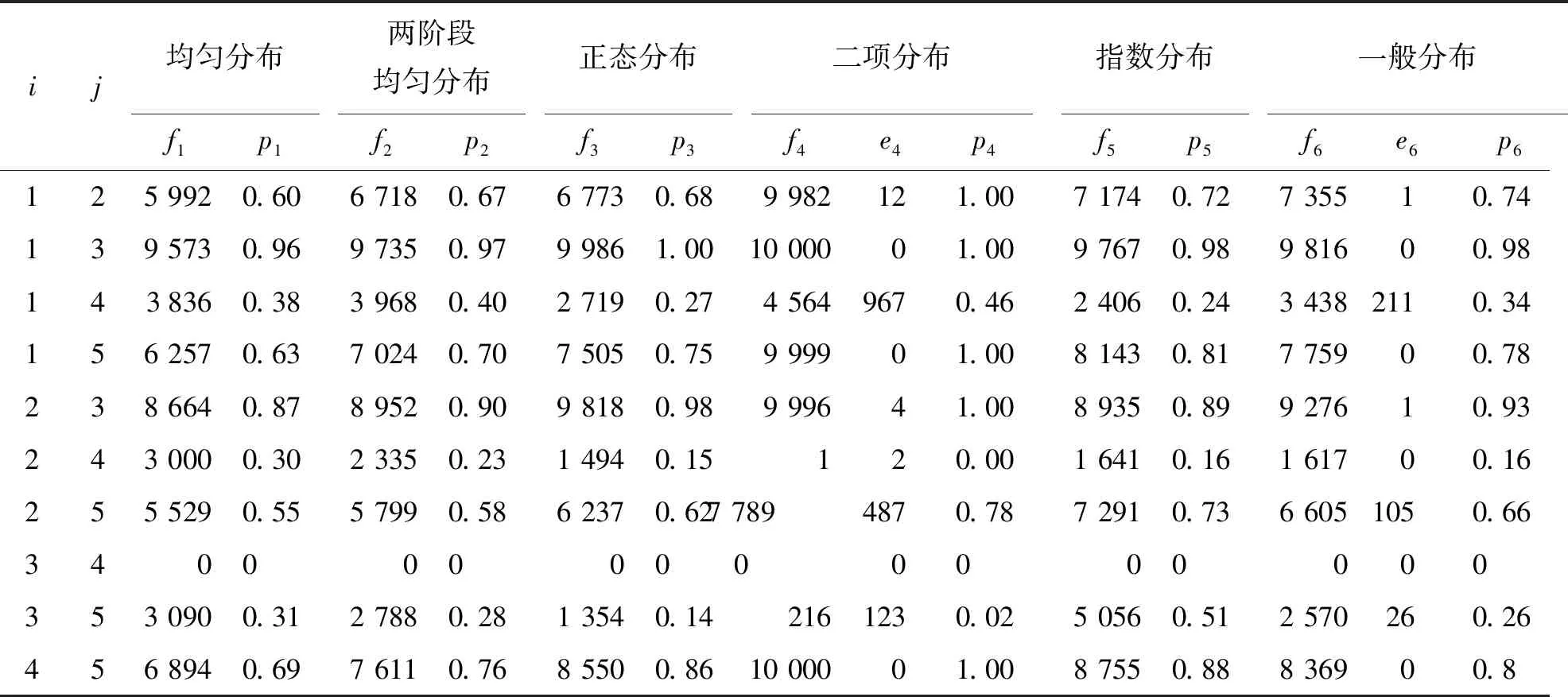
表2 仿真分析统计结果表

基于本文比较方法,可得不同分布下的区间粗糙数排序关系如表3所示,为了验证本文算法,将文献[2]和文献[4]给出的排序方法应用于本例中,对比结果如表3所示.

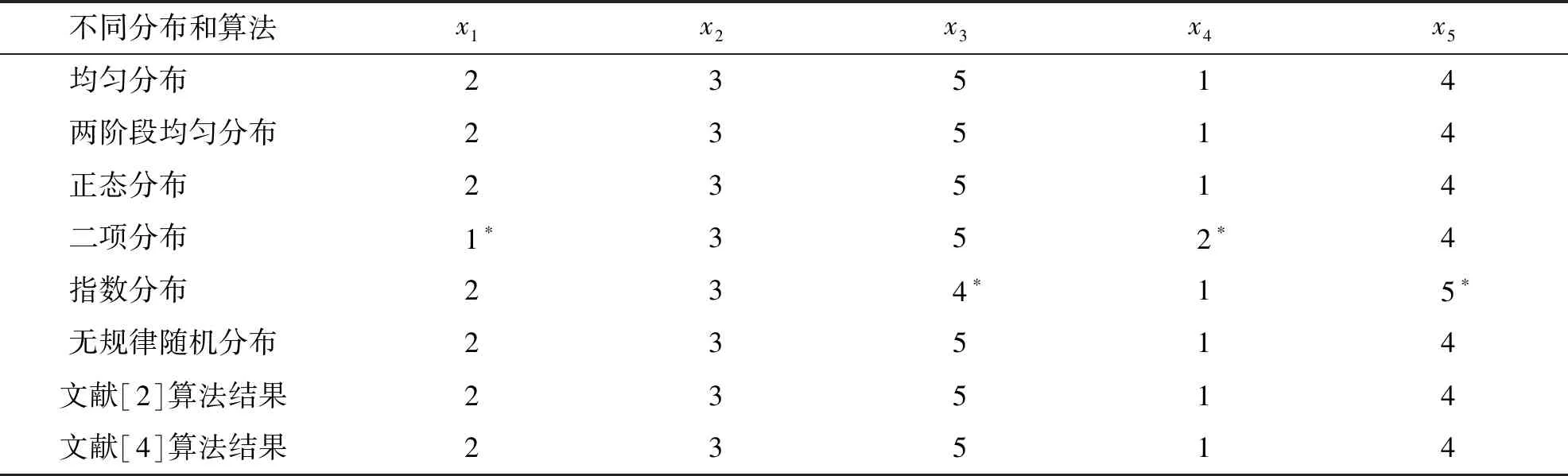
表3 本文算法与类似文献对比

注:表中带*的数字,表明该方法下的排序与其他各排序方法存在不一致的情况.

由表2的仿真结果可以看出,给定两个区间粗糙数,当给出不同的分布类型假设时,所得到的优劣比较概率存在较大差别.以x3,x5的比较为例,在指数分布下,x3与x5不相上下,甚至x3还稍微占优,但在其他分布类型下,比较结果均为x3显著劣于x5,整个占优概率区间跨度为[0.02,0.51],差异性较大.

由表3可以看出,尽管大多数分布下得出的排序结果一致,均为x4≻x1≻x2≻x5≻x3,该结果与文献[2]和[4]一致,但也存在特殊情况,例如在二项分布中,x1与x4出现了逆序情况,在指数分布中,x3与x5同样出现了逆序.

仿真结论:区间粗糙数分布类型的不同假定对于区间粗糙数大小的比较有一定影响,甚至可能会在不同的分布类型下得到完全不同的结论,因此在现实问题的区间粗糙数比较研究中,有必要根据实际情况对区间粗糙数所服从的分布类型进行研究,从而做出合理的假定.

为进一步验证对不同分布类型假定下的合理性,特地选取x1在二项分布和指数分布下的随机数取值结果进行分析,取值规律如图1、图2所示.

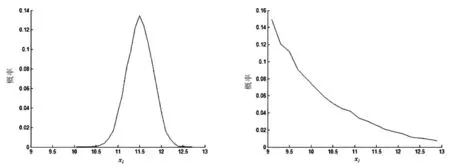
图1 二项分布下的x1取值效果图 图2 指数分布下的x1取值效果图

从图1、图2可以看出,在对x1进行的10 000次仿真模拟中,产生的随机数服从二项分布和指数分布的拟合效果与相应分布的理论情形基本吻合,说明随机数模拟算法达到了预定目标.同时可以看出,尽管x1都是在[9,13]之间取值,但是由于分布类型不同,其取值的集中区间明显不同,在二项分布下,x1取值主要集中在[11,12],基本呈对称分布,而在指数分布下,x1取值则主要集中在[9,10],并且取值概率逐渐下降.

4 区间粗糙数在物流中心选址中的应用

4.1 案例背景

物流配送中心的选址关系到物流运输成本、车辆调度等诸多问题,越来越受到企业重视.因此,在企业物流规模的扩张中,何处选址需要企业进行科学分析.假定某公司现有5个候选地址可供建立物流配送中心,企业在选址时考虑的主要因素包括成本、期望收益、管理效益和风险四个方面.各指标对应的数据由于是预估值,因此都是以区间粗糙数的形式给出,为了避免指标间的数据类型差异,成本数据表示成本节约量、风险数据表示规避和防范风险能力,因此所有数据都是效益型数据.原始数据如表4所示,其中a1,a2,a3,a4分别表示节约成本、期望收益、管理效益和规避风险四个方面的评价指标.

表4 物流中心选址原始数据

对于区间粗糙数形式的多属性决策问题,首先需要解决两个难题,一是区间粗糙数向实数的转化,这就涉及数据分布的假设问题,而传统方法在求其期望值时基本是按照均匀分布或正态分布进行处理,且对所有指标均是如此,缺乏科学依据.二是多属性的数据集结问题,一般方法如层次分析法、模糊综合评价等均需要确定不同指标的权重,然后在此基础上进行集结,但权重的确定是一个极为主观的问题,不同的权重完全可能导致不同的排序结果.综合上述分析,拟采用本文所提的方法,一是根据不同指标拟合不同的分布类型,二是避免不同属性集结过程中的数据归一化处理和权重确定问题,最大程度上做到客观公正.

4.2 排序比较

根据指标本身的数据特性,同时为了进一步验证本文所给出的不同分布形式,故假定节约成本和期望收益服从均匀分布,管理效益服从二项分布,规避风险服从指数分布.根据上节中的MATLAB仿真算法进行再次仿真,得到的结论见如下表5.

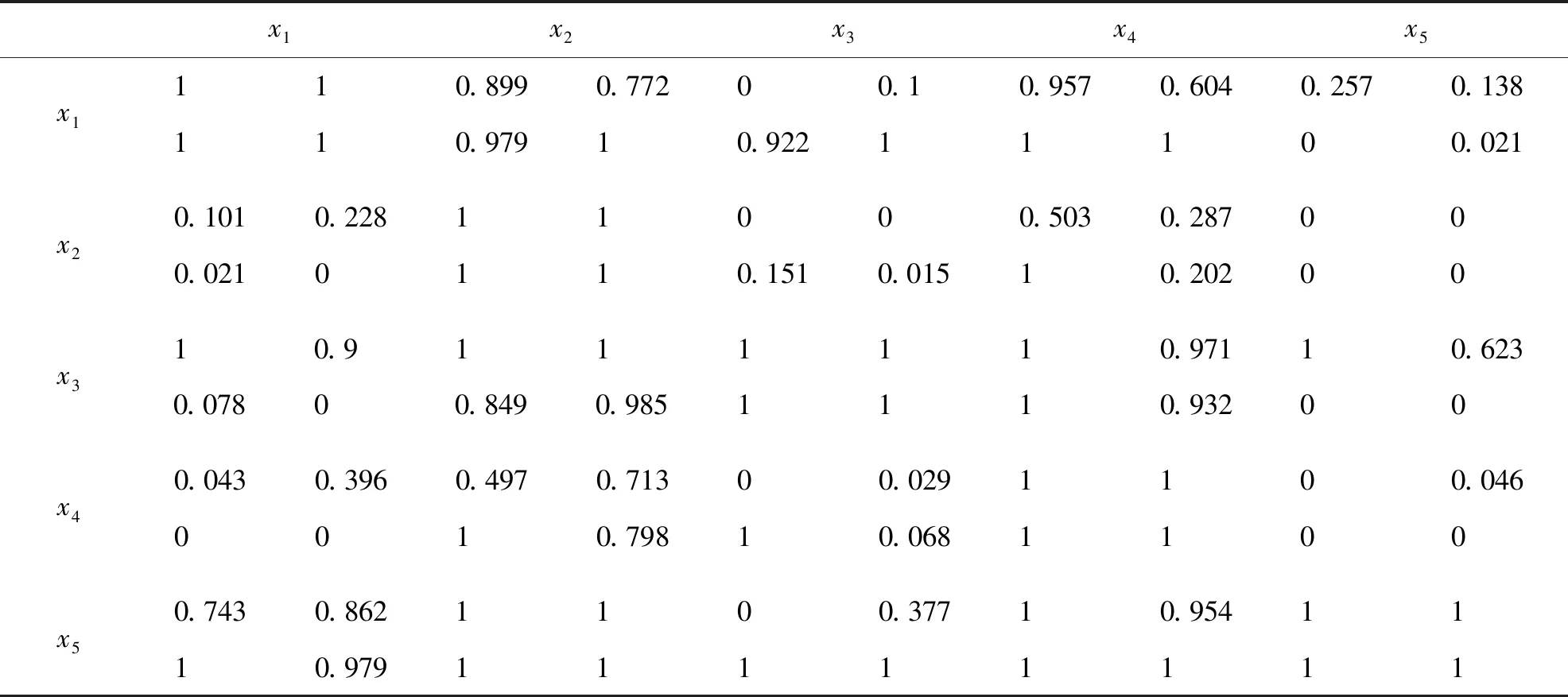
表5 物流中心数据两两比较仿真结果

表5中,第一行第二列表格中的(0.899,0.772,0.979,1)表示x1与x2相比,在四个属性下各自的优势度(仿真次数N=10 000),即Pa1(x1>x2)=0.899,Pa2(x1>x2)=0.772,Pa3{x1>x2}=0.979,Pa4{x1>x2}=1,其他数值可做类似解释.

若取α=0.5表示优劣比较的下限,则根据优势关系的构造方法[18]823,可得

进而根据优势关系排序法[19],可得五个方案的排序结果为

x5≻x3≻x1≻x2～x4.

排序结果表明,在5个候选地址中,x5是最佳选择,x2和x4则不相上下,且均不宜作为选址方案.这与文献[18]的排序结果一致,说明了本文对区间粗糙数分布的假定是合理的.

5 结语

本文通过对区间粗糙数所服从的分布做出合理假定,讨论了六种不同分布类型下的区间粗糙数取值与分布类型参数之间的关系,并给出了如何使用MATLAB软件进行仿真分析的相关算法.通过样例数据,在MATLAB软件下对各种分布类型的区间粗糙数进行比较分析,得出分布类型对区间粗糙数的比较存在一定影响的结论.此外,论文还将这一方法应用到物流领域,用于辅助进行物流中心的选址决策,结果与其他文献一致.

通过MATLAB软件进行数据仿真分析,可大大降低分析难度,避开晦涩难懂的概率求解问题,具有更好的推广价值.今后我们将进一步讨论其他分布类型下的区间粗糙数比较问题,并进一步推广到其他应用领域,以不断丰富和完善多属性决策的理论方法.