多种载荷作用下H 型垂直轴风力机叶片的结构优化
张 旭,李召暄,李 伟
(1. 天津工业大学天津市现代机电装备技术重点实验室,天津 300387;2. 天津城建大学能源与安全工程学院,天津 300384)
0 引 言
叶片旋转过程中受到重力、离心力和气动力的耦合作用,某些位置会产生较大的应力应变集中,从而降低风力机的可靠性和寿命[1-3]。空心薄壁结构的叶片多采用玻璃纤维增强复合材料,可通过内部结构和纤维铺层的优化设计来提高其强度和刚度[4-5]。此外,作为最主要动力来源的气动力是随风速时刻变化的。因此,准确、实时地提取气动力并进行多种荷载作用下叶片的结构几何参数和复合材料铺层的优化,对保障风力机安全、稳定运行具有重要的理论指导意义和工程应用价值。
国内外学者在风力机叶片结构优化方面取得了一系列研究进展。Jureczko 等[6]和Barnes 等[7]采用遗传算法进行水平轴风力机叶片多准则优化,通过改变铺层厚度、主梁宽度和腹板参数以减轻叶片质量。Hu 等[8]和Zhu 等[9]以降低材料成本和叶片重量为设计目标,结合有限元分析和进化算法优化水平轴风力机叶片的铺层参数及主梁宽度等。Sun 等[10-12]利用遗传算法和有限元法、Albanesi 等[13-14]将遗传算法与逆有限元法和人工神经网络相结合进行水平轴风力机叶片的铺层优化。廖猜猜等[15]以获得最大一阶挥舞频率为设计目标,优化水平轴风力机叶片主梁帽的铺层厚度及位置。冯消冰等[16]以水平轴风力机叶片层压板的强度最大为设计目标,利用遗传算法优化铺层角度。汪泉等[17]基于粒子群算法和有限元法优化水平轴风力机叶片的主梁位置和层合板厚度。田德等[18]和陈进等[19-20]约束水平轴风力机叶片的最大变形、振动频率、强度等,采用粒子群算法进行铺层优化。
上述研究都是针对水平轴风力机叶片进行,但垂直轴风力机凭借气动性能良好、结构简单、成本较低、便于安装等优点一直是研究的热点。尚彬彬[21]建立了一种H型垂直轴风力机叶片桁架结构模型,并优化内部框架结构及蒙皮铺层。徐秩[22]根据剖面剪流理论优化了H 型垂直轴风力机叶片的腹板位置,并应用遗传算法对优化后的叶片进行铺层顺序及厚度的优化。然而,目前对于考虑时变载荷效应的叶片结构优化并未涉及。本文应用解析法和有限元法研究构件发生弯曲变形时的结构特性,建立采用有弯度尖尾缘翼型的H 型垂直轴风力机叶片有限元模型;利用FLUENT 计算叶片表面瞬态压力分布,基于FSI 映射方法提取实时变化的气动力;对粒子群算法进行改进,采用改进的算法对多种荷载耦合作用时叶片的结构参数和材料铺层进行多目标优化设计。
1 弯曲构件结构性能的理论与有限元分析
H 型垂直轴风力机复合材料叶片的约束和受力与外伸梁类似,且层合板是复合材料的基本构造形式。因此,通过层合板理论和Tsai-Wu 强度准则[16]求出外伸梁弯曲变形下各层的应力分量和强度比,并与有限元结果比较分析。
1.1 应力分量和强度比计算
复合材料层合板第g 层偏轴应力应变关系式为
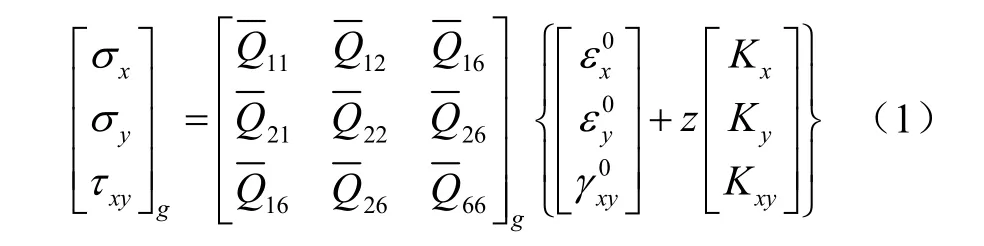

式中N、M 为层合板横截面单位长度所受的内力、内力矩,N/mm、N;A、B、D 分别为面内、耦合、弯曲的刚度矩阵,N/mm、N、N·mm。
利用坐标转换得到纤维向正轴应力分量为

式中 σ1、σ2为正轴正应力,MPa;τ12为正轴剪应力,MPa;m = cosα , n= sin α,α 为偏轴与正轴之间的夹角,rad。
根据Tsai-Wu 强度准则,强度比R 表达式为

1.2 梁弯曲变形的理论与有限元分析
建立20 mm×4 mm×2 mm 的长方体梁几何模型(图 1a),采用单轴向玻璃布进行0°、90°、90°、0°的铺层[10],各层厚度均为0.5 mm。梁受到绕X 轴的内力矩而发生弯曲时,式(2)左端的内力矩只有Mx,其余量均为0,取Mx=20 N·mm。将材料强度参数代入式(3)和(4),计算得到应力分量和强度比的解析解。同时,建立该梁的有限元模型,约束X=5 mm、15 mm 处节点的自由度,耦合X=20 mm 处Y 方向的转动位移以避免层间出现剪切力,施加绕X 轴的内力矩Mx=20 N·mm(图 1b),对模型进行静力分析得到应力分量和强度比的有限元解。解析法与有限元法的结果如表1,比较分析可知横向、纵向、剪切应力以及强度比的平均误差分别为 0.002 4%、0.000 2%、0、0.000 3%,表明ANSYS 建模过程中铺层和约束方法以及仿真结果的正确性。
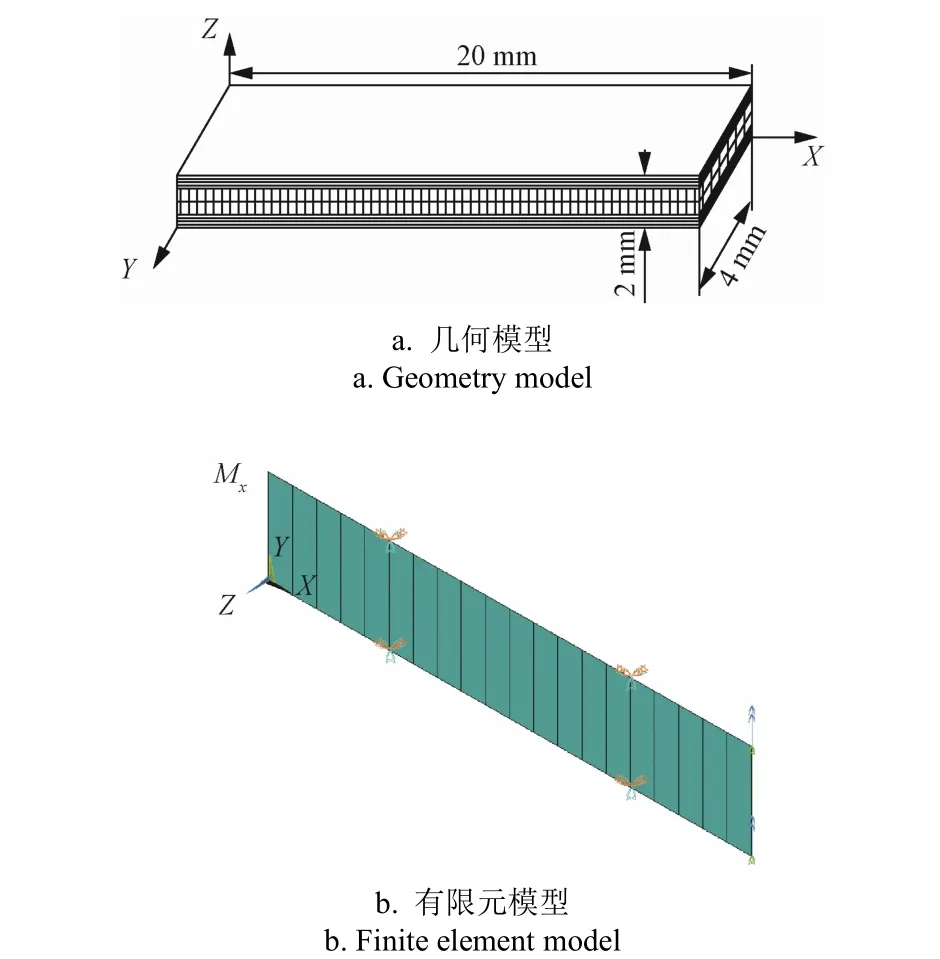
图1 梁的几何模型和有限元模型 Fig.1 Geometry model and finite element model of beam

表1 梁弯曲变形下应力分量和强度比的解析解和 有限元解 Table 1 Analytical and finite element results of stress component and strength ratio of beam under the bending deformation
2 FSI 映射气动载荷计算
准确、实时获得气动力对叶片的结构特性分析至关重要,且考虑弯度效应的NACA0021 翼型尖尾缘改型能提高叶片的气动性能。因此,构建有弯度的尖尾缘翼型,利用FLUENT 计算新翼型叶片的表面压力,并基于FSI(Fluid Structure Interaction)映射方法提取气动力。
2.1 研究对象
应用气动设计理论对采用NACA0021 翼型的100 W H 型垂直轴风力机3 叶片风轮进行几何尺寸设计,基本参数如下[23]:额定风速v=7 m/s,额定转速n=200 r/min,尖速比λ=1.777,风轮直径d=1.188 929 112 m,叶片长度l=1.307 822 023 m,翼型弦长c=0.313 503 278 m。利用坐标旋转变换和缩放横纵坐标系数进行NACA0021 改型(图2a),得到尖尾缘翼型NACA0021S,并使翼型中弧线位于风轮圆周上,获得有弯度的翼型NACA0021SC(图 2b)。
原翼型某控制点T 的横、纵坐标kx 和ky 为
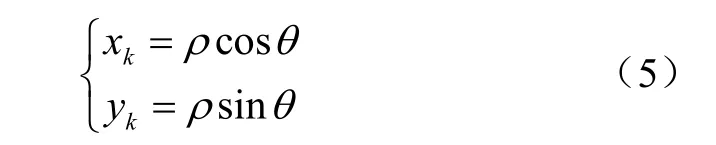
式中ρ 为OT 的长度,m;θ 为OT 与x 轴的夹角,rad;k= 1,2,分别表示上、下翼面。

图2 翼型的改型与增加弯度图 Fig.2 Modification and increasing camber for airfoil
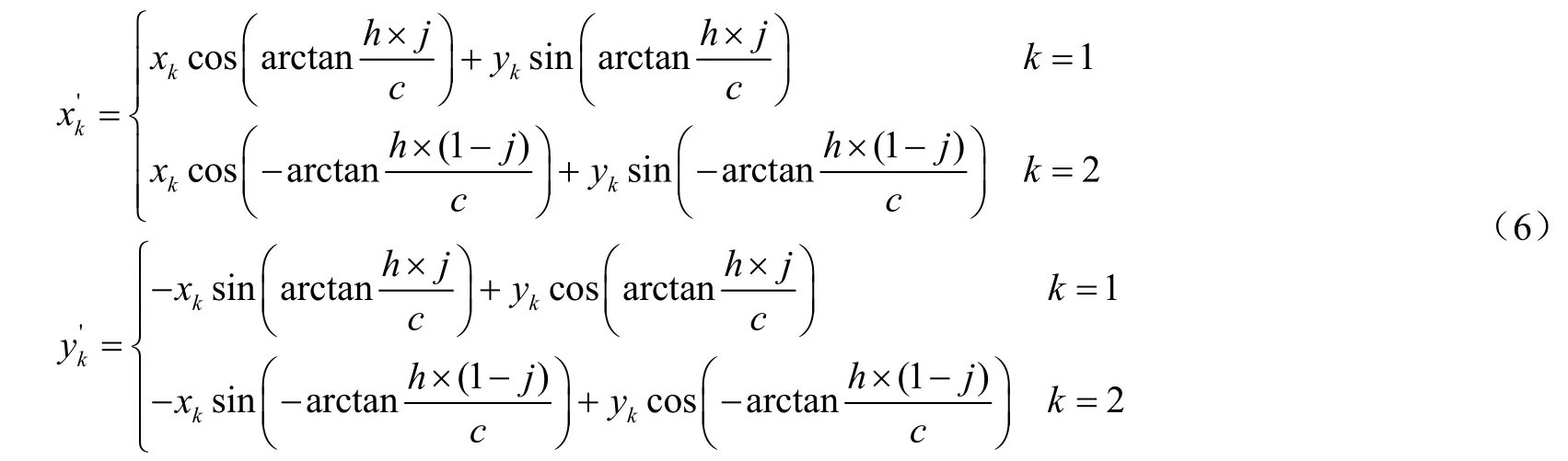
式中h 为尾缘厚度,m; j 为上翼面尾缘厚度与钝尾缘厚度的比值;c 为翼型弦长,m。
为保证改型后翼型的弦长、最大相对厚度及位置不变,将上、下翼面旋转后的横坐标分别乘以cosβ 和cosφ,纵坐标分别减去和加上,获得尖尾缘翼型坐标

2.2 数值计算模型
采用GAMBIT 软件生成风轮的几何模型、计算域及网格。计算域由2 个静域和1 个旋转域组成(图3a),静域1 是直径为d-3c 的圆柱体1,静域2 是22d×10d×l的长方体和直径为d+3c 的圆柱体2 之间的区域,旋转域是圆柱体1 和2 之间的区域,各区域的长度均为l。风轮的旋转中心O1距离计算域的左、前、上边界分别为10d、5d、0.5l,3 个翼型的气动中心均位于风轮的圆周上,相邻气动中心之间的中心角为120°。
旋转域中叶片顶端面翼型线段JI 和IJ 均按照双向连续增长率为1.02 的方式布置150 个节点,利用同样的方式处理其他两个叶片;2 个静域中线段AB、BC、CD、DA 以及内外圆周分别均匀布置50、20、50、20、80、120个节点;采用共10 层的边界层进行翼型近壁面加密,首层网格高度为0.000 2 m,增长率为1,由内向外划分;定义2 个尺寸函数,进行旋转域加密和静域2 稀疏处理。采用非结构三角形网格进行上表面网格离散化,通过扫略命令生成体网格(图3b、3c)。计算域的左、右两侧面分别为速度进流和压力出流边界,静域2 的前、后、上、下面和静域1 的上、下面均采用对称边界,旋转域的上、下面和叶片表面均为动壁无滑移边界条件,静域和旋转域之间用interface 定义连接。

图3 风轮的计算域及网格 Fig.3 Computational domain and mesh of wind wheel
在FLUENT 中,采用Realizable k-ε 湍流模型,压力和速度耦合方程采用SIMPLE 算法,各方程离散处理均采用二阶迎风格式[24]。入口额定风速为7 m/s,出口压力为零。为确保数值计算充分收敛,相邻周期内扭矩系数的偏差小于1%,连续分量、速度分量、k 和ε 的收敛准则均为10-5。
2.3 网格无关性和适应性
以文献[25]中的3 叶片H 型垂直轴风力机为例,当旋转域尺寸函数增长率分别取1.15、1.20、1.30,即网格数分别为3 565 920、2 918 720、2 346 400 时,计算扭矩系数 Cm。根据风能利用率,获得尖速比λ 为2.70 时风轮的瞬态及平均 CP值,并与试验结果比较分析(图 4a)。由图4a 可知,3 种网格数下, CP的瞬态值具有相同的周期性变化规律,在角度为90°、210°、331°位置附近最大,31°、151°、270°位置附近最小;CP的平均值分别为0.352 47、0.343 47、0.320 07,并随着网格数减少而减小,且网格数为2 346 400 时计算结果最接近试验值0.300 67。因此,选择2 346 400网格数计算不同尖速比下风轮的 CP平均值(图4b)。由图4b 可知,数值和试验结果均随着尖速比增大而先增后减,大部分λ 下误差在10%以内。由于数值计算忽略了垂直轴风力机的支撑结构和气动弹性的影响,且湍流模型无法提供自然的湍流粘度,故两者存在一定的误差。
2.4 FSI 映射方法加载气动力
FSI 映射方法的步骤为:利用FLUENT 软件计算叶片表面压力分布,通过FSI Mapping-surface 命令读取任意瞬时的有限元模型信息,并与FLUENT 中的信息匹配,进而映射气动力转换成APDL 语言,得到输出文件。在ANSYS 软件中读取该文件,将气动力加载在网格单元上,实现FLUENT 和ANSYS 间的实时压力传递。
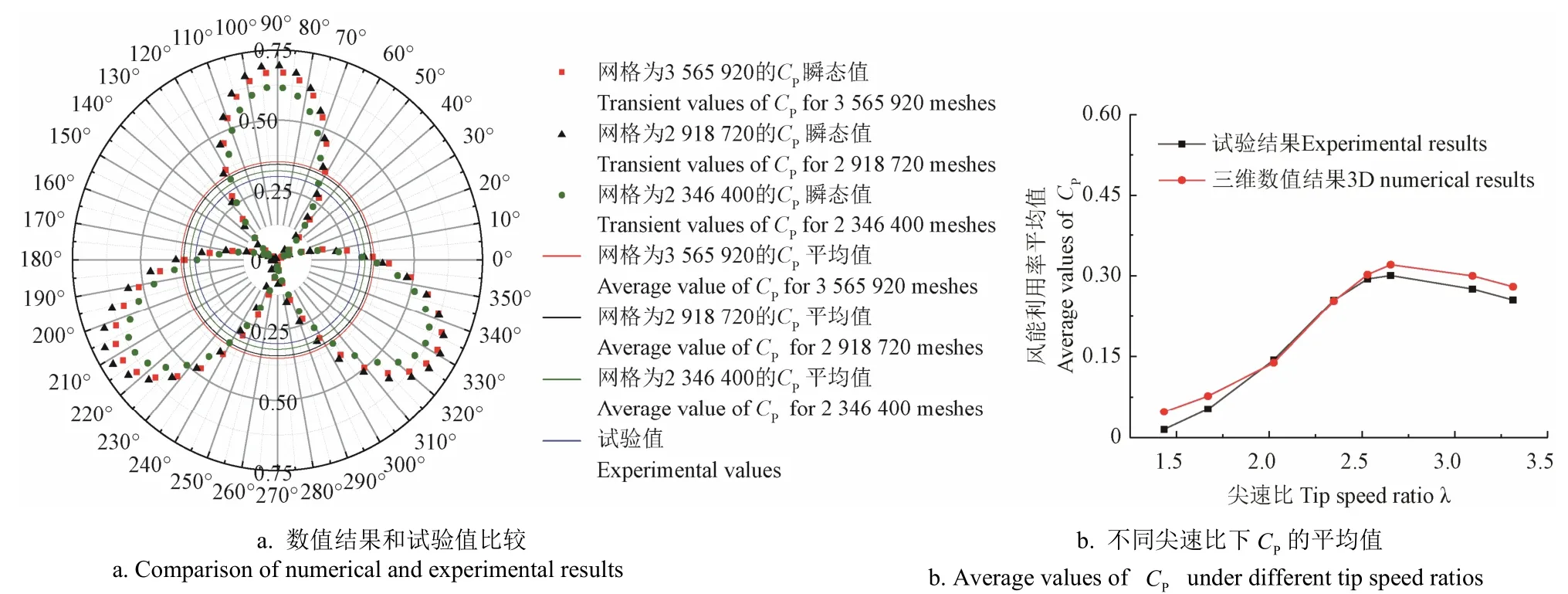
图4 网格无关性及适应性验证 Fig.4 Verification of mesh independence and adaptability
3 叶片有限元模型
叶片的截面结构如图5a 所示,采用ANSYS 软件建立叶片的几何模型并进行复合材料铺层。铺层材料选用单轴向玻璃布、双轴向玻璃布、三轴向玻璃布、胶衣布和泡沫[14],分别用UT、BT、TT、FT、GT 表示。根据铺层规则[22],叶片的前缘、主梁、尾缘、腹板的初始铺层顺序及层数分别为 FT+TT+3UT+TT、FT+TT+BT+ 3UT+BT+TT、FT+TT+3UT+GT、2BT+GT+2BT,铺层角度均为0°,叶片质量为2.50 kg,网格划分如图5b所示。90°方位角下叶片的表面压力分布如图6a 所示,基于FSI 映射方法获得气动力,通过ACEL 命令定义重力加速度 9.80 m/s2、OMEG 命令定义角速度20.93 rad/s,以施加重力和离心力,如图 6b 所示。
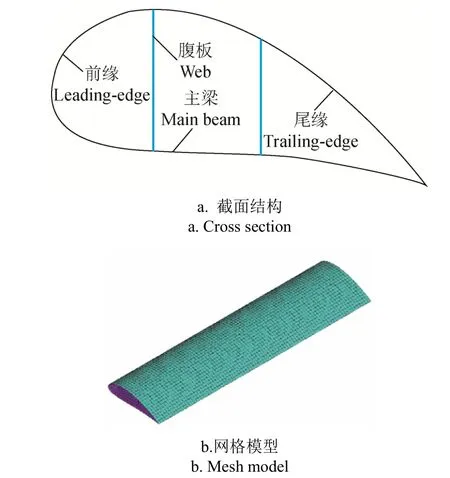
图5 叶片的截面结构及网格模型 Fig.5 Cross section and mesh model of blade
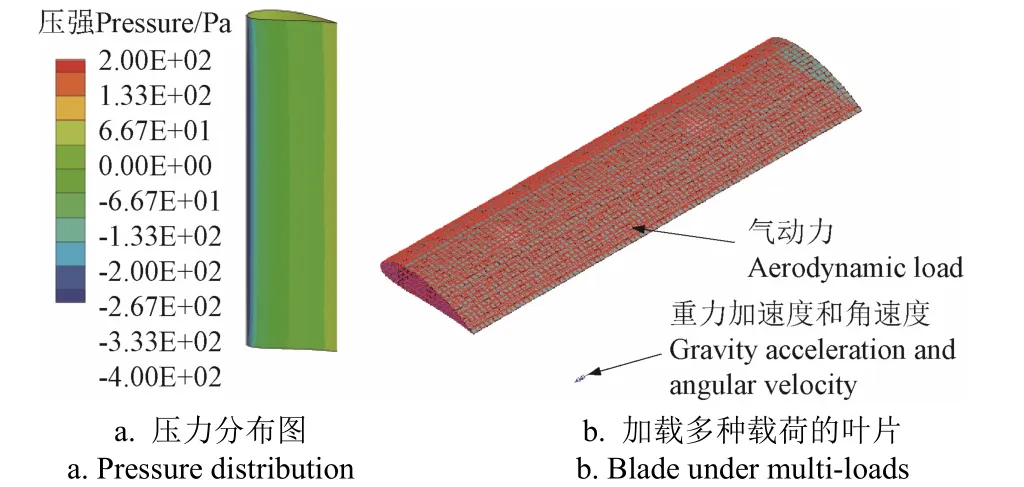
图6 叶片表面的重力、离心力和气动力力 Fig.6 Gravity, centrifugal force and aerodynamic load on the blade surface
4 优化模型建立
4.1 目标函数
高强度和轻量化是小型H 型垂直轴风力机叶片的发展方向[11]。因此,以叶片的总质量最小和层合板强度比最大值最大为设计目标

式中X 为优化变量; mblade为叶片质量,kg;R 为强度比;λ1、 λ2为权值系数,。
4.2 优化变量
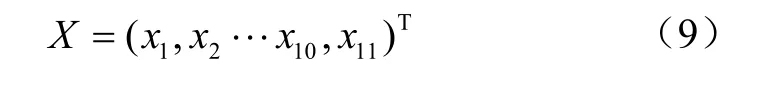
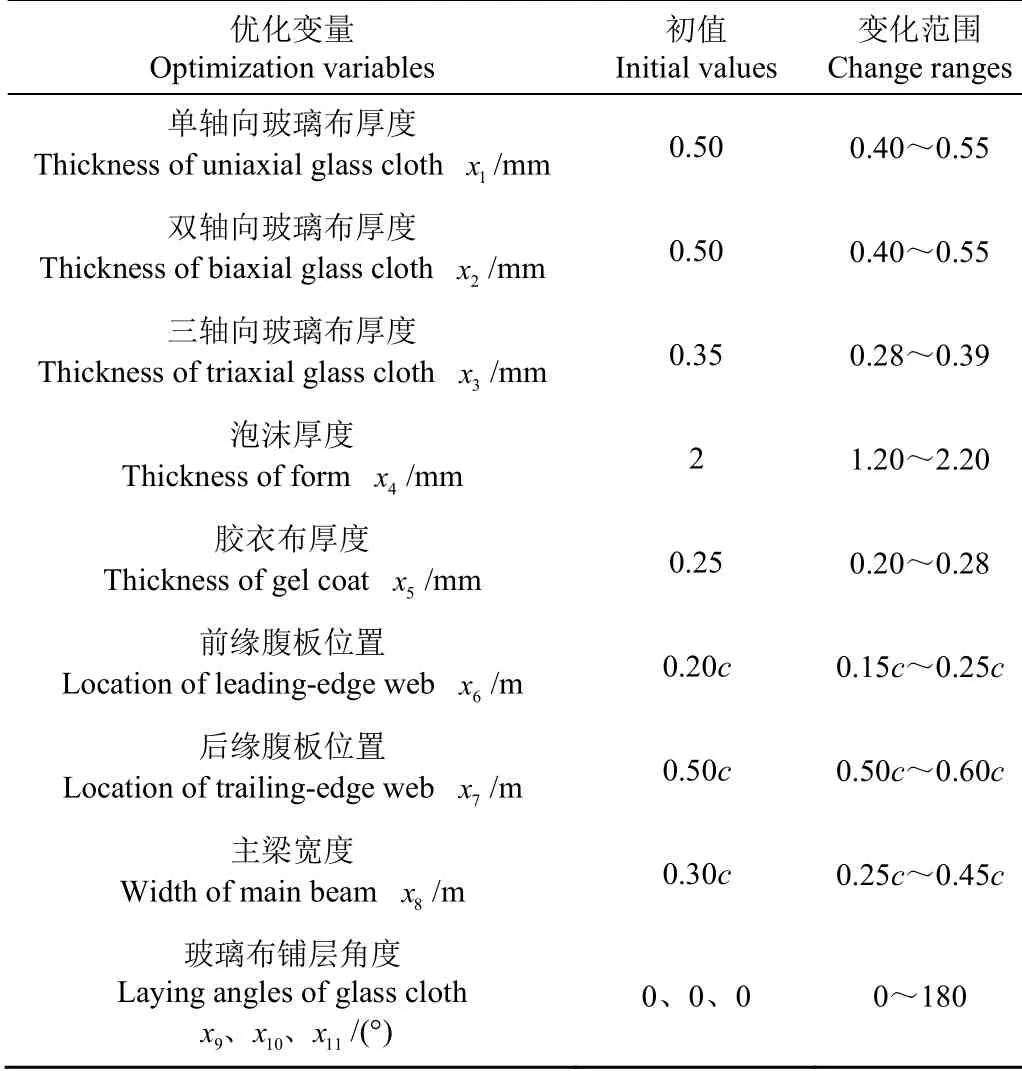
表2 优化变量的初值及变化范围 Table 2 Initial values and change ranges of optimal variables
4.3 约束条件
叶片与叶臂连接处容易产生应力集中,应使优化后叶片的最大应力值σmax 小于初始最大应力值σ0、最大变形量maxd 小于初始最大变形量 d0

4.4 改进粒子群算法
粒子群算法具有全局寻优、程序简单且易实现、精度高等优点,但局部寻优能力和稳定性差。学习因子 c1、能使粒子避免陷入局部极值,而惯性权重w 的引入可加大粒子的搜索范围并提高全局寻优能力。w 和 c1、 c2的稳定性条件为[26]
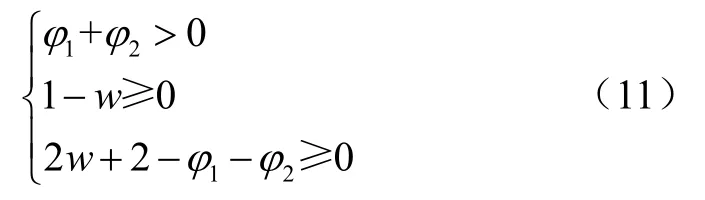
基于此,通过惯性权重余弦自适应和学习因子动态调整来改进粒子群算法,w 和 c1、 c2的表达式为

式中,t 为当前迭代次数,maxt 为最大迭代次数。
将改进的粒子群算法与有限元法相结合,进行多种载荷耦合下100 W H 型垂直轴风力机叶片的结构优化设计,流程图如图7 所示。粒子群算法参数为:种群数量为20,变量维数为11,最大迭代次数为200。
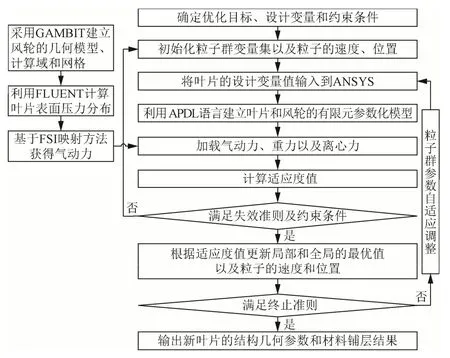
图7 叶片结构优化设计流程图 Fig.7 Flow chart of the blade structure optimization design
5 计算结果及分析
分别针对90°、180°、270°、360°方位角下单叶片以及风轮进行气动力、重力和离心力耦合作用下多目标结构优化,研究优化前后叶片的质量、应力、应变、位移、强度比倒数的变化规律。以90°方位角下单叶片优化为例,迭代历程如图8 所示。可以看出,当迭代到80 次时,目标函数已趋于收敛且优化效果明显。表3 为单叶片位于不同方位角时以及风轮的优化结果。
5.1 单叶片优化结果分析
将优化结果带入叶片的参数化模型并进行静力分析,如图9 所示。可以看出,单叶片在90°、180°、270°、360°方位角下优化后质量减小程度不同,分别为13.70%,11.85%,8.09%,9.60%;最大应力和应变在各方位角下均有很大程度降低,且分别在90°和180°方位角时降幅最大,为20.71%和23.77%;最大位移的降幅在360°方位角时最大,90°方位角时次之,分别为9.34%和6.58%,其余方位角下变化很小;强度比倒数的降幅在180°方位角下达到9.38%,270°、360°方位角下均不到5%。这些说明叶片的应力集中现象减弱,应变和变形减小,强度增大,结构性能提高。
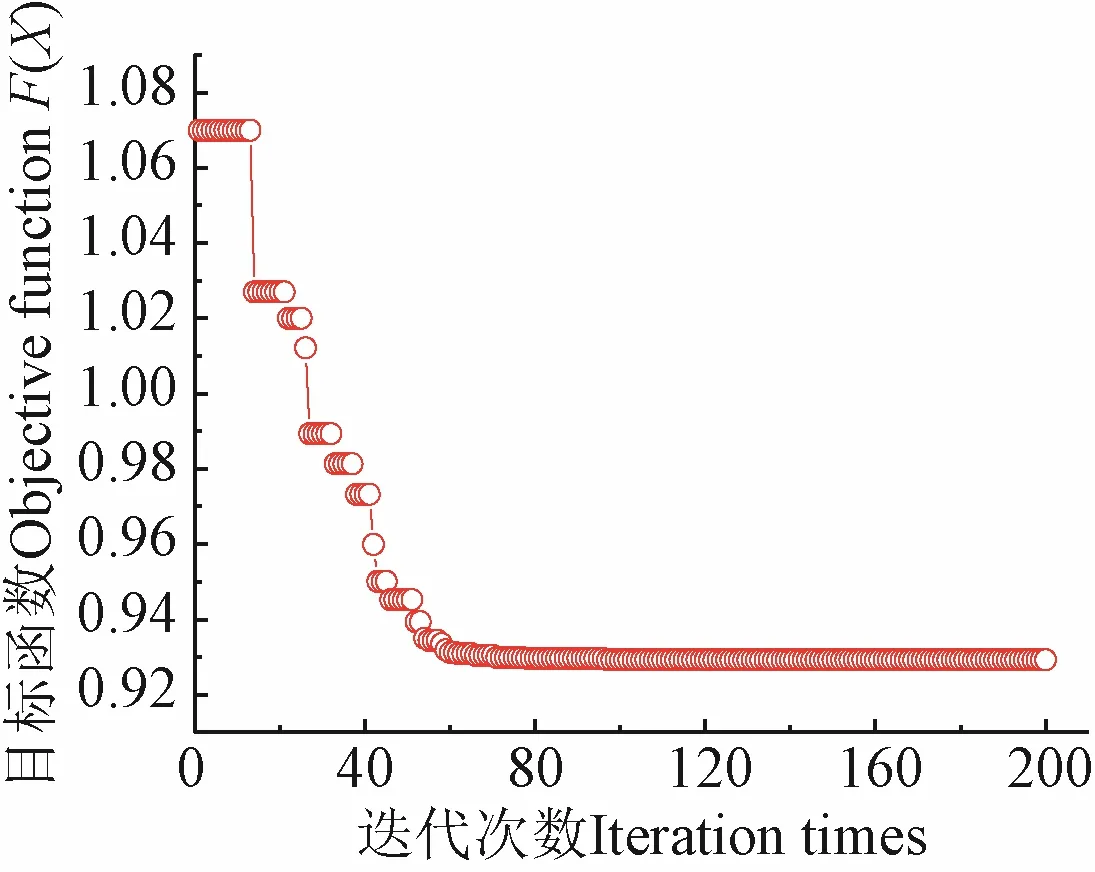
图8 90°方位角下单叶片的结构优化迭代历程 Fig.8 Iteration process of the single blade structure optimization at the 90° azimuth

表3 单叶片位于不同方位角时以及风轮的优化结果 Table 3 Optimization results of single blade at different azimuth and wind wheel
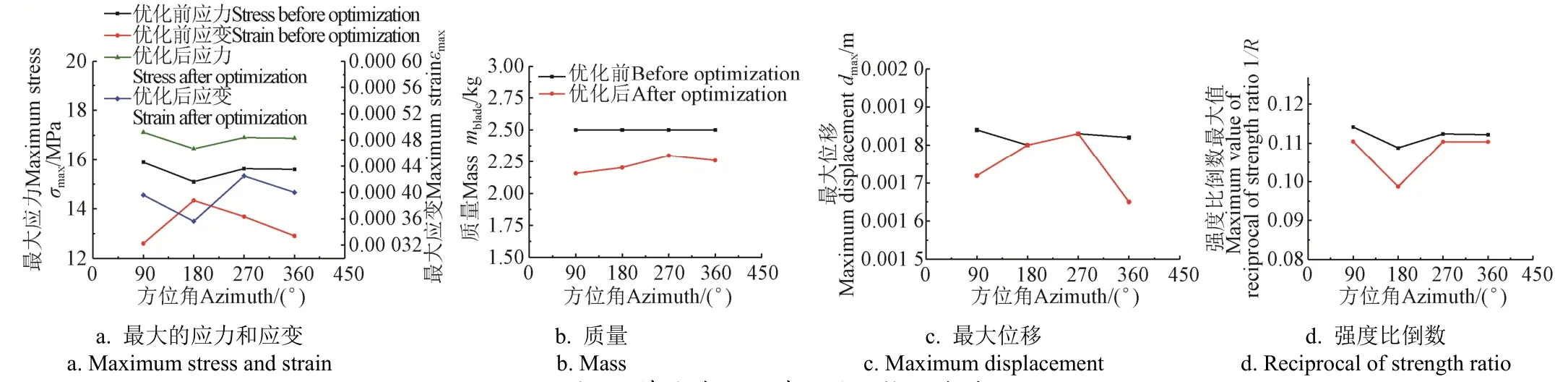
图9 单叶片优化前后的结构性能对比 Fig.9 Structural performance comparison of single blade before and after optimization
5.2 风轮优化结果分析
对采用优化后参数构建的风轮进行静力分析和结构性能对比,如图 10 和图11 所示。风轮优化后的质量为6.94 kg,相比优化前的7.50 kg 减小了7.51%。由图10可知,优化后风轮的最大位移略有减小,为1.90%,但分布规律一致;最大应力和应变仍出现在叶片与叶臂的连接处,分别减小8.50%和20.20%,应力集中现象减弱。由图 11可知,叶片1(90º方位)的应力、应变和位移的最大值在风轮优化前后均最大,叶片3(330º方位)次之,叶片2(210º方位)最小。风轮优化后,叶片1、2、3 的应力最大值分别减小8.50%、9.16%、8.76%;应变最大值的降幅均很大,分别为20.20%、20.48%、20.46%;位移最大值均略有减小,分别为1.97%、2.40%、2.26%;强度比倒数最大值分别减小16.11%、16.55%、16.33%。这些说明各叶片的强度均有不同程度地提高,风轮抵抗变形和破坏的能力增强。

图10 风轮优化前后的位移、应力分量和应变分量 Fig.10 Displacement, stress component and strain component before and after the wind wheel optimization

图11 风轮优化前后各叶片的结构性能对比 Fig.11 Structural performance comparison of each blade before and after the wind wheel optimization
6 结 论
1)采用FLUENT 软件计算叶片表面的压力分布,通过FSI 映射方法获得气动力并施加在结构的网格单元上,实现了FLUENT 和ANSYS 间气动力的传递。
2)利用学习因子动态调整和惯性权重余弦自适应改进了粒子群算法。
3)90°、180°、270°、360°方位角下单叶片以及风轮在进行多种荷载耦合作用下的多目标结构优化后,单叶片在各方位角下质量分别减小13.70%、11.85%、8.09%、9.60%,最大应力和最大应变的降幅分别在90°和180°方位角下高达20.71%和23.77%,最大位移的降幅在90°和360°方位角下较大且为6.58%和9.34%,强度比倒数在180°方位角下减小最多且为9.38%;风轮的质量减小7.51%,最大的应力和应变分别减小8.50%和20.20%,最大位移仅减小1.90%,强度比倒数的最大值减小16.11%,即应力集中现象减弱,变形减小,强度增大,从而使结构性能增强。

