基于任务分配和数据集副本的科学工作流数据布局
尚 蕾,刘茜萍
(南京邮电大学 计算机学院 江苏省大数据安全与智能处理重点实验室,南京 210023)
0 概述
工作流是对工作流程及其各操作步骤之间业务规则的抽象、概括与描述[1]。近年来,随着信息技术不断发展,天文学[2]、高能物理学[3-4]以及生物信息学[5]等研究领域需要处理的数据量呈爆炸式增长,科学工作流(Scientific Workflow,SW)应运而生。科学工作流是一种面向海量密集型数据流、以减少计算成本为目标的应用系统,可提升科学实验过程的自动化程度,降低资源消耗。但科学工作流任务的数据量较为庞大,执行费用高,常规计算平台环境难以满足其需求。而云计算采用按需使用付费模式,使用户能以更低廉的价格获取计算资源和存储资源,并提供互联网模式使研究者更方便地进行资源分享和任务合作,为科学工作流的高效运行提供了较为理想的平台环境。
然而,云环境下科学工作流的运行面临诸多挑战[6],最主要的问题之一是数据布局。科学工作流数据布局本质上是一种带有最大完成时间[7]和费用[8]等约束条件的NP难问题。首先,云数据中心分布在世界各地,例如亚马逊EC2云服务在美国、日本等地拥有40多个数据中心,导致科学工作流运行时需要跨数据中心进行数据存储与传输,增加了数据传输费用。此外,若数据集中存储在一个云数据中心,将导致此中心的存取、复制、备份与分析工作量过大,影响工作流执行的整体效率[9-10],因此需要在数据中心实现负载均衡。对此,已有研究者提出了多种数据布局解决方案。文献[11]提出一种根据K均值算法对数据集依赖矩阵进行划分的数据布局方法。文献[12]提出一种基于遗传算法的3阶段数据布局方法。文献[13]提出一种基于粒子群算法的工作流数据布局方法,将依赖度高的数据集尽量放在同一数据中心。文献[14]提出一种BDAP方法。文献[15]提出一种两阶段数据放置方法,初始阶段对数据集进行聚类分配,中间阶段重新动态分配数据集。文献[16]提出一种云环境下基于整数线性编程模型的数据放置算法。文献[17]提出一种基于图区分的数据布局方法,减少了跨数据中心数据传输费用。文献[18]提出一种基于遗传算法算子的自适应离散粒子群优化算法。文献[19]提出一种多目标优化的数据布局策略,先对固定数据集布局,再对非固定数据集进行分配。文献[20]提出一种基于粒子群算法的工作流层的数据布局方法。但在以上方法中,文献[11-13]并未考虑任务分配的不同结果对数据传输费用产生的影响,文献[14,20]考虑了数据集副本问题,但并不是针对减少整体数据传输费用,不能从本质上解决整体数据传输费用问题,文献[18]未考虑科学工作流数据阶段布局问题。
本文提出基于任务布局和数据集副本建立的云环境下两阶段科学工作流数据布局方案。该方案以减少数据传输费用为主要目标,同时尽可能地兼顾数据中心负载均衡。
1 问题描述
科学工作流是一种数据密集型应用程序,任务和数据集之间是多对多的关系,任务和任务之间存在着非常强的依赖关系。此外,任务和任务之间还有着时序上的先后关系,只有当一个任务的前驱任务全部执行完毕时,该任务才能执行。
定义1(科学工作流) 科学工作流(SW)可以定义为三元组
定义2(任务ti)ti定义为四元组
定义3(数据中心) 数据中心集合定义为DC,单个数据中心dcv定义为二元组
科学工作流数据中的数据集拥有多重属性,可以根据数据集放置位置是否固定分为固定数据集和灵活数据集;也可以根据数据集是否被至少两个任务使用,分为共享数据集和非共享数据集。本文数据集产生后不会被修改,可以直接进行使用,下文是关于科学工作流中数据集相关概念的定义。
定义4(数据集) 数据集dp定义为四元组
在科学工作流中,任务与数据集紧密相关,一个任务可以与多个数据集相关,一个数据集也可以与多个任务相关。研究数据布局问题可以从任务布局着手,研究任务与数据集之间的关系来优化解决数据布局的相关问题。本文采用数据费用开销来衡量数据布局结果的好坏,表示为Cost;数据费用开销包括数据传输和数据集存储两部分费用开销。数据传输费用表示为DTCost(dp),其值为数据集大小与传输单价的乘积;数据集存储费用表示为DSCost(dp),其值为该数据集的存储时间与存储单价的乘积,数据费用开销越小,则说明该布局方案结果越好。此外,考虑到科学工作流中经常涉及同一个数据集需要在多个数据中心之间传输,可以设置数据集副本,通过增加数据集副本的存储费用来减少整体传输的费用消耗,而本文以增加数据集存储费用来减少数据集传输费用以达到降低总费用的效果,因此,本文数据集存储费用开销指数据集副本存储开销。下文依次给出任务布局、数据集副本和数据布局的相关定义。
定义5(任务布局方案) 工作流的一个任务布局(Task Layout,TL)方案是从任务集合T到数据中心集合DC的一个映射,对于∀ti∈T,∃dcv∈DC与之对应,i=1,2,…,n,v=1,2,…,l,表示为:
TL=∪i=1,2,…,n{ti→dcv}
即TL(ti)为任务布局方案TL中任务ti所对应的数据中心。
定义6(数据集副本rq)rq定义为二元组
定义7(数据布局方案) 工作流的一个数据布局(Data Layout,DL)方案是从数据集集合DS和数据集副本集合R到数据中心集合DC的一个映射,对于∀dp∈DS,∃dcv,dcu∈DC与之对应,p,q=1,2,…,m,v=1,2,…,l,表示为:
即DL(dp)为数据布局方案DL中数据集dp所对应的数据中心,DL(rq)为数据布局方案DL中副本集rq所对应的数据中心。本文云环境下科学工作流的数据布局由运行前所得布局方案DLinit和运行中布局方案DLgen两部分组成。
2 任务分配
给定一个涉及n个任务和m个数据集的科学工作流,以及可存放数据集和执行任务的l个数据中心,本文在实现任务分配的基础上解决云环境下科学工作流的数据布局问题。科学工作流中数据集与任务之间存在着密不可分的依赖关系,而这些关系在工作流设计之初便已经存在,基于此,本文将任务分配纳入数据集布局方法考虑中。本文中任务的分配基于数据集与任务的依赖关系,即依据这些依赖关系再进行任务之间依赖度的定量计算,根据计算结果得到相应的任务分配结果。
2.1 任务依赖矩阵
本文提出的任务依赖度为任务之间相关数据集大小之和而不是相关数据集个数,简单工作流示例如图1所示。

图1 简单工作流示例
在图1中,t1的输入数据集为{d1,d2},输出数据集为{d3},t2的输入数据集为{d2,d3,d5,d6},输出数据集为{d4},t3的输入数据集为{d4,d5,d6},输出数据集为{d7},各数据集大小如表1所示。

表1 数据集大小
此时,t1与t2之间相关数据集个数为2,t2与t3之间相关数据集个数为3,若按相关数据集个数来计算,那么t2与t3之间存在着最高的依赖度,若将t2与t3分配至同一个数据中心dc1,t1位于另一个数据中心dc2,则此时需要从dc2传输数据集d2与数据集d3至dc1,传输的数据总量为11 GB。而若是按照两个任务之间相关数据集的大小之和定义其依赖度,则t2应与t1具有最高的依赖度,应将t1与t2分配至同一个数据中心dc1,t3位于另一个数据中心dc2,此时需要从dc1传输数据集d4、d5和d6至dc2,传输的数据总量为3 GB。为尽可能降低这种影响,本文提出任务依赖度的定量计算方法,任务之间的依赖度为任务之间共同关联数据集的大小之和,下文给出本文中任务依赖度的定义。
定义8(任务依赖矩阵) 任务依赖矩阵(Task Dependency Matrix,TDM)表示所有任务之间的依赖度,本文将任务与任务自身的依赖度设置为0,即任务依赖矩阵是一个n×n的对角线为0的对称矩阵,n是任务的个数,tdmij是ti和tj之间的任务依赖度,表示为:
(1)
CD=(ti.ID∪tj.OD)∩(tj.ID∪tj.OD),
i,j=1,2,…,n,i≠j
其中,ti.ID表示任务ti的输入数据集集合,ti.OD表示任务ti的输出数据集集合,ti.ID∪tj.OD表示与任务ti相关的数据集集合,CD表示同时与任务ti和tj相关数据集集合。
2.2 基于定量计算任务依赖度的任务布局方法
本文任务布局的目的在于将所有任务分配至适合的数据中心,为之后的数据集分配奠定基础。本文按照任务起始时间对n个任务进行排序,分为固定任务分配、起止时间计算、任务依赖度计算、非固定任务分配4个步骤(本文中研究的科学工作流只有唯一的一个起始任务,并假设为t1):
步骤1将固定任务分配至相应数据中心
输入数据集DS,数据中心DC,任务集T
输出灵活数据集Tfix,当前任务布局TL
1.for each dpin DS:
2.if dp.fix != 0:
3.allocate(dp.preT∪dp.sucT)to dcfix
4.update TL
5.Tfix←Tfix+(dp.preT∪dp.sucT)
该方法主要是分配固定任务,时间复杂度为O(m),固定任务被定义为与固定数据集相关的任务,即固定数据集的前驱任务和后继任务均为固定任务,考虑到固定数据集无法移动,与之相关的任务都需要在其所在数据中心执行。科学工作流任务执行的前提是所有的输入数据集都传输到同一个数据中心,而固定数据集不可移动,故本文中不考虑同一个任务需要使用位于不同数据中心的多个数据集的情况。
步骤2根据式(2)计算各个任务的起止时间
输入任务集T
输出任务的起止时间ti.st和ti.et
1.for each tiin T
2.ti.st←0
3.if i=1:
4.ti.et←ti.ext
5.else:
6.for each tjin ti.FT
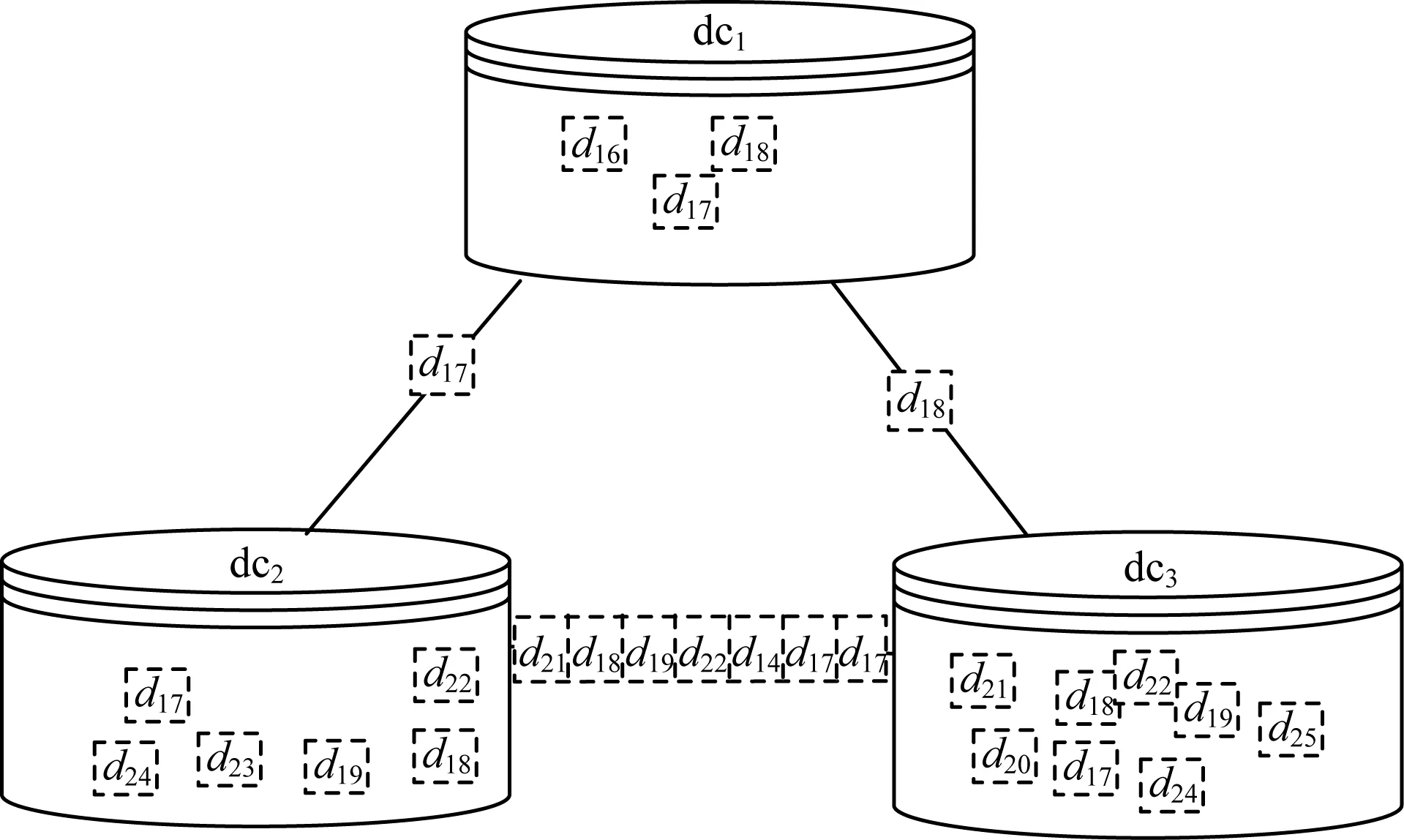
7.if ti.st 8.ti.st←tj.et 9.ti.et←ti.st+ti.ext//calculate the starting time and //ending time of tasks 该方法主要是计算任务起止时间,时间复杂度为O(n2)。一个任务的开始时间取决于其前驱任务的最晚执行时间,而结束时间为开始时间与执行时间之和,因此起止时间可由下式计算得出(t1为初始任务): (2) ti.et=ti.st+ti.ext,i=1,2,…,n 其中,ti.st表示任务ti的开始时间,tj.et表示任务tj的结束时间,ti.FT表示任务ti的前驱任务集合。 步骤3计算任务依赖度 输入数据集DS,任务集T,数据中心DC 输出任务依赖矩阵TDM 1.for each tito n in T: 2.for j to i: 3.tdmij=0 4.while(ti!=tj): 5.CD=(ti.ID∪ti.OD)∩(tj.ID∪tj.OD) 6.if CD !=∅: 7.for each dpin CD: 8.tdmij=tdmji=dp.ds+tdmij//build TDM 该方法主要计算任务之间的依赖度,算法时间复杂度为O(n3),主要依据2.1节中的任务依赖度的计算式(1)。每两个任务都会有一个共同数据集集合,集合中数据集大小之和即为两个任务之间的依赖度,依赖度数值越大,两个任务关系更为紧密。 步骤4分配非固定任务 输入灵活任务集Tfix,数据中心DC 输出任务布局方案TL 1.sort tiin Tfix according to ti.st//sort the tasks by //starting time 2.Tflex←T-Tfix 3.while Tflex: 4.aven←|Tflex|/|DC| 5.for each tiin Tfix: 6.S←{ti} 7.Denp←0 8.while |S-ti| 9.for each tjin Tflex: 10.for each tkin S: 11.Denp←denp+tdmjk 12.find the max denp 13.add tjinto S 14.allocate tjto ti.dc 15.update TL 16.delete tjin S from Tflex//allocate flexiable tasks 17.return TL 该方法主要是利用已经分配完成的固定任务,完成非固定任务的分配,该算法时间复杂度为O(n3)。基于非固定任务可以分配在任何一个数据中心,然而分配在不同的数据中心上会导致后续数据集传输量存在不一样的结果的考虑,本文从非固定任务与固定任务的关系寻找突破口,首先将固定任务按照起始时间排序;接着将最早开始的固定任务所在的数据中心上的所有固定任务一起加入空集S中,依次计算该集合中任务与非固定任务之间的任务依赖度,寻找依赖度最高的非固定任务加入集合S,继续寻找与集合S中任务依赖度之和最高的任务,加入集合S,直到集合S里任务数量等于每个数据中心上的平均任务数量为止,然后删除非固定任务集Tflex中对应的已经分配完毕的非固定任务,如果非固定任务集合Tflex不为空集,则重复该阶段之前所有操作,直到任务完全分配结束。 在完成任务分配后,需要根据任务分配的结果,将工作流中涉及的m个数据集合理布局至l个数据中心。考虑到有些数据集需要被多个任务所使用,若这些任务分散在各个数据中心,则不可避免地需要将数据集进行多次传输,这无疑会增加数据集的传输总量,导致数据传输费用的上升,对于需要多次传输的数据集,本节将在相应的数据中心上建立数据集副本以达到降低数据传输量的目的。此外,考虑到有些数据集是工作流运行之前便已经存在,有些数据集是工作流运行之后才生成的,本节将数据布局分成工作流初始阶段和工作流运行阶段两个阶段完成。综上,本节主要任务是在兼顾负载均衡和任务执行时间的基础上,以第2节中的任务分配结果为基础,尽可能地以降低数据费用开销为主要目的,并提出一个两阶段的基于数据集副本的数据布局方法。下文分别给出费用计算公式、数据集副本建立条件、初始阶段数据布局方法和运行阶段数据布局方法。 本文假定所有数据集在任务执行之前传输到位,其传输时间可以忽略不计,且所有数据集在数据中心上的最后一个后继任务执行完毕时被删除。 数据中心的数据传输费用分为传出费用与传入费用,总费用与传输的数据总量正相关,传输的数据总量越大,传输费用越高,传输数据总量越小,传输费用越低,以亚马逊AWS亚太地区(https://aws.amazon.com/cn/pricing/?nc2=h_ql_p)(东京)为例,每月传入数据1 TB~499 TB,0.07美元/GB,每月传出数据1 TB~499 TB,0.141美元/GB。本文单个数据传输费用的目标函数为: DTCost(dp)=dp.ds×(up+dp), q=1,2,…,|DS| (3) 其中,dp.ds表示数据集dp的大小,up表示各数据中心的传出单价,dp表示各数据中心的传入单价,up和dp取值均为常数。 数据中心的存储费用通常按时间计费,存储时间越长,费用越高。考虑到云环境下可能存在一些异常导致数据集丢失的情况,本文正本数据集的存续时间为从其第一个后继任务开始执行到所有数据中心上的最后一个后继任务执行结束,这样无论在何种情况下,正本存储时间都是一定的,所以正本存储费用可直接假设为常数C,而副本数据集在其相应的数据中心上用完即删除,副本的存储费用是需要计算的。 下面给出本文单个数据集存储费用的目标函数: DSCost(dp)=dp.ds×(latest(sucT.et)- earliest(sucT.st))×dsp (4) 其中,dp.ds表示数据集dp的大小,earliest(sucT.st)表示数据集dp的后继任务的最早开始时间,latest(sucT.et)表示数据集dp的后继任务最晚结束时间,dsp表示单位时间单位容量的存储价格。 云环境下科学工作流的数据布局总费用为包括副本数据集在内的所有数据集的传输费用与存储费用之和,本文中数据总费用开销的目标函数为: (5) 初始阶段的数据集布局方法用于布局DSinit中的数据集,该方法基于第2节任务分配结果,以建立数据集副本的方法来减少数据总费用开销为主要目标,分为分配DSinit中灵活数据集和建立数据集副本两个步骤(默认固定数据集已经存在于对应的数据中心): 步骤1分配DSinit中的灵活数据集 输入数据集DSinit,任务布局方案TL,数据中心DC 输出数据布局方案DLinit 1.Sort tiaccording to ti.st 2.for each tiin T: 3.allocate ti.ID to ti.dc//allocate the flexiable datasets 该方法主要是分配DSinit中的灵活数据集,时间复杂度为O(n)。考虑到DSinit中的数据集在工作流运行之前便已经全部存在,可以从任务的角度来分配数据集,将任务按起始时间排序,起始时间早的任务可以优先选择需要用到的数据集,将需要用到的数据集分配至自己所在的数据中心。一般来说任务个数是小于数据集个数的,从遍历任务角度出发去分配数据集比从遍历数据集角度去分配数据集更能够降低时间复杂度。 步骤2建立数据集副本 输入数据集DSinit,任务布局方案TL,数据中心DC 输出数据布局方案DLinit 1.for each dpin DSinit: 2.if |dp.sucT|≥2: 3.for each dcvin DC: 4.if |dp.sucT|≥2 and dpnot in dcv: 5.calculate DTCost(dp) 6.calculate DSCost(dp) 7.if ((|dp.sucT|-1)×DTCost(dp)>DSCost(dp) 8.build dp’ replication rq 9.update dcv.aS 该方法主要是通过遍历数据集检查是否需要建立数据集副本,算法时间复杂度为O(ml),是否建立数据集副本,主要取决于以下两个条件: 1)|dp.sucT|≥2。 2)(|dp.sucT|-1)×DTCost(dp)-DSCost(dp)>0。 考虑到如果数据中心只有一个任务需要用到该数据集,那么无论是否建立副本都需要进行一次传输,此时建立副本没有意义,因此条件1)表示副本存在的条件为一个数据中心至少存在着两个任务需要使用该数据集;又考虑到如果数据集存储费用大于数据集的传输费用,那么做不到通过增加存储费用来降低传输费用这一目的,因此条件2)表明只有当数据集的存储费用小于其传输费用时,副本才会被建立并存储。 工作流运行阶段数据布局方法用于布局DSgen中数据集,基于第2节中任务分配结果,仍然以建立数据集副本的方法来减少数据总费用开销为主要目标。 下文给出运行阶段科学工作流数据布局步骤如下: 输入数据集DSgen,任务布局TL,数据中心DC,任务集T 输出数据布局方案DLgen 1.for each dpin DSgen: 2.calculate the earliest tiwhich is in dp.sucT 3.if dp.ds 4.allocate dpto TL(ti) 5.update dcv.aS 6.else: 7.calculate next tiwhich is in dp.sucT 8.skip to line 5 9.if |dp.sucT|≥2: 10.for each dcvin DC: 11.if |dp.sucT|≥2 and dp.ds≤dcv.aS and dpnot in dcv: 12.calculate DTCost(dp) and DSCost(dp) 13.if ((|dp.sucT|-1)*DTCost(dp)>DSCost(dp) 14.build dp’ replication rq 15.update dcv.aS 16.Return Dlgen 该方法考虑科学工作流执行过程中的动态性,从单个数据集的角度出发,去考虑数据集的分配以及数据集副本的建立,每生成一个数据集,便考虑该数据集应该分配的位置以及是否需要建立数据集副本,该方法时间复杂度为O(ml)。 该阶段数据布局思路为依次分配数据集并判断是否需要建立数据集副本,与初始阶段布局方法的不同之处主要有以下3点: 1)分配数据集的方法不同; 2)判断数据集是否需要建立副本的时间不同; 3)建立数据集副本的条件稍有不同。 对于第1)点,运行阶段在分配数据集时,由于数据集是实时生成的,数据集不能够由任务挑选数据集,只能依次被分配,默认分配至后继任务中最早执行的任务所在的数据中心。对于第2)点,初始阶段的方法中判断哪些副本需要被建立是在正本数据集分配完毕之后,而考虑到工作流运行阶段每生成一个数据集都需要被后续任务使用,因而运行阶段每分配一个数据集便需要进行一次判断,如果等所有数据集全部产生完毕再进行遍历,此时已经没有意义,当最后一个数据集生成时,整个工作流已经执行完毕。对于第3)点,运行阶段数据布局方法中建立副本的条件比初始阶段数据集副本建立条件多一个,即还需要判断当前数据中心可用容量dcv.aS是否大于当前数据集大小dp.ds,即需要满足dcv.aS>dp.ds,如果小于数据集大小,则不能建立副本。考虑数据中心容量的情况只是为了预防现实情况中的过载,尽管过载情况极少发生,然而还是有必要将此考虑在内。 图2是一个简单的工作流示例,它由10个任务t1~t10、15个初始数据集d1~d15和10个生成数据集d16~d25组成,其中,d1、d6和d9为固定数据集,分别放置于dc1、dc2和dc33个数据中心上,3个数据中心可用容量均为200 GB。假定各数据中心之间上行传输费用为0.15美元/GB,下行传输费用为0.1美元/GB,数据存储费用为每小时0.2美元/GB。各数据集大小如表2~表4所示。根据式(2)和表5、表6可得出各任务起止时间。 图2 工作流示例 表2 初始数据集 表3 数据集生成(预估大小) 表4 数据集生成(实际大小) 表5 任务执行时间 表6 各任务起止时间 由上述输入设置可以基于式(1)构造出以下任务关系依赖矩阵: 可以看出,总任务数10个,固定任务3个,非固定任务7个,数据中心3个,因此为一定程度上的负载均衡,每个数据中心应有总任务3个或4个,固定任务1个,非固定任务2个或者3个。又因为d1、d6和d9为固定数据集,分别放置于dc1、dc2和dc33个数据中心上,所以与数据集d1相关的任务t1应放置于数据中心dc1上,与数据集d6相关的任务t4应放置于数据中心dc2上,与数据集d9相关的任务t6应放置于数据中心dc3上。按照第2节中的思路,第一步将固定任务按起始时间排序,排序结果为:t1→t4→t6,即t1最先开始执行,t6最后执行;第二步将t1加入空集S中,S={t1},与t1依赖度最高的任务是t2,将t2加入集合S中,此时S={t1,t2},接着计算与t1和t2依赖度最高的任务,结果为t3,因此将t3加入S中,此时S={t1,t2,t3},将此3个任务分配至数据中心dc1上,删除Tflex中对应的任务,并将集合S置为空集。由于Tflex不为空集,因此循环第二步,将第二个开始执行的固定任务t4加入空集S中,此时,S={t4},与t4依赖度最高的任务是t8,将t8加入集合S中,此时S={t4,t8},接着计算与t4和t8依赖度最高的任务,结果为t9,将t9加入S中,此时S={t4,t8,t9},将此3个任务分配至数据中心dc2上,删除Tflex中对应的任务。由于此时只剩一个数据中心的任务没有分配,因此剩余所有任务均分配至数据中心dc3上。分配结果如图3所示。 图3 任务分配结果 从图3可以看出,任务t1、t2和t3位于数据中心dc1上,任务t8、t8和t9位于数据中心dc2上,其余4个任务位于数据中心dc3上。 首先将所有任务按起止时间排序,执行时间早的任务优先选择需要用到的数据集,将数据集分配至对应任务所在的数据中心,分配结果如图4所示。从图4可以看出,数据集d1、d2、d3、d4、d5和d7位于数据中心dc1上,数据集d6、d8、d10、d11、d12、d13和d15位于数据中心dc26上,其余数据集位于数据中心dc3上。 图4 初始阶段数据集分配结果 然后建立数据集副本,依据2.2节的数据集副本建立条件,在该阶段中,数据集d12位于数据中心dc2,而位于数据中心dc3上的t6和t7都需要用到该数据集,d12的少传的费用为3.75美元,d12的存储时间为1.5 h,纯存储费用为4.5美元,不需要建立副本。 因此最终初始阶段布局方案会有数据集d7从数据中心dc1传输到dc2;数据集d11、d12、d12和d15从数据中心dc2传输到dc3;数据集d2和数据集d5从数据中心dc1传输到dc3。 运行阶段每生成一个数据集,便判断其分配位置,分配结果如图5所示。 图5 运行阶段数据集分配结果 从图5可以看出,数据集d16位于数据中心dc1上,数据集d17、d22、和d23位于数据中心dc2上,数据集d18、d19、d20、d24和d25位于数据中心dc3上。 依据2.2节中的数据集副本建立条件,在该阶段中,数据集d17位于数据中心dc2上,而位于数据中心dc3上的t5、t6都需要用到该数据集,d17的单次传输费用为3美元,存储费用为2.4美元,因此需要建立数据集副本r1。 最终,运行阶段会有数据集d17从数据中心dc1传输到dc2;数据集d18从数据中心dc1传输到dc3;数据集d18、d21和d22从数据中心dc3传输到dc2;数据集d19、d24和d17的副本r1从数据中心dc2传输到dc3。 本文的比较方法为文献[20]中的方法,该方法以减少跨数据中心数据传输费用为目标,比较结果如图6、图7所示。 图6 初始阶段费用对比 图7 运行阶段费用对比 从图6、图7可以看出,在科学工作流初始阶段,使用本文方法传输费用为17.25美元,比较方法为23.5美元。副本存储费用本文为0美元,比较方法为0美元。本文方法传输费用与副本存储费用之和为17.25美元,比较方法为23.5美元,本文方法降低了6.25美元,对比方法要比本文方法多出36%的费用。图7为运行阶段两者费用的对比,利用本文方法数据集传输费用为22美元,比较方法传输费用为28美元。副本存储费用本文方法为2.4美元,比较方法副本存储为0美元,本文方法传输费用与副本存储费用之和为24.4美元,比较方法为28美元。运行阶段中本文降低了3.6美元的传输费用,对比方法比本文费用多出15%。 图8所示为本文方法与对比方法两阶段费用之和。可以看出,本文为41.65美元,对比方法为51.5美元,比本文方法多出24%的费用。 图8 两阶段费用之和对比 本文提出一种云环境下基于任务分配和数据集副本的科学工作流数据布局方法。该方法对各个任务之间的依赖度进行定量计算,根据依赖度较为均匀地将任务分配至各数据中心。考虑到科学工作流中同一个数据集可能需要多次传输,给出基于数据集副本的两阶段科学工作流数据布局方法,将数据布局细分成初始阶段和运行阶段。实例分析结果验证了该方法的有效性。下一步将结合云环境下优化的科学工作流执行时间进行更深入的数据布局研究。3 数据布局
3.1 数据传输与副本存储费用计算
3.2 初始阶段数据集布局方法
3.3 运行阶段数据布局方法
4 实例分析
4.1 输入设置




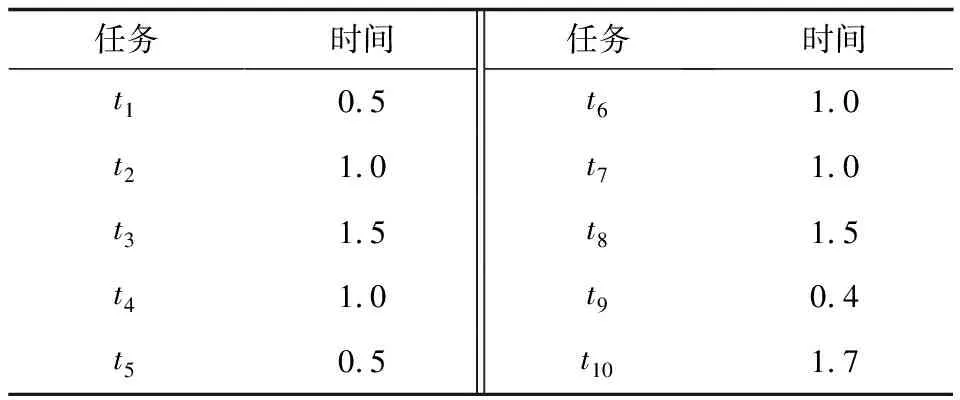
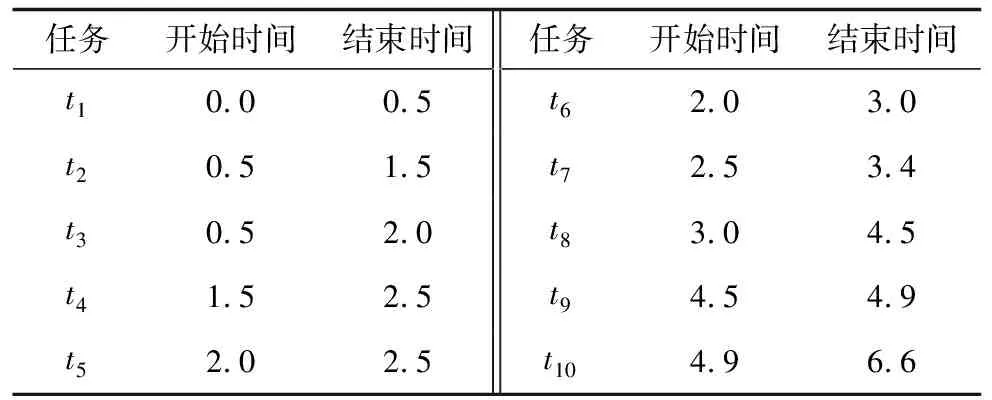
4.2 任务布局
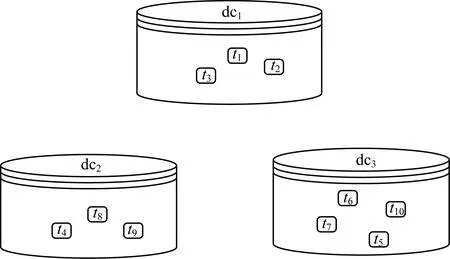
4.3 初始阶段数据集分配
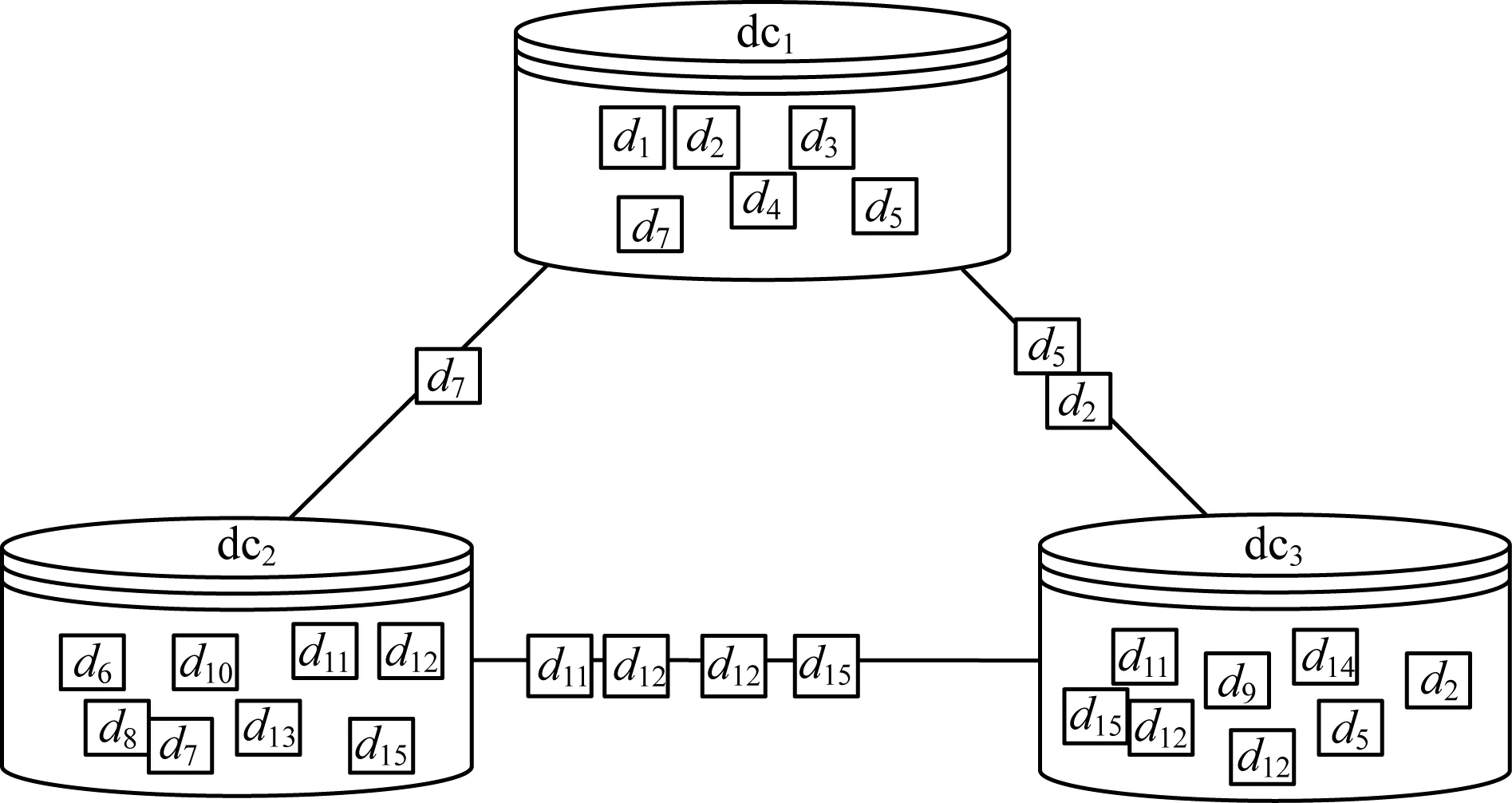
4.4 运行阶段数据集分配
4.5 费用计算



5 结束语

