Lorenz系统与Rossler系统在限定时间内的滑模同步控制
蒋楠, 魏毅强
1.山西广播电视大学公共基础学院, 山西 太原 030027;2.太原理工大学数学学院, 山西 太原 030001
0 引言
混沌系统具有内随机性、分维性、普适性及标度性等特征,并且对初始条件、参数变化具有较强的敏感性和随机性,使得混沌系统的同步控制在保密通信、生物工程、信息信号处理及其他领域得到了广泛应用,同时实现混沌同步的诸多有效方法也相继提出,比如:非线性反馈控制法[1,2]、自适应控制法[3,4]、滑模变结构控制法[5]、模糊同步控制法[6]等.近几年,混沌系统的滑模同步已经成为非线性领域研究的热门课题.由于滑模控制对外界扰动具有较强的鲁棒性和较好的动态性能,受到了学者们广泛的关注.文献[7]通过设计切换函数和控制率,实现了多个分数阶混沌系统的滑模同步;文献[8]研究了一类分数阶参数不确定混沌系统的滑模同步;文献[9]通过结合分数阶运算和整数阶同步控制方法,设计了一种同步控制器,实现分数阶混沌系统的同步.在实际应用中,系统无法避免地受到外界干扰、非线性输入、参数未知等多种因素的影响,针对系统的这些影响因素,学者们提出了多种解决方法.文献[10]针对带有外部扰动项和不确定性的分数阶混沌系统,运用自适应模糊滑模控制方法实现了系统的投影同步;文献[11]在未知参数和外部扰动的情况下,选取分数阶积分滑模面,实现了混沌系统的局部渐近稳定;文献[12]通过设计分数阶积分滑模面,在外界干扰和系统不确定的情况下,实现了两个分数阶混沌系统的同步.上述文献大部分只考虑了外界干扰、系统不确定、非线性输入等因素对系统的影响,却忽略了系统达到同步的时间,而在实际应用中,混沌系统在限定时间内达到同步更具有实际价值和现实意义.
本文构造了一个新的滑模面,通过比较系统同步误差沿着两个滑模面收敛到原点的时间,证明新的滑模面比传统滑模面的收敛速度更快,以含有外界干扰项的混沌系统为研究对象,根据Lyapunov稳定性理论和滑模控制方法,在滑模控制律的作用下,使得同步误差收敛到原点,实现了Lorenz系统与Rossler系统在限定时间内的异结构同步.最后通过数值仿真验证了结论的正确性和有效性.
1 系统模型
选取Lorenz系统为驱动系统
(1)
可将驱动系统改写为如下矩阵形式
(2)
f(x)F(x)θ
因此驱动系统可以表示为
(3)
其中,x(t)为系统的状态变量;f(x)为连续的非线性函数;矩阵F(x)中的元素为连续的非线性函数;θ为参数向量;dm为外部扰动.
选取Rossler系统为响应系统
(4)
可将响应系统改写为如下矩阵形式
(5)
g(x)G(x)φ
因此驱动系统可以表示为
(6)
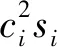
(7)
即
(8)

(9)

则系统(9)在有限时间内稳定,且T满足
引理2[14]对于状态变量x,若初始条件x0>0,满足下列条件
则状态变量x在有限时间内稳定,且时间T满足
2 滑模控制律设计与稳定性分析
2.1 滑模控制律设计
文献[13,15]中的传统滑模面为
(10)
此滑模运动存在的充要条件为
(11)
由此得到误差系统为
(12)
设计新的滑模面为
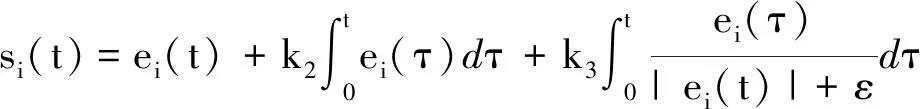
(13)
滑模运动存在的充要条件为
(14)
由此得到误差系统为
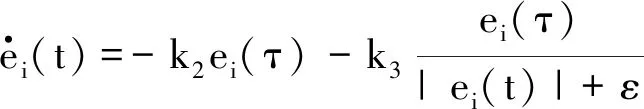
(15)
定理1 如果误差系统的初值ei(0)
证明 分别根据引理1和引理2,收敛时间为
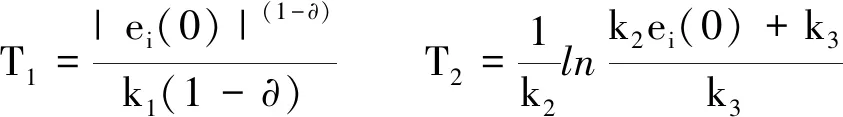

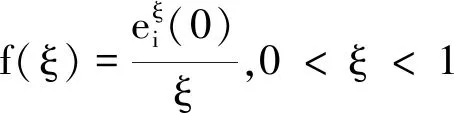
当ei(0) 当k1=k3时,T0 根据自适应控制理论和滑模控制理论,结合所设计的新的滑模面(13),将滑模控制律设为 (16) (17) 定理2 针对混沌同步误差系统(8),选取滑模面(13),在滑模控制律(16)作用下,系统在限定时间 (18) 内收敛到滑模面. 证明 根据Lyapunov稳定性理论,选择Lyapunov函数为 (19) 对(19)式求导得到 (20) 将(14)式代入 (21) 将(8)式与(17)式代入 (22) 代入得 放缩可得 将(16)式代入 为了验证本文所提理论结果的可行性和有效性,以Lorenz系统(1)为驱动系统,Rossler系统(4)为响应系统进行Matlab数值仿真.利用设计的滑模控制律,在系统含有外界干扰项的情况下,实现在限定时间内两个异结构混沌系统的滑模同步.同步误差系统(8)可以表示为如下形式: 图1 切换滑模面 图2 同步误差沿滑模面(13)随时间的变化Fig.2 Time history of synchronized error along the sliding surface(13)图3 同步误差沿滑模面(10)随时间的变化Fig.3 Time history of synchronized error along the sliding surface(10) 基于Lyapunov稳定性理论和滑模控制方法,构造了新的滑模面,设计了滑模控制律,实现了含有外界干扰项的Lorenz混沌系统与Rossler混沌系统在限定时间内的滑模同步,并用数学推理证明了新的滑模面比传统滑模面具有更快的的收敛速度.最后,系统仿真结果表明,本文所提出的理论结果具有正确性和有效性.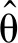
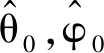
2.2 稳定性分析
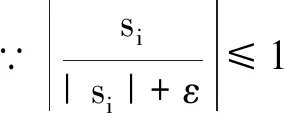
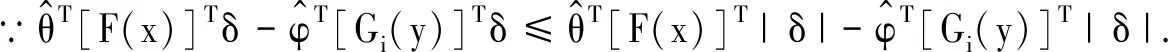
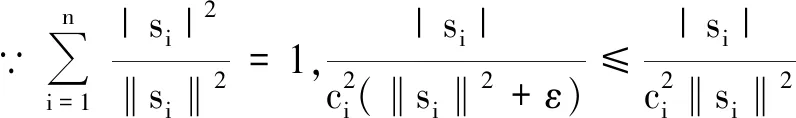
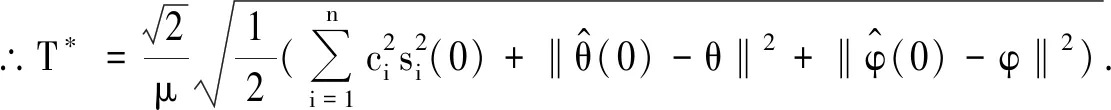
3 数值仿真
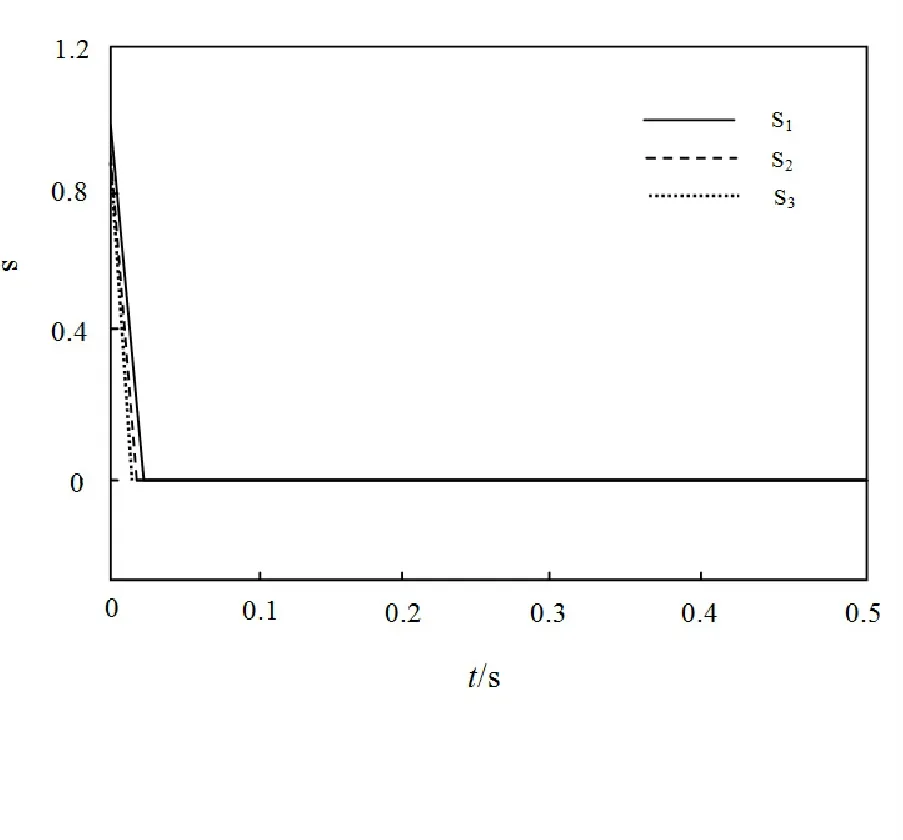
Fig.1 Switch the sliding surface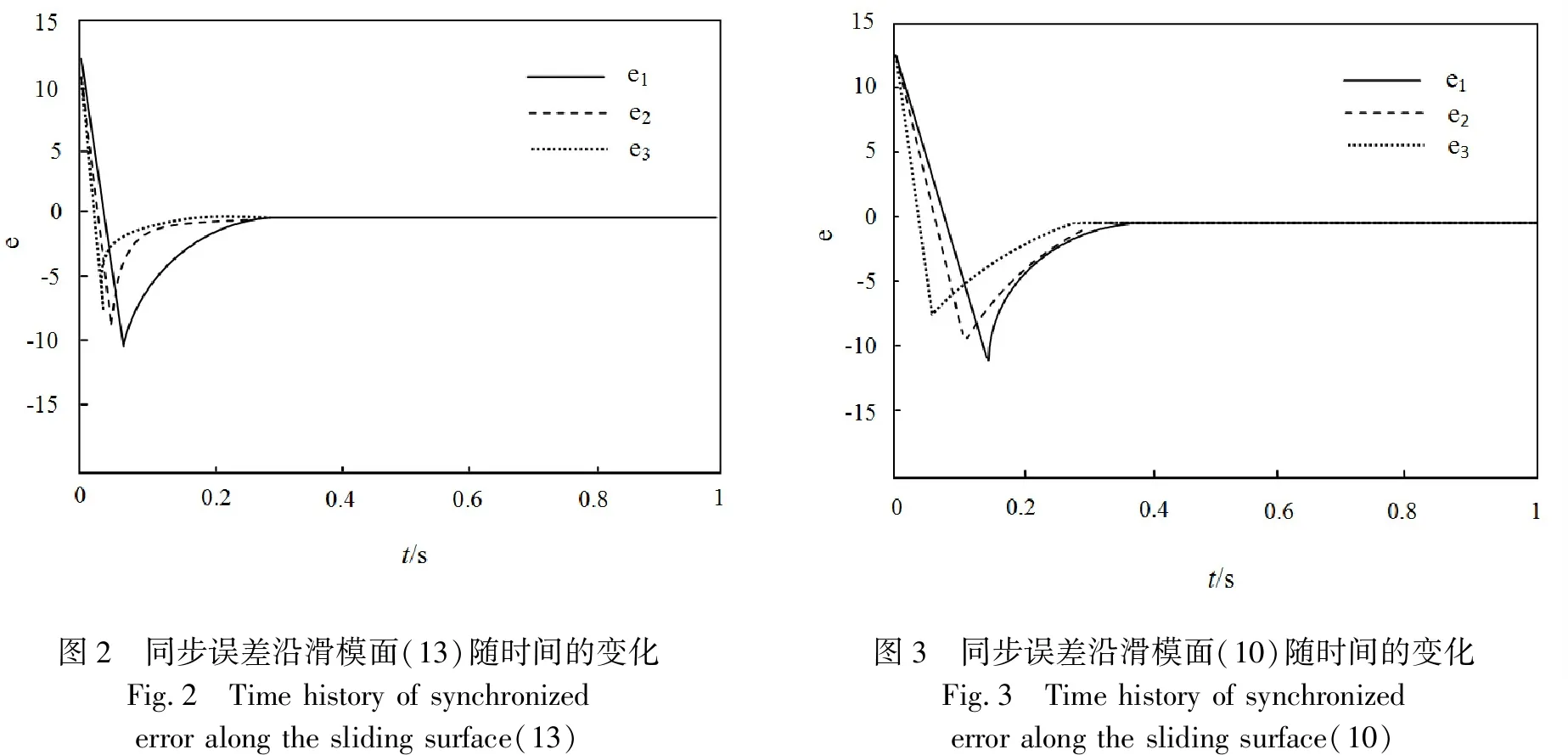
4 结论

