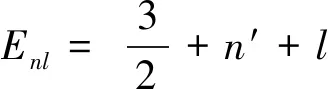球坐标系下三维谐振子的本征问题研究①

张 硕， 李金鑫， 杨继勇， 薛泽利， 张海丰

(佳木斯大学 理学院，黑龙江 佳木斯 154007)

0 引 言

在非相对论量子力学中，谐振子模型是能够严格求解的基本物理模型，其在原子核表面振动、分子振动、辐射场振动、晶格振动等方面都有广泛的应用，因而得到了大量的研究，例如：王亚辉研究了非对易空间中阻尼谐振子的Wigner函数[1-2]；吴淑蕊分析了量子谐振子在非对易空间中的性质[3]；居康康研究了量子耗散谐振子的跃迁几率[4]；郁华玲使用阶梯算符分析了谐振子能量及相干态[5]；李凤敏对磁场中三维各向异性谐振子哈密顿量进行了对角化处理[6]；李兴华研究了球坐标系下三维各向同性谐振子的类经典态[7]；林蓉利用二次型理论对双模耦合谐振子的能级进行了精确求解[8]。本文将给出求坐标系中角动量平方算符和三维谐振子哈密顿算符的本征值和本征波函数，为量子问题的代数解法提供理论支持。

1 球坐标系下角动量平方算符的本征值和本征波函数

(1)

(2)

令Y(θ,φ)=Φ(φ)Θ(θ)，则根据分离变量法，可以得到.

(3)

(4)

(5)

(6)

所以式(5)得到

Φ(φ)=eimφ

(7)

按照周期函数的性质，Φ(φ)满足周期性条件Φ(φ+2π)=Φ(φ)，即e2πim=1，所以m=0，±1，±2，…。

令式(6)中x=cosθ，则

(8)

所以式(6)变为

(9)

进一步变形可以得到勒让德方程

(10)

当对上式做空间反演时，即注意，x→-x，式(10)不变，即表明上式具有对称性。当m2=0时，式(10)变为

(11)

[(s+n)(s+n+1)-λ](anxs+n)}=0

(12)

对于式(12)系数必须为零，所以

(s+n+2)(s+n+1)an+2=

[(1+n)(s+n+1)-λ]an

(13)

即

(14)

(15)

所以，式(10)的通解为

(16)

2 球坐标系下三维各向同性谐振子的本征值和本征波函数

取直角坐标系下三维各向同性谐振子的哈密顿算符为

(17)

首先将动量算符改写为如下形式

(18)

在球坐标系下上式表示为

(19)

利用式(1)可得

(20)

所以，在球坐标系中，哈密顿算符表示为

(21)

(22)

亦或

(23)

所以径向方程可以表示为

(24)

令μ(r)=rR(r)，则上式变为

(25)

(26a)

当r取较大值时，式(26a)变为

(26b)

所以对于r取较大值的情况，令

u(r)～g(r)e-β2/2

(27)

所以

(g″-βg-βrg′+β2r2g)e-βr2/2

(28)

于是可得g(r)的微分方程

(29)

取级数展开式

(30a)

因为a0≠0，所以

(30b)

(30c)

由于

(31)

于是式(29)变为

(32)

当n=-2时

[s(s-1)-l(l+1)]a0=0

(33)

因为a0≠0，所以

s=l+1

(34)

当n=-1时

[s(s+1)-l(l+1)]a1=0

(35)

因为s=l+1，得到a1=0，所以式(32)中

(36)

根据本征波函数的自然条件可知，本征波函数应该是有界的，所以截取g(r)为n0项有限次幂多项式，令an0=0，所以

(37)

即

(38)

所以可得能量本征值为

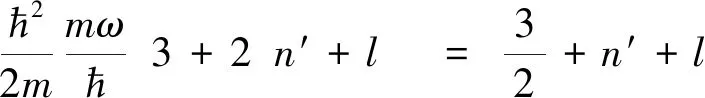
(39)

可见，所得的本征值和直角坐标系下得到的结果是一致的。

3 结 论