跨座式单轨固定铸钢支座接触应力研究

张晓飞 蒲黔辉 王瑞吉

（1.西南交通大学 四川成都 610031；2.四川交大工程检测咨询有限公司 四川成都 610031）

1 引言

跨座式单轨交通系统是为适应城市快速交通而出现的一种新型交通形式，最早出现于19世纪80年代的法国，上世纪60年代德国、美国等许多西方国家也相继修建了多条跨座式单轨交通线路[1]，由于其具有安全舒适、经济适用、保护环境等诸多优点，在世界范围内得到越来越广泛的应用。我国第一条跨座式单轨交通线路是重庆市轨道交通2号线，克服了重庆市地形复杂、道路狭窄、建筑物密集等交通建设难点，改善了居民出行与环境质量，同时也为我国其他山地城市的轨道交通建设提供了示范性工程，为跨座式单轨交通系统的进一步推广和应用创造了有利条件[2]。

铸钢支座是跨座式单轨交通系统中的重要设施，它连接着轨道梁与墩台，能够承受轻轨列车高速运行产生的垂直纵横向荷载、扭转荷载以及冲击荷载等多种荷载组合，并将荷载传递至桥墩。为满足轻轨列车行驶时安全可靠、平稳及低噪声的要求，铸钢支座需要较高的强度和优异的抗磨损、抗疲劳及防腐蚀性能，因此，铸钢支座的选材、制作加工等要求比一般桥梁支座的要求高很多[3]。

现阶段对于跨座式单轨的研究主要集中在车桥动力学和疲劳强度方面。国内一些学者结合重庆市单轨列车运行反馈的信息，对跨座式单轨展开了一系列车桥振动研究与轨道梁静动力分析，并取得了一定的成果[4-10]。少数学者通过对铸钢支座进行疲劳试验来检验支座的疲劳强度，试验结果表明铸钢支座能够满足疲劳强度要求[11-12]。

然而，随着跨座式单轨技术的逐步发展，对铸钢支座的强度和耐久性也提出了更高的要求。由于铸钢支座各部件连接处接触面积较小，导致接触应力较大，支座长期服役后易产生磨损，降低了支座的耐久性。目前关于铸钢支座接触应力的研究很少。所以对支座接触应力进行研究，分析影响接触应力的因素及其影响机制，可以指导铸钢支座的优化与设计，降低接触应力水平，有利于减小铸钢支座的磨损，提高支座耐久性，减小轻轨交通系统的维护成本。

本文基于Hertz接触理论，对跨座式单轨PC梁固定铸钢支座的接触应力进行分析，并建立三维有限元模型研究支座的受力状态，通过试验验证有限元分析的可靠性。

2 接触分析

（1）支座结构

跨座式单轨PC梁固定铸钢支座由上摆、铰轴和下摆组成，铰轴贯穿上摆和下摆的摆孔，通过止脱板限制铰轴的侧向脱出，从而形成一个整体，固定支座的结构如图1所示。其中上摆通过预留钢筋与轨道梁现浇成一体，下摆通过4个地脚螺栓锚固于墩台上。固定支座相当于固定铰支座，能够通过铰轴实现自由转动但是不能水平移动。

（2）几何简化与弹性模拟

图1 固定铸钢支座结构示意

固定支座铰轴与上下摆摆孔间的接触是如图2a所示的同形接触，接触面积较小导致了应力集中现象，进而接触面间较大的应力水平会影响支座的静力强度和耐久性。根据Hertz线接触理论，将上述同形接触问题进行几何简化，转化成一当量弹性圆柱和一刚性平面的接触问题[13-14]，如图2b所示，其中当量弹性圆柱的半径R满足:

式中，R1为铰轴半径；R2为摆孔半径。

当量弹性圆柱的弹性模量E*满足:

式中，E1为铰轴的弹性模量；E2为上下摆的弹性模量；ν1为铰轴的泊松比；ν2为上下摆的泊松比。

图2 铰轴与摆孔接触类型

（3）接触应力

当量弹性圆柱在荷载作用下，接触区由一条线扩展成一个狭长的面，如图3所示，接触区半宽度b为:

式中，F为荷载；L为当量弹性圆柱长度。

在接触区内，接触应力p满足半椭圆分布，即:

式中，pH为最大Hertz应力，即x＝0时接触区域的中心处所受到的接触应力，pH＝2 F/πbL。

（4）影响因素

图3 荷载作用 后接触区扩展

根据Hertz理论，接触应力的大小与接触体的材质和尺寸、作用力的大小、接触区宽度以及距离接触中心的远近等因素有关。在支座的接触问题中，支座各部件的材质、作用在支座上的荷载、铰轴直径与长度、支臂摆孔孔径等都将影响支座的接触应力水平。

3 有限元分析

3.1 建立有限元模型

利用ABAQUS有限元计算软件，首先建立固定钢支座的实体模型，再进行网格划分得到图4所示的三维有限元模型。单元类型为非协调模式的八结点线性六面体单元（C3D8I），模型的接触属性定义为法向采用硬接触，切向采用罚函数摩擦，摩擦系数为0.11。铸钢支座各部件材料及物理性能见表1。其中，上下摆材质为铸钢，铰轴材质为合金钢。

图4 固定支座的三维实体和有限元模型

表1 固定钢支座各部件的材料参数

3.2 计算荷载

按照支座设计单位提供的最不利荷载考虑，支座承受的最大竖向荷载为1 239 kN，不考虑摇摆力与风力等横向荷载，不计支座自重。

3.3 边界条件

实际情况下，铸钢支座下摆通过4个地脚螺栓锚固在墩台上。竖向荷载产生的压应力作用在上摆上，通过铰轴传递给下摆，又通过螺栓传递给墩台，这种情况下可将下摆底部视为固定约束。

（1）位移边界条件

在支座模型下摆4个螺栓孔处施加三个方向的位移约束和转角约束。支座各部件通过摩擦接触连接，无边界约束。

（2）荷载边界条件

竖向荷载等效为分布面力，作用在支座上摆顶面。

3.4 有限元计算结果分析

（1）应力分析

通过ABAQUS静力分析得到固定支座的应力云图，作Y方向切片处理，可以得到支座的整体应力分布情况，如图5a所示。单独显示支座各部件的应力云图，得到各部件的应力分布情况，如图5b～图5d所示。

由图5a可知，固定支座上下摆与铰轴相接触位置的边缘存在最大应力255.4 MPa，低于屈服强度340 MPa。应力在摆孔切向平面内呈伞状分布，在摆孔法向平面内呈肺叶状分布。

上摆的应力分布图如图5b所示，上摆的最大接触应力为226.1 MPa，低于屈服强度340 MPa，作用在摆孔上方，应力呈倒等边梯形分布。由图5c可知下摆最大接触应力为255.4 MPa，低于屈服强度340 MPa，作用在摆孔下方，应力呈伞状分布，支臂与底板连接处存在应力集中。如图5d所示，铰轴的最大接触应力为100.9 MPa，低于屈服强度785 MPa，中下部的应力较大，往上逐渐减小。

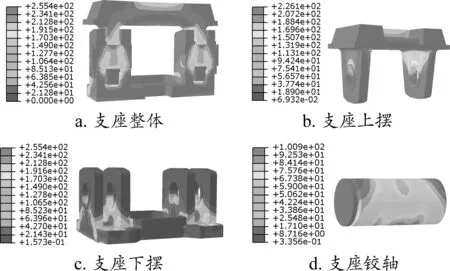
图5 支座整体及主要部件的应力云图(单位:MPa)

有限元计算结果显示，固定支座上下摆应力水平较接近，铰轴应力低于上下摆应力。

（2）位移分析

设计荷载作用下，支座的竖向位移变形如图6所示，变形主要发生在上摆的顶板、支臂和下摆的支臂处，最大位移为0.435 mm，出现在上摆顶板中部，位移变形较小，说明支座在设计荷载作用下具有足够的刚度。

图6 固定支座位移变形图(单位:mm)

4 试验分析

4.1 静力试验分析

为了检验铸钢支座的强度是否满足要求，并验证理论分析结果的可靠性，对固定钢支座进行了竖向力荷载试验，竖向荷载为1 239 kN，荷载作用在固定支座顶面中心。静力荷载试验加载装置为MTS电液伺服结构试验系统，加载方式为逐级加载直至达到1 239 kN后持荷加载5 min。固定支座底部锚固在现场浇筑的混凝土块上，混凝土块通过螺杆锚固在试验场地上。为了防止加载过程中支座发生侧倾，在试验支座旁设一辅助支座，两者通过钢板连接，辅助支座不直接参与加载。

4.2 测点布置

（1）应变测点

固定支座上摆、下摆根部的应变测点均为应变花，铰轴的应变测点为单片，具体测点布置位置如图7所示。

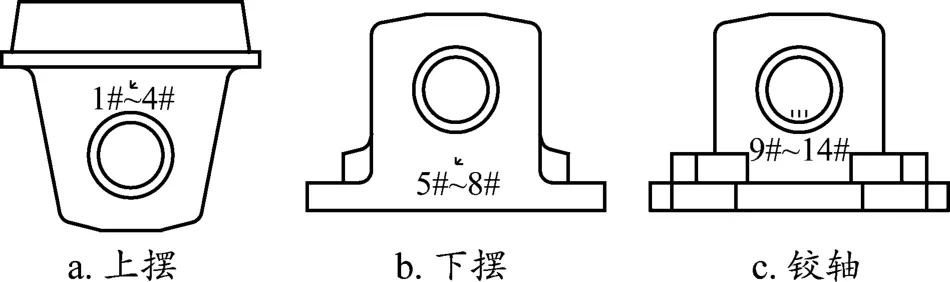
图7 应变测点布置

（2）位移测点

位移变化主要考虑了支座在设计荷载作用下的竖向变形，考虑到支座的变形较小，故采用千分表进行测量，位移变形测点布置于上摆底面中心。

4.3 试验结果

静力荷载试验结果列于表2，其中，正值表示拉应力，负值表示压应力。

表2 固定支座静力荷载试验结果

试验结果表明，支座上下摆根部与铰轴端部在设计荷载作用下多为压应力。上下摆最大应力均发生在内侧支臂根部，铰轴中下部应力最大，并且上摆应力水平高于下摆应力水平，铰轴应力介于两者之间。各部件的最大应力均低于屈服强度。

在设计荷载作用下固定支座发生最大变形值为0.280 mm。挠度测试结果表明在设计静力荷载作用下，支座处于弹性工作状态。

5 有限元结果与试验结果的比较

5.1 应力分析结果对比

对照静力荷载试验应变测点位置，在有限元计算后处理模块中提取出模型对应位置的应力结果，并将有限元计算得到的应力结果与试验得到的应力结果绘于柱形图中，如图8所示。由图可知，除个别测点应力结果不一致外，接近80%的测点应力相差不大，说明有限元计算结果与试验结果吻合较好，有限元计算结果具有参考价值。

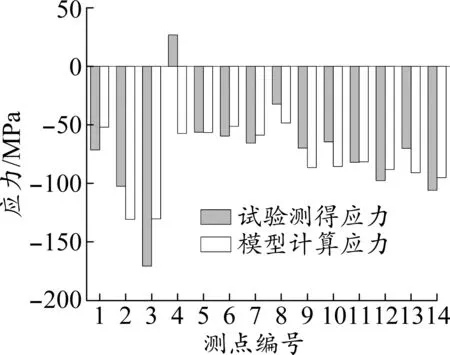
图8 应力对比

5.2 位移结果对比

试验得到支座的最大位移为0.280 mm，而有限元计算得到支座的最大位移为0.453 mm，是前者的1.6倍。分析认为两者结果差异较大可能是由于荷载加载方式的差异、边界条件的处理不合理或测量误差等原因造成的。

6 影响因素及其影响机制分析

在支座接触问题中，分析影响接触应力的各个因素，其中，支座各部件的材质一般为铸钢或合金钢，由材质决定的弹性模量波动不大，因此材质对接触应力的影响不大；作用力的大小是由外荷载决定的，作用在支座上的外荷载越大，接触应力就越大，这一影响因素是由外部条件控制的。所以，由支座本身结构决定的、对接触应力影响显著的因素是接触区面积，即铰轴直径的大小。

为了反映铰轴直径对接触应力的影响，通过有限元软件ABAQUS计算分析了相同荷载情况下铰轴直径尺寸变化时支座的接触应力，并以铰轴直径与摆支臂宽度的比值（D/B）为横坐标，以接触应力的大小为纵坐标，绘制曲线图。

由图9可知，当铰轴直径过小时，接触应力会超过材料的屈服强度，随着铰轴直径的增大，接触应力逐渐减小至屈服强度以下。当铰轴直径增大至一定水平时，接触应力不再减小而是趋于平缓。考虑到铰轴直径过大时，不会进一步减小接触应力，并会使铰轴过于笨重，造成资源浪费，因此铰轴直径的经济合理尺寸范围是摆支臂宽度的0.38～0.41倍。

图9 铰轴直径占臂宽的比值与接触应力关系

7 结论

（1）在设计荷载作用下，跨座式单轨PC梁固定铸钢支座各部件最大接触应力均未达到材料的屈服强度，满足使用要求。

（2）设计荷载作用下，固定支座上下摆最大接触应力达到了材料屈服强度的75%左右，既不会浪费材料又有一定的安全储备；而铰轴的最大接触应力只达到了材料屈服强度的11%，较大的强度富余造成材料的浪费，可以适当降低铰轴材料等级。

（3）有限元计算的应力结果与试验结果吻合较好，说明有限元计算结果是可靠的。由于试验中接触面间的应力无法进行测量，只能通过有限元手段分析计算，这也说明理论分析具有独到的长处。

（4）铰轴直径的尺寸会影响接触应力的大小。当铰轴直径尺寸小于摆支臂宽度的26%时，铰轴与摆孔间的最大接触应力会超过材料的屈服强度；当铰轴直径占支臂宽度的26%～38%时，最大接触应力逐渐降低，并始终低于屈服强度；当铰轴直径超过支臂宽度的38%时，最大接触应力趋于平缓。故铰轴直径占摆支臂宽度的38%～41%时是经济合理的，在进行支座的设计时，可以参考以上范围。