任意截面钢筋混凝土构件配筋计算方法

朱勇战

（中铁第五勘察设计院集团有限公司 北京102600）

1 引言

钢筋混凝土构件在工程结构中广泛应用，例如:单层厂房排架柱，多层框架结构，刚架中的横梁和墩柱，隧道拱圈，钢筋混凝土拱桥的拱肋，桥墩基础以及桩基础等。经常会遇到钢筋混凝土构件双向大偏心受力的问题，当作用在构件上的纵向力相对于截面的两个主轴均有偏心，或者是构件同时承受轴心压力和两个方向的弯矩时，构件的受压区形状因纵向力及偏心距的大小不同而不同，呈三角形、四边形或是五边形。并且弯矩作用平面与弯曲平面不重合，亦不与截面边缘相平行，中和轴的位置随截面尺寸、砼强度、配筋、荷载形式及大小等诸多因素的变化而变化，使得中和轴位置的确定相当复杂，需要进行多次试算，计算繁琐，一般的钢筋混凝土结构设计原理书籍都没有进行论述。国内学者在此方面做的研究较少，其中余琪[1]、童森林[2-3]通过图形分割，运用平移轴、旋转轴、坐标变换，迭代求解最终零应力线方法分别研究了矩形截面和圆端截面配筋计算问题，求解出了混凝土最大压应力和钢筋最大拉应力。针对双向偏心受压计算[4-6]，学者们分别采用不同的简化计算方法，也取得了一定的成果，本文基于容许应力法公式推导，解决了钢筋混凝土构件任意截面配筋计算问题。

2 钢筋混凝土构件偏心受压常用计算方法

2.1 混凝土规范中的设计公式

我国现行的规范《混凝土结构设计规范》（GB 50010-2010）附录E中给出了任意截面构件正截面承载力计算公式[7]:

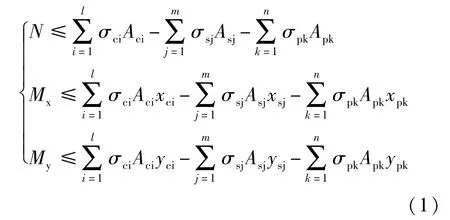
式中具体的参数说明参考《混凝土结构设计规范》（GB 50010-2010）附录E，采用将受压区混凝土划分成微小单元的思路，理论上讲该计算公式可适应于任意截面钢筋混凝土构件，但是对于任意不规则截面而言，手动迭代计算基本不可能，编程求解，每迭代求解一次需要重新对截面进行网格划分，截面的边界范围判断极为困难，并且网格划分的大小对求解精度影响较大，求解效率极低。

2.2 公路钢筋混凝土及预应力混凝土桥涵设计规范设计公式

我国现行的规范《公路钢筋混凝土及预应力混凝土设计规范》（JTG 3362-2018）第5.3.11条中给出了钢筋混凝土双向偏心受压构件其正截面抗压承载力计算公式[8]:

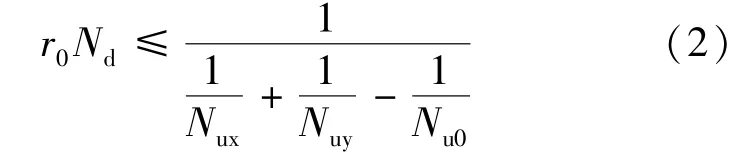
式中具体的参数说明参考相应规范条文，该公式仅适用于截面具有两个相互垂直对称轴的钢筋混凝土构件，计算公式简单，可直接用于截面设计，但仅适用于双向均为小偏心受压的情况，对大偏心且侧边钢筋较多时计算误差偏大。

2.3 铁路桥涵混凝土规范设计公式

我国现行的规范《铁路桥涵混凝土结构设计规范》（TB 10092-2017）第6.2.5条按照容许应力法仅给出了混凝土压应力的计算公式[9]，公式仅适用于单向偏心受力构件，基本没有可实施性。黄棠主编的《结构设计原理》[10]依据容许应力法，推导出了矩形截面、箱形截面、工字形截面、圆形截面、圆环截面单向受压状态下的钢筋应力和混凝土应力计算公式，也是目前铁路钢筋混凝土构件设计中应用较多的计算方法，针对铁路桥梁也有应用极限状态设计方法进行的相关研究[11]。

目前的计算公式和方法主要针对均匀配筋的规则截面，而对非均匀配筋的不规则截面都没有好的解决方法。针对这个问题，本文借助《混凝土结构设计规范》的计算思路，通过进一步的公式推导，解决了钢筋混凝土任意截面配筋的计算问题，并编制了容许应力法任意截面配筋程序，可适用于钢筋混凝土构件单（双）向受弯、偏心受压、偏心受拉的应力计算。

3 任意截面配筋验算公式推导

钢筋混凝土构件配筋验算采用的容许应力法，容许应力法为弹性设计理论，不考虑混凝土材料塑性以及受拉混凝土参与受力，且截面受力仍符合平截面假定。借助微积分的思路，可将受压区混凝土划分为多个极小混凝土单元，并近似取每个单元内应变应力均匀分布，如图1所示，截面轮廓为A1～An，截面外轮廓存在曲线时按以直代曲考虑，将曲线划分成多直线段，BC为截面中性轴，其中A1BCAn-1An为受拉区混凝土，另一侧即为受压区混凝土。

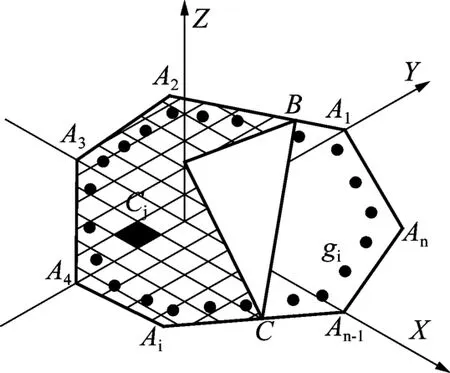
图1 截面单元划分示意

根据截面的受力和应力分布可列出力平衡方程。

式中，N为截面轴力（kN）；Mx、My为绕X轴和Y轴的弯矩（kN·m）；ηx、ηy为验算截面上弯矩偏心放大系数，计算方法可参见《铁路桥涵混凝土结构设计规范》；σgi、σcj为第i个钢筋单元、第j个混凝土单元的应力（MPa）；Agi、Acj为第i个钢筋单元、第j个混凝土单元的面积（m2）；xgi、ygi为第i个钢筋单元坐标（m）；xcj、ycj为第j个混凝土单元的重心坐标（m）。

任意截面由于双向受弯影响，截面的中性轴位置确定相当复杂。根据平截面假定，截面中性轴即为构件弯曲平面与截面的交线。空间坐标系内混凝土截面应力平面方程为:

则受压截面任意点的混凝土应力为:

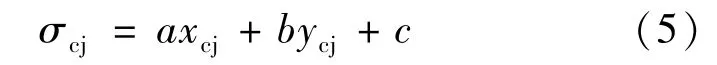
相同位置钢筋与混凝土应变相同，若钢筋与混凝土的弹模比值为n，则任意点的钢筋应力为:

代入到平衡方程可得到:

将方程（7）展开后可写成:

结合上述表达式所对应的物理意义，方程（8）可转化为:

式中，Ac为受压混凝土截面面积（m2）；Scx、Scy为受压混凝土截面面积矩（m3）；Icxx、Icyy为受压混凝土截面惯性矩（m4）；Icxy为受压混凝土截面惯性积（m4）；Ag为截面钢筋面积（m2）；Sgx、Sgy为截面钢筋面积矩（m3）；Igxx、Igyy为截面钢筋惯性矩（m4）；Igxy为截面钢筋惯性积（m4）；

从公式的推导过程来看，求得了受压截面和所有钢筋单元的几何特性，解三元一次方程组即能得到空间应力平面方程系数a、b、c。由于受压截面本身是一个与空间应力平面方程系数a、b、c关联的变量，因此方程系数a、b、c的求解过程是一个不断迭代的过程，而任意截面应力的求解问题转化成了简单的任意截面几何特性的求解问题。

4 任意截面几何特性求解

根据积分变换格林公式[12]求解任意截面几何特性，设封闭区域D由分段光滑的曲线L围成，函数P（x，y）及Q（x，y）在D上具有一阶连续偏导数，则有:

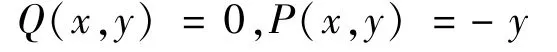
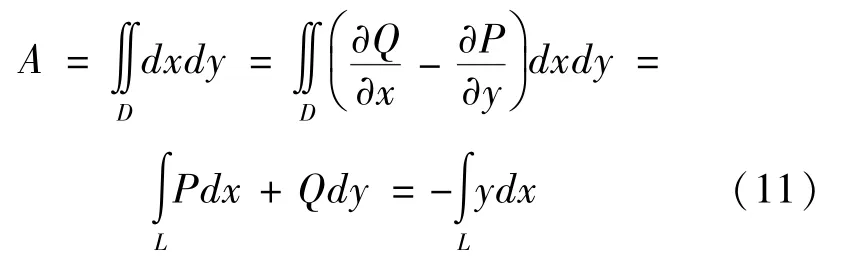
曲线积分对路径具有可加性，图1中以Ai和Ai+1截面轮廓点组成的直线段表达式为:

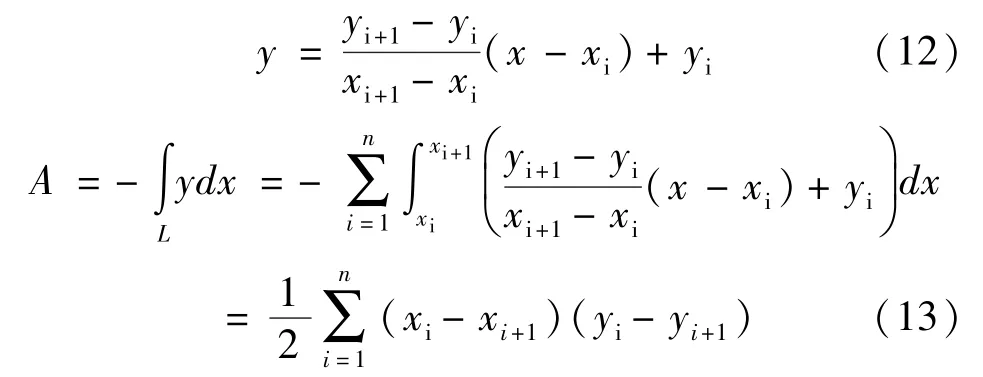
同理可计算任意多边形其他几何特性:

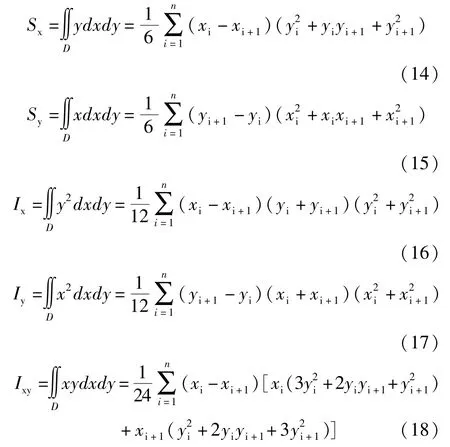
公式（10～18）不仅适用于单连域，同时也适用于多连域，需要将多连域之间用边线相互连接成封闭区域，封闭曲线对于外层区域按逆时针连接，内侧区域按顺时针连接。

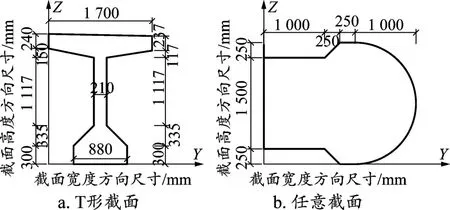
图2 不规则截面尺寸示意

通过选取图2所示两种截面形式，对公式（13～18）计算结果进行验证，计算结果见表1。

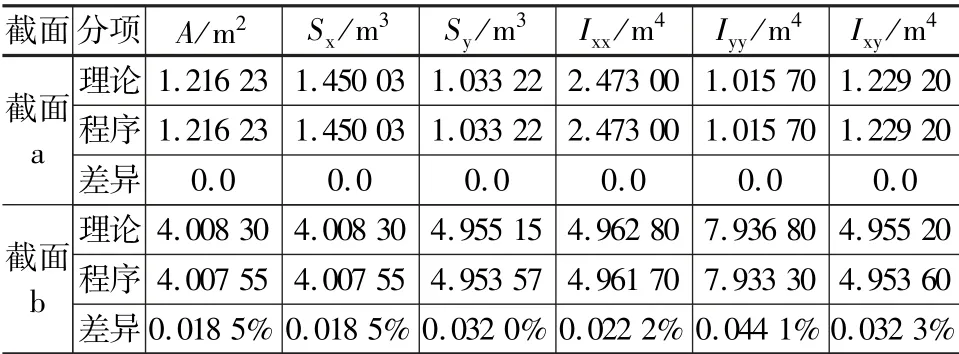
表1 截面特性计算结果验证

通过选取两种不规则截面并采用本文的计算公式计算，轮廓线由折线组成的截面理论与程序计算结果一致，带有曲线截面程序计算时将曲线离散成长度不超过0.05倍曲线半径的直线，程序计算截面特性与理论计算的结果差异不超过0.05%，说明合理地控制曲线分段长度，采用本文提出的计算方法得到的不规则截面几何特性结果正确，满足设计要求。

5 任意截面配筋验算程序实现

任意截面由于截面轮廓和截面配筋的复杂性，且应力平面求解需要不断迭代，因此整个计算过程采用手动计算工作量较大，根据前面的理论推导，采用数值分析方法进行程序设计，整个计算过程主要分为以下几个步骤:

（1）根据输入参数生成任意截面外轮廓点坐标（xci，yci），钢筋坐标（xgi，ygi），也可以直接输相应点的坐标。首先根据截面轮廓点坐标运用公式（13～18）计算截面出对应的6个截面特性参数，得到截面的形心坐标Xc＝Sy/A，Yc＝Sx/A，通过坐标平移变换将所有坐标点平移至以形心坐标为原点的参考坐标系中，重新计算毛截面的几何特性参数。

（2）根据计算得到的截面几何特性，输入截面验算外力N、Mx、My，钢筋混凝土弹模比，单根钢筋面积以及偏心受压构件验算长度Lx、Ly计算相应偏心受压弯矩放大系数。

（3）然后根据计算公式（9）解三元一次方程组，计算初始应力平面方程系数a0、b0、c0，求解应力平面与截面的交线，通过公式σcj＝a0xcj+b0ycj+c0计算混凝土截面轮廓点应力，判断有效混凝土受压轮廓节点，与所求得应力平面和截面交线形成有效受压混凝土截面。

（4）调用任意截面几何特性求解程序重新计算有效受压混凝土截面特性和钢筋单元截面特性，代入方程组（9），重新求解方程组可得到新的应力平面方程系数a、b、c。

（5）不断重复（3）、（4）迭代计算求解，如果｜a0-a｜+｜b0-b｜+｜c0-c｜＜ε则计算收敛，计算中取ε＝10-7。否则令a0＝a，b0＝b，c0＝c，进行迭代计算。

（6）最后分别计算混凝土截面和钢筋的应力分别为:σci＝axci+byci+c，σgi＝n（axgi+bygi+c）。

6 算例对比及应用

6.1 单向受力特殊截面钢筋混凝土构件受力分析

对比算例选自参考文献[10]，具体的计算参数如表2、表3所示，计算结果如表4所示。

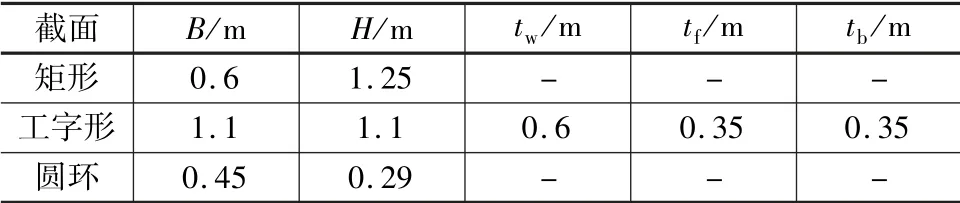
表2 验算截面参数

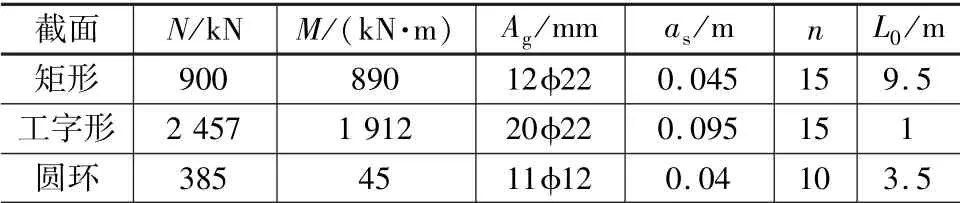
表3 验算截面配筋及受力

表4 计算结果对比

从表4可以看出，根据本文计算方法编制程序的计算结果与文献[10]计算结果吻合，最大差异在1%以内。

6.2 圆端形空心截面钢筋混凝土构件双向受力分析

对比算例选自文献[3]，圆端形直线段长度为2.1 m，外圆弧半径1.15 m，内圆弧半径1.0 m，钢筋所在圆弧半径1.1 m，钢筋单位长度宽1 mm，弹模比取10，轴力N＝8 000 kN，弯矩Mx＝6 000 kN·m，弯矩My＝9 000 kN·m，计算结果如表5所示。从表5可以看出，根据本文计算方法编制程序的计算结果与文献[3]计算结果吻合，最大差异在1%以内。

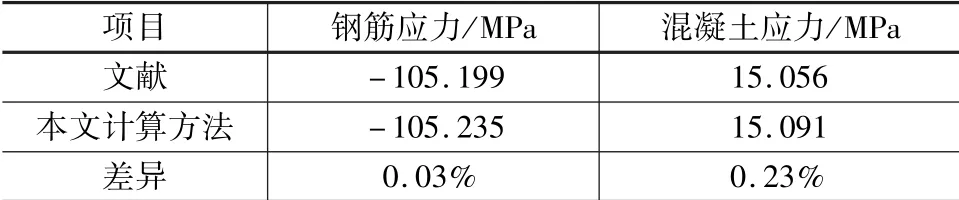
表5 圆端形空心截面计算结果对比

6.3 圆端形实体截面混凝土构件应力重分布计算

对比算例选自文献[3]，圆端形直线段长度为2.1 m，圆弧半径1.15 m，轴力N＝5 301 kN，弯矩Mx＝1 960 kN·m，弯矩My＝3 741 kN·m，计算结果如表6所示。

表6 圆端形实体截面计算结果对比

从表6可以看出，根据本文计算方法编制程序的计算结果与文献[3]计算结果吻合，最大差异在1%以内。

7 小结

（1）本文以材料力学原理中平截面假定为依据，基于容许应力法推导出了任意截面钢筋混凝土构件的配筋验算公式，解决了任意截面受压、受拉、受弯、单（双）向偏心受压和偏心受拉构件配筋验算问题。

（2）钢筋混凝土截面应力计算问题转化为截面几何特性的求解，利用格林积分变换公式简单高效地实现了任意截面的特性求解，计算结果精确可靠。

（3）依托本文计算公式编制的任意截面钢筋混凝土配筋验算程序，提高了计算速度和精度，经过大量算例与对比验算，证明本文方法以及程序计算结果可靠性，目前已经应用于多条铁路特殊结构桥梁工程设计中。