“探究弹簧弹力与形变量的关系”实验中弹簧重力的影响分析

徐可刚

(甘肃省酒泉中学 甘肃 酒泉 735000)

1 “轻弹簧”模型下的数据处理

(1)将弹簧放置在水平桌面上，测量弹簧静止时的自然长度l0.

(2)将弹簧与一刻度尺并排且竖直悬挂，并让刻度尺的零刻线与弹簧上端对齐，在弹簧下端悬挂不同数量的钩码，待弹簧稳定后，分别记录悬挂钩码的重力Gi(i=1，2，3，…)和对应弹簧的长度li(i=1，2，3，…).

根据平衡条件可知，弹簧弹力等于钩码重力，有Fi=Gi．“轻弹簧”自身重力不计，弹簧的形变量为xi=li-l0．

(3)我们以弹簧弹力Fi为纵坐标，以弹簧的形变量xi为横坐标，建立直角坐标系．将各组数据(Fi，xi)的对应点描绘在坐标系中，并用平滑曲线连接，便得到了弹簧弹力Fi与形变量xi的关系图象，即F-x图像．

理想结果应如图1所示，图线是一条过原点的直线．

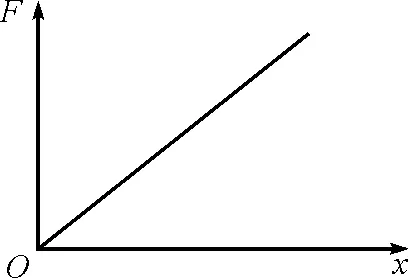
图1 理想的F-x图像

2 “实际弹簧”模型下的数据处理

实际弹簧受一定的重力，将弹簧竖直悬挂后，由于自身重力作用，弹簧会产生一定的形变量．

2.1 弹簧由于自身重力产生的形变量

将一个劲度系数为κ，质量为m的均匀弹簧水平放置．以弹簧一端点为坐标原点O，沿其长度方向建立一维坐标系如图2所示，则弹簧沿长度方向各部位均可用坐标x(0≤x≤L)表示．

从各学科对中高端酒店的研究分布图可以看出，对中高端酒店研究最多的是服务业经济，占比达43.68%；其次是贸易经济，占比为22.99%；排名第三的是宏观经济管理与可持续发展，占比9.20%；旅游科学仅占比仅2.3%，排名第八。详见图2。

图2 弹簧水平放置

取x到x+dx的一小段弹簧，该段弹簧的劲度系数为

(1)

如图3所示，将弹簧竖直悬挂后(未悬挂钩码)，该段弹簧上端的受力为

下端的受力为

(2)

图3 弹簧竖直放置

联立式(1)、(2)可得

(3)

对式(3)积分可得整根弹簧的伸长量为

(4)

2.2 弹簧自身重力产生的形变量对实验数据处理的影响

实验中将弹簧竖直悬挂时，由于自身重力作用，弹簧已经产生了x0的形变量，此时弹簧(未悬挂钩码)的初始长度为

l0′=l0+x0

悬挂钩码后，弹簧的形变量进一步增大．当弹簧长度为li时，弹簧由于悬挂钩码而增加的伸长量为

xi=li-l0′=li-(l0+x0)

此时，对应弹簧弹力的增加量Fi等于悬挂钩码的重力Gi．根据胡克定律，有

Fi=κxi=κ[li-(l0+x0)]=

κ(li-l0)-κx0

(5)

联立式(4)、(5)可知

(6)

若我们仍然把弹簧当做“轻弹簧”处理，则认为弹簧的形变量x等于弹簧悬挂钩码后的长度li与其自然长度l0的差值，即x=li-l0，则有

描点作图后F-x图像将如图4所示，是一条不过原点的直线，与胡克定律不符．

图4 实际F-x拟合图线

2.3 具体实验中该如何解决弹簧自身重力的影响

弹簧由于悬挂钩码增加的伸长量为

根据胡克定律有

(7)

以弹簧弹力的变化量F′为纵坐标，以弹簧形变量的变化量x′为横坐标，描点作图，图像是一条过原点的直线，说明弹簧弹力的变化量与其形变量的变化量成正比．这也间接说明了弹簧弹力与形变量成正比．

3 结论