基于可公度性理论的干旱预测方法研究
李松旌 ,樊向阳 ,景若瑶 ,胡 超 ,王和洲,黄仲冬
(1.中国农业科学院 农田灌溉研究所,河南 新乡453002;2.中国农业科学院 研究生院,北京100081;3.中国农业科学院 农业水资源高效安全利用重点开放实验室,河南 新乡453002;4.中国农业科学院 新乡农业水土环境野外科学观测试验站,河南 新乡453002)
0 引 言
干旱是全球普遍存在且对人类生产、生活造成损失和影响最为严重的一种自然灾害,其具有随机性、持续时间长、影响范围广等特点[1]。干旱不仅造成水资源短缺、生态环境恶化等问题,还可能引发经济失调、饥荒、社会动荡等社会问题[2-4]。因此,提高对干旱发生频率、强度和持续时间的监测和早期预警水平,从而避免干旱带来的负面影响,是干旱研究领域的一项重要内容[5]。
干旱预测主要通过分析各种时间尺度上的干旱变量,如降雨量、径流量、地下水位和土壤湿度等数据的时间序列来实现的[6-7]。国内外针对干旱预测开展了较多的研究,早在1963年,E.J.GUMBEL[7]即利用第三渐进分布式模型进行了干旱预测,但采用的线性回归模型需要收集气压、气温、海洋表面温度、风速、风向以及降水数据等诸多参数[8];Lohani等[10]采用时间序列模型(ARIMA)进行了干旱短期预测;Cordery等[11]基于海表温度和内陆天气、急流、厄尔尼诺现象等相关参数进行了中长期干旱预测。国内学者分别采用灰色系统理论[12-17]、森林随机模型(RF)[18]、神经网络模型(BP)[19-23]、极限学习机(ELM)[24-25]等方法对干旱进行了预测研究,其中灰色理论系统模型在中长期预测时存在较大偏差;RF在划分较多属性的数据上产出的属性权值可信度不高;BP具备较强的非线性拟合能力且预测精度较高,但仍存在诸如局部极小化、结构选择不一、收敛速度慢等不足;作为单隐层前馈神经网络算法的ELM虽然具有较快的学习速度,但存在不稳定和泛化能力不足等缺点。
20世纪80年代,我国学者翁文波基于自然界中普遍存在的周期性,提出了可公度性理论[26],认为可公度是周期性的扩张,并将可公度性理论应用到天灾预测科学中,通过该理论验证了1976年唐山大地震,成功预测了1982年我国华北地区的干旱、1991年长江洪水和1992年美国加州地震[27]等。1982—1992年间国内学者采用该理论先后预测各种自然灾害共252次,准确率高达83.7%[28];国外学者也在材料结构[29]、天文[30]方面验证了基于可公度性理论预测方法的准确性。在干旱预测方面,门可佩[32]利用可公度性理论及可公度系结构示意图预测了我国2000年、2004年、2010年和2016年的大面积干旱;唐宝琪等[33]基于安徽省1961—2013年重大旱灾发生年份数据,成功预测了安徽省2016年的干旱;方兰[34]结合贵州省历史干旱数据预测了2013年的干旱。
然而,目前基于可公度性理论的预测普遍存在计算过程烦琐、计算量大、预测结果的判别受人为主观影响较大、不同元可公度式计算结果之间综合评价不够等,一定程度上制约了该方法的应用推广。为此,本研究基于可公度性理论,引入层次分析法(AHP)、MATLAB、SAS软件等进行区域干旱预测,并将预测结果与蝴蝶结构图及前人预测结果进行对比验证,以期提出一种便捷、快速、准确的干旱预测方法,为干旱预警决策提供依据。
1 研究方法
1.1 可公度性理论
1.1.1 可公度预测模型
利用可公度性理论进行干旱等自然灾害预测时,通常采用三元、四元和五元可公度式进行预测[26-27,31],其中:
三元可公度式为:

四元可公度式为:

五元可公度式为:
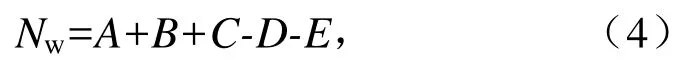
式中:Nu、Nv、Nw为预测的未来时间;NΔ为四元可公度式预测的时间间隔;Ne为历史数据由小到大排列后的最末数据;A、B、C、D、E为选取的历史数据。
1.1.2 可公度式频数计算
可公度式频数是表征干旱发生年份的重要指标。将发生干旱的历史年份按照时间顺序排列,并分别代入式(1)-式(4)进行外推,可求得各可公度式推求的灾害趋势年份及其对应的可公度式频数,频数越高,表明干旱发生的概率越大。本研究采用MATLAB和 R2018b进行可公度式频数计算。
1.2 干旱发生年份预测
传统干旱预测方法是将三元、四元和五元可公度式计算的可公度式频数进行排序,选取频数均相对较高的年份作为预测的灾害发生年份[34-37],但存在受人为主观影响较大及预测结果不准确的弊端。本研究采用层次分析法对三元、四元和五元可公度式频数计算结果进行综合评价,定量评价干旱发生的可能年份。
1.2.1 建立层次结构模型
层次结构模型是将决策的目标、考虑的因素(决策准则)和决策对象按其相互关系分为顶层、中层和底层,本研究目标为干旱预测,决策准则为可公性理论的三元、四元和五元预测模型,决策对象为预测干旱发生年份。
1.2.2 确定定量化的标准
在对三元、四元、五元可公度式及各可公度式频数计算结果进行相互比较时,需要给定定量的标度。本文参考A.L.Saaty提出的标度方法[39],该方法是两两因素相互比较,采用相对尺度,以尽可能降低性质不同的诸因素相互比较的难度,进而提高准确度。
1.2.3 建立判断矩阵
本文根据表1对三元、四元、五元可公度式预测模型及其分别对应的计算结果建立比较矩阵。
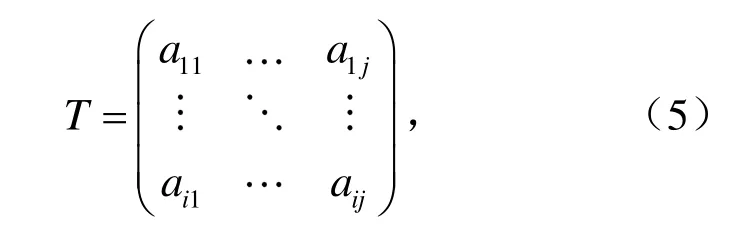
式中:aij为因素i与因素j相比得到的重要性比值。

表1 比例标度表Table 1 Proportional scale table
1.2.4 层次总排序及一致性检验
层次总排序即将三元、四元、五元可公度式预测模型计算的频数权重按预测年份先后顺序分别排序,并对总排序进行一致性检验以确保精度,要求CR值均小于 0.1,即认为矩阵的不一致程度在容许范围之内,可采用其归一化特征向量作为权向量,否则要重新构造比较矩阵。
判断矩阵标准CR采用下式计算:
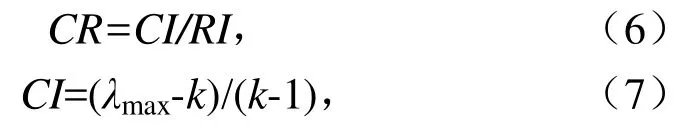
式中:RI为随机一致性指标,通过查询表2求得;λmax为判断矩阵的最大特征值;k为判断矩阵的阶数。
1.3 干旱预测结果的验证
本研究采用蝴蝶结构图法对同期干旱发生年份进行预测,并对上述方法预测结果进行对比验证。蝴蝶结构图法是一种基于等时间间隔反映变量之间多周期变化的方法[34]。蝴蝶结构随机预测概率与可能度对应关系见表3,事件预测的可能性为:

式中:F为用于预测的灾害总数;E为预测中涉及的灾害次数。
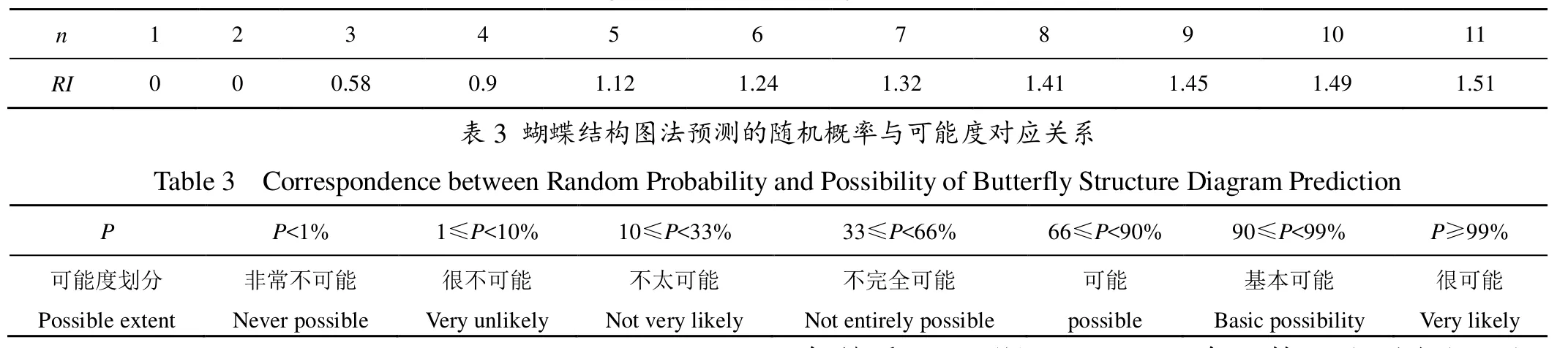
表2 平均随机一致性指标RI标准值Table 2 Average random consistency index RI standard value
2 数据来源
本研究以河南省为例,采用河南省历史发生干旱年份数据进行模型验证和预测。河南省位于我国中东部、黄河中下游,是我国粮食产出大省,受暖温带亚热带、湿润半湿润季风气候和特殊的地貌格局影响,全年温度、降水量变化较大,导致干旱频发且时空分布复杂[39-40],以春旱和夏旱为主,其中中度干旱主要发生在北部和西部地区,重度干旱主要发生在西部和中东部地区[41-42]。

表4 SPEI值干旱等级划分Table 4 Drought classification based on SPEI
依据1961—2016年共计56 a气象资料,按照中国气象局制定的基于降水蒸散指数(SPEI)的干旱等级划分标准(表4),其中1961、1965、1966、1968、1972、1976、1978、1981、1986、1988、1997、2001、2013、2014年共14个年份为严重干旱年份[43]。本研究依据该干旱年份数据进行基于可公度性理论的干旱预测模型验证及干旱预测,根据前13个干旱年份对2014年是否发生严重干旱进行预测,以验证该方法的实用性;进一步采用包括2014年的上述系列干旱年份数据,对河南省2030年前发生严重干旱的年份进行预测。
3 研究结果
3.1 可公度性理论干旱预测模型验证
利用受灾年份,构造可公度集X={1961,1965,1966,1968,1972,1976,1978,1981,1986,1988,1997,2001,2013},即X1=1961、X2=1965、X3=1966、X4=1968、X5=1972、X6=1976、X7=1978、X8=1981、X9=1986、X10=1992、X11=1997、X12=2001、X13=2013,通过式(1)-式(4)计算系列干旱年份中最近干旱年份后10 a(即2014—2023年)的三元、四元、五元可公度式频数,统计结果见表5。由表5可知,2014年四元和五元可公度式频数均为最大,且三元可公度式频数最小,据此可判定该年度河南省发生严重干旱的频率最高,这与实际情况相符。2014年7—8月,河南省严重干旱导致24.5万人、8万头大牲畜发生临时性吃水困难,秋粮受旱面积达154万hm2[44],表明可公度性理论可用于区域干旱年份预测。
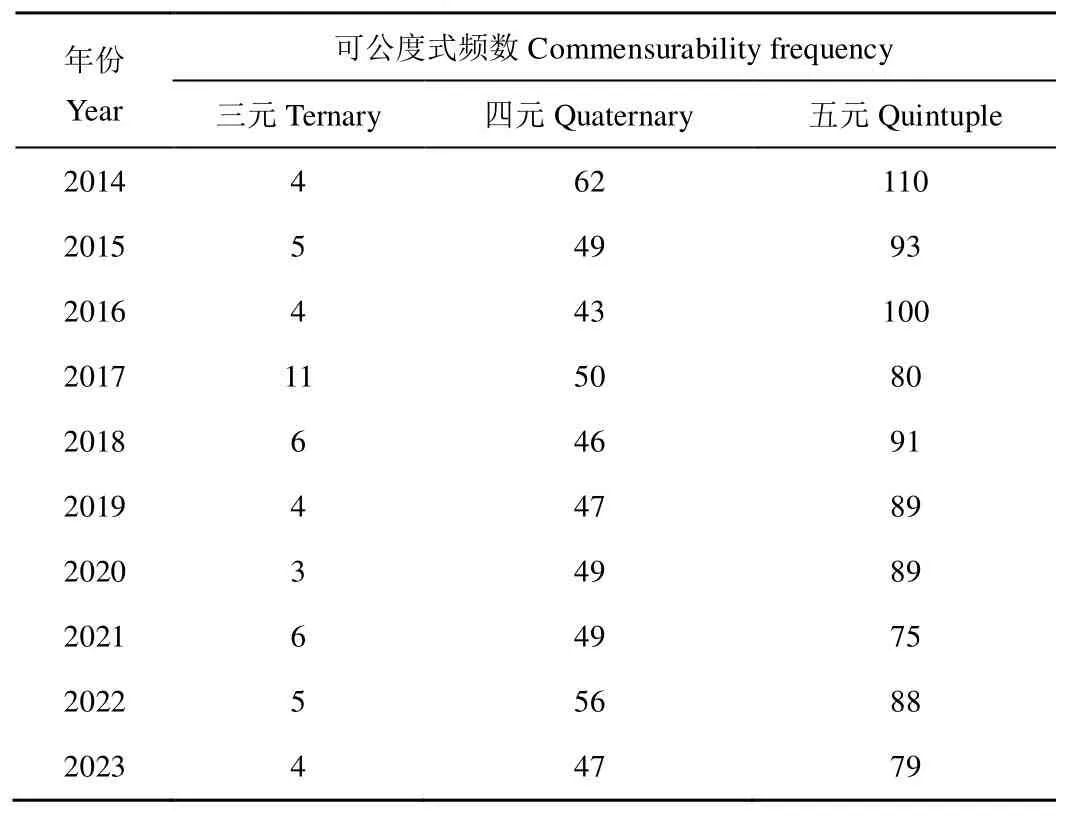
表5 三元、四元和五元可公度式频数计算结果Table 5 Ternary, quaternary and quintuple commensurability frequency statistics
3.2 基于可公度性理论的干旱预测
3.2.1 可公度性理论计算
采用包括 2014年的上述干旱年份数据进行河南省 2030年前干旱发生年份预测,得可公度集为X1=1961、X2=1965、X3=1966、X4=1968、X5=1972、X6=1976、X7=1978、X8=1981、X9=1986、X10=1992、X11=1997、X12=2001、X13=2013、X14=2014,算法同上,2019—2030年可公度式频数计算结果表6所示。
3.2.2 3种预测方式独立性检验
利用SAS 9.4/STAT模块中的FREQ进行r×c联列表的卡方独立性检验,检验结果为P=0.999,由于P>0.05,表明三元、四元和五元可公度式预测模型对受灾年份的预测互不相关,彼此独立,也表明综合考虑3种预测结果的准确性高于单一预测方法的准确性。
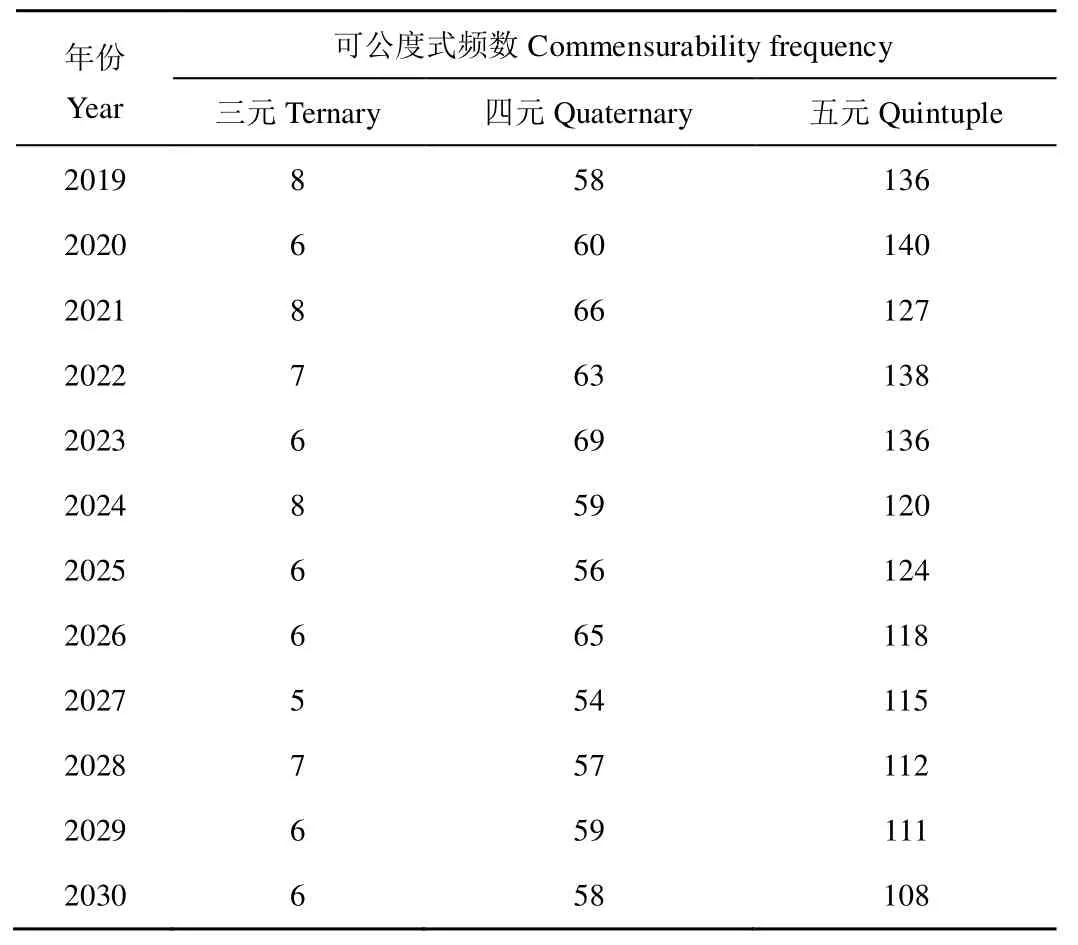
表6 河南省不同预测年份三元、四元和五元可公度式频数计算结果Table 6 Calculation results of ternary, quaternary and quaternary commensurability frequencies for the different predicted years of Henan Province
3.2.3 基于层次分析法综合分析
本研究采用层次分析法综合评价 3种预测方法预测结果。如图1所示,建立层次结构模型,第一层为目标层(α),第二层为指标层(βi),第三层为方案层(γi)。
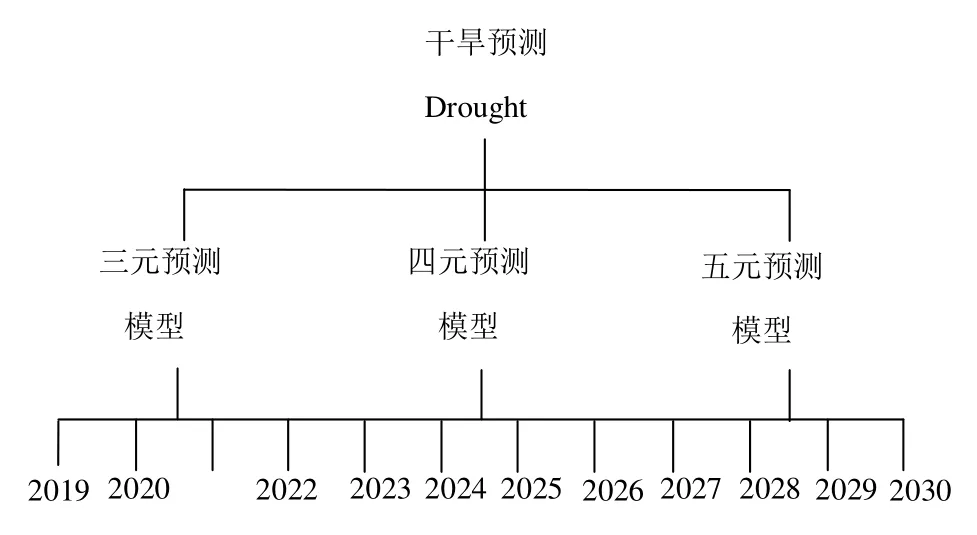
图1 层次结构模型Fig.1 Hierarchical model
β1表示三元预测模型,表示四元预测模型,β3表示五元预测模型;γ1~γ12分别表示 2019、2020、2021、2022、2023、2024、2025、2026、2027、2028、2029、2030年。由层次结构模型、矩阵元素aij标度方法和可公度性理论频数统计,建立α-βi、β1-γi、β2-γi和β3-γi4组判断矩阵,由式(6)计算CR,结果表明各矩阵CR值均小于0.1,表明各矩阵具有较好的一致性。进一步计算得出最终的层次排序总权重,并将其转化为矩阵α、β:

由α*β计算结果可知,γ5为最大可能发生年份,其对应年份为2023年,即河南省2023年可能发生严重干旱。
3.3 基于蝴蝶结构图的干旱预测
蝴蝶结构图的对称分析数据同样选自上述干旱年份序列,1986年作为对称点,相同间隔组为7组,有较好的对称结构。计算结果表明,1961年以来 2、4、10、12、13、16、25 a的准周期显著,据此绘制蝴蝶结构图如图2所示。由图2可知,25 a周期出现了 5次,出现次数最多,2022年参与预测的灾害年份为5个,2023年参与预测的灾害年份为12个。根据式(8)计算得出2022年和2023年河南省发生严重干旱的概率分别为38.46%和92.31%,由表3可知,2023年河南省基本可能发生严重干旱。
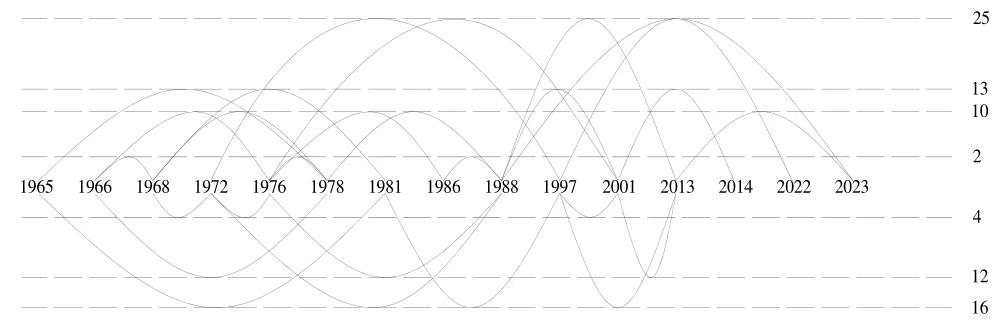
图2 蝴蝶结构图Fig.2 Butterfly structure diagram
4 讨 论
目前,基于可公度性理论的干旱预测方法的应用和推广受计算过程烦琐、计算量大、预测结果的判别受人为主观影响较大、不同元可公度式计算结果之间缺乏综合评价等缺点的限制。为此,本研究以河南省为例,基于可公度性理论,结合层次分析法(AHP)、MATLAB和SAS软件对河南省的严重干旱年份进行预测,得出河南省可能在2023年发生严重干旱;蝴蝶结构图法预测结果同样表明2023年河南省发生严重干旱的概率最高,为92.31%;基于上述2种预测方法一致的预测结果表明2023年河南省发生严重干旱的可能性较大,这与温婷婷[45]利用马尔可夫链预测模型状态转移规律预测、阎苗渊[46]基于灰色灾变及拓扑预测、张功瑾[47]采用小波分析、李俊亭[48]利用综合气象干旱指数-Ci指数等预测结果相似,进一步印证了基于可公度理论的层次分析法在干旱预测方面的实用性和准确性。
本研究仅对基于可公度性理论的干旱预测方法的计算、结果的判定进行优化,目前采用该方法进行干旱预测多数是在年尺度上,本研究亦然,但基于该方法的干旱预测仍缺少在季节尺度和空间尺度上的研究,因此,收集区域干旱其他尺度的历史周期数据、气象数据,并结合该方法进行多尺度的干旱预测,以进一步提高干旱预测的实用性及精确性,为干旱预警提供理论依据。
5 结 论
1)以河南省为例,采用历史严重干旱发生年份数据资料,对基于可公度性理论和层次分析法的区域干旱预测方法进行了模型验证和未来干旱发生年份预测,结果表明,河南省2030年前发生严重干旱的可能年份为2023年,这一预测结果与蝴蝶结构图法及前人预测结果一致,表明该方法在用于区域干旱年份预测时具有较强的实用性。
2)该方法采用MATLAB软件进行数据计算,较传统可公度式频数计算方法节约了计算时间,且层次分析法的应用量化了三元、四元和五元可公度预测模型预测结果的综合分析过程,降低了主观因素对预测结果判别的人为影响,提高了预测结果的准确性。

