充分挖掘教材资源 引导学生深度学习
江苏省常熟市商城小学 钱 萍
在深度学习过程中,为了让学生成为既具有独立性、批判性、创造性又有合作精神、基础扎实的优秀学习者,我们将深入理解教材,充分利用显性资源、隐性资源、特殊资源,处理各种矛盾,关注联结、转换、融通,有效地将学生的思考与体验外显,开启真正意义上的深度学习之旅。
一、深度对话显性资源,在联结中变“要我学”为“我要学”
我所描述的“显性资源”指的是现行苏教版小学数学教科书中编排的例题、练习、“专题活动”、“你知道吗”、“探索与实践”、“动手做”等板块内容。它们构成了有些单薄的数学书,如果碰上“教教材”的老师,确实会觉得降低了工作难度,越教越简单;如果是“用教材教”的老师,则会觉得无形中拓宽了教学空间。因为在课前,首先要进行教材解读,弄清习题与例题的关系,弄懂文本编排的意图,进而扎实组织课堂教学,使单薄书本变厚,简单的题目“变深”。
课堂再现:六上《分数乘分数》
承接上一节课《整数与分数相乘》概括出的核心知识“求一个数的几分之几是多少”用乘法计算,提出“当这个数是分数的时候,分数的几分之几是多少还是用乘法计算吗”?围绕这个核心问题,我们展开一系列的猜想、操作、验证、探究等活动,厘清分数与分数相乘的几何意义及计算方法,拓展了对分数乘法的认识和理解,接着迎来了每课必有的“练一练”。
提问:我们已经掌握了分数与分数相乘的方法,教材为什么还要出现配图,并且帮我们把过程都画好了?
生1:帮助掌握得不太好的同学再次巩固。
生2:给我们检验结果用。
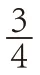
生5:乘法交换律在整数乘法和小数乘法中证实并得到运用,在分数中能适用吗?
鼓励:与其在这里猜测,不如动手画一画,算一算,得出结论。

引导:只要能算出结果就可以了,为什么那么在乎两个分数的顺序呢?能举个例子说明吗?
案例剖析:配图的价值讨论,从培养“我们”的检验意识、形成良好学习习惯等非智力因素,到交换乘数位置后算式意义发生改变,突出本课知识核心,找到比常规算法更深刻的内涵。最后回归知识核心,一个数的几分之几是多少,用乘法计算,这个数可以是整数、分数,也可以是小数。
传统牵引式的“要我学”模式,为什么激发不了学习热情?那是因为没有主动联结,学生在老师一轮又一轮的琐碎问题拷问下,没有了解知识内在的组织结构。案例中,我们用建构方式学习结构中的知识,使“知识的内在秩序”与“学生的认知顺序”得到有效对接,知识由“客观静态”走向“动态生成”,由“零散”走向“结构”,由“模糊”走向“清晰”,由“要我学”走向“我要学”。
二、深度对接隐性资源,在转换中变“不会学”为“我会学”
我所理解“隐性”资源即指没有外在表现但确实有其内容的学习资源。这些资源往往是融合在教学,尤其是在旧知引入新知的跨越和新知核心的理解及拓展等方面。每个教师对于课程资源开发的见解不同、自身能力结构多元,我们要依据自身的能力,用合理的方法组合内隐条件,开拓内隐性素材的课程资源。教学中,教师可以通过整合教学资源,创设相应的教学情境,促使学生提出相关联的问题,顺着问题加深对数学本质的认知和理解,展开相关预判、尝试,使学习步骤很自然地“紧凑”起来。
课堂再现:六上《百分数和小数的互化》《百分数和分数的互化》
情境创设:学校田径队进行体能训练,李老师要求队员用5 分钟完成指定个数的仰卧起坐练习,如果你就是其中一个队员,你能否完成任务呢?
鼓励:能用一个学过的数表示这个结果吗?
①具体完成了几个;
②用小数表示是否完成;
③用分数表示完成情况;
④用百分数表示完成情况;
讨论表征方法的合理性,得出方法①不能以“我”平时测试成绩为标准,要以教练“指定个数”为准。其他三种方法都能顺利表征结果,因为它们都把“指定个数”看作单位“1”,用不同的方式表示与单位“1”的关系。
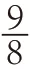
案例剖析:我将两课时内容的两个情境统整为一个情境,但并不表示我将两个课时压缩成一课时进行赶进度式的教学。引导学生在“充裕”的环境氛围中构建起一张“紧凑”的知识网,并教给了学生“打包”知识的方法,这一切都源于小数、分数、百分数之间密切关联的相对内隐的网状资源。
巧妙的转换就在情境引发的一系列问题中悄悄进行,与之一道生长的还有新知的内化和生长,当然最重要的是逐渐强烈的问题意识,学习个体由之前的“不会学”本能地向“我会学”自然转变。
三、深度操作特殊资源,在融通中变“假学习”为“真学习”
“暗示”是一种老师青睐的教学手段,为了能够顺利完成课前预设,我们很多时候会将教学内容、学习方法甚至是数学思想作铺垫,减少坡度,使学生的探究过程十分顺利,在下课铃声响起的那一刻,正好完成既定的教学任务与目标。脱离这种非正常的“铺垫”,我们的数学课堂是不是真的探究不起来,或者说因为在探究环节耗费过多的时间而使整堂课上不完整?没有真正的、充分的探究的课,是一种“假学习”,是没法培养学生深度学习能力的。任何一种能力素养的养成都是要从小培养的,低年级学生主动联结能力、推理能力都还较弱,是不是就更不适合开展深度教学,或者教学根本就无法深入呢?听了本校章老师的一节课,让我豁然开朗。
课堂再现:二年级《认识线段》
章老师带领学生认知线段基本特征之后,课件动画演示如图1 的操作:

图1
第一层要求:折跟老师一样长的线段如图2。

图2
追问:你确定第二根线段跟老师的一样长?(学生回答:转一下就一样了;它跟边一样长,老师的也和边一样长)
提问:跟老师一样长的找到了多少?(呈现学生作品,竖和横方向许多条)
提问:这么折下去折得完吗?
第二层要求:还想折吗?(学生提出:要折一条比老师折的长的线段)
学生折出正方形的对角线(见图3),理由是斜的要比直的长。

图3
追问:还有更长的吗?学生表示凭感觉其它斜线都比这条短。
第三层要求:还想折吗?(学生提出:要折一条比老师刚开始折的短的线段)
学生呈现如图4 两种,老师问:一眼能看出来它们都比老师的短,谁更短呢?
老师话刚落,旁边的学生就从老师的手里拿下两张纸,重新折好,重合后比了比,马上把更短的一条举在手里。
案例剖析:这是老师找准“线段有长短”这一特性为切入点,加工创造的一个教学环节,像这样的资源,不能从书本中找到原形。老师准确把握教材内容的深度和广度,找准合适的切入点,在一些操作材料、实验器材、生活经验等辅助下实现对知识的深度探究,这种资源可归为整合性的特殊资源。本案例中,章老师借助一张彩纸,通过三个挑战性问题跟学生展开对线段特性的探究。初始层次探究中,透露出学生已经有“旋转一个图形,旋转后图形的大小形状不变”的直觉意识,萌发了借助中间线段进行等量替换的推理萌芽,初步体验极限思想。第二层次探究时,依靠学生的经验积累和直觉思维,引导学生作出大胆判断,并进行合理引导。通过层层探究,学生获得了丰富的探究结论,最后概括提升发现“线段有长有短”这个重要结论。学生不满足于此,主动地提出要折更长更短的线段,并且通过交流对话、实验操作将思考和想法外显出来,这种举一反三的创意和灵感正是深度学习中倡导的个性化表达,个性化发展,原先所关注的孩子能力与意识的方面其本身并没有缺失,是我们的“假学习”将这些能力扼杀掉了,与其费力地唤醒与培养,不如客观尊重和良性引导来得更加合适。当学生的学、思、悟、行成为一个紧密联系的整体时,说明他们进行的是“真学习”。
数学课堂中,肯定不止对以上三种资源的深度开发与利用,我们可以触碰到的资源十分丰富,比如还有生成资源、错误资源、作业资源等。可以感受到的是深度学习来自我们的日常课堂,来自教师对教材的理解、感悟和熟练地驾驭,是对日常课堂的品质提升,是能促进学生不断自我构建数学体系、体会思考乐趣,逐步学会学习、享受学习,达到良好学习状态的一种模式。

