结合DBSCAN聚类算法和粒子群算法的大规模路径优化方法研究

丁 乔，李 旭，王建春 DING Qiao, LI Xu, WANG Jianchun

（山东科技大学 交通学院，山东 青岛266590）

0 引 言

随着电子商务的迅猛发展，物流行业迎来难得发展机遇的同时也面临着巨大挑战，现代物流业发展的目标是在满足客户需求的同时降低运作成本，但配送环节的成本占比最高且居高不下，成为阻碍物流发展的一个瓶颈。为了有效地组织配送业务，Dantzig 等[1]将配送过程抽象化，于1959年提出了车辆路径问题（Vehicle Routing Problems, VRPs）。从此大量的国内外学者对车辆路径问题进行了广泛且深入的研究，并且取得了丰硕的成果。目前VRPs 问题的求解规模一般为数百个客户点，但在实际配送实例中该问题的规模远不止如此，比如在上海，菜鸟驿站每天有大约30 万个包裹需要配送，这些问题的规模往往成千上万。VRPs 问题是一个典型的NP-hard 问题，求解大规模的车辆路径问题具有很大的挑战性。

车辆路径优化问题属于NP-Hard 问题，一经提出就引来大批国内外研究人员的深入探索，如今对于此问题的研究主要集中在车辆路径优化模型的建立[2-4]和车辆路径优化模型求解算法的研究[5-8]，通过对建立车辆优化数学模型的深入研究使得车辆路径优化问题越来越多样化，越来越符合最后一公里的配送实际；通过对模型求解算法的研究，使得模型的求解速度和精度不断提高，已达到能够更好解决这个NP 难题的目的，但目前对于大规模的车辆路径问题研究相对较少，其中：王文蕊[9]通过地理信息的分级管理实现车辆路径问题规模的降低，最后通过济南市区卷烟配送对提出方法进行验证。冉崇善[10]将该问题分为两个阶段进行研究，分别为利用基于基地启发式分区算法进行区域划分和利用改进的遗传算法来确定具体的一条配送线路的先后次序，完成配送路径优化任务。马汉武[11]在大规模车辆路径问题引入装卸频率的概念后，建立优化模型并设计改进混合遗传算法进行求解。由上述文献可知，广大学者对于大规模车辆路径问题的研究主要是从如何将其规模降低的角度来进行思考和解决的。本文提出一种结合自适应DBSCAN 聚类算法的路径优化方法，通过DBSCAN 将客户点形成若干个聚类簇，将大规模的城市果蔬配送路径优化问题转换成常规的路径优化问题，然后通过粒子群算法进行求解，完成路径优化。

1 自适应DBSCAN 聚类算法

DBSCAN 是基于密度空间的聚类算法，与K-means 不同，它不需要确定聚类数量，由数据聚类结果显示聚类数量，并且其可以用于凹数据集，适合用于不规则分布客户点的聚类分析。DBSCAN 需要确定两个参数：Eps为在一个点周围邻近区域的半径；MinPts为邻近区域内至少包含点的个数。Eps的选择根据实际问题而定，MinPts的选择通常采用k-距离图像法来确定。本文采用一种自适应DBSCAN 聚类分析方法，通过利用数据集自身分布特性生成候选Eps和MinPts，自动寻找到聚类簇数量变化的稳定区间，此时对应的参数即为要选择的最优参数。但是文献[12]中的方法计算量巨大，适合用于样本数量较少的情况，对于样本数量巨大的情况该方法所需的计算时间会显著增加。因此本文对该方法进行了改进，将Eps和MinPts候选参数的选择由全局取期望值改成了抽样取期望值，具体步骤如下：

步骤1：计算数据集D的距离分布矩阵[13]，n为样本大小，即：

步骤2：对距离矩阵Dn×n的每一行元素进行升序排列，则第i列的元素随机取x个组成Di。

步骤3：对Di中的所有元素取平均数对所有的i值进行计算，最终得到Eps参数候选列表DEps：

步骤4：生成MinPts参数候选列表DMinPts，在数据集D中随机选取x个对象，对于步骤3 得到的Eps参数候选列表DEps，依次计算每一个DEps列表中的Eps候选值的领域对象数量，并计算对象数量的数学期望，作为数据集D的邻域密度阈值MinPts参数，即：

式中：Ni表示第i个对象的Eps邻域对象数量，x表示从数据集D中随机抽取的对象数。

步骤5：依次选用DEps列表和DMinPts列表中的元素作为Eps和MinPts参数，输入DBSCAN 算法中对数据集进行聚类分析，分别得到不同输入参数下对应的聚类簇数，当聚类簇数连续3 次相同时，认为聚类结果趋于稳定，记该聚类簇数为最优聚类簇数M。

步骤6：继续执行步骤5，直到聚类簇数不为M，则选择最后一次聚类簇数为M时对应的Eps和MinPts为最优参数。

2 路径优化模型及求解算法

2.1 路径优化问题建模

本文所研究的城市生鲜配送车辆路径优化问题，可以看做是带时间窗的车辆路径问题（Vehicle Routing Problems with Time Windows，VRPTW），以车辆的最大载荷和客户的时间窗为主要约束，目标函数由固定成本、运输成本、制冷成本和惩罚成本四部分组成，如公式（4） 所示：

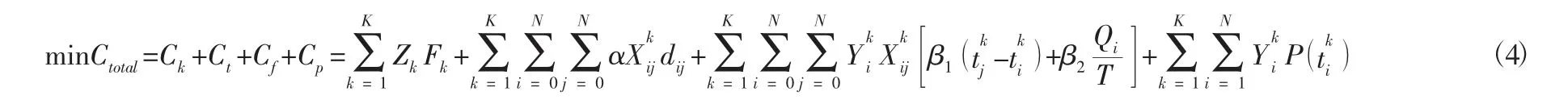
约束：

其中：式（5） 表示每个客户点只能有一辆车为其服务；式（6） 表示每辆车的载重不能超过最大载荷；式（7） 表示到达客户点的车和离开客户点的车数量相同。

其中参数和决策变量的含义如表1 所示。

2.2 粒子群算法

粒子群算法（Pariticle Swarm Optimization，PSO），PSO 的优势在于简单容易实现，同时又有深刻的智能背景，既适合科学研究，还特别适合工程应用，并且易于实现、收敛速度快和没有许多参数需要调整。一经提出就被学术界广泛关注，集中针对PSO 中的参数调整优化和种群结构改进以及与其他职能算法相融合等方面进行了深入的研究[14-17]，近些年粒子群算法也被广泛的应用于物流最后一公里的配送问题中。

表1 参数及决策变量表

将PSO 应用于物流最后一公里配送中，则问题的求解目标即为配送所产生的的成本最小，每一个粒子表示一种可行的配送方案，通过PSO 算法的迭代规则，最终找到配送成本最低的配送方案。粒子群算法的一般数学模型：假设在N 维空间进行搜索，粒子i 的信息可用两个N 维向量来表示：

式（8） 表示第i 个粒子的位置。

式（9） 表示第i 个粒子的速度。粒子通过以下式子来更新自己的速度和位置：

其中：

N 是粒子长度，即解空间的维度；

i=1,2,3,…,M是种群大小；

c1和c2是学习因子，又称加速系数；

rand1和rand2是介于［0,1 ］之间的随机数；

Pbes是粒子i在第k次迭代中第d维的个体极值点位置；

Gbes是整个粒子群在d维的全局极值点的位置。

3 案例分析

本文选取了青岛市黄岛区1572 个餐饮店作为配送点，配送中心选择当地已有的生鲜批发市场，通过本文的方法先对这些餐饮店进行聚类分析，将大规模的路径优化问题简化成正常规模的路径优化问题，然后建立路径优化模型并利用粒子群算法完成对这1572 个客户点的配送任务。

图1 为餐饮店的分布图，由图1 可知餐饮店的分布具有一定的规律性，具有集中分布的特点，但是有一些分布区域集中的餐饮店数量巨大，不利于进行路径优化计算，所以需要采用自适应DBSCAN 算法对餐饮店进行聚类分析，利用餐饮店之间的位置空间关系，将餐饮店进行分类分区域。

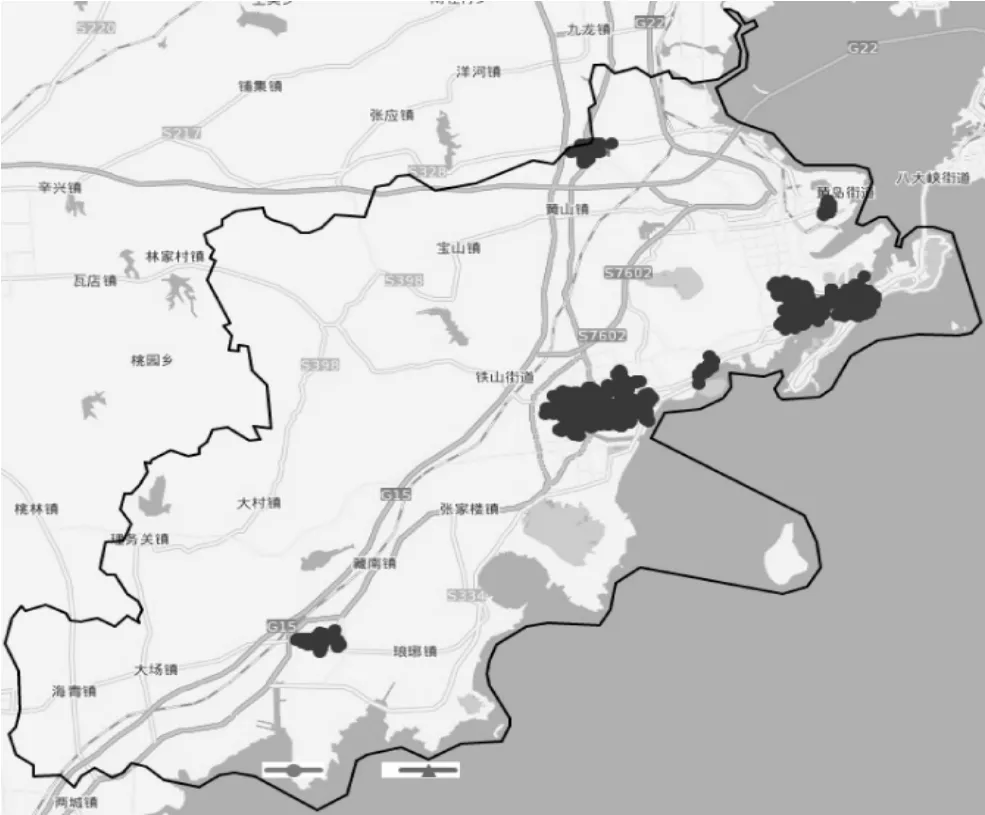
图1 餐饮店分布图

图2 参数序列与聚类簇数折线图

通过本文的自适应DBSCAN 候选参数选择方法，得到MinPts和Eps参数列表，将参数列表中的参数对逐个代入DBSCAN算法，得出对应的聚类簇数，如图2 所示，由图3 可知在第19、20、21 组参数得到的聚类簇数连续3 次都为8 个，第22 组为6 个，依据本文的方法选出最优MinPts为68，最优Eps为1118.29m。聚类结果如图3 所示。不同的颜色表示不同的聚类簇，其中会有少量的噪声点，本文处理的方式是将噪声点归入就近的聚类簇。各个聚类簇成员数量如表2 所示。

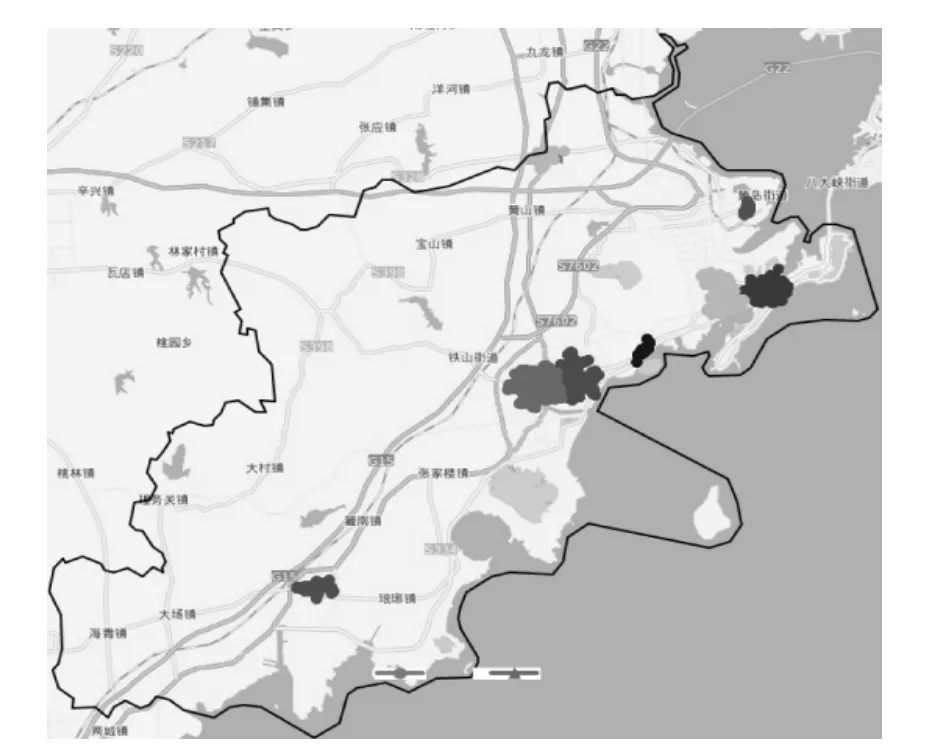
图3 聚类结果显示

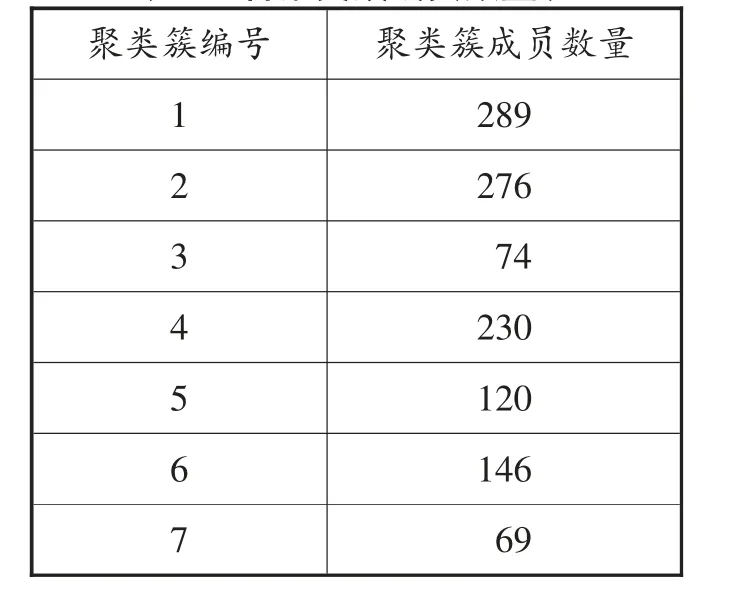
表2 各聚类簇成员数量表

为了验证该研究方法和数学模型的可行性，选择当地的薛家岛农贸批发市场为配送中心，以聚类簇1 的餐饮店为配送客户点来完成配送任务。采用Matlab 编程实现粒子群算法，所建立的路径优化数学模型进行仿真计算，仿真结果如图4 所示，其中编号0 表示配送中心，其他客户点编号为1-289，本次任务一共使用了14 辆配送车辆，总成本为2680.7562 元，计算所用时长为16 秒，每辆车具体的配送路径如表3 所示。

图4 路径优化结果展示

表3 车辆配送路径表

4 结 论

该研究将自适应DBSCAN 聚类分析算法和粒子群聚类算法相结合，通过使用聚类分析算法将配送客户点进行分类，将大规模车辆路径优化问题转变为正常规模车辆路径问题，然后根据生鲜农产品配送的实际情况建立生鲜农产品配送路径优化模型，使用粒子群算法对模型进行求解，对解决大规模车辆路径优化问题提供了新的解决方案，丰富了车辆路径优化问题的解决理论。最后通过青岛市黄岛区1572 个餐饮店进行实例验证，证明了本研究方法的可行性和合理性。