基于驴与走私者算法的物流配送车辆路径优化研究

王 迪 金 辉

(辽宁工业大学汽车与交通工程学院 辽宁 锦州 121001)

0 引 言

物流配送车辆路径优化作为物流运输系统的核心问题[1]，也是提高物流配送效率和降低物流成本重要途径，一直以来受到各方的重点研究[2]。物流配送车辆路径问题主要是指物流车辆从配送中心出发，将货物送到各个配送点最后返回配送中心，并且在满足各种约束条件下形成的最优车辆配送路线方案[3]。车辆路径优化问题(VRP)是广泛存在于实际生活与工程中的经典离散组合优化问题，已被证明为NP-hard问题[4]，找不到一个多项式时间算法来精确地求解其最优解[5]。因此利用智能优化算法求解VRP问题，已经成为该领域的研究热点。常用的求解VRP问题的智能算法包括遗传算法[6](GA)、蚁群算法[7](ACO)、粒子群算法[8](PSO)、模拟退火算法[9](SAA)、布谷鸟算法[10](CS)等。上面提到的群体智能算法都是受到各种动物和昆虫的不同社会行为的启发，以解决各种优化问题。然而，没有任何一种群体智能算法可以解决所有优化问题。在上述提到的算法中，ACO非常受欢迎，它设计目的是为了解决组合优化问题，主要通过搜索成本最低或距离最短来解决问题。但是，它有一些局限性，如理论分析不容易，概率的分布会随着迭代次数的改变而改变，并且收敛的时间不确定。

因此，本文将采用一种新兴的智能算法——驴与走私者算法[11]对VRP问题进行求解研究。驴与走私者算法是Shamsaldin等[11]在2019年提出的一种新型路径查找的协作工作方法，并在理论上证明此算法可以用于求解旅行商问题(TSP)、数据包路径(PR)和救护车路径规划问题(AR)等，且取得了不错的效果。因此，本文将DSO算法运用到求解物流配送车辆路径优化中，具有实际的研究意义。

DSO算法是受到驴的搜索行为的启发，通过在走私过程中模拟驴的运输行为，从而建立两种模式(非自适应和自适应)来实现算法中的搜索行为和路径选择。DSO算法是基于种群的算法，这里的种群是指在算法的自适应部分中使用的解决方案组。在其他基于种群的算法中，例如遗传算法，是通过不断在不同的解决方案中进行交叉和变异操作，从而获取最佳解决方案。但是，在DSO算法中，由于走私者会探索所有解决方案并计算其适用值大小，因此无需进行此类处理。再将这些解决方案放入一个总体中，并从总体中确定最佳解决方案。在算法的自适应(驴)部分中，将继续维持第一部分中求解的最佳方案，如果其适应性发生变化，那么将继续评估种群并根据算法程序更新最佳解决方案。

1 基本车辆路径优化问题(VRP)

VRP可以描述为：有n多个需求点，各个需求点之间的距离已知，因此企业需要提前安排规划，通过安排合理的配送路线，将货物配送到每一个顾客的手中，然后再返回到出发点。在此过程中要保证配送过程中路径距离最短或配送成本最低[12]。

模型假设：客户点的数量为n，节点i与节点j之间的距离设为dij，则VRP问题的目标函数和约束条件分别为：

(1)

(2)

(3)

(4)

(5)

(6)

式(1)表示配送路径距离最短；式(2)表示当xij=1时访问节点i后访问节点j，xij=0时则相反；式(3)表示每次配送过程中车辆都要从起点出发；式(4)表示配送车辆在完成配送任务后返回出发点；式(5)表示车辆在进行货物配送过程中，所有的客户点都会被服务到；式(6)表示在配送服务过程中，每个客户点都会有一辆配送车辆进行服务，而且仅能被服务一次[13]。

2 驴与走私者算法

2.1 驴的社会行为

驴具有一系列的社会行为，在一定程度上可以将它们与其他动物区分开来，例如具有良好的记忆力和快速轻松学习的能力。《驴保护区》[14]指出，驴的学习能力可以与狗或海豚一样强。这些特征使驴成为多年来国内和国际走私活动中的第一大走私动物。Diaz[15]指出，走私者使用马、骡子和驴子开展走私业务，如图1所示。

图1 走私者利用驴进行汽油走私

正如Diaz[15]指出的那样，走私者骑着马，用驴或骡子装载了他们想要走私的物品。他还强调，在熟悉的道路上，驴和骡子可以独立地进行走私活动，而无需走私者的指导。在《阿拉伯新闻》[16]的一篇新闻中写道，驴被用来在也门和沙特阿拉伯之间走私杂草，驴是经过驯养者训练的，它们在也门的村庄进行培训，走私者在村庄里穿上沙特边境警察的制服，并开始用石子来攻击驴，从而使驴可以识别这些制服并避开这些制服，即驴会改变方向或一旦识别出这些制服便逃离。

而且，驴还具有较高的地域特征，它们通常单独生活或两个一组生活[14]。每当驴子感受到危险时，逃离并非总是生存的最佳选择，它们的战斗和防御行为将会被触发，从而来保护自己。还有区别驴的另一种行为是自杀，Pubby[17]显示，当驴遭受主人的残酷和残忍的虐待时会选择自杀。

此外，驴子还表现出相互支持的行为。美国广播公司新闻[14]显示，如图2所示，一头驴试图越过栅栏，但它无法跨越，因此它从另一头驴那里得到了帮助，后者摘下一块木头来帮助驴群穿过栅栏。

图2 驴群在同伴的帮助下跨越栅栏

总而言之，驴具有的社会行为可以总结为：

(1) 逃避过去能使它们痛苦的人或经历事件。

(2) 在它们感到危险时战斗或防御机制将会被触发。

(3) 当遇到困难或需要帮助时会互相支持。

(4) 当情况达到驴再也无法忍受的程度时将会自杀。

2.2 DSO算法

根据2.1节，驴的行为可以归纳为以下几点：逃离、面对和支持、面对和自杀。

驴与走私者算法就是通过模拟驴和走私者的行为，利用“走私者”和“驴”的一些行为构造了一个由两部分组成的算法，可以寻找到最佳解决方案并且能够对任何发生变化的情况作出反应以维持最佳解决方案。

2.2.1 非自适应(走私者)

“走私者”部分是DSO算法的非自适应部分，这表示此部分不适应任何更改。在这一部分中，走私者将检查从源头到目的地的所有可能路线，然后根据某些度量(例如时间、路线的安全性和状况等)来决定要采取的最佳路线以及用此路线来进行驴的走私活动。

首先要确定每个解决方案的参数，然后再利用式(7)计算每个可能解的适用度值，并根据每个可能解的适应度值将所有可能解进行分组。最后选择其中适应度最小的作为最佳的解决方案，并根据该解决方案来发送驴。

(7)

式中：xij是可能的解;i是可能解的数量;j表示的是与每个可能解的参数的数量成正比;z表示与每个可能解的参数的数量成反比。分子包含与比例成正比的参数，分母包含与比例成反比的参数。

2.2.2 自适应(驴)

在自适应(驴)部分中，决策基于当前网络状态，即拓扑和流量的测量或估计。如果流量和拓扑都发生变化，或者其中一种发生变化，则会作出反应以避免路径丢失或避免延迟。此反应将基于驴的行为。

首先，使用走私者部分确定的最佳解决方案。其次根据适应性评估当前解决方案(在适应性发生变化的情况下，将继续利用适应性函数以找到更好的解决方案)。接着判断当前解决方案是否有拥塞现象，如果有则需要采取以下步骤：

(1) 逃离：重新评估可能的解决方案总体的适用性并更新最佳解决方案。此行为是将当前路径更改为另一个最佳路径(最佳解决方案)，即当在算法的非自适应部分中确定的最佳解决方案不再是最佳解决方案时，它将被丢弃，并根据新变化设置新的最佳解决方案。

(2) 面对和自杀：修复当前正在使用的最佳路径(优化最佳路径)。同时，删除当前路径并使用另一种最佳解决方案，修复被阻止的可能解决方案，对可能的解决方案总体的适用性不必进行重新计算。

如果由于影响算法适应性的任何更改而在算法的第一部分中设置的最佳解决方案不再是最优解决方案时，那么我们先保留该解决方案。然后将该解决方案放回其原来状态，直到可以利用解决方案集中第二优的解决方案为止。

最佳解决方案的适应度值是解决方案总数中最小的。因此，我们将所有可能的解决方案适应度值减去最佳解决方案的适应度值，将差异最小的可能解决方案视为新的最佳解决方案。通过式(8)，我们可以在其他解决方案中的第二优的解决方案作为最佳解决方案。对于其他可能的解决方案总体的适合性不需要进行重新评估。

bestSuicid Solution=f(xi)-f(bestSolution)

(8)

式中：i是可能解决方案的数量。

(3) 面对和支持：当走私者设定的最佳解决方案中开始出现拥塞或超载的迹象时，我们可以通过在解决方案集中分配次优解决方案来执行相同的任务，从而避免丢弃该解决方案，直到拥塞或超载的迹象都消失。即我们可以使用两个通道来减少拥塞或过载，而不是使用一个通道来发送和接收数据。

当最佳解决方案的路线出现过载时，利用第二优的解决方案进行替代，直到原始的最佳解决方案恢复到正常状态为止。其中不需要对可能的解决方案总体的适用性进行重新评估。

secondbestSolution=f(bestSolution)-f(xi)

(9)

bestSupport Solution=bestSolution+secondbestSolution

(10)

式(9)表示通过从最佳解决方案的适用度值中减去可能解决方案的适用度值来确定哪个解决方案将用作第二优的解决方案。然后，通过式(10)将最佳解决方案与次优解决方案结合起来，以生成使用两条路径来执行同一项任务的最佳支持解决方案。

2.3 DSO算法流程

DSO算法的求解步骤如下：

第一部分：非自适应(走私者)。

(1) 确定每个解决方案的参数。

(2) 利用式(7)计算每个可能解的适应度值。

(3) 选择最佳解决方案并用此方案发送驴。

第二部分：自适应(驴)。

(1) 使用第一部分选择的最佳解决方案。

(2) 利用式(7)评估当前解决方案的适应度值，如果其适应值发生变化，则继续利用适应度函数功能寻找最优的解决方案。

(3) 判断当前最优解决方案是否有拥塞现象，如果存在，则需要执行以下步骤之一：

① 逃离：利用式(7)重新评估可能解决方案的适应度值，选择适应度值最低的可能解决方案作为最佳解决方案。

② 面对和自杀：利用式(8)可以在所有可能解中选择第二优的解决方案作为最佳方案。

③ 面对和支持：当最佳方案出现过载时，利用式(9)在可能方案集中选择第二优的解决方案来支持最佳解决方案。然后利用式(10)将最优解决方案和次优解决方案结合起来，生成使用两条路径执行同一任务的最佳支持解决方案。

DSO算法的执行流程如图3所示。

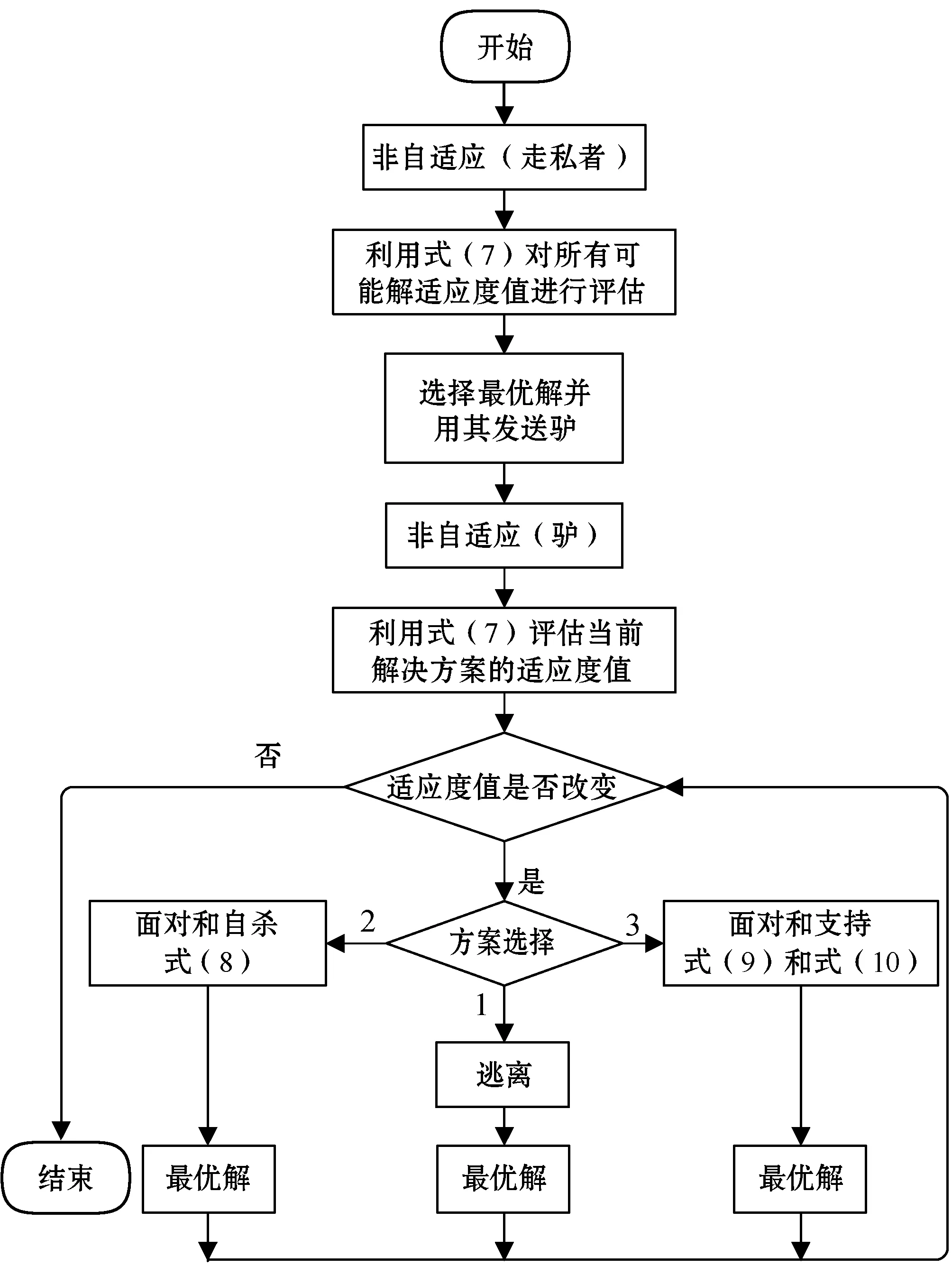
图3 算法的执行流程图

3 实例研究

3.1 问题描述

京东“211限时达”(俗称“当日达”)，即当日上午11点前提交的现货订单(以订单进入出库状态时间点开始计算)当日送达；夜晚11点前提交的现货订单第二天送达。京东开展此业务的目的是为了打通和扩展地区物流配送能力，提高物流配送效率，同时让当地消费者能够享受京东提供的优质电商体验。对于辽西地区来说，京东的“211限时达”业务服务范围已经扩大到锦州、葫芦岛、盘锦、阜新、辽阳、赤峰、朝阳、凌海等县市区。图4为辽西主要城市地理位置图，表1为各个城市之间的距离，其中序号1到8分别代表锦州、葫芦岛、盘锦、阜新、辽阳、赤峰、朝阳、凌海。

图4 配送城市区域图

为了保证货物及时准确地送到各个城市点，京东送货员在接到物流配送任务后，先要制定相应的配送计划和合理的车辆行驶路线，然后按照制定好的行车路线进行配送。送货员需要对其负责的辽西区域很熟悉，如果遇到异常情况，如交通堵塞或者限行，可及时调整行车路线[20]。

表1 各个城市点之间的距离 km

3.2 实例应用

利用DSO算法求解上述问题。对于DSO算法的第一次迭代，在算法的第一部分走私者检查两个城市之间的所有距离，并根据他的经验，确定从每个城市出发的最短路径。每次迭代都重复此步骤，以确定从不同城市开始访问其他所有城市的最短路径。算法的第二部分中，在指出出发节点和要访问所有城市点的最短路径后，搜索并建议新的可能路径，以防止第一部分确定的最短路径不再可用。

算法的第一部分将每个城市点视为一次出发点，并执行了所有迭代以找出所有可能路线及其距离以及要遵循的最短路径。图5为DSO算法第一部分(走私者)求得的最佳路线图。

图5 从每个出发点访问其他客户点的最短路径

其中，第一部分执行时间为0.059 395秒，下面列出了从各个出发点经过的最短路线和其最短距离(单位：km)。

从城市1出发：1 4 5 2 7 3 8 6 1 距离：256

从城市2出发：2 5 4 1 6 8 3 7 2 距离：256

从城市3出发：3 8 6 1 4 5 2 7 3 距离：256

从城市4出发：4 1 2 5 6 8 3 7 4 距离：295

从城市5出发：5 2 1 4 8 6 7 3 5 距离：284

从城市6出发：6 1 4 5 2 7 3 8 6 距离：256

从城市7出发：7 3 8 6 1 4 5 2 7 距离：256

从城市8出发：8 6 1 4 5 2 7 3 8 距离：256

算法的第二部分是在第一部分中选择的最短路径不再可用的情况下，维护通往所有城市点的路线。这一部分中，确定出发节点并确定最短路径后，该算法将扫描整个数据集，并计算出从该节点访问集合中所有城市点的所有其他可能路径及其距离，如图6所示。

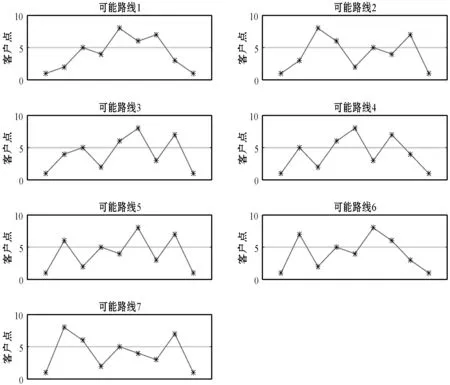
图6 从节点1出发的所有可能路径及距离

第二部分的执行时间为0.025 490秒，下面列出了从城市点“1”出发的可能路线和其经过的距离。

从城市1出发：1 2 5 4 8 6 7 3 1 距离：286

从城市1出发：1 3 8 6 2 5 4 7 1 距离：323

从城市1出发：1 4 5 2 6 8 3 7 1 距离：281

从城市1出发：1 5 2 6 8 3 7 4 1 距离：300

从城市1出发：1 6 2 5 4 8 3 7 1 距离：292

从城市1出发：1 7 2 5 4 8 6 3 1 距离：315

从城市1出发：1 8 6 2 5 4 3 7 1 距离：316

为了比较算法的性能，本文利用ACO算法独立运行求解20次，运行结果如表2所示。

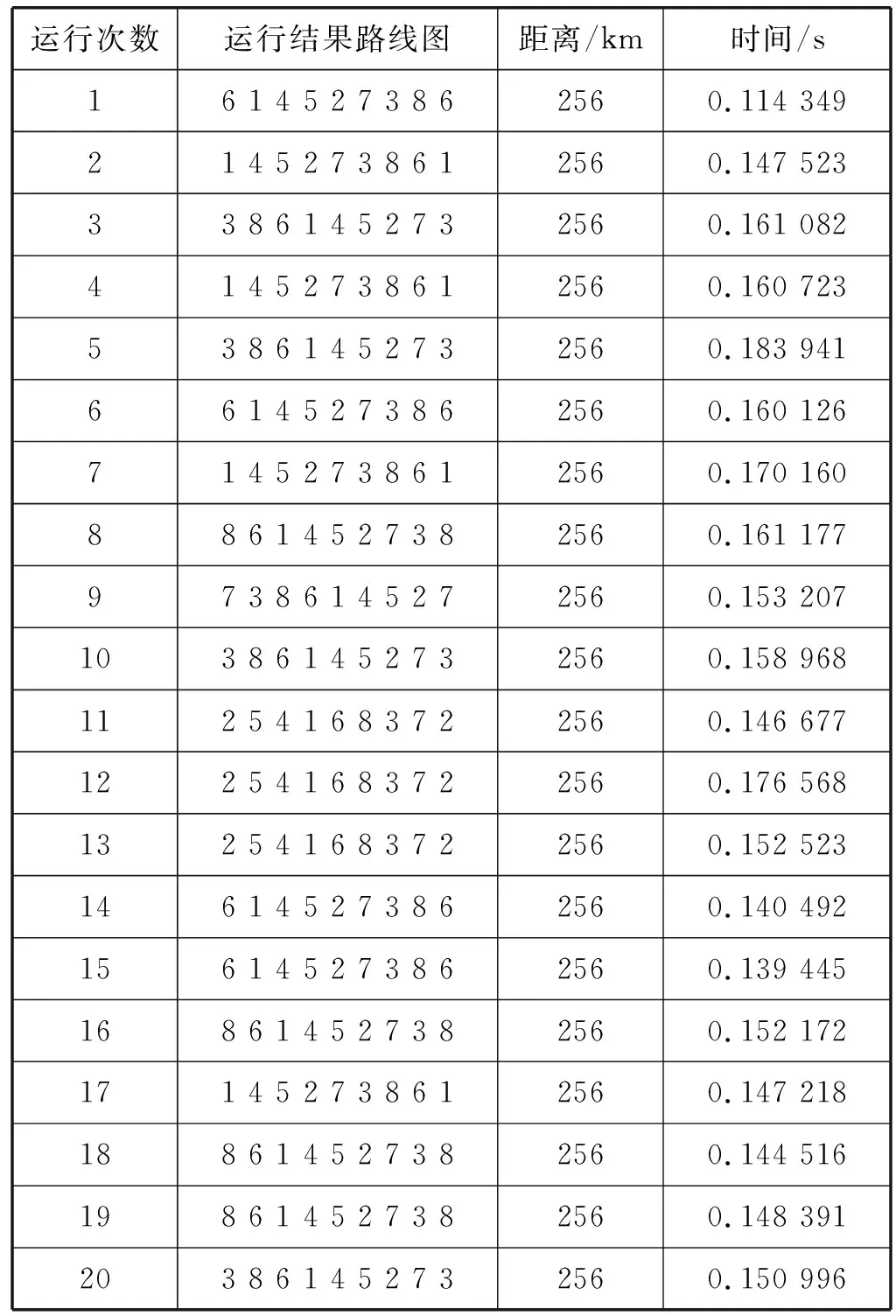
表2 ACO算法运行20次结果

3.3 结果分析

DSO算法的第一部分求解了从每个城市点出发的最佳路径，从城市点1、2、3、6、7、8出发的最佳路径的距离相同，都为256，因此我们可以在算法的第二部分中选择点1、2、3、6、7、8作为出发点。在ACO算法运行20次的结果中，所有路线的最短距离相同，但是起始点却不相同，在20次执行结果中，起始点为1、3、6、8的点出现4次，起始点为2的出现3次，起始点为7的出现1次。

因此，我们可以在DSO算法的第二部分中，选择城市点1、3、6、8作为起始点，DSO以其中一点为起始点计算出所有其他可能的路径。如果选择城市点1作为起始点，则其他可能路径为：

从城市1出发：1 2 5 4 8 6 7 3 1 距离：286

从城市1出发：1 3 8 6 2 5 4 7 1 距离：323

从城市1出发：1 4 5 2 6 8 3 7 1 距离：281

从城市1出发：1 5 2 6 8 3 7 4 1 距离：300

从城市1出发：1 6 2 5 4 8 3 7 1 距离：292

从城市1出发：1 7 2 5 4 8 6 3 1 距离：315

从城市1出发：1 8 6 2 5 4 3 7 1 距离：316

如果选择点3作为起始点，则其他可能路径为：

从城市3出发：3 1 4 5 2 6 8 7 3 距离：269

从城市3出发：3 2 1 4 5 6 8 7 3 距离：280

从城市3出发：3 4 1 2 5 6 8 7 3 距离：288

从城市3出发：3 5 2 1 4 8 6 7 3 距离：284

从城市3出发：3 6 1 4 5 2 7 8 3 距离：284

从城市3出发：3 7 2 1 4 5 6 8 3 距离：263

从城市3出发：3 8 1 4 5 2 6 7 3 距离：278

DSO每执行一次所需时间为0.084 885秒，而ACO每次运行的时间大概在0.110 0～0.190 0秒之间。同时，DSO算法在求出从每个城市点出发的最优路径后，算法的自适应部分提供了从该城市点出发的其他可供选择的次优路线解。而ACO算法只能得到从可能城市点出发的最优路线，假如在其求解的最优路线发生其他变化的情况下，其无法提供可供选择的其他次优路线解。因此从以上分析可以得出结论，与ACO算法相比，DSO可以在更短时间内提供更多和稳定的路线选项。

4 结 语

DSO具有用于实现搜索和选择路径的两种模式——走私者(非自适应)和驴(自适应)。在走私者模式下，DSO能够发现所有可能路径和最短路径，而在驴模式下，可利用驴的探索行为来寻找最佳路线以防止第一部分求出的最佳路径不再适应。DSO算法是一种路径协同优化算法，在求解物流车辆配送路线问题上，与ACO算法相比，DSO算法能够在更短时间内提供更多的路径选择和更加稳定的选项。