基于自适应烟花算法和k近邻算法的特征选择算法

黄 欣 莫海淼 赵志刚

1(广西农业职业技术学院信息与机电工程系 广西 南宁 530007)2(合肥工业大学管理学院计算机网络系统研究所 安徽 合肥 230009)3(广西大学计算机与电子信息学院 广西 南宁 530004)

0 引 言

特征选择(Feature Selection，FS)也称为属性选择，它是维数约简中最常用的方法。特征选择是指从原始数据的所有特征中选取特征真子集，并使用该特征真子集来对学习算法的模型进行训练，它不仅能够提高学习算法的学习性能，而且能够有效地对原始数据集进行属性约简，并减少原始数据的冗余信息。

特征选择本质就是一个优化问题，而群智能优化算法则是解决实际工程应用的优化问题的有效工具，这为群智能算法与特征选择相结合提供了一个理论基础[1]，并且吸引了大量学者的关注。张杰慧等[2]将自适应蚁群算法应用于特征选择，然后使用SVM分类器对特征子集进行评价，并且将该特征选择算法应用到计算机辅助孤立肺结节诊断系统，提高了系统的检测和辅助诊断方面的性能。滕旭阳等[3]以信息熵作为评价准则，将粒子群算法和遗传算法各自的优势相融合，并根据特征选择的特点将比特率交叉算法和信息交换策略引入到特征选择算法中，使粒子群和遗传算法种群协同演化，然后一起协作搜索特征子集。陈媛媛等[4]提出了改进蝙蝠算法，将其应用到光谱的相关特征选择，并且可以快速地搜索到全局最优值，能有效地提高波长选择的准确性和稳定性，被选择的波长物理意义明确，采用选择的特征波段建立的定量模型优于用全谱建立的模型。戚孝铭[5]提出了一种基于模拟退火机制的蜂群优化特征选择算法，该特征选择算法在蜂群算法的基础上引入了模拟退火算法的思想，然后对原始数据的特征集进行搜索，使原始数据到达维数约简的目的，并且提高文本分类的效果。路永和等[6]将基本烟花算法进行离散化，然后通过改进烟花算法的相关参数，再将离散化的烟花算法运用到文本分类问题的特征选择中，最终在高维的文本分类问题中得到较好的实验效果。文献[7]将烟花算法和SVM相融合，提出了一种基于融合特征约简(FFR)和烟花算法优化多类支持向量机(MSVM)的混合CCPS识别方法，其中，FFR算法主要由统计特征和形状特征、特征融合和核主成分分析特征维数约简三个子网络组成，从而使搜索到的特征子集对分类结果更加有效，在MSVM分类器算法中，核心函数参数对混合CCPS的识别精度起着非常重要的作用。周丹等[8]提出了一种基于改进量子进化算法的特征选择算法，它是以Fisher比和特征维度来构造新的评价函数，作为评价特征子集优劣的标准，并且能够增加种群的多样性，同时也提高了算法的性能。

1 自适应烟花算法

自适应烟花算法(Adaptive Fireworks Algorithm，AFWA)[9]是根据烟花在夜空中爆炸的自然现象来模拟种群在解空间的寻优过程而提出的一种改进烟花算法。自适应烟花算法的迭代过程和其他群智能算法大同小异，其主要迭代原理为：首先初始化烟花种群；然后计算爆炸强度、爆炸半径、生成爆炸火花种群、生成高斯火花种群；根据“随机-精英”选择策略来选择下一代烟花。通过以上步骤不断地迭代，直到到达终止条件，则算法停止迭代。

2 特征选择

2.1 特征子集产生

特征选择的方法主要分为三种[12]，分别是穷举法、随机方法和启发式。其中，穷举法又分为完备集(完备集包括遍历所有和广度优先)和非完备集(非完备集包括分支定界和最好优先)。但是，虽然采用穷举法来进行特征选择能够保证得到最优的特征子集，但是此方法的时间成本太高，会消耗大量的计算时间，因此在实际工程应用中一般不采取该方法。

随机方法又包括完全概率和概率随机这两种方法。前者是完全按照随机的方式来产生特征子集，这种方法存在很大的不确定性，往往不能够得到最优特征子集；后者是按照一定的概率去选择特征子集。

启发式方法包括向前(向后)选择、决策树、群智能优化算法等。像决策树、向前选择和向后选择这几种方法，能够寻找到在可接受范围内的较优特征子集，但是不一定能够寻找到最优子集；并且在寻找特征子集的过程中，可能在某几个阶段能够较快收敛，但在其他阶段可能收敛得很很慢，甚至会陷入局部最优。而群智能优化算法的方法主要是采取遗传算法、模拟退火算法、粒子群算法和烟花算法等群智能优化算法对数据的特征集进行选择特征子集。由于群智能优化算法具有较强的局部搜索能力，能够在寻优的某个阶段跳出局部最优解，并具有相对较快的收敛速度，在实际工程应用中往往能得到最优特征子集。

2.2 特征子集评价

特征子集的评估方法主要有基于距离的度量方法、基于信息的度量方法、基于依赖性或者相关性的度量方法、基于一致性的度量方法以及基于分类错误率的度量方法。特征子集的评价是通过评价函数来对特征子集进行评分，并以此作为衡量得到的特征子集的优劣。评价函数主要包括过滤式、封装式、嵌入式[12-13]。

过滤式的评价函数是以特征子集的相关度作为评价准则，并通过搜索有序特征子集来直接计算特征子集的距离属性(如欧式距离、chernoff概率距离、马氏距离等)、信息属性(如信息熵、条件熵、信息增益等)、独立属性(如相关性、相似性)、显著检验(t-检验，F-检验，卡方检验)等[18]，最后根据统计检验法来对其特征子集的优劣进行评价。使用该方法对特征子集进行评价，不仅具有较好的泛化能力，而且比较稳健，计算资源消耗小，还可以从一定程度上避免过拟合的情况出现，但是不一定能够得到最优的特征子集。

封装式的评价函数是以学习器(如拟合器、分类器、聚类器)作为黑盒，然后把搜索到的特征子集放到黑盒进行预测，得到的预测效果越好，则说明该特征子集的有用程度越高，反之，则该特征子集的有用程度越低，即通过将搜索到的特征子集对学习器的后期性能的好坏来评价该特征子集的优劣[19]。该评价函数的优点是寻找到的特征子集对后期的学习更有帮助，并且理论上可以寻找到最优特征子集，但是消耗的计算资源较大，并且极易出现过拟合的现象。

在嵌入型特征选择中，特征选择算法是作为学习算法的部分嵌入其中的[20]。嵌入式在原则上能够搜索到最优特征子集，它不仅具备过滤式在寻找特征子集的高效率、不容易出现过拟合现象，并且还具有封装式的高精度。本文采用的是嵌入式的评价函数。

2.3 停止标准

特征子集经过评估之后，需要判断是否满足停止条件，若达到停止条件，特征选择算法停止迭代，否则继续寻找新的特征子集，直到达到停止条件为止。特征选算法的停止条件通常选择以下情况之一或多个组合：

(1) 已经达到设定的特征属性的数目；

(2) 达到特征选择算法的最大评价次数；

(3) 增加或减少特征不能使子集的评价函数值有所提高；

(4) 寻找到了理论最优的特征子集；

(5) 达到了特征选择算法设定的寻优精度。

2.4 结果验证

特征选择算法的结果验证一般是将与特征子集相关的数据进行训练和预测，根据训练和预测的数据与原始的数据集进行比较，然后得到学习器(如分类器、聚类器、拟合器等)的准确度、训练模型的时间成本、预测的时间成本、模型的复杂程度。但是，最重要的是学习器在预测数据时的准确度。

3 特征选择算法设计

3.1 离散化编码

在基于自适应烟花算法的特征选择算法中，个体的位置xi=(xi1,xi2,…,xin)代表一个特征子集。在离散化的自适应烟花算法中，如果xi1等于1，则第1个特征被选中；如果xi1等于0，则表示第1个特征没有被选中。假设xi=(0,1,0,1,1)，表示有5个特征集，0的个数共有2个，1的个数共有3个，则此时该个体选中了第2个特征、第4个特征和第5个特征，而第1个特征和第3个特征没有被选中。由于自适应烟花算法一般解决的是连续性的问题，因此在解决离散化问题时需要将其进行离散化处理。位置xi的离散化处理表示为：

(1)

3.2 适应度函数设计

当选择到的特征子集的特征总数为0时，则无法对数据进行分类。因为特征选择的目的是为了将原始数据进行降维处理，但经过降维处理之后的特征子集的特征总数要大于0，这样的特征子集才使得数据的分类有意义。因此，当出现特征子集的总数为0时，需要对这种情况进行处理。针对这样的约束，需要使用外部惩罚函数对其进行惩罚处理。由于本文讨论的是求解最小化的问题，因此同时将其转化为最小化问题，具体表示为：

(2)

式中：sum(xi)表示个体i选中的特征子集的特征总数；pre表示分类精度。

分类精度pre的计算式表示为：

(3)

式中：TP为正确预测的测试样本数量；FP为错误预测的测试样本数量。

3.3 爆炸算子

爆炸算子主要由爆炸强度、爆炸幅度(即爆炸半径)、位移操作这三个部分组成。其中，爆炸强度是指烟花个体发生爆炸之后所产生爆炸火花的数量，爆炸火花数量越多，则该烟花个体的爆炸强度越大；并且该烟花个体的适应度值越好，则产生爆炸火花的数量越多，反之，产生爆炸火花的数量越少。爆炸强度的更新计算表示为：

(4)

式中：Si是第i个烟花个体所产生的爆炸火花的数量；m是一个用来限制爆炸火花数量的常量；Ymax是适应度值最差的个体；f(xi)是第i个烟花个体的适应度值；ε是一个极小的常数，以避免分母为零。

为了避免爆炸火花数量过大，因此使用下式进行约束：

(5)

式中：round()为四舍五入的取整函数；a和b都是常数变量。

爆炸幅度(即爆炸半径)是指烟花个体发生爆炸之后所发生的位移量。为了计算自适应爆炸半径，需要选择一个个体，其与最优个体，即下一代烟花之间的距离，作为下一次爆炸的半径。选取的个体需要满足两个条件：条件1，适应度值比这一代的烟花要差；条件2，到最优个体的距离，是满足条件1的个体中最短的。条件2表示为：

(6)

式中：si表示烟花生成的所有火花；s*表示所有火花和烟花中适应度值最好的；X表示烟花；d是某一种距离的度量(如无穷范数)。

核心烟花的爆炸半径的计算式表示为：

(7)

非核心烟花的爆炸半径的计算式表示为：

(8)

式中：Ai是第i个烟花个体的爆炸半径；Amax是最大的爆炸半径，Ymin是最优烟花个体的适应度值。由式(8)可知，适应度值越好的烟花个体，产生的爆炸半径越小；反之，产生的爆炸半径越大。

在烟花算法中，随机选择烟花个体的z个维度来进行位移操作，具体的位移操作如下：

(9)

式中：rand(0，Ai)是一个(0，Ai)范围内服从均匀分布的随机函数。

3.4 变异算子

(10)

式中：N(1，1)是服从均值为1、方差为1的高斯分布函数。

3.5 映射规则

在寻优的过程中，需要对越界的烟花个体进行如下的越界处理：

(11)

3.6 选择策略

在自适应烟花算法中，采用“随机-精英”选择策略来选取下一代的烟花，即：从烟花、爆炸火花、高斯火花组成的候选集中选择适应度值最好的个体作为下一代的烟花，下一代的其他烟花则根据候选集的下标进行随机选取。

3.7 k最近邻算法

k最近邻算法(k-Nearest Neighbor，kNN)是机器学习领域中最常用的一种学习算法，它既是一种分类算法，也是一种回归的非参数统计方法，并且被广泛应用于分类问题。kNN算法的操作：首先，对原始数据进行预处理，并将处理好的数据分成训练组和测试组；其次，设置合适的参数k；然后，在训练组中选择初始的最近邻元组；计算初始近邻元组和测试组之间的距离D，并计算训练组和测试组之间的距离L，比较Dmax和L之间的大小，若L大于或者等于Dmax，则停止迭代，否则重复前面的步骤，直到达到终止条件为止。

3.8 十折交叉验证

十折交叉验证是一种用来测试算法准确性的测试方法。它的主要操作是：首先，把数据分成十份，其中九份是训练数据，一份是测试数据，并轮流将训练数据和测试数据进行实验；然后记录每次实验输出的准确率或者错误率，再把十次实验的输出结果的平均值作为对算法准确性的衡量标准。一般需要做N次十折交叉验证的实验，然后再将N次十折交叉的实验结果的平均值作为最终评价算法准确性的标准。

3.9 算法流程

综上所述，本文提出了基于自适应烟花算法和k近邻算法的特征选择算法(Feature Selection algorithm based on Adaptive Fireworks Algorithm and k-Nearest Neighbor algorithm，AFWA- kNN-FS)，该算法的主要流程如算法1所示。

算法1 AFWA- kNN-FS算法流程

输入：烟花种群的位置、经过十折交叉验证法处理之后的数据的全部特征集

输出：烟花种群更新之后的位置、分类精度pre

Step 1 初始化烟花种群；

Step 2 把烟花个体搜索到的特征子集的相关数据放到kNN分类器，然后按式(2)计算该烟花个体的适应度值；

Step 3 根据式(4)计算爆炸强度；

Step 4 根据式(6)和式(7)计算核心烟花的爆炸半径，按式(8)计算非核心烟花的爆炸半径；

Step 5 烟花个体根据式(9)进行位移操作，并产生对应的爆炸火花，然后按式(11)对越界的爆炸火花个体进行越界处理，再按式(1)进行离散化处理；

Step 6 每一个烟花个体根据式(10)产生对应的高斯火花，然后按式(11)对越界的爆炸火花个体进行越界处理，再按式(1)进行离散化处理；

Step 7 采用 “随机-精英”选择策略，从候选集中选取下一代烟花；

Step 8 重复Step 2-Step 7，若达到终止条件，则停止迭代，并输出结果。

4 仿真实验

4.1 选用的UCI数据集

本文的仿真实验采用机器学习常用的UCI数据集来对AFWA- kNN-FS算法的分类性能进行测试，被选取数据集(来源https://archive.ics.uci.edu/ml/datasets.html)如表1所示。

表1 实验选用的UCI数据集

续表1

4.2 实验的参数设置

为了验证AFWA- kNN-FS算法的性能，本文选用了表1的UCI数据集，并且与自适应烟花算法(AFWA)[9]、增强烟花算法(EFWA)[14]、烟花算法(FWA)[15]、蝙蝠算法(BA)[16]、标准粒子群算法(SPSO)[17]进行对比实验，即使用AFWA算法、EFWA算法、FWA算法、BA算法和SPSO算法来进行搜索特征子集，并且将每种算法在搜索过程中搜到的特征子集的相关数据放到kNN分类器进行学习，最终输出相关的分类精度进行比较。其中，五种算法的参数设置如表2所示。

表2 五种算法的相关参数

4.3 实验结果分析

为了更加科学地评价算法的性能，本文将五种算法的种群大小popsize均设置为8，最大评价次数evalsMax均设置为200次(其他的参数设置参照表2)，并且使用“十折交叉验证”的方法做了20次独立重复实验，结果如表3所示。其中，min_acc、max_acc、avg_acc、std_acc分别是20次独立重复实验的最小分类精度、最大分类精度、平均分类精度、标准偏差。表4是五种算法根据平均分类精度这一栏的排名统计出来的结果。

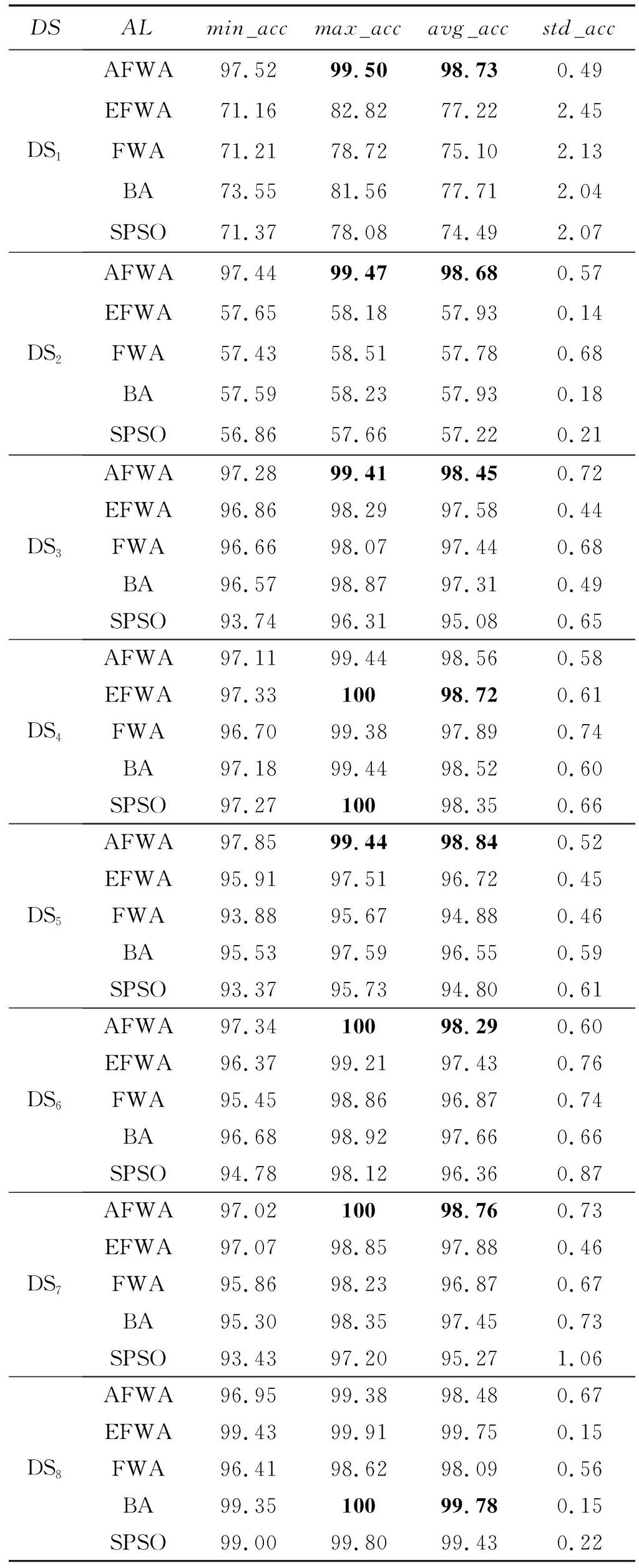
表3 五种算法的实验数据(popsize=8，evalsMax=200)

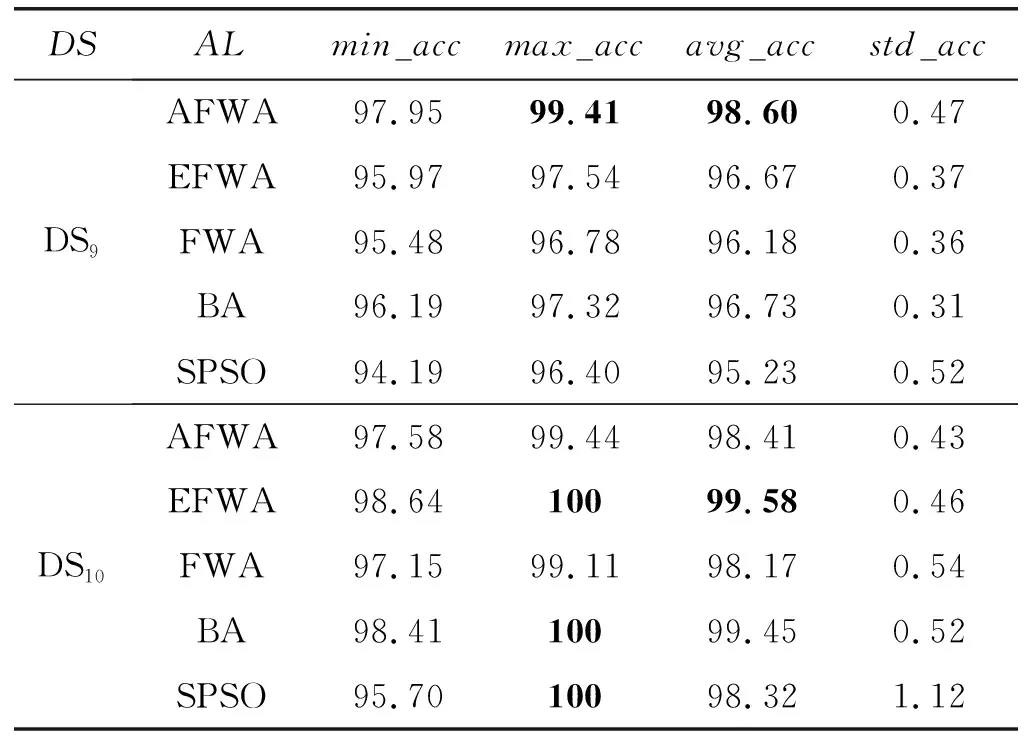
续表3

表4 五种算法在DS1-DS10平均分类精度的排名

由表3可知，根据平均分类精度avg_acc这一栏的数据，对于数据集DS1-DS3、DS5-DS7以及DS9，AFWA- kNN-FS算法的平均分类精度均优于其他四种算法；对于DS4，AFWA- kNN-FS算法的平均分类精度劣于基于EFWA和kNN的特征选择算法，却优于其他三种算法；对于DS8，AFWA- kNN-FS算法的平均分类精度优于基于FWA和kNN的特征选择算法，却劣于其他三种算法；对于DS10，AFWA- kNN-FS算法的平均分类精度劣于基于EFWA和kNN的特征选择算法、基于BA和kNN的特征选择算法，却优于其他两种算法。

根据表3的最大分类精度max_acc这一栏的数据可知：对于DS1-DS3、DS5-DS7以及DS9，AFWA- kNN-FS算法的最大分类精度均优于其他四种算法，并且对DS1和DS2的分类精度(最小分类精度、最大分类精度和平均分类精度)远远优于其他四种算法。尤其在搜索数据集DS2的高维特征时，AFWA- kNN-FS算法的性能远优于其他四种算法。

由表4可知，AFWA- kNN-FS算法的平均分类精度的总体排名优于其他四种算法。因此，在对表1的数据集进行搜索特征子集时，AFWA算法的总体性能优于其他四种算法。

为了进一步验证基于AFWA算法和kNN算法的特征选择算法的有效性，再选用Ionosphere、sonar和wdbc这三个数据集，并且与文献[1]提出的基于自适应粒子群(APSO)的特征选择算法进行对比实验。其中，最大评价次数evalsMax设置为2 000次，AFWA算法的参数设置参照表2，APSO算法的参数设置参照文献[1]。由表5得到的实验结果可知，基于AFWA算法和kNN算法的特征选择算法的总体性能优于基于文献[1]的特征选择算法。

表5 AFWA和APSO的平均分类精度

5 结 语

本文将自适应烟花算法进行离散化处理，使用k近邻算法作为分类器，将特征子集引入目标函数，并使用惩罚因子来处理约束条件，提出了新的特征选择算法，采用十折交叉验证法来检验算法的分类效果。自适应烟花算法具有较好的全局搜索能力，避免在搜索特征子集的过程中过快地陷入局部最优解，并且特别适合于处理高维数据的维数约简问题。仿真实验结果表明，与增强烟花算法、烟花算法、蝙蝠算法、粒子群算法以及自适应粒子群算法相比，本文提出的算法具有相对更好的分类效果。