改进的分水岭T-Snake轮轨接触区域图像分割算法

杨 桐 董 昱

(兰州交通大学自动化与电气工程学院 甘肃 兰州 730000)

0 引 言

安全是铁路运输的重中之重，钢轨对车轮的开放性约束决定了列车脱轨的客观存在性[1-4]。轮轨的接触关系存在正常接触、车轮爬轨和车轮跳轨三种情况，如图1所示。当车轮出现爬轨或者跳轨时，即图中的第二种和第三种接触状态，列车存在着脱轨的可能性，该状态下继续行驶存在着较大的安全问题。也就是说，列车是否脱轨与轮轨的相对位置有关。随着图像检测技术的快速发展，国内外许多学者就脱轨可视化检测装置都是通过图像检测技术来提取出轮轨接触区域踏面(车轮与钢轨顶面的接触部分)边缘曲线，再进一步判断轮轨接触情况。

本文的主要工作就是对车载摄像机获取的轮轨接触图像进行分割处理，提取出踏面的边缘，为下一步过非接触式图像测量技术搭建了高速轮轨接触可视化装置预判列车运行是否可能脱轨奠定基础。文献[5]通过非接触式图像测量技术搭建了高速轮轨接触可视化装置，利用canny边缘检测算子提取出踏面内外边缘线进行拼接得到了最终踏面边缘曲线。但采用两个角度下获取的图像进行拼接，没有进行图像的畸变校正，拼接的结果存在较大的误差[5]。文献[6]提出了基于区域生长的车轮踏面轮廓图像分割算法，该算法的输入图像为无复杂背景的轮缘阴影图像，通过基点位置选取种子点从而确定合适的生长准则，实现了踏面轮廓曲线的提取。但轮轨接触区域道砟、枕木、钢轨和车轮灰度差异较小，该文献的提取未考虑到复杂的背景，实际应用价值较小[6]。文献[7]提出了一种基于改进分水岭算法的彩色踏面图像分割方法，首先基于彩色梯度图像标记了增强后的图像的前景和背景，然后由分水岭变换得到一次分割结果，最后通过图像连通域分割算法完成踏面的提取。利用彩色梯度图进行分割虽保留了细节信息，但算法过于复杂实时性有待提高[7]。

针对上述问题，本文提出了基于改进分水岭的T-Snake图像分割算法。该方法首先通过组合标记后的分水岭变换得到初始踏面边缘，该边缘作为T-Snake模型的目标轮廓。实验结果表明，本文方法去噪性强，可以获得理想的轮轨接触踏面分割结果。

1 基本算法基础

1.1 Snake模型简介

Snake模型为一种主动轮廓线模型[8]，该模型对噪声和对比度不敏感，可以将目标从复杂背景中提取出来并跟踪目标的形变。其思想为：由控制点构成的固定形状曲线，在定义力的作用下使曲线时刻保持连续平滑，并不断地朝着真实的轮廓线逼近。

Snake模型中的目标轮廓线可由能量函数定义，目标函数控制曲线的变形，具有最小能量的闭合曲线就是目标轮廓。其能量函数Etotal定义为：

(1)

式中：第一项为内部能量Eint， 第二项为外部能量Eext。主动轮廓线在内、外力的共同作用下寻求其能量函数的极小值。内部能量Eint表达式为：

(2)

式中：第一项表示弹性能量，数值上等于vt的一阶导数模平方与系数的乘积，其值决定着主动轮廓线的拉伸难易程度；第二项表示弯曲能量为vq的二阶导数模，其数值决定着主动轮廓线的变形难易程度。

外部能量Eext表达式为：

Eext(ν(s))=-k|▽G(v)×▽Ι(v)|

(3)

式中:参数k控制外部能量的大小；I(v)为图像的灰度值；G(v)是高斯核函数；▽为梯度算子[9]。当主动线轮廓接近目标曲线时，该点灰度梯度值增大，Eext(v(s))减小，则该点停止运动。也就是说，利用Snake模型进行图像分割就是求解能量函数Etotal极小值的过程。由欧拉公式可知，式(1)极小化的过程必须满足：

αv″(s)-βv(4)(s)-▽Eext=0

(4)

令v关于t的微分项为：

v(s,t)=αv″(s,t)-βv(4)(s,t)-▽Eext

(5)

当v(s,t)的值达到稳定值时，即可求解出式(5)的值。

1.2 T-Snake模型简介

拓扑自适应蛇模型(topologyadaptivesnake，T-Snake)模型是一种拓扑自适应主动轮廓模型[10-11]。它是对传统的Snake模型进行离散化处理后得到的，一定程度上解决了传统Snake模型对初始目标轮廓选取敏感和弯曲函数对轮廓影响较小的问题。T-Snake模型的思想是将连续曲线看做由n个离散点构成，对于第i个离散点其节点模型如图2所示。

图2 T-Snkae离散点模型

在T-Snake模型中其内部能量函数Eint定义为：

(6)

(7)

由上述公式可得，内外能量函数和的积分即为T-snake模型总能量，求解该能量极小值的过程思想和传统Snake模型相同，也就是求解第i个离散点微分近似项的稳定值。

1.3 分水岭算法简介

分水岭算法是一种源于地理形态学的分割方法，其基本思想是把图像中各点像素灰度值表示成该点的海拔高度，通过高度的不同可将整幅图像划分为若干个区域，每个区域都有其灰度极小值[12-15]。通过模拟注水过程，得到每个聚水盆的水面汇聚脊线为分水岭，也就是待提取的图像边缘线。其理念图如图3所示。

图3 分水岭算法示意图

分水岭算法是一种自适应阈值可调的图像分割算法。在进行阈值选择时，如果阈值R选取得过大，则许多图像的边缘细节提取过程中会存在间断或丢失的问题；如果阈值R选取得过小，提取图像的过程中又会存在着过分割的问题，提取效果不精确。因此，应根据要轮轨接触区域的图像特点选取适当的阈值。针对本文处理的轮轨接触区域原图像，其特点是背景复杂，且背景图像与提取目标灰度差异较小；且由于车辆在行驶过程中存在着车轮与钢轨摩擦而产生损伤边缘的多样性；除此之外，钢轨上存在着连接件如机械绝缘节、鱼尾板、扣件等可能会对踏面分割的效果产生影响。要想获取精确的分割效果要综合考虑以上因素，因此，需要对传统的分水岭算法进行优化。

2 改进图像分割算法设计

2.1 基于组合标记控制的分水岭算法

针对传统分水岭存在的对噪声及其敏感容易产生过分割的问题，本文采用组合标记控制法对分水岭算法进行优化。首先把预处理后的轮轨接触区域图像通过图像信息熵获取梯度图像并标记出像素高峰值，然后用高低帽变换获取最大对比图像并标记出像素低谷值。最后将修正后的图像进行分水岭分割来达到提取踏面边缘曲线的目的。本文采用的改进分水岭分割算法具体结构如图4所示。

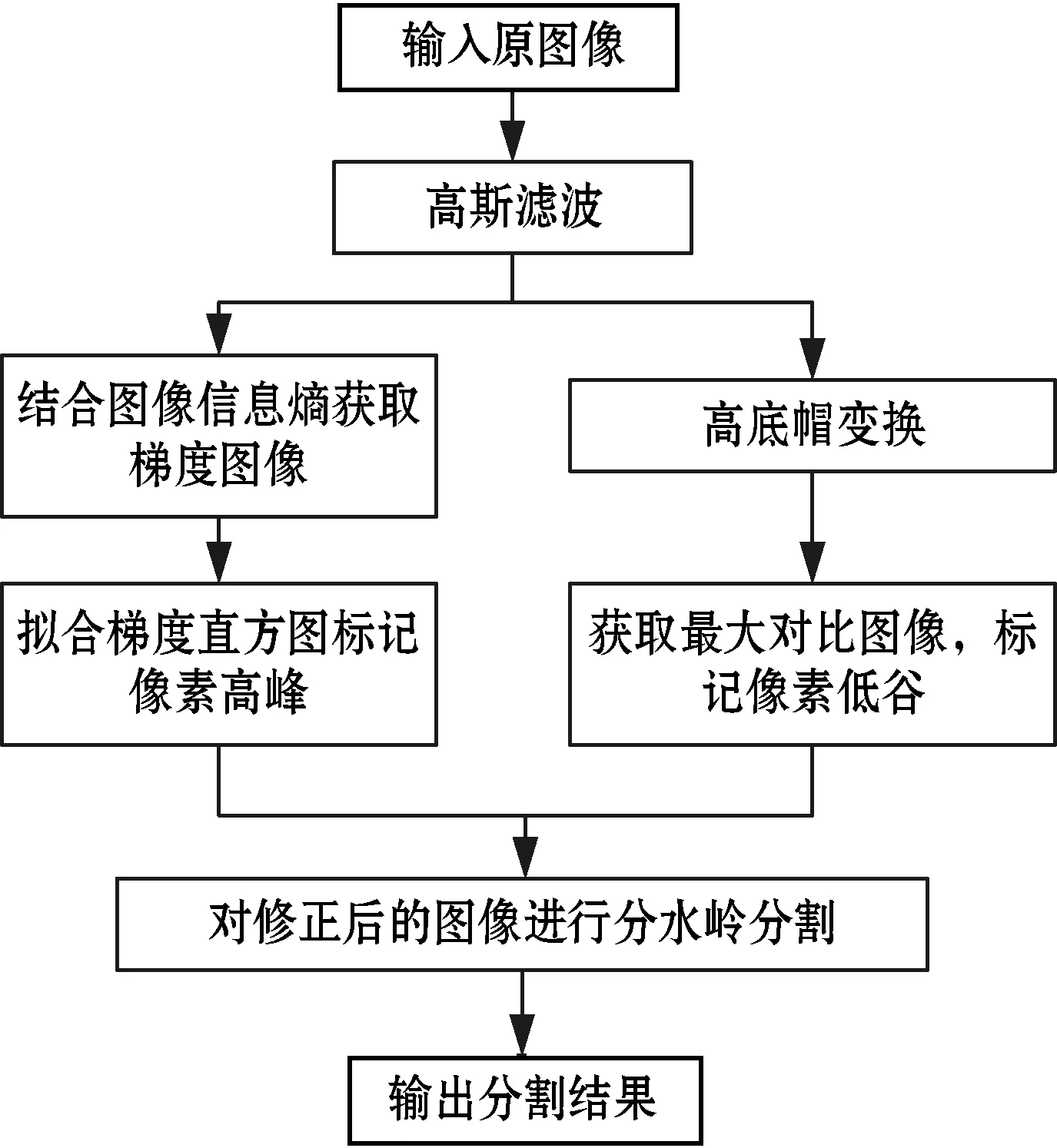
图4 改进的分水岭轮轨接触区域图像分割算法功能流程图

算法步骤如下：

Step 1 对轮轨接触原图像进行高斯滤波处理，得到平滑图像。

Step 2 获取高斯平滑处理后图像的梯度图像，形态学梯度计算数学表达式为：

Grad(I)=δ(I,Dr)-ξ(I,Dr)

(8)

式中：第一项是膨胀操作，第二项是腐蚀操作，Dr为半径为r的圆形结构，I为输入图像。

进行梯度运算后，若选取两个分量梯度极值来合成梯度图像，会丢失边缘细节信息。为了较好地获取边缘细节信息，引入了图像信息熵Hf，其定义如下：

(9)

式中：计算两个分量信息熵，并求出所占比例x和y，从而得到最终梯度图。

(10)

(11)

G=x×Grad(O1)+y×Grad(O2)

(12)

本文采用代码“Out= entropy(Img)”来计算平滑后图像的信息熵。

Step 3 若对Step2中的轮轨接触梯度图像直接进行分水岭分割，仍会出现过分割达不到精确提取的现象，因此需要进行梯度图像的修正来消除局部极小值。由图5(a)可得原轮轨接触图像的梯度直方图H(i)，可以看到H(i)图像的包络线不稳定，波动较频繁。进行平滑拟合后的的直方图如图5(b)所示。

(a) 梯度直方图

(b) 拟合后梯度直方图图5 轮轨接触图像的梯度直方图

通过拟合后的直方图标记出像素的高峰值，数学计算公式如下：

R0={i,H(i)|H(i)≥H(i-1)∪H(i)≥H(i+1)}

(13)

式中:R0是初始波峰值集合。通过去除响铃峰值和小于阈值的峰值得到重构后的梯度图Gc。

通过代码(IndMax=find(diff(sign(diff(data)))<0)+1),对拟合后的梯度直方图标记出高峰值。

Step 4 标记出梯度图像的高峰值后，对平滑后的图像进行高低帽变化，高帽变化可以去除图像中由于光照影响下钢轨和车轮踏面上的极亮细节，从而增强图像的原始的灰度峰值，其数学表达式为：

top-hat(f)=f-(f°c)

(14)

式中:c为结构元素。

低帽变化可以消除由于轮轨接触区域背景复杂灰度差异小而产生的暗细节。经过低帽变化可以标记出图像的灰度谷值，使获取到精准的分割脊线，其数学表达式为：

bot-hat(f)=(f°c)-f

(15)

本文采用的高低帽变化关键代码如下：

It = imtophat(phtx, Se); % 高帽变换

Ib = imbothat(phtx, Se); % 低帽变换

Step 5 将原轮轨接触图像与高帽变化图像相加后再减去低帽变化结果，得到的图像即为最大对比图像，在该图像中标记出像素低谷值。其关键代码如下：

ImageA= imadd(lgyt,It);

ImageB= imsubtract(ImageA,Ib);

IndMax=find(diff(sign(diff(data)))>0)+1

Step 6 使用分水岭算法分割修正后的图像。图6为分割效果，其中:(a)图为轮轨接触原图像，(b)图为高斯滤波后的图像，(c)图为组合标记后的图像，(d)图为最终分割修正后的图像。

(a) 轮轨接触原图像 (b) 高斯滤波后图像

(c) 组合标记原图像 (d) 组合标记分割图像图6 本文分水岭算法分割效果

采用本文的分水岭算法提取的轮轨接触区域的边缘曲线图像，较好地保留了图像细节，改善了原算法的过分割的缺点。

2.2 改进T-Snake模型

T-Snake模型在继承了传统Snake模型优点的同时，还存在曲率约束不足，当图像背景和提取目标灰度差异较小时，分割效果不明显的问题。针对这些问题，本文在式(8)的基础上引入区域能量项ERegion，该区域能量项是基于局部区域的最小方差之上的，将外部能量函数重新定义为：

(16)

式中：η为ERegion的比例值，本文取2。ERegion的定义如下：

(17)

式中:Ip(x,y)为p的灰度值;Ω1为图像内部区域;μ1为灰度均值；相同的Ω2和μ2为外部区域和其灰度均值。式(16)中外力和膨胀力的计算公式如下：

(18)

式中：p和q分别为外力和膨胀力的系数。外力为高斯核函数与输入图像像素值卷积模平方与系数乘积的负数；膨胀力为第i个离散点出单位法向量，二值函数和膨胀力幅度值三者乘积的倒数。当像素值大于阈值时二值函数F(I(x,y))取正，反之取负。通常情况下q为常数，为了提高收敛速度和算法的稳定性，本文将q定义为：

(19)

式中：Ω为离散点i的3×3的邻域；δ为该领域内最大最小灰度值之差;σ和μ为灰度方差以及灰度均值。通常情况下，当边缘轮廓区域灰度均匀时q取1，由于轮轨接触区域灰度差异较小，踏面边缘区域灰度不均匀，q的值处于1～2之间。在膨胀力的驱动下，轮廓离开该区域。

T-Snake模型与传统的Snake模型求解思想相同，都是求解关于轮廓曲线的泛函，当总能量Etotoal最小时，该曲线即为所求目标曲线[16-17]。

3 实验与结果分析

基于以上阐述，为了验证本文提出算法的分割效果，在MATLAB仿真软件中，选用兰州铁路局兰州北编组站提供的轮轨接触图像作为输入图像，采集的图像中线路钢轨材质为U71Mn，其型号为60 kg/m，车轮踏面型号为LM-30，具体实验环境设备参数如表1所示。

表1 实验环境设备参数

实验中相关参数取值如下：参考Snake算法在图像分割方面的应用[18]，式(3)中控制图像外部能量的系数k为5.0，平滑函数中的高斯核函数G(v)为1.35。

式(6)中的弹性系数k1为0.15，弯曲系数k2为0.35，因为本文研究对象轮轨边缘图像具有凹陷部分较明显的特点，所以设定的弯曲系数权重大于弹性系数。基于本文算法验证k2分别为0.20～0.45六组数据可得k2=0.35时Snake算法对凹陷部分捕捉效果最优。具体实验结果图像如图7所示。

(a) k2取0.20 (b) k2取0.25

(c) k2取0.30 (d) k2取0.35

(e) k2取0.40 (f) k2取0.45图7 k2取值对分割结果影响效果对比图

为了客观地评价本文算法的分割结果，引入普拉特品质因数(Pratt’s figure of merit，PFM)和标准误差(Standard Error，SE)这两个评价标准。PFM和SE的计算方法如下：

(20)

(21)

式中:ns为实际实验中提取的像素点个数;nl为理想标准情况下提取出的像素点个数;di为第i个提取点到真实点的距离;c为距离系数本文取5;Ss为实际提取到的边缘特征值;SL为理想情况下的标准边缘特征值。

在轮轨接触输入图像中，手动提取车轮轮缘踏面的边界，将其作为理想标准情况下的目标边界，分别采用传统分水岭算法、标准标记分水岭算法、传统Snake算法和本文算法的实验结果进行对比，并结合算法的迭代次数和收敛时间多角度进行评价，具体统计数据如表2所示。

表2 实验结果评价标准

由式(20)-式(21)可以得出 ，当PFM的值越大且SE的值越小时，提取的踏面边缘越接近于真实边缘。从客观评价标准上来看，本文提出的算法在提取轮轨接触图像中踏面的边缘的实验中PFM与SE系数，以及算法迭代时间与收敛时间上优于其他三种分割方法。由于实际应用中存在着光照曝光、阴天、摄像头抖动等干扰因素，为了验证本文算法的普遍适用性，分别模拟采样了以上情况下的轮轨接触图像进行分割验证。直观可视化的实验结果图像如图8所示，其中：(e)图为曝光加抖动情况，(g)图为阴天情况，(i)图为加入椒盐噪声情况，(f)、(h)和(j)为对应干扰情况下本文算法的分割结果图像。

(a) 传统分水岭 (b) 标记后分水岭

(e) 曝光加抖动 (f) 分割结果

(g) 阴天 (h) 分割结果

(i) 椒盐噪声 (j) 分割结果图8 实验结果对比图像效果图

图8(a)为传统分水岭算法的分割情况，可以看出该方法存在严重的过分割现象，基本达不到提取踏面边缘的效果；图8(b)为图标记后的分水岭算法的分割情况，该方法虽然能对输入的原图像进行有效的分割，但由于部分钢轨和踏面的灰度差异较小并且轮缘存在着磨损的情况，而导致分割结果中将灰度接近的钢轨未进行分割以及磨损部分踏面出现过分割现象，不能结合背景复杂性和实际轮缘存在的磨损情况而进行精确的分割；图8(c)为传统的Snake算法的分割情况，通过手动选取原点由算法确定的插值点共同构成了踏面提取边缘线，但在轮缘曲率过大的地方，可以看到插值点并未逼近真实边缘，分割的效果并不理想；图8(d)为本文算法的分割情况，可以看出本文算法可以较理想地对轮轨接触区域的踏面进行分割。

4 结 语

目前，国内外采用脱轨系数评定车辆脱轨的危险程度来进一步指导防止脱轨的工作。我国铁路采用基于脱轨系数安全标准的车辆性能检测系统，通过测量钢轨受到轮对的作用力计算出脱轨系数来评定车辆脱轨的危险程度。列车是否脱轨由轮轨的相对位置决定，铁路应用IEC 62290-1：2014标准文件中将铁路障碍物检测自动化程度最高等级GOA4定义为设备监控。基于此，本文通过车载机器视觉进行图像分割来判别轮轨接触情况，进一步评定列车行驶的安全性，在工程领域中具有一定的应用前景，也符合未来智能交通的发展趋势。

本文通过高斯滤波进行图像处理，具备较好的去噪能力，能有效地提取轮轨接触区域踏面边缘的图像特征；使用组合标记的分水岭算法获取T-Snake的初始目标轮廓线，有效地解决了主动轮廓线模型依赖初始边缘的问题，优化后的分水岭算法使得图像特征更加明显；通过引入区域面积能量项的模型可改善原算法对弯曲边缘提取能力差的缺点，进而提高分割精度。本文算法虽然在细节处理方面具有优势，但在研究不同型号列车车轮踏面与钢轨的接触关系时，如何做到普遍性和连贯性有待进一步的研究。