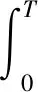一类拟线性波动方程整体强解的存在唯一性
刘兆鹏,李 杰
宿州学院数学与统计学院,安徽宿州,234000
拟线性波动方程是一类非常重要的数学物理方程,在物理学中用来描述具有粘性效应的杆的纵振动。对此类方程的研究,是近年来国内外学者研究的热点[1-5]。1982年,Preste研究了方程
utt-uxx-β(uxt)x=f(x,t)
(*)
的初边值问题。从物理意义上看,该方程与众所周知的方程utt=uxxt+σ(ux)x密切相关,它们都可以解释为具有粘性效应的杆的纵振动。若杆还受到一外力f(x,t)的作用,则杆的振动满足utt-E0uxx-β(uxt)x=f(x,t)[6-8]。
本文将研究比(*)更为广泛的一类拟线性波动方程的初边值问题:
utt-γuxx-β(uxt)x=f(x,t)
(1)
u|t=0=u0(x),ut|t=0=u1(x)
(2)
u(0,t)=u(1,t)=0
(3)
其中,γ为任意常数,此方程是对原模型的推广和补充,从而使其原始模型方程在揭示更为广泛的物理现象过程中得到应用。本文利用Galerkin方法构造方程的近似解,并结合Gronwall不等式得到拟线性波动方程整体解的存在性和唯一性。
1 引理和主要结论

用Galerkin方法构造问题(1)(2)(3)的近似解

其中wj(x)为问题
-wjxx=λjwj,wj(0)=wj(1)=0
的特征函数,则uN(x,t)即αjN(t)满足如下非线性常微分方程的初值问题:
(uNtt,ws)-γ(uNxx,ws)-(β(uNxt)x,ws)=(f,ws)
(4)

(5)

引理1设
(1)β∈C1,β′(s)≥α>0,- 则对任一T>0及(4)(5)的任意解均有估计: ‖uNt‖2+‖uNx‖2+‖uN‖2≤E1, (6) E1,E2及以下诸引理中的Ei(i=3,…,12)均为与N无关的常数。 =2(f,uNt)+2(1-γ)(uNx,uNxt)+2(uN,uNt) -(β(uNxt)x,uNt) =-(β1(uNxt)x,uNt) =(β1(uNxt),uNxt) (7) 2[(f,uNt)+(1-γ)(uNx,uNxt)+(uN,uNt)]≤M1(‖f‖2+‖uNt‖2+‖uNx‖2+‖uN‖2)+α‖uNxt‖2 代入(7)整理,对t积分,由假设ⅱ)及Gronwall不等式可得(6)。 ‖uNxt‖2+‖uNxx‖2≤E3 (8) -(uNtt,uNxxt)+γ(uNxx,uNxxt)+(β(uNxt)x,uNxxt)=-(f,uNxxt) (9) (10) (β(uNxt)x,uNxxt)=(β′(uNxt)uNxxt,uNxxt)≥α‖uNxxt‖2 2(1-γ)(uNxx,uNxxt)-2(f,uNxxt)≤‖f‖2+M2‖uNxx‖2+α‖uNxxt‖2 代入(10),对t积分,由假设及Gronwall不等式可得(8)。 引理3若满足引理2条件,且设 (1)f关于t≥0还是连续的,且f∈L(0,T;L2(Ω)),ft∈L2(0,T;L2(Ω)) 则有估计 (11) ‖uNtt(0)‖2≤(|γ|‖uNxx(0)‖+‖β(uNxt(0))x‖+‖f(0)‖)‖uNtt(0)‖ (12) ‖β(uNxt(0))x‖≤‖β′(uNxt(0))‖‖uNxxt‖≤const 由(12)可得‖uNtt(0)‖≤const。 (13) (β(uNxt)t,uNxtt)=(β′(uNxt)uNxtt,uNxtt)≥α‖uNxtt‖2, 2(ft,uNtt)+2γ(uNxxt,uNtt)≤‖ft‖2+M3+‖uNtt‖2+α‖uNxtt‖2 代入(13),对t积分,由Gronwall不等式可得(11)。 引理4若满足引理3条件,则还有 ‖uNxxt‖2≤E7(0≤t≤T) (14) α‖uNxxt‖2≤(‖uNtt‖+|γ|‖uNxx‖+‖f‖)‖uNxxt‖ 由此引理2,引理3,即得(14)。 推论若满足引理3条件,则有 ‖uNxt‖≤E8(0≤t≤T) 定理1(强解的存在性)设 (1)β∈C1,β′(s)≥α>0,- (2)f∈C0(0,T;L2(Ω)),ft∈L2(0,T;L2(Ω)) (15) 定理2(强解的唯一性) 若β满足定理1条件,则问题(1)(2)(3)的强解是唯一的。 由引理1~4,{uN(x,t)},{uNt(x,t)}于L有界, {uNtt(x,t)}于L(0,T;L2(Ω))∩L2(0,T;(Ω))有界,由列紧性原理,存在u(x,t)及{uN(x,t)}的子序列{uN(x,t)}(子序列仍用原序列表示),使 uN(x,t)→u(x,t)于L(0,T;(Ω)∩H2(Ω)) 弱*收敛 uNt(x,t)→ut(x,t)于L(0,T;(Ω)∩H2(Ω))弱*收敛 uNtt(x,t)→utt(x,t)于L弱*收敛 在(4)两边同乘任一ds(t)∈C0,对s=1,2,…,N1(N1≤N)求和,对t在[0,T]上积分,得 因{uNxt}于H1(QT)有界,故存在子序列{uNxt}使uNxt→uxt于L2(QT)强收敛,且于QT几乎处处收敛,而‖β(uNxt)‖const,ds(t)wsx(x)∈L2(QT)于QT,应用Lebesgue逐项积分定理,可得 故(15)成立,从而u(x,t)即为问题(1)(2)(3)的如本定理所述的整体强解,即存在性得证。 定理2的证明设u,v为问题(1)(2)(3)的两个强解,令w=u-v,则w满足 wtt-γwxx=β(uxt)x-β(vxt)x 两边同乘wt作内积,分部积分,并利用中值定理,可得: 0<θ<1。由上式可得: 对t积分,由w满足初始条件及Gronwall不等式,可得w≡0。即唯一性得证。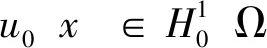

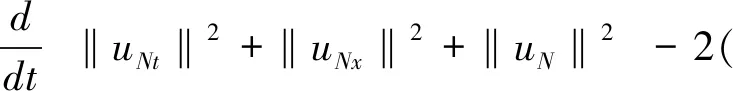

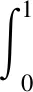


证 将(4)两边同乘,对s求和得

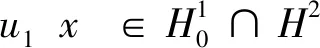
证 将(4)两边同乘,对s求和,令t=0可得:


证 由(9)可得


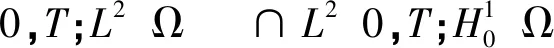

2 定理的证明