p-进位域上可定义群的一个注记
韩 筱,陈国龙
1.淮北师范大学数学科学学院,安徽淮北,235000; 2.宿州学院,安徽宿州,234000
p-进位域是关于p-进位绝对值的完备化,记作p,其包含了所有有理数,是它的一个稠密子域,在许多方面的性质都类似实数集R。 在有关p-进位域(或p-进位闭域)以及实域(实闭域、o-极小结构)的问题研究中,可定义群的分类和描述,强调可定义性而不是可解释性。文献[1-3]对p中可定义群进行了研究,但未对一般的p进闭域进行深入分析。可定义群具有实p进李群的一般特性[4],并且局部同构于实p进代数群,这一结果在文献[1]中得到了进一步的推广。
本文使用基本的模型论理论,参考文献[1,2,5-10]中关于p-进位域(p,+,×,0,1)的模型论方法,讨论了p-进数域p上的可定义群G,G局部同构于p上连通代数群H的p-进点群H(p),证明了当G维数为1时,H为代数几何维为1的连通代数群,p-进位域中一维可定义群是有限可交换的。
1 预备知识
定义1无限结构被称为几何结构[1],若
(1)在Th(M)的任意模型N中,代数闭包算子定义了一个准几何,即满足交换定理:若a,b∈N,A⊂N且b∈acl(A,a)acl(A),则a∈acl(A,b)。
(2)对于M语言中任意公式φ(x,y),都有n<ω,使得在M中任意b,φ(x,b)M是有限的,当且仅当|φ(x,b)M|sh≤n。
定义2设M为饱和的几何结构,具有下列诸性质:
M具有性质(E):若X⊂Mn是可定义的且dim(X)=m,则X上没有可定义的维数为m的等价关系E。
M具有性质(S1):若X⊂Mn是可定义的,dim(X)=m且φ(x,y)为公式,则对于i<ω不存在bi,使得对于所有i,dim(X∩φ(x,bi))=m,但对于i≠j,dim(φ(x,bi)∩φ(x,bj)) (3)任意几何结构都具有性质(E)或(S1):若一些等价的、全部的饱和模型Th(M)具有这个性质。 定义3若有限指数群G的可定义子群族FG的基数 引理1设M为几何结构[1]。 (1)若A⊂B⊂M,且Φ(x)是A上的一个局部型,则dimA(Φ)=dimB(Φ)。 (2)令φ(x,y)长度(x)=n,假设mn,则存在公式ψ(y)使得对于任意b,dim(φ(x,b))=m当且仅当ψ(b)(这个等价关系在任何模型中都成立)。 (3)令X1,X2,…Xk为Mn中的可定义子集,则以下式子成立,dim(X1∪X2∪…∪Xk)=max{dim(Xi):i=1,2,…,k}。 引理2令F为R或p,A为F的可数子集,X为Fn上的可定义子集,则X包含A上一般点,即存在a∈X,使得dim(a/A)=dim(X)。 引理3G为域p上的可定义群,且G有p-进李群的可定义结构。 若G为可定义群且维数为k,则它为p-进李群的维数也为k。 注1 在引理3中可令f为可定义开子群G到H(p)的同胚映射,因为任何(可定义)p-进李群都有一个(可定义)紧开子群,而紧p-进李群是无限的。 引理4G为域p上的可定义群,由引理3给出的群G及其拓扑。 若H为p上的一个连通代数群,H的代数几何维数等于G的维数,且f为G中单位元的开领域U与H(p)单位元的开领域V之间的同胚映射,则当a,b∈U且ab∈U时,f(ab)=f(a)f(b)。 定理1M为一个几何结构,X是维数为K的可定义集X⊆Mn,且f为X到Mn上的一个可定义函数。 若对于所有的b∈Im(f)都有维数为k的f-1(b),则Im(f)是有限的。 证明设M是饱和的,且定义了X和f上的参数。 假设Im(f)是无限的,取b∈Im(f),使得dim(b)≥1。 当dim(f-1(b))=k时,取a∈f-1(b),使得dim(a/b)=k。由次可加性得dim(a,b)>k。 当b∈dcl(a)时,dim(a)>k,这与a∈X,dim(X)=k矛盾则可知Im(f)是有限的。 定理2M为一个几何结构,G是M中的可定义群G⊆Mn且dim(G)=k。 假设G0存在(在饱和模型上考虑),G包含维数为k的可定义子集X,则对于任意的a,b∈X,ab=ba,G为可交换的有限群,即G有一个有限指数子群H,使得H是可交换的。 证明对任意a∈X,设f为G到G上(可定义)函数,fa(g)=gag-1a-1。 结论1固定a∈X。 对于任意g1,g2∈G,fa(g1)=fa(g2)当且仅当g1CG(a)=g2CG(a)。 结论2对于a∈X,Im(fa)是有限的。 证明G的中心化子a,记为CG(a),由假设可知G包含X,CG(a)的维数为k。 所以对于任意g∈G,dim(gCG(a))=k。 由结论1可知,对于所有g∈G,fa是gCG(a)上的常量。 再由定理1可得结论。 结论3对于任意a∈G,CG(a)在G中有有限指数。 证明由结论1可知Im(f)是G/CG(a)上的双射,又由结论2可得CG(a)在G中有有限指数。 在饱和模型M中,由紧致性定理得,对于任意a∈G,CG(a)在G中有有限指数。 假设存在G0,CG(X)=∩a∈XCG(a)是有限次交,则G的有限指数子群H也是如此。 对任意a∈H,CG(a)包含X,则它的维数也是k。 由结论1,2,3可知,对于a在H而不在X中,则由以上证明可知,对于所有a∈H,CG(a)在G中都有有限指数,即H∩CG(H)在G中有有限指数且是可交换的。 注2 对于定理1和定理2,在实元组的型上只需要有有限值次加性维数,对于定理2只需要有维数为k的可定义集X⊂G,使得对于所有的a∈X,CG(a)维数为k。 定理3G为域p上的可定义群,H为p上的一个连通代数群(同引理3),则下面两条件是成立的。 (1)若H是可交换的,则G是有限可交换的。 (2)若G是在p维数为1的群,则G是有限可交换的。 证明(1)令U,V分别为G和H(p)单位元的开领域,且f为U与V之间的同胚映射(同引理4),假设a,b∈U1,ab=ba,取G中包含单位元的较小的开领域U1,使得任意的a,b∈U1,ab∈U。U1的维数和G维数一致,与p作为几何结构的维数相同,则G0存在(在饱和模型上),即G是可交换无限的。 (2)若G的维数为1,由引理3可得连通代数群H的作为代数群的维数也为1,即H是可交换的。 本文主要结果的证明是从局部交换到有限交换,然后再把它放到几何结构中。 利用p-进位域(p,+,×,0,1)的模型论方法,证明了当G是局部可交换的,等价于p上连通代数群H(p),使得可定义群G局部同构于H(p)且是可交换的,从而得到G是有限可交换的。 特别地,当G维数为1时,则H为代数几何维数为1的连通代数群,从而导出p-进位中一维可定义群是有限可交换的。2 主要结论
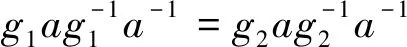
3 结 语

