Fisher-Tippet分布拟合的超声图像联合双边滤波方法

李蒙蒙，邵良志，崔文超，孙水发

三峡大学 计算机与信息学院，湖北 宜昌443002

1 引言

超声成像因其无创、无放射性损害、快捷方便等特性，广泛应用于医学临床诊断。然而，超声图像中固有的乘性散斑噪声，在图像表面形成的颗粒状现象，严重影响了对成像组织的准确判读，限制了超声图像自动诊断技术的发展[1]。因此，有效消除散斑噪声对提高图像视觉质量，呈现精确细节信息具有重要作用[2]。

传统的双边滤波（Bilateral Filter，BF）方法[3]由于其有效的边缘保持平滑能力，是目前最常见的加性噪声去噪滤波器之一。但BF 方法固有不足是利用噪声图像计算权值，在强噪声背景下会造成计算权值较大的偏差[4]。Petschnigg 等人[5]提出的联合双边滤波（Joint Bilateral Filter，JBF）方法，其通过导向图像计算权值，能够更好地保留图像细节，同时降低噪声。姒绍辉等人[2]在BF方法基础上，借助分数阶微分梯度算子增强高频以及平滑区域纹理细节。这些改进方法能有效去除加性噪声，但不适用乘性散斑去噪。为此，Balocco等人[6]提出了散斑消减双边滤波（Speckle Reduction Bi‐lateral Filtering，SRBF）方法。该方法局部加权系数不仅考虑了像素间的空间距离，也考虑了分布相似性，能较好地消减超声图像散斑同时保留边缘细节。然而，由于BF 方法的固有不足以及Rayleigh 分布拟合存在的较大偏差，致使SRBF 方法辨析图像均匀区域内噪声信息不够准确，一定程度上影响散斑消减性能。

对乘性散斑去噪处理，同态滤波也一直是研究的热点之一。其基本思想是通过对数变换，将乘性散斑噪声转换为加性噪声，然后进行加性高斯噪声滤波，最后作反对数变换来获得去噪结果。张海锋等人[7]针对单一同态滤波和中值滤波去噪时易损失重要细节的缺陷，提出两者相融合的散斑噪声图像恢复算法。最近，Deled‐alle 等人[8]将块匹配与三维滤波（Block-Matching and 3D filtering，BM3D）方法和双域图像去噪（Dual Do‐main Image Denoising，DDID）方法以同态方式用于散斑去噪，取得较高的信噪比，且图像细节保留较好，然而BM3D和DDID计算复杂度较高[9-10]。

本文针对前述SRBF 方法存在的问题，作出了两个方面的改进，一是用JBF 框架代替BF 框架，即以导向图像计算权值，有效减小权值计算偏差；二是通过散斑包络信号满足Rayleigh 分布，导出散斑图像信号应满足Fisher-Tippet（FT）分布，并将分布相似性利用FT 分布拟合进行计算，有效提高散斑拟合的计算精度。实验结果对比的定量分析证实本文提出的两方面改进都能有效提高散斑消减性能。

2 相关方法

2.1 BF方法

如图1所示，Nr(x)表示待处理像素x的r×r 大小的邻域，对该邻域内每一个像素值f(x+t)，t ∈Nr(x)，BF方法采用局部加权平均实现去噪处理，其表达式为[3]：

式中，ct为空间邻近度因子，定义像素x+t 与待处理像素x的距离权：

其中，||t||表示像素x+t 与像素x 的欧氏距离，σc表示距离权的标准差。

幅度相似度因子st定义像素值f(x+t)与待处理像素值f(x)之间的幅度相似权：

图1 局部邻域关系示意图

其中，σs表示幅度相似权的标准差。

由式（3）可知幅度相似权利用噪声图像计算像素值间的差异，在强噪声背景下可能导致过大或过小的计算偏差[4]，影响BF方法的去噪性能。

2.2 JBF方法

对BF 方法存在的固有不足，JBF 方法基于无噪的导向图像计算幅度相似权[5]，其表达式为：

对比式（1），JBF方法采用导向图像g 计算幅度相似度因子sgt如下：

其中，σgs表示导向图像幅度相似权标准差。

在图像去噪任务中，导向图像通常包含真实图像的某些相似结构信息，这些先验知识的引入能有效提高去噪性能，然而对某些具体的应用，导向图像无法获得。常用的替代方案是采用中间滤波结果作为导向图像[10]，本文提出的算法采用该方案。

2.3 SRBF方法

SRBF 方法将式（1）中的幅度相似度因子st替换为分布相似度因子pt，其表达式为：

其中，分布相似度因子pt定义为：

其中，RLx+t(y)是对像素(x+t)的局部邻域Nr(x+t)（如图1所示）作Rayleigh分布拟合所得的概率密度函数表示拟合分布RLx+t(y)的方差，其最大似然估计为[6]：

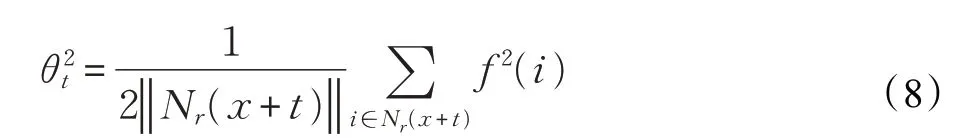
其中，||Nr(x+t)||为局部邻域Nr(x+t)的像素总数。

由式（7）可知，分布相似度因子pt定义为待处理像素f(x)属于分布RLx+t(y)的概率。对比BF方法仅利用像素点间的幅度信息来度量幅度相似性，SRBF 利用局部邻域的整体幅度信息作分布拟合，一定程度上减小了噪声敏感性，然而其仍然采用噪声图像进行计算，无法避免类似BF 方法的固有不足。另外，Rayleigh 分布通常拟合散斑包络信号[6，11]，而适配显示设备的超声图像往往压缩包络幅值，从而使图像中散斑噪声满足非Ray‐leigh分布[11]。

3 Fisher-Tippet分布拟合的联合双边滤波方法

针对前述SRBF 方法利用噪声图像计算权值易产生偏差问题，采用JBF 框架进行有效改进，即用导向图像计算相关权值，且导向图像采用去噪中间结果；对超声图像的散斑统计分布，从满足Rayleigh 分布的包络信号出发，导出散斑图像满足FT 分布，并以FT 分布计算分布相似权。以下对提出的FT 分布的散斑消减联合双边滤波方法（Speckle Reduction Joint Bilateral Filtering based on Fisher-Tippet distribution，SRJBF_FT）如何改进散斑统计分布拟合及JBF框架的改造进行具体阐述。

3.1 散斑统计分布拟合改进

一般地，超声成像系统采集到的超声包络信号Y 满足Rayleigh分布：

式中，σ 为Rayleigh分布噪声的标准差。

包络信号Y 幅度值通常具有较高的动态范围，为适配超声成像系统的显示设备，需要对包络信号Y 进行对数压缩处理，形成散斑图像信号Z：

其中，Z ∈[0,+∞)，可推导其满足FT分布[11]：

因此，式（6）的分布相似度因子pt相应修改为：

其中，FT分布参数ηt在邻域Nr(x+t)中可由最大似然估计得到[11]：

为进一步说明散斑统计分布拟合的有效性，选取如图2（a）所示的真实颈动脉图像进行实验，图像大小为538×340，白框标示了选取的局部均匀区域，分别使用Rayleigh 分布和FT 分布进行局部区域直方图拟合，如图2（b）所示。可观察到，FT分布拟合效果优于Rayleigh分布。

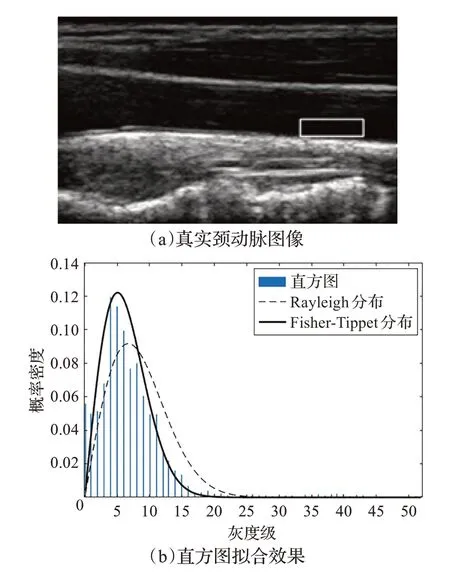
图2 局部均匀区域的Rayleigh分布和Fisher-Tippet分布直方图拟合效果对比

3.2 JBF框架改造

针对SRBF的BF框架存在的问题，本文从JBF框架作相应改造，得到迭代滤波表达式为：

其中，gt表示从导向图像计算的分布相似度因子，即

其中，FT分布参数ηt估计为：

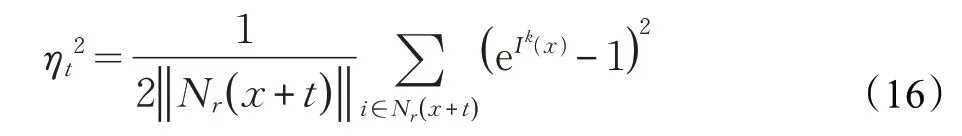
式（14）中k 为迭代次数，k=0时导向图像为原始噪声图像，即I0( x)=f(x，)k ＞0时前一次滤波结果Ik( x )作为当前滤波的导向图像，当前后两次滤波结果的均方差小于给定的阈值时，迭代结束。

4 实验结果及分析

以Matlab R2018a 为仿真平台，选用合成超声图像和真实超声图像，对其他5 种方法（同态BF、同态JBF、SRBF、同态BM3D、同态DDID）与本文方法SRJBF_FT的去噪效果进行了测试对比。另外，仅对SRBF 方法作JBF框架改造，而保留原始Rayleigh分布拟合的方法（以下称为SRJBF）也进行了实验对比，以验证本文对SRBF两方面的改进都能有效提高散斑消减性能。

4.1 合成超声图像实验

图3（a）为标准无噪肾脏图像，大小为256×256。两种模拟散斑噪声的方法生成超声图像，一是按文献[12]方法，对复数域的高斯随机场进行低通滤波处理，取其幅值作为散斑噪声，仿真得合成图m，如图3（b）所示；二是采用Matlab 的imnoise 函数对图3（a）进行散斑加噪，噪声方差取0.02，仿真得合成图n，如图3（c）所示。

图3 合成超声图像实验用图

以图3（b）和图3（c）作原始图像，本文方法实验参数r=7，k=2，空间邻近度因子ct的重要参数σc分别取1.6 和1.4，图4（b）～（h）和图5（b）～（h）分别是7 种方法的实验结果。

为量化7 种方法去噪结果与标准无噪图像的差异，选用均方误差（Mean Square Error，MSE），特征相似度（Feature Similarity，FSIM），品质因数（Pratt's Figure of Merit，FoM）作为衡量指标。

式中，M，N 分别为I 的长度与宽度。

特征相似度能够量化两幅图像在特征上的差异，其定义为[14]：

其中，Ω 表示整个图像空间域，SL表示测量相位一致性（Phase Consistency，PC）和梯度幅度（Gradient Magni‐tude，GM）特征的相似性，PCm是所有PC 特性中最大的PC 特性。

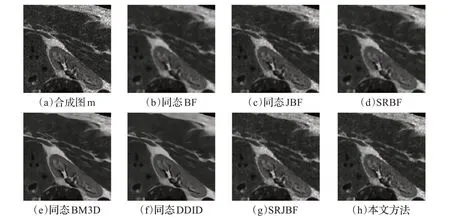
图4 合成图m去噪结果对比

图5 合成图n去噪结果对比

品质因数能够客观地比较去噪后图像的边缘检测质量，表达式为[15]：

式中，NI和NÎ分别为理想的和实际检测到的边缘像素个数，α为常数（通常取α=1/9），di表示第i 个边缘像素点到最近理想边缘像素点的距离。

以上三种指标中，MSE 越小，去噪性能越好；FSIM和FoM值越大，去噪性能越好。

表1列出了7种方法对两幅合成超声图像的去噪结果对比，可看出不论合成图m还是合成图n，单方面改进的SRJBF 方法具有比SRBF 更好的性能指标，表明本文方法中JBF 框架改造有效提高了去噪效果。另外，本文两方面改进的SRJBF_FT 方法相比SRJBF 方法进一步提升了散斑消减性能，具有最优的客观评价，表明FT 分布的散斑拟合改进也能有效提高算法性能。

4.2 真实超声图像实验

在真实超声图像去噪任务中，选用乳腺肿瘤图像和颈动脉图像进行实验，图像大小分别为356×284和384×399。由于真实图像的评价指标须基于图像中均匀区域计算[16]，因此，为客观评估7 种去噪方法，白框标示了选取的局部均匀区域，如图6（a）和图7（a）所示，本文方法实验参数分别取r=9，k=4，σc=2。图6（b）～（h）和图7（b）～（h）显示了本文方法与对比方法的实验结果。

表1 几种方法与本文方法对合成超声图像的去噪性能比较

图6 乳腺肿瘤图像散斑去噪效果对比

图7 颈动脉图像散斑去噪效果对比

表2 几种方法与本文方法对真实超声图像的去噪性能比较

选用固有信噪比（Inherent Signal to Noise Ratio，ISNR）、散斑抑制指数（Speckle Suppression Index，SSI）、散斑抑制和均值保存指数（Speckle Suppression and Mean Preservation Index，SMPI）进行去噪效果评估，令μx和σx分别表示原始图像均值和标准差，μy和σy分别表示去噪图像均值和标准差。

其中，固有信噪比能够量化去噪图像的噪声减少程度，其定义为[16]：

散斑抑制指数能够通过原始图像的散斑指数对去噪图像散斑指数进行归一化，其定义为[11]：

SSI 的取值范围为[0，1]，其值越小，散斑去噪性能越好。然而若去噪算法高估了去噪图像的均值，则SSI可能无法正确评估去噪效果，为避免这种影响，选用散斑抑制和均值保存指数作去噪质量评价，其定义为[16]：

表2列出了7种方法对两幅真实超声图像的去噪结果对比，可以看出处理乳腺肿瘤超声图像时，对SRBF单方面改进的SRJBF 方法和两方面改进的本文方法对去噪效果提升不够明显，且两项指标都低于同态DDID方法，但本文方法获得最优的SMPI 指标。对颈动脉图像，同态滤波方法表现不佳。单方面改进的SRJBF 对SRBF 性能有较小的提升，而两方面改进的本文方法获得显著的散斑消减性能。再次表明本文所提出的两个方面的改进都能有效提高算法的散斑消减性能。

4.3 参数讨论

为衡量参数设置对本文SRJBF_FT 方法的影响，选取4.1 节的合成图，MSE 为衡量指标进行实验。图8～10显示了不同参数与去噪性能的曲线关系。对于邻域半径r，两条曲线均在r=7达到谷值，随着r 增大，MSE 值缓慢增大，性能变差；另外邻域半径越大算法计算量越大，因此合适的邻域半径取值范围为[5，11]。对于迭代次数k，图9 能明显观察到两幅图像实验结果均在k=2获得最优的去噪性能，表明本文方法具有较快的迭代收敛特性。对于距离权标准偏差σc，可以看到两幅合成图的最佳取值分别为1.6 和1.4，根据性能曲线建议该参数的取值范围为[1，2]。

图8 r 对本文方法去噪结果的影响

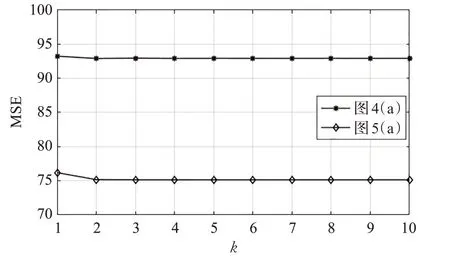
图9 k对本文方法去噪结果的影响

图10 σc对本文方法去噪结果的影响

5 结束语

提出了Fisher-Tippet 分布拟合的联合双边滤波方法。该方法将新的分布相似度因子耦合到联合双边滤波框架，有效改进SRBF 方法两方面的不足，实现了对超声图像较好去噪的同时有效保留其边缘细节特征。下一步的研究方向将考虑通过合理的分布函数模型，拓展提出的方法应用到其他医学成像模式的去噪任务。