局部感受野的宽度学习算法及其应用

李国强，徐立庄

燕山大学 电气工程学院，河北 秦皇岛066004

1 引言

随着互联网技术的蓬勃发展，如何对有效数据进行准确且快速地提取成为人们关注的问题。神经网络的快速发展为数据处理提供了便利条件[1-2]，早期的神经网络工作主要集中于解决调整参数和网络层次结构问题，特别是梯度下降参数的求解，但都存在着固有的缺陷，如：学习收敛速度慢，易于陷入局部极小等问题。目前，神经网络在语音识别、图像处理、物体识别等众多领域得到广泛应用[3-4]，并且取得了很大的成功，其中较为流行的神经网络模型为反向传播（Back Propagation，BP）网络[5]，以及在图像处理方面取得较大突破的深度学习（Deep Learning，DL）[6]，例如：卷积神经网络（Convolu‐tional Neural Networks，CNN）[7-8]、深度置信网络（Deep Belief Networks，DBN）[9]、深 度 玻 尔 兹 曼 机（Deep Boltz-mann Machine，DBM）[10]。但是，DL 网络为多层神经网络结构，样本量较多且网络结构复杂，因而存在训练速度较慢的问题。而网络结构较为简单的BP 网络，也存在迭代求解速度较慢且易陷入局部极小解的问题。

宽度学习系统（Broad Learning System，BLS）[11]的提出为以上问题提供了一种解决方案，该模型作为深度学习的替代方法被提出。BLS 的优点在于它利用动态更新算法[12]对新添加的节点进行快速处理而不需要重新建立模型。在原有模型的基础上进行优化处理，不仅让添加新节点的模型变得更加精确，同样地，也极大地节省了模型重构所需要的时间。但是面对图像分类时，要想达到高准确度的要求，依然需要上万个隐藏节点来对网络进行建模，普通的硬件配置很难正常运行。基于局部感受野的极端学习机（Local Receptive Field based Extreme Learning Machine，ELM-LRF）[13]是 将CNN 和极端学习机（ELM）[14]进行结合，根据神经元在神经网络中拥有局部感知的特点，提出加入局部感受野的思想（LRF），使得该模型对图像的识别拥有更高的准确率和更好的稳定性。因此，本文将ELM-LRF 中局部感受野的部分提取出来与BLS结合，构建了基于局部感受野的宽度学习网（BLS-LRF），该模型分别从局部和全局两方面对图像特征进行快速提取。并且保留了BLS动态更新节点的特点。实验采用MNIST 数据集和NORB 数据集对该网络进行测试，并且将测试结果和传统的神经网络进行对比，实验结果表明BLS-LRF 网络只需要很少的节点就能达到传统网络的测试精度，同时，训练和测试的时间也大幅度的缩短。

2 宽度学习算法

许多神经网络都被耗时的训练所困扰，主要的原因是由于层级之间含有大量的参数，导致训练周期增长。其次，如果已经建立的模型没有达到期望的目的，那么它将消耗大量的时间再次进行重新训练，宽度学习网的设计为以上问题提供了一种有效的解决方法。宽度学习系统是由澳门大学陈俊龙教授提出的一种新型学习算法，其结构如图1所示。

图1 宽度学习网

BLS 的设计思想来源于随机向量函数链式神经网络（Random Vector Functional-Link Neural Network，RVFLNN）[15]，结构如图2 所示，RVFLNN 通过对网络结构的扩展，将多层网络转换为单层网络，使该网络具有极强的非线性映射能力，达到了快速、高效的学习目的，避免了陷于局部最小的问题，尽管RVFLNN 有着显著的速度和不错的性能，但伴随着大数据时代的到来，面对不断更新的数据RVFLNN 模型的重构能力又有明显的不足。为了适应更多的数据量，BLS网络结构应运而生。它在RVFLNN 的基础上添加了由原始输入到特征节点层的算法，将所提取到的特征值作为输入层连接到增强节点层。并且BLS 网络中还添加了动态逐步更新算法[12]，在不需要重新训练模型的前提下对新添加的数据或隐层节点进行快速处理，即在原有模型的基础上对新的节点或数据进行优化处理，让新模型拥有更好的泛化性能，同时也极大地节省了模型重构所需要的时间，第三部分对动态更新算法进行了详细的解释。BLS 不但完美继承了RVFLNN 的优点，而且还能快速高效地处理数据，从而节省许多的时间。目前，很多神经网络也是以BLS为基础进行改进的，例如宽度学习系统的通用逼近能力（Universal Approximation Capability of Broad Learning System，UAC-BLS）[16]，模糊宽度学习系统（Fuzzy Broad Learning System，FBLS）[17]。

图2 随机向量函数链式网络

根据图1 的网络结构来对BLS 进行描述，首先，原始输入层通过稀疏编码算法得到了数据的映射特征。其次，映射特征作为特征节点层通过激活函数连接到增强节点层，其中的权值随机产生。最后，所有的特征节点和增强节点作为输入直接连接到输出，为了找到所需的连接权值，采用最小二乘法[18]的改进算法岭回归[19]求得隐藏层与输出层之间的输出权值。具体过程如下：

其中，Wik表示第i组映射特征中的第k 个特征节点与所有输入的连接权重，Wei∈RM×k表示第i 组的特征映射与所有输入的连接权重。β代表着偏置。

图3 基于局部感受野的极端学习机

因此，特征节点层中所有的特征映射可以被记为：

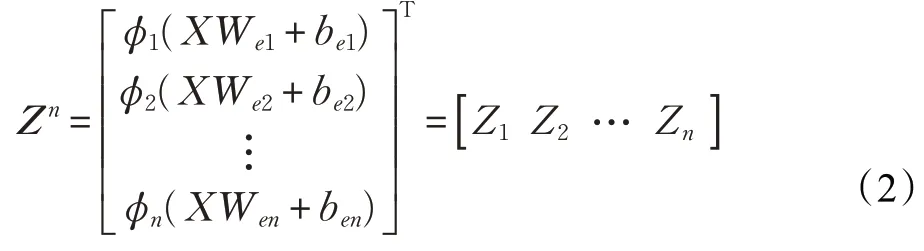
同理，第j组的增强节点通过特征节点可求得：

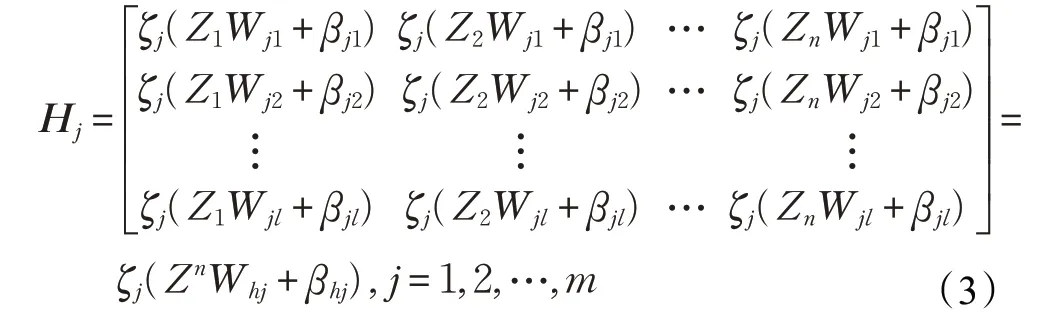
其中，Whj∈Rkn×l和βhj是随机权重和偏置，ζ(⋅)表示激活函数，l 表示第j 组增强节点的数量。然后，前m 组的增强节点可被记为：

最后得出网络输出与网络的关系如下：

3 基于局部感受野的宽度学习网

基于局部感受野的极端学习（ELM-LRF）是由南洋理工大学的黄广斌教授提出的，网络结构如图3 所示。该网络模型主要由三部分构成：

（1）利用局部感受野的特性对图像进行局部特征提取。为了获得充分的局部特征，可以设置K 组不同输入权重，每组输入权重形成一个特征映射图，最终获得K个不同的特征映射图。

（2）卷积操作和平方根池化的过程。假设输入层大小为d×d，局部感受野大小为r×r，可得出特征映射图的大小是( d- r+1)×( d- r+1)，池化图和特征图大小相同。

（3）利用正则化最小二乘法求解输入权重的过程。由图可知池化层与输出层是全连接的，将池化层中所有组合节点的值构成一个行向量，假设有N 个输入样本的行向量，最终得到的组合矩阵为，利用最小二乘法得到最终的输出权重W。

从网络结构及原理来看，ELM-LRF 网络融合了CNN 的思想。它们都是直接处理原始输入，利用局部连接的方法限制网络模型的学习。但不同的是ELMLRF 可以根据不同的概率分布来进行随机的采样，而CNN只能使用卷积隐藏节点来采样。并且CNN训练完成后还需要误差反向传播算法（BP）[5]来进行调整，需要耗费大量的时间，而ELM-LRF 网络只需要随机地生成输入权重而不需要后期的调整。使得该模型相比于CNN可以节省大量的时间。

提出的BLS-LRF 网络结构是将BLS 和ELM-LRF中的LRF 思想相结合，ELM-LRF 可以由连续概率分布随机生成不同形式的局部感受野作为输入数据，而BLS则是采用对图像进行全局特征提取的方法来对模型训练。将两个网络模型进行结合，可以从局部和全局两方面对图像特征进行提取，达到增强网络测试精度的目的。模块结构如图4所示。

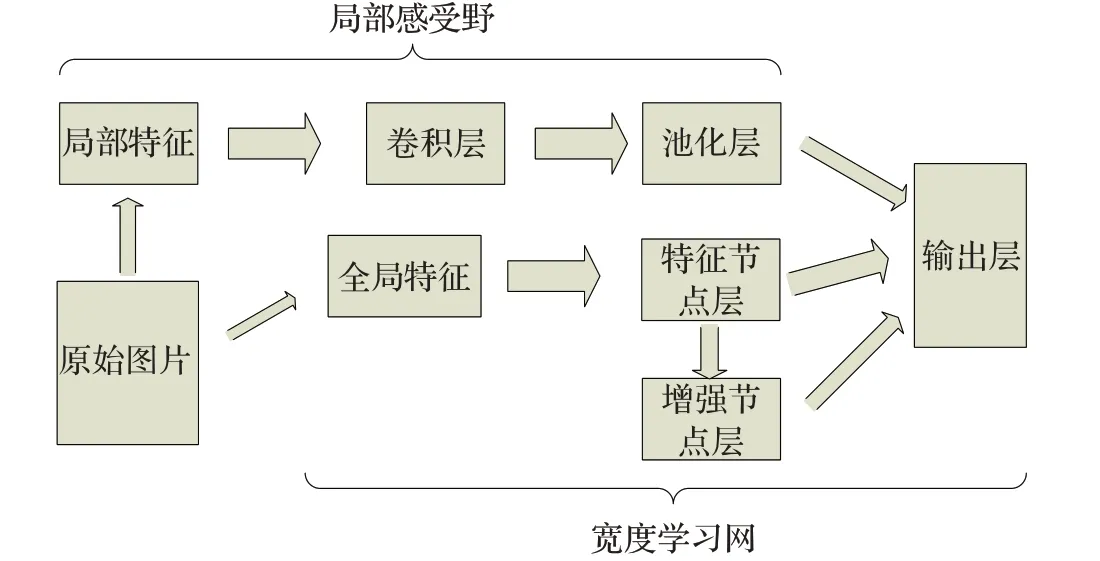
图4 BLS-LRF网络模块图

表1 NORB数据集测试精度对比

根据结构可以看出不改变BLS算法的基础上，只需将ELM-LRF 中的局部感受野部分与BLS 合并，即池化层的输出与BLS最后的隐层（包括特征节点层和增强节点层）作为输入层与输出层进行连接。在宽度学习网的基础上拓展出最后隐层的输出，记为A=[Zn|Hm|D]其中D是ELM-LRF池化层的所有输出矩阵。

对于输出层权值采用伪逆的方法求取，根据公式：

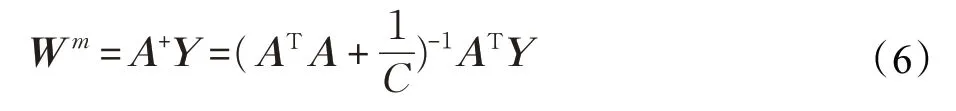
求得输出层的权值Wm，其中Y 表示期望输出是约束权重的系数。

澳门大学陈俊龙教授等人提出了一种动态逐步更新算法（增量学习），该算法对新添加节点相关的权重立即更新，这项工作为以后需要增加节点的网络铺平了道路，同时它为经典模型的权值更新提供了一种有效快捷的方法。BLS 的增量学习算法便是在此基础上被设计出来，它可以通过动态增加节点（特征节点和增强节点）来达到提高精度的目的，而BLS-LRF 网络结构不但能从多方面提取输入特征，而且还保留了BLS动态更新节点的优点即增量学习算法。动态增加增强节点的具体过程如下：

假设网络初始结构有n 组映射节点和m 组增强节点，网络的最后隐层的输出记为Am=[Zn|Hm|D]。当增加p个增强节点时，特征节点和新增加的增强节点之间的 关 系 为 Hm+1=[ζm+1(ZnWhm+1+βhm+1)]，其 中Whm+1∈Rnk×p，βhm+1∈Rp，得 到 新 的 最 后 隐 层 记 为Am+1=[Am|Hm+1]，根据增量学习算法[11-12]可以得出新矩阵Am+1的伪逆。

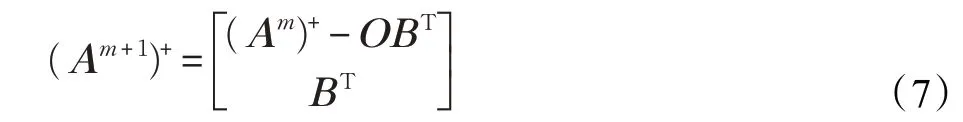
其中O=(Am)+ζm+1(ZnWhm+1+βhm+1)

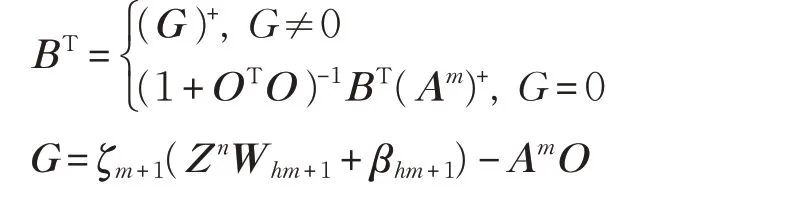
因此，新的权重是：

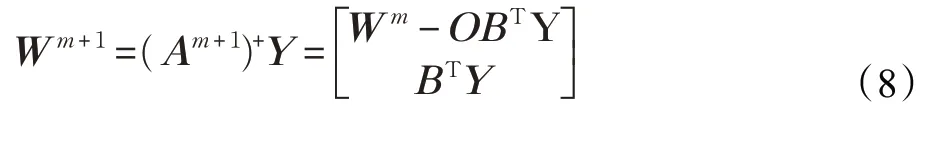
4 实验结果与分析

为了证明BLS-LRF 的有效性，对两个经典数据集MNIST和NORB进行测试，然后将BLS-LRF分别与BLS和ELM-LRF测试结果进行对比。参考文献[11]选取BLS网络最优的节点和最佳参数C。参考文献[13]且经过多次测试得出C等于0.01 时为ELM-LRF 最佳参数。本次测试是在Windows 7（64 位）、Inter i7-7820X、3.60 GHz CPU和32 GB RAM的台式机Matlab环境下运行的。

4.1 NORB数据集

NORB 数据集一共有48 600 张图像，该数据集主要应用于对3D 玩具模型识别的实验[20]，其中包含50 个玩具分成5 个不同种类：四肢动物、人像、飞机、卡车和汽车。在各种照明条件下，选取不同的方位角和高度对取样物体进行成像，最终形成了48 600张图像。选取其中的24 300 张图片作为训练集，其中包含25 个玩具（每种类型5 个）。将剩余的24 300 张图片作为测试集，同样包含25个玩具（每种类型5个）。

根据文献[11]可知，BLS 网络选取100×10 的特征节点和9 000个增强节点是对NORB数据集测试精度最优的节点设置。ELM-LRF 参数设置为4×4 的感知域、10个特征映射图和池化大小为3。BLS-LRF 参数设置为10×10 的特征节点、900 个增强节点、4×4 的感知域、3 个特征映射图和池化大小为3。测试结果如表1所示，3个网络结构进行对比可以看出，BLS-LRF 的测试精度是最高的，并且训练和测试的总时间是最短的。而BLS网络的测试精度虽然和BLS-LRF 的差不多，但是训练和测试所花费的总时间却是BLS-LRF 的两倍。为了更好地体现BLS-LRF 的有效性，采用现在主流算法和该网络进行对比，其中包括两种栈式自编码算法SAE 和SDA[21]、深度置信（DBN）、多层感知算法（MLP）[22]、深度玻尔兹曼机（DBM）、多结构极端学习机（MLELM）[23]及多感知极端学习机（HELM）[24]，以上算法的实验均在Intel-i7 2.4 GHz CPU，16 GB RAM Matlab 环境下运行，实验的分类结果引用于文献[24]。实验结果如表2所示，从测试精度来看，尽管本文提出的方法精确度90.08%不是最好的，仅次于HELM 的91.28%。从训练时间来看，本文提出的方法所用时间是18.46 s，是所有算法里所用时间最短的。因此综合来看，BLS-LRF算法对NORB数据集分类是有效且快速的。

表2 NORB数据集分类结果

BLS-LRF算法不仅对以上无增量学习算法有效，面对增量学习算法同样有效。为了证明BLS-LRF 网络在增量学习中的有效性，将BLS 的增量学习算法和BLSLRF的增量学习算法进行比较，这里只讨论动态增加增强节点。首先BLS 的初始结构为100×10 的特征节点和2 000个增强节点，对增强节点更新5次，每次增加1 000个增强节点，结果如表3 所示。BLS-LRF 的初始结构为4×4 的感知域、3 个特征映射图、池化大小为3、10×10 的特征节点和200个增强节点，同样对增强节点更新5次，但每次增加100个增强节点，结果如表4所示。经过表3和表4 的对比可以得出，BLS-LRF 不但每次动态更新的精度高于BLS，并且每次动态更新所需要的时间相比于BLS缩短了3～5倍，由此可以看出BLS-LRF对于增量学习算法也具有一定的促进作用。

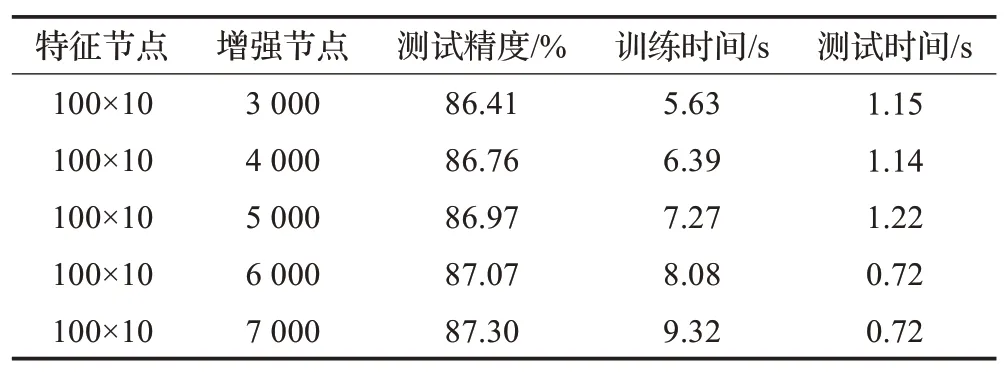
表3 BLS对NORB数据集的增量学习算法

表4 BLS-LRF对NORB数据集的增量学习算法

4.2 MNIST数据集

MNIST 数据集作为经典的手写数据集被广泛应用[25]。这个数据集包含了70 000 张手写数字图片，其中有60 000张图片作为训练样本，剩余10 000张作为测试样本。每张图像是一个单一的手写数字图片。对于BLS 网络结构参考文献[11]，选取最优节点数即10×10的特征节点和11 000的增强节点。对于ELM-LRF设置5×5 的感知域、30 个特征映射图和池化大小为3 去进行测试。为了证明BLS-LRF网络的快速性，设置了5×5的感知域、3个特征映射图、池化大小为3、10×10的特征节点和5 000 个增强节点去和上面两个网络进行对比，对比结果如表5所示，可以看出前3组的测试精度相近，但是所需要的时间长短却不相同，BLS-LRF的测试时间是最短的为35.2 s，其次是BLS 的51.71 s，最后是ELMLRF 的84.8 s。因此BLS-LRF 的网络模型要优于BLS和ELM-LRF。

表5 MNIST数据集的测试精度对比

其次，将BLS-LRF 中的3 个特征映射图增加到10个特征映射图就得到了BLS-LRF对MNIST数据集最高的测试精度99.06%，训练时间为112.73 s，总时间为124.85 s。同样引用文献[24]中的测试结果，得到了表6，另外为了突出BLS-LRF 的优越性，添加了目前比较流行的深度学习网络与其进行对比。这里采用CNN 和残差神经网络（Resnet）[26]来对MNIST数据集测试，之后将测试结果与BLS-LRF 做比较。对于CNN 设置5 层结构（2 个卷积层、2 个池化层和1 个全连接层）卷积核为5×5、池化大小为2、输出通道为6 和12，数据每批次为50，一共迭代20 次。测试环境与BLS-LRF 的测试环境相同。对于残差网络采用56 层结构（55 个卷积层和一个全连接层），其中卷积层分成4 个模块，第一个模块只包含一层卷积，其余的3 个模块分别包含18 个卷积层，每个模块的输出通道分别为16、16、32、64。所有卷积的卷积核大小为3×3，数据每批次为128，一共迭代了1 000次。测试平台是在Nvidia TITAN Xp GPU（12 GB），编程环境为Python3.6，使用的深度学习框架为Tensor‐Flow，测试结果如表6所示。

表6 MNIST数据集分类结果

可以看出Resnet 的测试精度是最高的99.31%，但是它所要求的配置却是GPU，而BLS-LRF 只需要普通配置便可完成实验。BLS-LRF 的测试精度仅次于HELM 和Resnet，并且和DBM、MLELM 的测试精度相近，但是从时间角度来看，BLS-LRF 的训练时间要明显小于它们4 个网络的训练时间。而BLS-LRF 的训练时间不是最短的，仅高于BLS 网络，但是对于BLS 网络来说98.74%是它所能达到的最高精度，而BLS-LRF 的最高精度99.06%是明显高于BLS 的。因此综上所述，本文提出的算法对于MNIST 数据集的分类是高效且快速的。

5 结论

本文提出了一种改进的BLS 网络结构，在BLS 的基础上结合了ELM-LRF 网络形成了BLS-LRF，该网络可以分别对图像进行局部特征提取和全局特征提取，从而对图片分类有了较高的精确度，并且训练速度有了很大程度的提高，为BLS在未来的应用中提供了一种新的方法和途径。该网络也保留了BLS 增量学习的优点，对增量学习中的动态增加增强节点进行了讨论，发现在精度相近的情况下，每次更新的时间缩短了3～5 倍。因此，本文所提出的网络结构对于图片分类是快速且高效的。