受控双向远程量子控制

彭家寅

内江师范学院 数学与信息科学学院，四川 内江641199

1 引言

量子物理学的核心原理之一是量子纠缠，它似乎可以瞬间传输信息，但实际上并不违反经典光速，因为没有通过空间的“运动”。量子纠缠被视为量子信息处理和量子计算的一种有用的资源，如量子隐形传输[1]、超密编码[2]、量子对话[3]、量子秘密共享[4-8]、量子态制备[9-12]、量子信息集中[13-14]等。Briegel 和Raussendorf 提出了一种被称为簇态的新的纠缠态，这种纠缠态可以在任何具有伊辛型相互作用的系统中有效地产生[15]。该簇态可用作隐形传态[16-17]、量子信息集中[14]、密集编码[17]等。

1993年，Bennett等人[1]首次发明了量子态隐形传态（QST），在其传输中，任意未知状态可以在不发送任何物理粒子的情况下被传输到空间遥远的地方，但需借助于先前共享的纠缠和局部操作以及经典通信。此后，QST 在理论和实验上都引起了人们的广泛关注[2-12]，它在包括双向控制隐形传态（BCQT）在内的许多量子任务中都得到了有效的应用。Zha 等[18]于2013 年提出双向控制量子隐形传态，该方案以5 个粒子簇态为量子信道，参与者Alice 和Bob 可以在监控者Charlie 的控制下同时交换他们的未知量子态。不久，Shukla[19]、Chen[20]、Duan[21]和Zhang[22]独立提出了一系列确定性BCQT 协议。Shukla 等[19]讨论了BCQT 方案在量子远程控制和量子密码学方面的一些潜在应用。作为BCQT 的推广，Peng等[23]提出了一种双向量子态共享协议。

2001年，Huelga等[24]首先提出了量子算子隐形传输（QOT）的概念，它可以看作是一个量子遥控器。他们进一步分析了如果去除了一般的要求会发生结果，并描述了可以远程执行酉算子集，而不需借助双向QST[25]。在上述初始工作基础上，一些基于资源消耗和算子限制的其他QOT 协议[26-30]不断被提出来。例如Dur 等[26]利用线性光学元件探索了非确定性量子逻辑算子的隐形传输；Wang[27-28]将处理单粒子算子的原始QOT 协议拓展到涉及多粒子的QOT 协议；Zhao 和Wang[29]提出了一种基于双向QST[25]和Wang[27-28]协议的混合协议，他们[30]进一步提出了一种块对角形式的非局域算子的局域与远程执行协议等。

本文提出了受控双向酉算子隐形传输（CBROT）的概念，它实质上是双向控制量子态隐形传态和量子算子隐形传输的一种有序融合。本协议的目的是：在监管者Charlie和David的控制下，发送者Alice想对含有Bob的粒子之任意量子态上远程地执行一个酉算子U，同时，Bob 也打算对含有爱丽丝的粒子的另一个任意状态上执行另一个酉算子V，整个过程不依赖于双向QST。首先，提出了一种关于任意酉算子传输的方案，然后改进这个方案，接着讨论对算子集加以制的方案。可以发现：酉算子集合越受限制，所节省的经典资源和量子资源就更多。

2 受控双向酉算子隐形传输

假设有空间分离的四个合法用户：Alice、Bob、Char‐lie 和David。Alice 是单粒子算子U 的初始执行者，Bob是另一个单粒子算子V 的初始执行者，Alice 和Bob 互为他们的代理商，Charlie 和David 是两个控制者。此外，在监察者Charlie 和David 的控制下，Alice 可能不了解算子U，但她想在远程的Bob 拥有的一个粒子态上成功地执行U；同时，Bob 也可能不了解算子V，可他打算在Alice的量子态上实现V，这里x,y,α和β 都是复数，并且满足归一化条件和，而U 和V 是任意酉算子。连接四个用户的是两个五粒子团簇态：

和

其中下标表述不同的粒子。事先，这些粒子被假定安全地分配四个合法使用者：Alice拥有四粒子组(A,A′,a,a′)，Bob 拥有四粒子组(B,B′,a,a′)，Charlie 有单粒子C，David有单粒子D。该方案被设计为如下五步：

步骤1 Alice和Bob进行Bell态测量

（1）Alice用Bell基

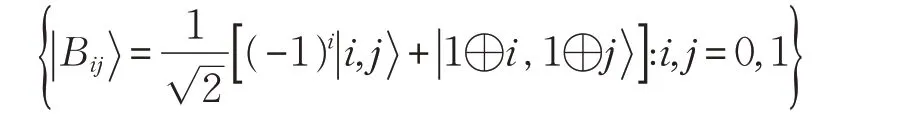
上述测量后，粒子b,a′和D的态塌陷为：

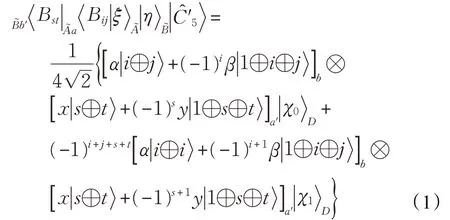
其中，i,j,s,t ∈{0,1}，并且

为单粒子基。

步骤2 Alice和Bob进行酉算子运算

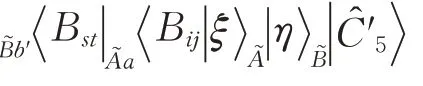
步骤3 Alice和Bob进行第二次测量

（1）Alice 对她的粒子对(A,a′)进行Bell 态测量，同时，Bob也对他的粒子(B′,b)施行Bell态测量。

（2）Alice 和Bob 分别将测量结果(m,n)和(k,l)发送给对方。即，Alice 利用经典信道Alice-Bob 将2 bit 信息(m,n)告知Bob，同时，Bob 用经典信道Bob-Alice 把2 bit信息(k,l)告知Alice。当然，事先约定：信息(m,n)和(k,l)

其中，i,j,k,l,m,n,s,t ∈{0,1}，符号σ(e,f)为Pauli算子。

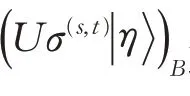
步骤4 Charlie和David进行单粒子测量

（1）Charlie用单粒子基

对粒子C 进行投影测量，同时，David用同样的基对粒子D进行投影测量。

（2）Charlie 和David 通过经典信道将两个1 bit 信息h和r 告知Alice和Bob。自然，两个1 bit信息h和r 分别对应单粒子态和

步骤5 通过合作重构原始酉算子

如果Charlie和David愿意提供帮助，且Alice和Bob彼此也同意合作，那么他们分别能够作用在粒子A′的态上的算子V 和B 粒子的态上的算子U。否则，Alice和Bob都不能单独完成量子任务。

注1 从远程态制备[11]和QOS[31]的研究来看，如果放宽协议必须适用于任意算子这个一般性条件，那么CBROC任务就可以完成。下面，展示了这一点。

注意等式（1）在Alice 和Bob 的交换下是对称的，因此只考虑Alice对U 是部分了解的，故她必能得到不难看出，发生这种情况的条件是U 满足：

其中，W 是对应于任何U 而言，从某些限制集S 中提取的一个有效的通用算子；θ 是一个实参数，它对应同一集合中不同的U 可能会不同，有：

显然，如果U 与σ(k,l)是交换或反交换的，则这样的W 可能是存在的。如果Uσ(k,l)=σ(k,l)U 对于k,l ∈{0,1}成立，则：

如果Uσ(k,l)=-σ(k,l)U 对于k,l ∈{0,1}成立，则：

因U2非酉算子，故它不是希望的。尽管U1是最简单的酉算子，但若把它用于上述方案的话，本方案就失去量子控制作用。这表明如果选取限制集S={U1}于上述方案的话，那将是没有意义的。

3 改进的CBRQC协议

仍考虑第2章的量子任务，并设计如下的方案。

步骤1 Alice和Bob进行受控非门操作

其中，u为控制粒子，v为目标量子。

步骤2 David、Alice和Bob进行单粒子测量

根据国外技术可知，栽培基质温度达80℃时，可消灭大多数病原菌、害虫。病菌和害虫的杀灭温度[4]，如图1所示。无土栽培基质蒸汽消毒机的栽培基质蒸汽加热温度可达120～200℃，通过灭菌检测均达到99.9%以上，消毒效果非常明显。

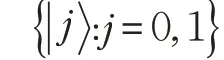
其中，i,j,l ∈{ }

0,1。

步骤3 Alice和Bob执行酉运算

（1）Alice 和Bob 根据收到的信息分别对他们的粒子对(a,a′)和(b,b′)施行酉运算和，于是变成：

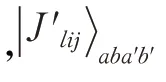
步骤4 Alice和Bob进行Bell态测量

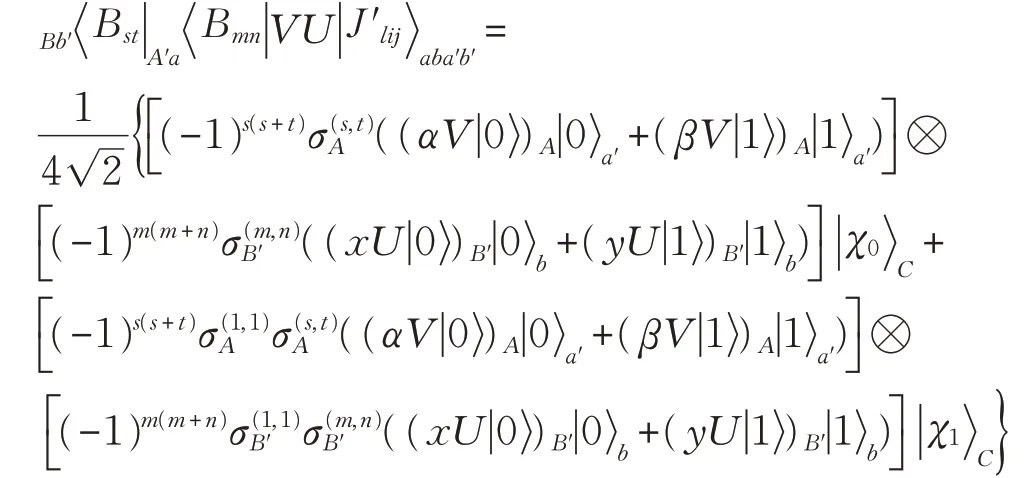
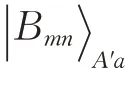
步骤5 Charlie进行单粒子测量

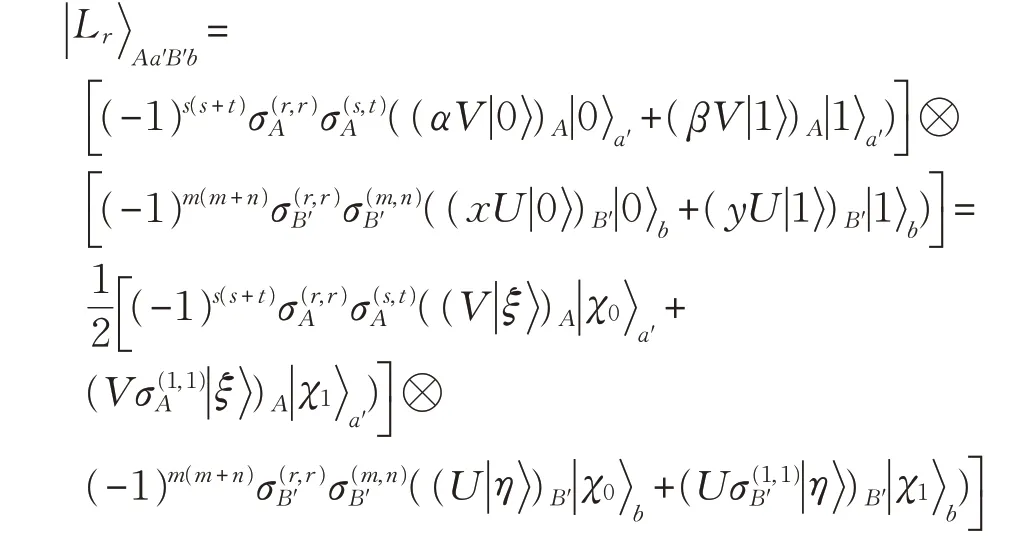
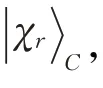
步骤6 Alice和Bob重构量子态

类似注1 的讨论，期望Alice 对U 有部分的了解，那么她就能确实地获得显然，可类似地推出下列等式：

显而易见，当U 与σ(k,l)是交换或反交换的时候，这样的W 是存在的。如果Uσ(1,1)=σ(1,1)U，则：

这里θ和ϕ是两个任意实参数。如果Uσ(1,1)=-σ(1,1)U，则

其中，a和b是实参数，使得a2+b2=1 并且ia+b=eiϕ。U1对应于关于z 轴的任意一个旋转，U2为在x-y 平面上围绕任意轴的π旋转。利用这个协议，限制集S={ }U1,U2中的算子都能被Alice在Bob的粒子B所在的态上确切地执行。这个结论可以应用到Bob 部分了解算子V的情形，也就是当V 取S中的任一算子时，它也能被Bob在Alice 的粒子A′所处的态上执行。因此，Alice 和Bob的算子U和V 都取自S={U1, U2} 时，它们分别在和态上被成功地施行，因此本方案能完美地将两个特殊但粒子算子完美地双向传输。

注2（1）比较本章与上章的方案，改进的协议的概率提高了一倍，它使一些特殊的算子能够通过双向完美地传输，但它需要更多的局域操作。

（2）如果直接修改第2 章中描述的方案，可以得到与改进方案相同的结果。事实上，仅需添加操作于等式（1），剩余过程作相应修改就可。

4 资源与限制算子博弈的双向受控协议

在第3 章中，提出了 基 于算子 族S={U1, U2} 的CBRQC协议，其中U1和U2分别是式（2）和式（3）所示的酉算子。本章将看到：如果把酉算子U 和V 限制到S中，那么就可以设计一个更简单的CBRQC协议，从而进一步节省资源。不失一般性，假设U=U1且V=U2，其中：

开始前，Alice、Bob 和Charlie 分享第1 章中所示的五粒子团簇态，具体地，Alice 拥有粒子对(A,A′)，Bob 拥 有 粒 子 对(B,B′)，而 粒 子C 属 于 监 控 者Charlie。注意Alice 和Bob 的粒子A͂和B͂分别处于未知态和按照这些要求，协议可以设计如下。

首先，Alice和Bob的操作如下：

（1）Alice 和Bob 分别对各自粒子对(A,A′)和(B,B′)施行两粒子运算NAA′和NBB′，于是联合态变成：

（3）根据上述测量结果，Alice对粒子A和A′分别施行Pauli运算σ(0,s)和σ(0,t)，对应地，Bob对粒子B和B′执行Pauli运算σ(0,s)和σ(0,t)。这样变成：

（4）Alice 和Bob 分别对粒子A′和B施行U1和U2运算，则

其次，Alice、Bob和Charlie需做如下操作：

经过上述测量后，粒子A和B′的态坍塌为：

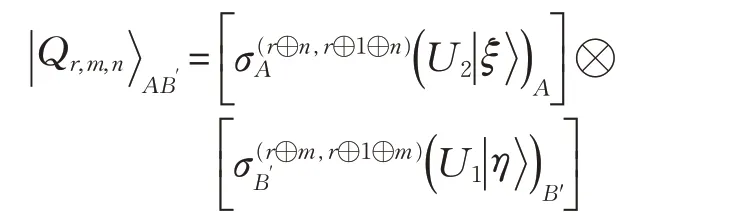
它正是所需要的。因此，借助五粒子团簇态和经典通信，Alice 和Bob 分别对应算子U1和U2能分别在和上被成功地执行。

注3（1）到目前为此，已经讨论了有序算子对(U1,U2)被双向执行，这里U1和U2分别来自等式（2）和（3）。对于有序算子(U1,U1)、(U2,U1)和(U2,U2)的讨论是类似的。

（2）本方案仅用了一个五粒子团簇态作为信道，来自控制者的单向经典信息是1 bit，Alice 和Bob 都需要2 bit经典信息。而在第2章和第3章的每个方案中都需要两个五粒子团簇态、来自控制者的2 bit 单向经典信息，并且Alice 和Bob 都至少需要经典信息。当然，本章方案的代价是U 和V 的取法必须限制在U1或U2上。

5 讨论与结论

从以下四个方面来比较本方案：由经典部分和量子部分组成的资源消耗、必要的操作复杂性（包括难度和强度）、方案成功概率和方案的内在效率。比较本方案的四个方面结果总结在表1 中。任何单量子算子共享方案的内在效率为：

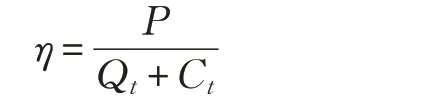
其中，Qt为量子信道的量子位数目，Ct为被传输的经典比特数目，P 协议成功的概率。在表1 中，QRC 表示这些方案包含量子资源耗费，NO 表示必要运算，CRC 表示经典资源耗费，C5表示五粒子团簇态，BM 表示Bell态测量，SM 表示单粒子测量，CNOT 表示受控非门，PO表示Pauli算子，S及其带上下标表示方案。

对于双向任何单量子算子的传输，第一个方案本质上是三个过程的有序结合，即BCQST 和Alice 和Bob 的算子之执行以及重构这三个过程的有序结合。第一个方案中的量子操作复杂性明显简化。注意，一般来说，Bell 态测量的复杂性可以分解为一个CNOT 和两个单量子测量。因此，第一个方案的难度大约等于两个CNOT、两个Bell 态测量和六个单量子测量以及四个Pauli 操作。与表中的第二行相比，从第一行可以看出所有这些优势。显然，第一个方案比第二个方案（S2）少四个Pauli 操作。但第一个方案的成功概率和内在效率都比第二个方案（S2）小得多。当然，如果通过添加适当的局部幺正运算来修改第一个方案，可以得到与第二个方案（S2）相同的结果。此外，方案S2不能简单地分解为上述三个过程，这一重要的变化将带来上述的一些差异。尽管它看起来更复杂，但实际上它提供了资源消耗的上限，并显示了完成CBRQC任务所需操作的复杂性。具体来说，在方案中，两个五粒子团簇态和10 bit的经典通信耗费是必不可少的，必要的操作是两个受控非门、两个Bell 态测量和六个单量子测量，以及八个Pauli 操作，其内在效率为1/20。

表1 四个方案S1、S2、和S3的比较

表1 四个方案S1、S2、和S3的比较

S U 或VQRCNOCRC/bitP η S1任意2C54BM，2SM，4PO101/41/80 S2任意2C52CNOT，2BM，6SM，8PO101/21/40 S#2U1或U22C52CNOT，2BM，6SM，8PO1011/20 S3U1或U2C52CNOT，5SM，6PO511/10

方案的安全性完全取决于四方或三方是否事先安全地分享了量子纠缠信道。借助于类似任务的成熟检查策略[32-33]，任何恶意的局外、局内攻击都很容易被发现（为了简单起见，这里不再重复），这意味着目前的方案也是绝对安全的。另外，本方案是受控的，这意味着没有监控者的许可，接受者是不能独自完成重构工作的，这从另一个角度说明了方案的安全性。

为什么要考虑这种量子通道，以方案3 为例说明这个问题。在CBRQC 方案中，有两个分别具有算子U 和V 的发送方和一个控制者，从而CBRQC 方案3 应至少有五方（两个发送方、两个接收方和一个控制方，以确保双向传输和控制），因此，需要至少一个五粒子纠缠信道来执行该CBRQC 方案。更重要的是，除了团簇态同时具有GHZ 态和W 类纠缠态的性质外，还具有一些独特的特性，如具有很大的纠缠持久性等。此外，团簇态是基于测量的量子计算的关键组成部分，并已提出了这种态的产生与应用[34-35]。显然，本方案雇佣的局部操作是单量子算子、双量子受控非门和Bell 态测量等，这些操作在诸如腔QED 系统[36]、离子阱系统[37]、光学系统[38]等都可实现。因此按目前的实验技术，本方案是完全可行的。

综上所述，本文结合量子算子远程执行和双向受控隐形传态的思想，提出了四种CBRQC 方案。前两种方案对于任意的单粒子算子对的传输是概率的，而其他方案则是确定性的。然而，经过深入研究发现，如果被传输的算子对(U,V)选自限制集，则方案成功概率和效率都可以显著提高。此外，一些局部操作的减少可能会导致上述两个指标的大幅减少。从量子和经典资源消耗、必要的操作复杂性、成功概率和效率五个方面对不同情况下的方案进行了具体比较，发现最后一种方案是确定性的，且比其他方案更为优化。此外，指出了本方案是安全可行。