基于流固耦合的磁流变减振器特性分析

侯锁军，赵向阳

基于流固耦合的磁流变减振器特性分析

侯锁军，赵向阳

（河南工学院 车辆与交通工程学院，河南 新乡 453003）

针对磁流变减振器示功特性出现畸形的问题，首先采用Hypermesh软件建立磁流变减振器的液体模型和固体模型，将模型导入ADIAN液固耦合软件并建立流固耦合模型，并通过减振器台架示功特性试验验证了流固耦合模型的正确性；采用该流固耦合模型分析了不同速度、不同磁场及不同氮气压力下的内部速度分布和压力分布，通过对不同氮气室压力的减振器内部压力场仿真，合理选择了磁流变减振器内的氮气压力，避免了减振器示功特性出现畸形。这一磁流变减振器特性分析方法为避免磁流变减振器示功特性出现畸形提供了理论依据。

流固耦合；磁流变减振器；台架试验；内特性

磁流变减振器的内特性是指其内部压力及流速特性等，外特性指减振器的示功特性以及速度特性。磁流变减振器的性能设计需要工程师对减振器的结构进行反复调整才能获得合理的减振器外特性曲线，因为外特性畸变的减振器必然会影响其与悬架匹配的工作质量，因此合理选择减振器结构参数来避免减振器外特性畸变是减振器设计的重要内容[1]。有学者对普通减振器外特性的各种畸变及原因做了分析[2]，这对磁流变减振器的设计有一定的参考意义。

磁流变减振器是一种新型的阻尼可调减振器，利用磁流变液的粘度可控特性，能实现减振器阻尼力连续可调，以满足汽车行驶时不同工况下的减振要求[3-6]。磁流变减振器相对于普通减振器，其内外腔灌装磁流变液体粘度大，根据台架试验可知，如果其氮气室压力选择不合理，就会出现减振器外特性畸形现象，影响其与悬架的匹配质量。

本文拟通过流固耦合有限元理论建立磁流变减振器的流固耦合模型，研究磁流变减振器的内部流场及压力分布，为合理选择减振器的氮气压力，充分调试磁流变减振器的特性曲线提供理论参考。

1 流固耦合有限元理论

自动动态增量非线性分析（Automatic Dynamic Incremental Nonlinear Analysis，ADINA）软件[7]是美国ADINA R&D公司开发的有限元通用分析仿真软件，目前在各个工业领域应用非常广泛。ADINA软件可解决多种物理场耦合的问题，如流固耦合、热力耦合、流固热耦合、声流体和结构耦合等。ADINA提供的gap边界条件、参数化动网格、自适应动网格、网格重画分、强耦合等技术为减振器的流固耦合仿真提供了可靠的技术保障。同时，ADINA还具有稳定的非线性问题求解专利技术。

减振器的工作频率一般低于50Hz，其内部油液与结构之间的耦合属于低频动态边界条件耦合问题，流固耦合边界上的基本运动学和动力学条件是：

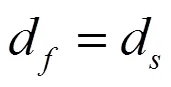
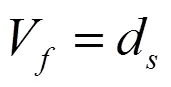
上式对应的条件为非滑移边界，对应滑移边界，上式变为：

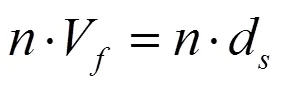
液固耦合计算过程中，液体作用于耦合边界的力为：

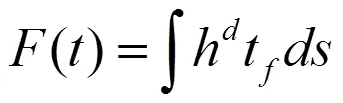
一般来说，在流固耦合分析中，为了得到更好的网格质量和模拟精度，常常使用动网格技术（ALE），对于不可压缩流体，其N-S方程为：

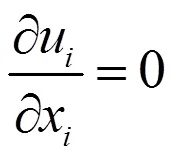
上式为其连续性方程，其动量方程为

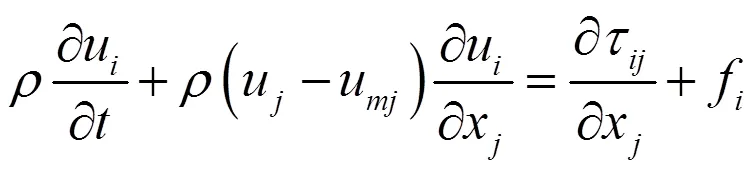
如图1所示，在流固耦合有限元分析中，液体单元和固体单元在流固耦合边界相互作用，该作用导致流固耦合面是可变的，因此网格必须具有变形能力，否则网格易出现扭曲现象而导致计算终止，通常可以利用动网格技术解决这一问题。

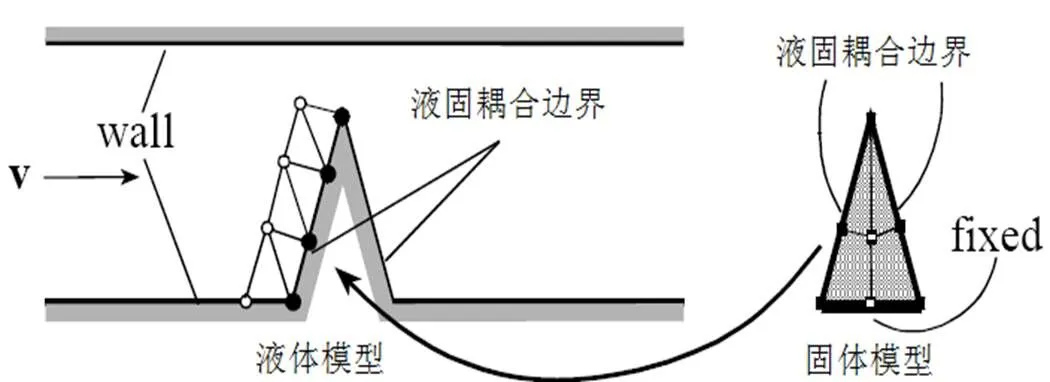
图1 流固耦合模型简图

在利用有限元软件处理流固耦合问题时，分别构建液体和固体模型，其耦合关系通过定义耦合边界条件实现，在软件中分别定义固体模型和液体模型不同的材料、边界条件、流固耦合面、载荷及时间步长等。任何可能与流体发生相互作用的边界都需要定义为FSI边界，有些边界在计算开始时可能没有与液体接触，但在一段时间以后会和液体接触，这些在流固耦合计算过程中所有可能与液体接触的面都要设置为流固耦合面。

2 磁流变减振器流固耦合模型建立

2.1 磁流变减振器结构模型

在建立流固耦合有限元模型之前，首先建立磁流变减振器的三维CATIA模型，如图2所示。该模型在原有CAD模型的基础上做了一些简化，将减振器外筒和上下端盖合成一体，去掉了螺栓孔、密封圈以及紧定螺钉等。

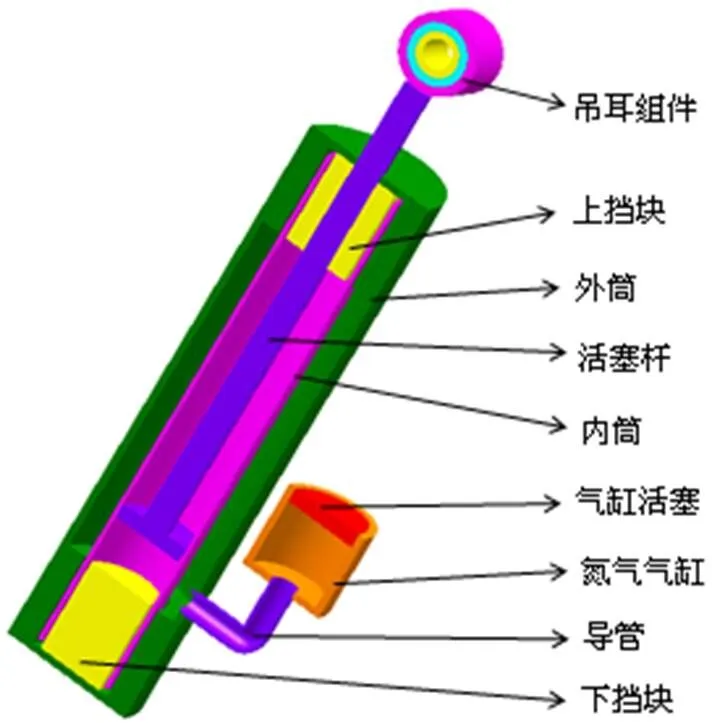
图2 磁流变减振器三维模型

2.2 磁流变减振器流固耦合模型建立

磁流变减振器流固耦合仿真过程中壳体的变形对减振器的运动特性可以忽略不计，只考虑内筒活塞和氮气室活塞的运动特性对减振器特性的影响。磁流变减振器氮气室内气体对氮气室活塞的压力可认为是线性的，在0～10MPa压力范围和0～200℃温度范围内，氮气可认为是理想气体，氮气在磁流变减振器中的工作过程可认为是绝热过程，因此在流固耦合模型中，氮气可用弹簧单元代替。根据公式（6）可计算出氮气室活塞处于中间行程压力为1MPa时的氮气弹簧特性，如图3所示。氮气室的压力P可表示为：

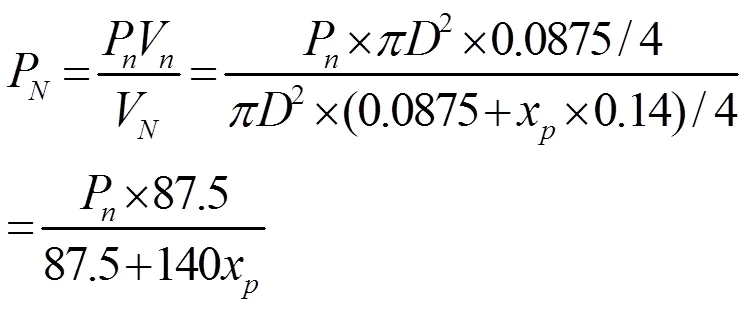
式中，Pn表示氮气室活塞处于中间行程时的压力（Pa），Vn表示氮气室活塞处于中间行程时的氮气室体积（m3），VN表示活塞处于任意位置时的氮气室体积（m3），xp表示氮气室活塞位移（m）。

将磁流变减振器建立的三维CATIA模型以IGS的格式导入有限元前处理软件Hypermesh中，在Hypermesh软件中分别建立固体网格模型和液体网格模型。

固体模型仅仅需要活塞杆、活塞及氮气活塞的模型，如图4所示；液体模型是基于磁流变减振器的三维CATIA固体模型而建立，在Hypermesh软件中画出固体模型所包围的液体部分，如图5所示，其中上通道液体模型和下通道液体模型为受磁场控制的部分。固体和液体模型共102 475个六面体网格，划分网格后给每个零件组赋予材料属性，然后存储成nas格式导入流固耦合ADINA软件中，在ADINA软件中通过Node Set定义壁面、流固耦合面、约束和载荷[8]。

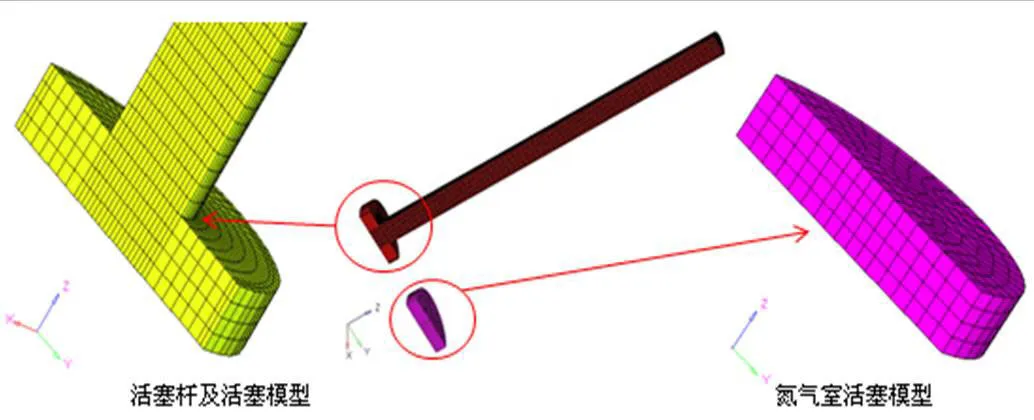
图4 固体网格模型

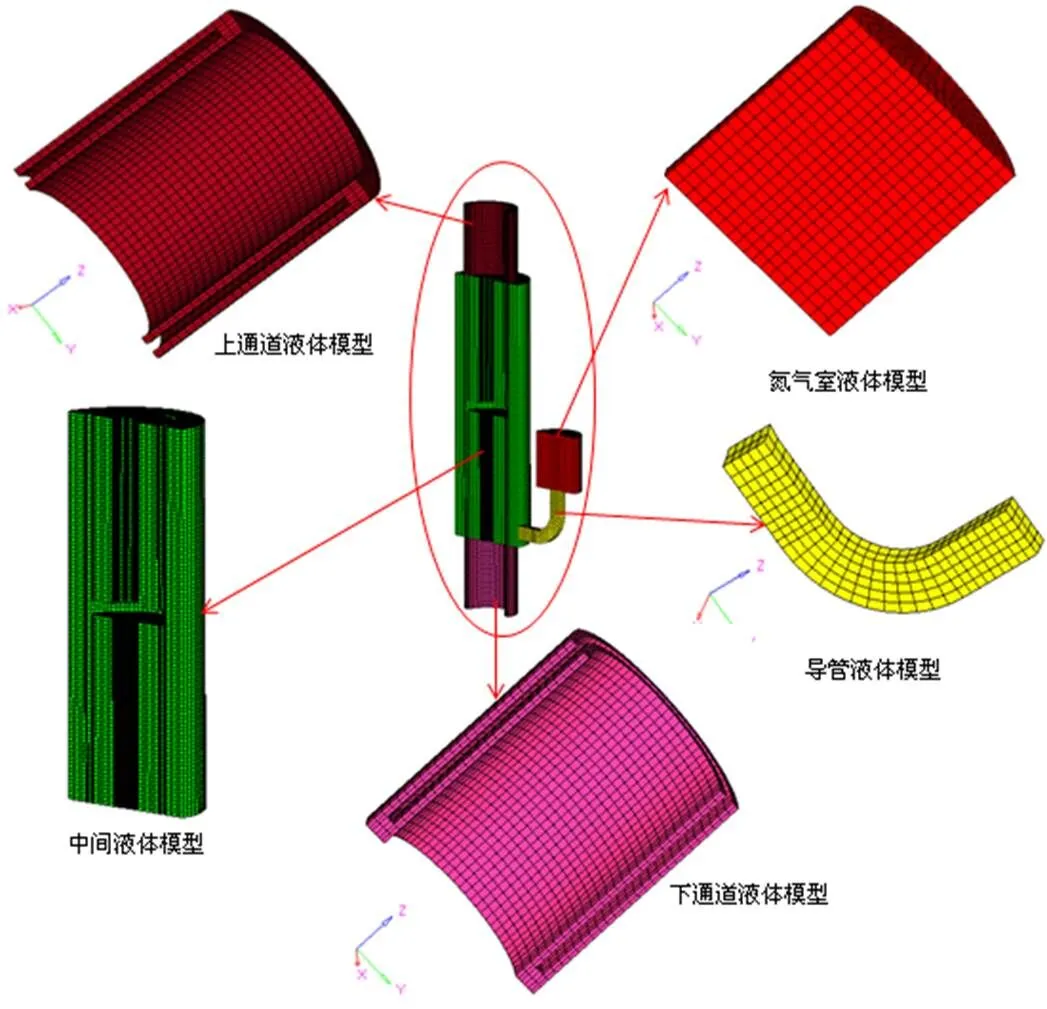
图5 液体网格模型

在固体模型中，活塞杆及活塞材料都为钢，密度为7.8×10-9t/mm3，泊松比为0.29，弹性模量为2.07×105N/mm2；定义载荷时间函数，激励幅值设定为25mm，时间函数按照激励频率设定，如图6所示。约束活塞杆及氮气活塞的运动方向，此模型设定只能在方向运动。设定活塞上端面、活塞下端面和氮气室活塞下端面为耦合面，分别设定为Interface1、Interface2和Interface3，这三个流固耦合面和液体模型中设定的耦合面要一一对应。定义弹簧单元并设定弹簧刚度，如图7所示。

在液体模型中依次定义磁流变液材料参数、流固耦合面、壁面及位移约束面等，如图8所示。磁流变液动力粘度为2.9×10-7MPa.s，密度为2.8×10-9t/mm3。在ADINA流固耦合计算过程中载荷在固体模型中设置，计算时间步长取决于液体模型中的时间步长，因此时间步长在液体模型中设置。

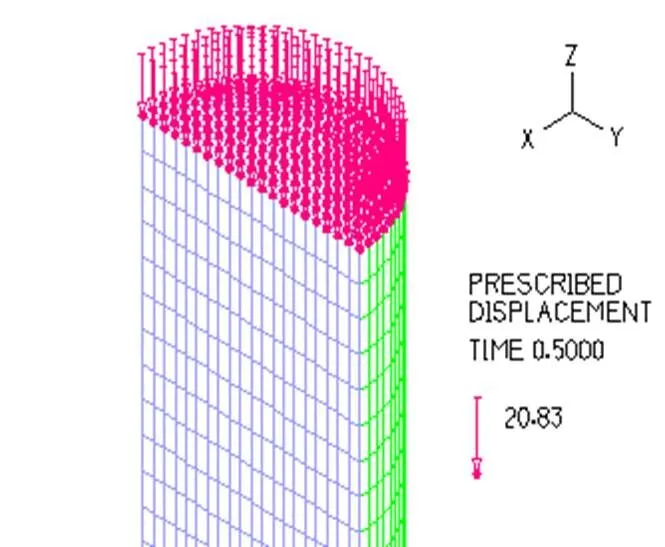
图6 活塞杆上端面位移载荷

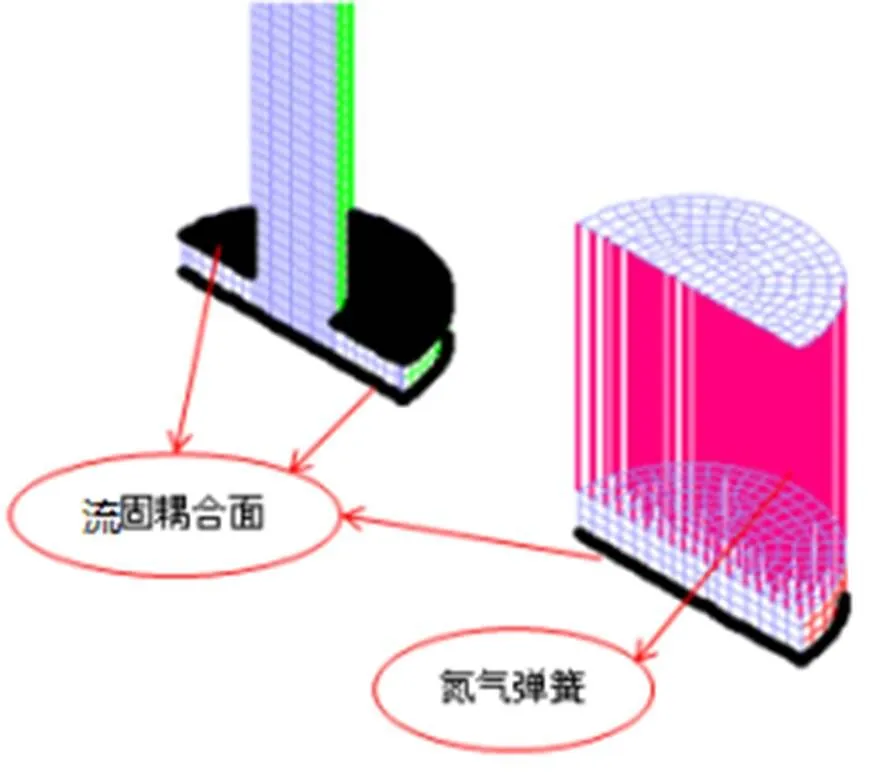
图7 流固耦合面及氮气弹簧

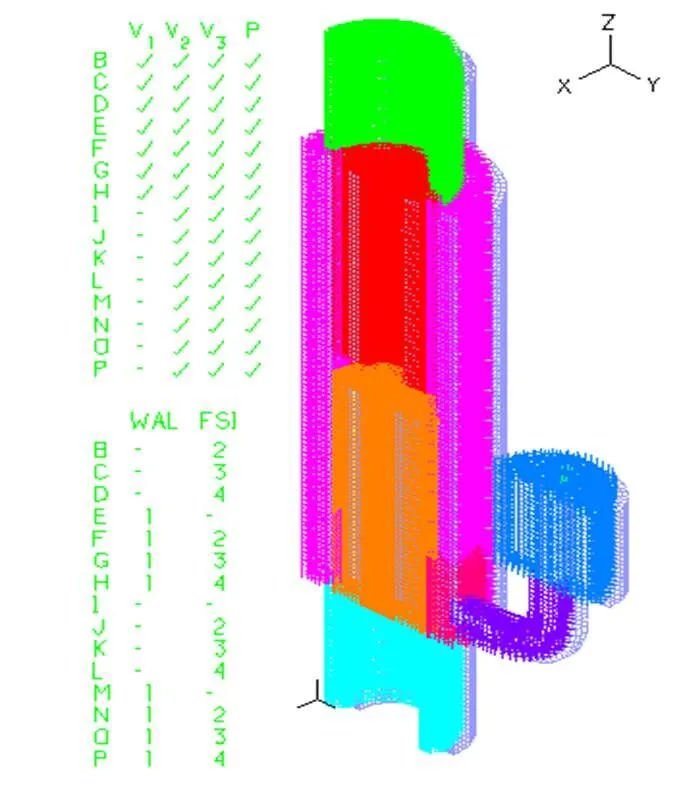
图8 液体模型Wall和FSI边界条件

3 磁流变减振器流固耦合模型验证

流固耦合模型的几点假设：从磁流变液的试验中发现，温度对磁流变液的粘度和剪切应力的影响可以忽略不计，因此模型中不考虑温度对减振器的影响，为了避免橡胶衬套的弹性影响示功曲线的形状，在流固耦合模型中去掉了减振器两端吊耳内的橡胶衬套，工作间隙定为1.5mm，上下端阻尼通道单侧长度均为30mm，激励振幅选择为25mm，激励频率选择0.33Hz、0.83Hz、1.66Hz、2.48Hz和3.33Hz，对应的减振器最大速度分别为0.052m/s、0.13m/s、0.26m/s、0.39m/s和0.52m/s。

图9所示为激励频率1.66Hz不同电流下的示功特性曲线，图10所示为不同激励频率不同电流下的速度特性曲线，可以看出，理论值与试验值大小、趋势一致。由于台架自身存在不稳定性、台架传感器测试精度存在误差以及磁流变减振器制造和安装工艺的误差，使得数据存在一定波动，因此仿真与试验存在一定的误差，不同工况下的仿真值和试验值阻尼力最大差值小于125N，最大误差为4.5%。

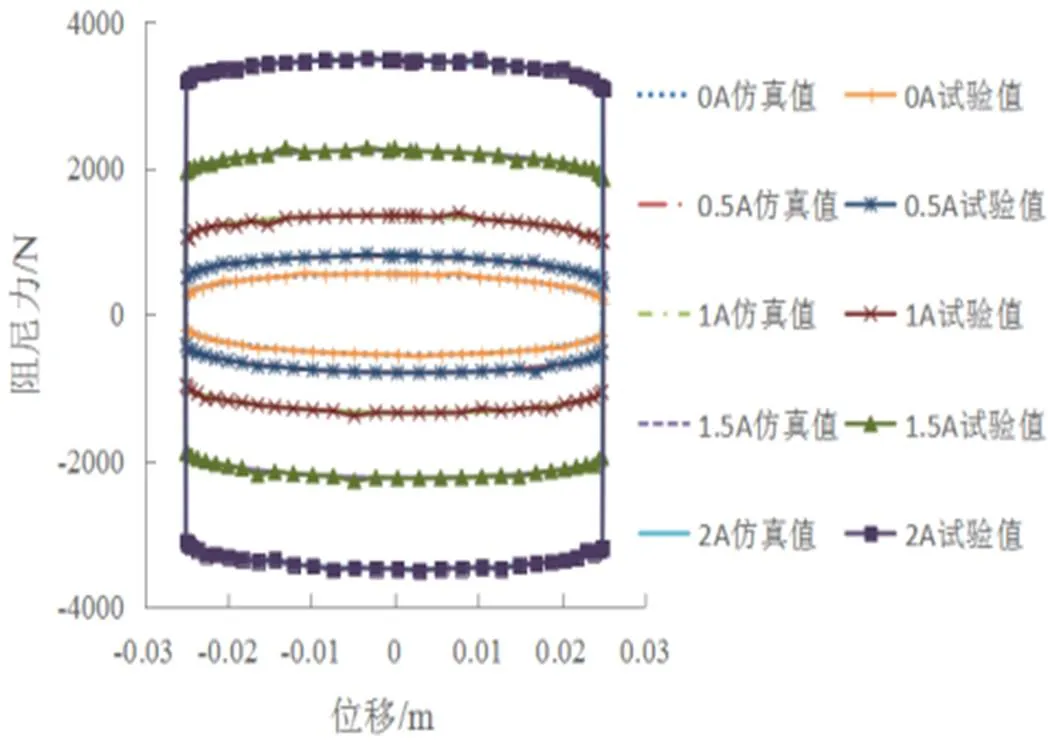
图9 磁流变减振器示功特性仿真和试验结果

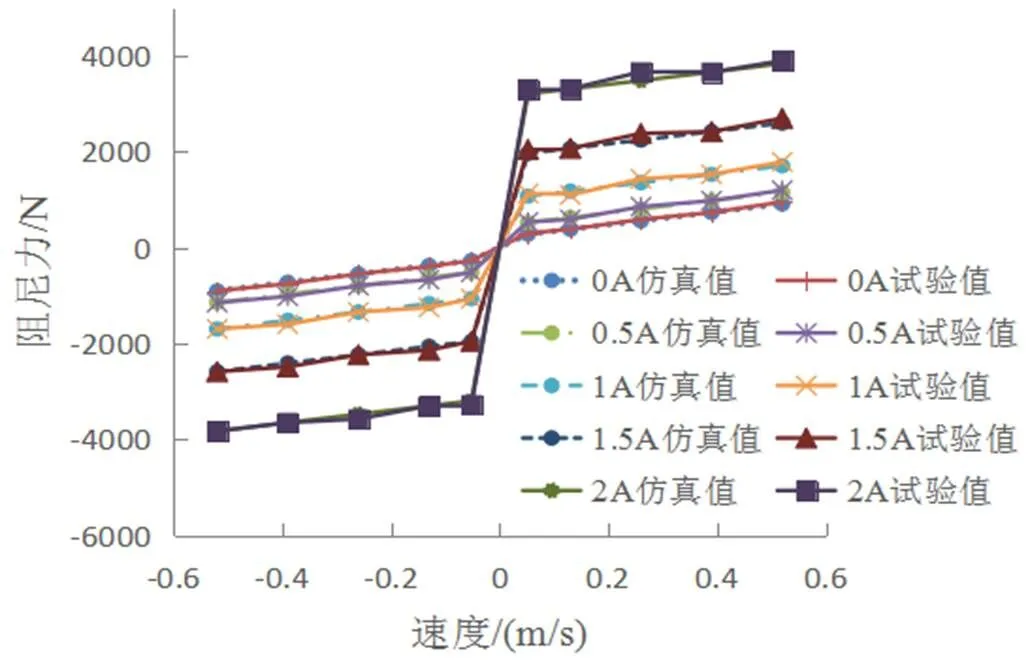
图10 磁流变减振器速度特性仿真和试验结果

4 磁流变减振器内特性分析

4.1 不同速度下流场及压力场分布

对比磁流变减振器工作频率分别为0.33Hz、1.66Hz和3.33Hz下减振器内部液体流动速度分布及压力分布，其他设定条件为氮气压力1MPa，阻尼通道上下端粘度设定为100Pa.s，相当于1A的电流，其他部分粘度设置为0.29Pa.s，图11～16所示为活塞处于拉伸行程中间位置时三种频率下的速度分布图。

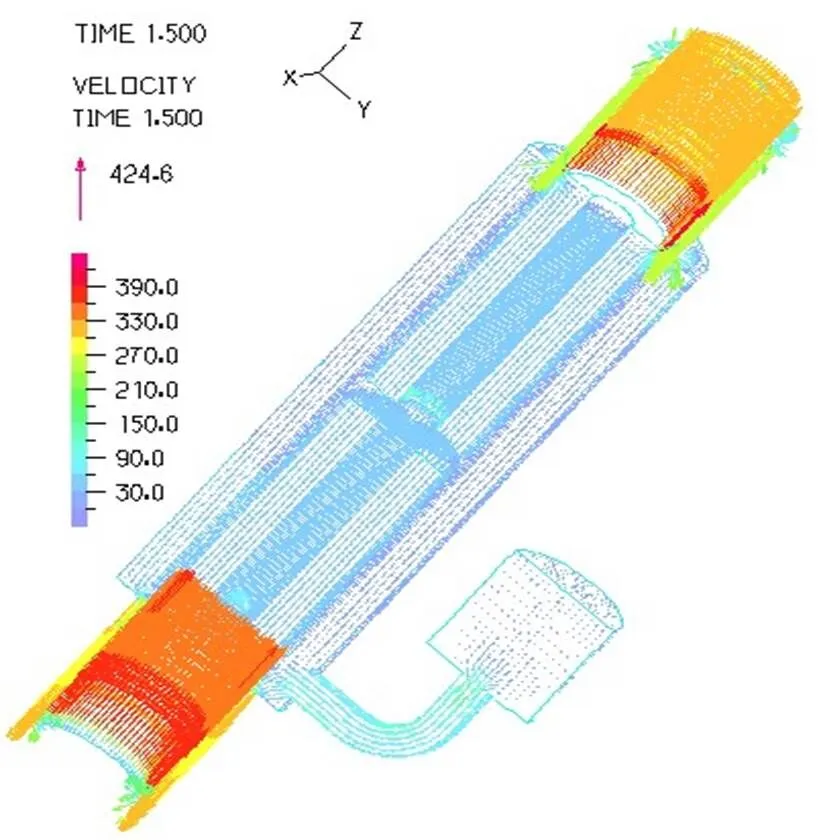
图11 0.33Hz速度三维分布

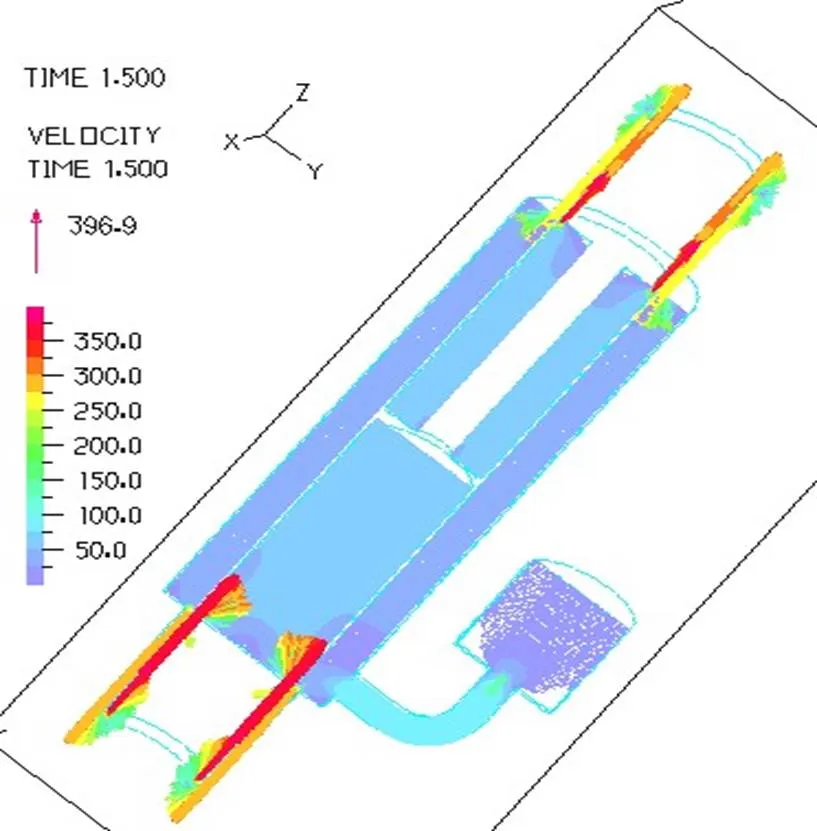
图12 0.33Hz速度截面分布

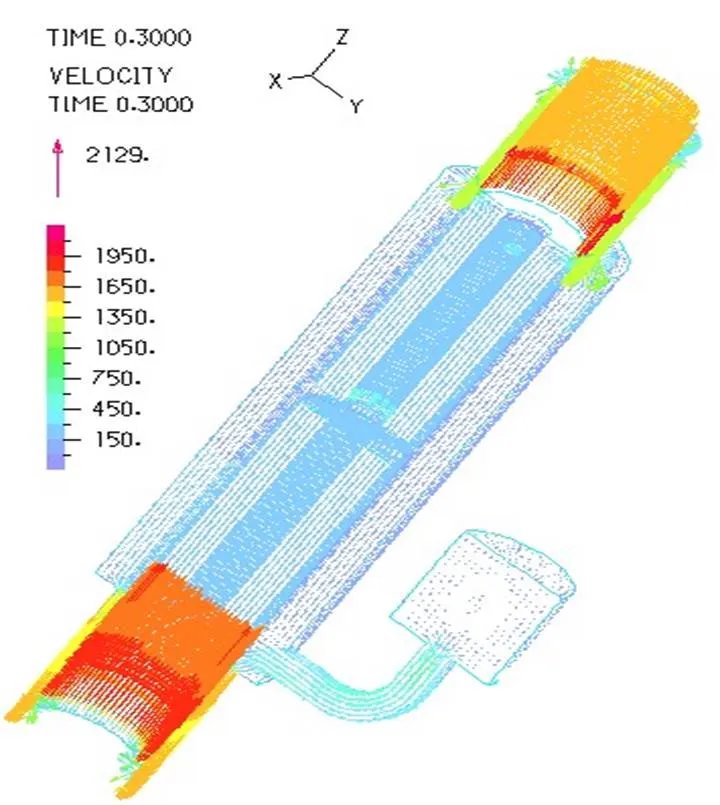
图13 1.66Hz速度三维分布

图14 1.66Hz速度截面分布

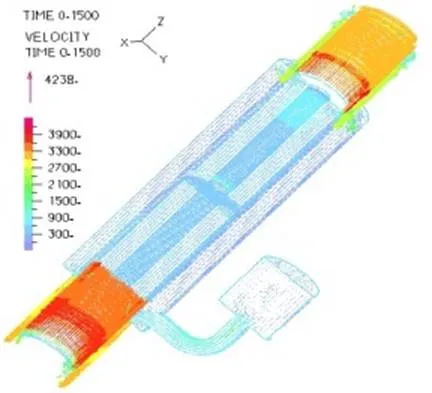
图15 3.33Hz速度三维分布

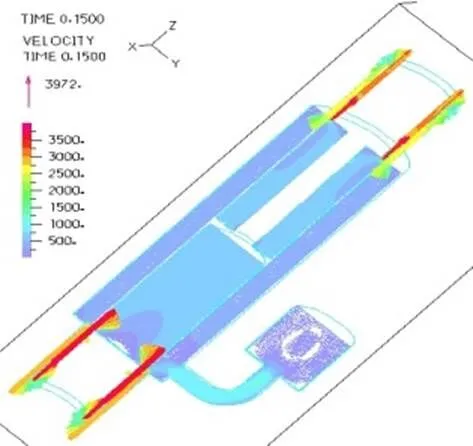
图16 3.33Hz速度截面分布

由图11～16可以看出，活塞带动其上方磁流变液流入顶端环形通道，在环形通道入口处，通道面积减小，形成挤流，流速增加，不同活塞速度下，顶端环形通道的流动速度不同，活塞运动频率越大，环形通道液体流动速度越大。仿真结果也符合这一规律。

图17为0.33Hz、1.66Hz和3.33Hz三种频率下减振器不同部分的粘度值。图18～20所示为0.33Hz、1.66Hz和3.33Hz三种频率下活塞处于拉伸中间行程的压力分布图。可以看出活塞上端到环形通道之间的液体压力均匀分布，大小变化不明显；而在上下端环形阻尼通道处，由于流通面积减小，其液体流动速度增大，液体压力迅速减小，并且在环形通道处液体压力呈梯度减小。随着激励频率的增加，液体流经环形通道后压力下降幅值逐渐增大，三种频率下，上端通道压力降分别为0.234MPa、0.400MPa和0.800MPa；下端通道压力降分别为0.233MPa、0.400MPa和0.760MPa，频率越大阻尼通道压差越大，活塞杆拉伸的阻力就越大。

图17 粘度分布

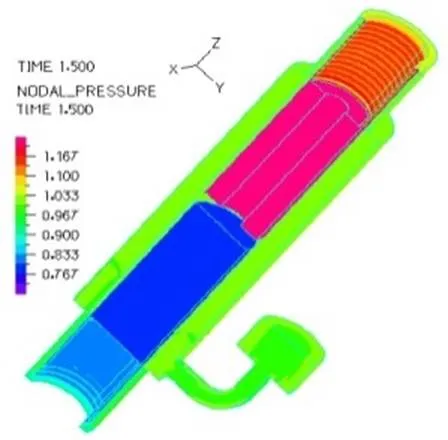
图18 0.33Hz压力分布

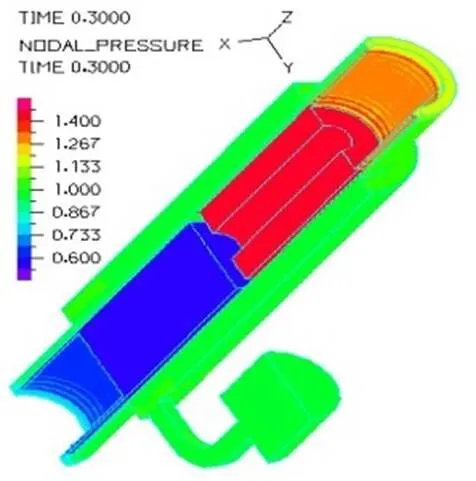
图19 1.66Hz压力分布

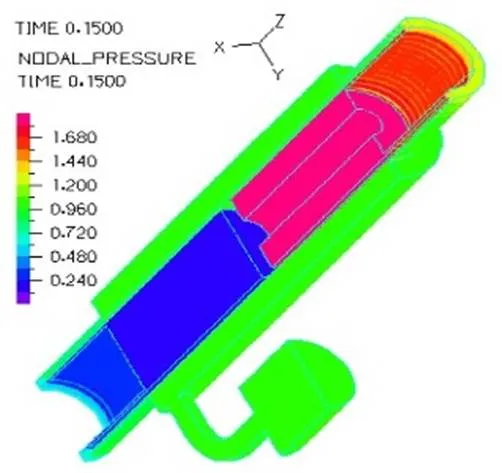
图20 3.33Hz压力分布

4.2 不同磁场下流场及压力场分布

对比磁流变减振器上下端线圈施加磁场（上下端阻尼通道液体粘度设定为100Pa.s，相当于1A电流，其余部分为0.29Pa.s）和不施加磁场下（液体粘度全部设定为0.29Pa.s）的内部液体流场及压力分布，其他设定条件为减振器激励频率为3.33Hz，氮气压力为1MPa。有图21和22所示，零磁场下和施加磁场下速度分布一致；由图23～26可以看出，零磁场与施加磁场两种情况下磁流变液流过上端阻尼通道后压力降分别为0.24MPa和0.750MPa，零磁场与施加磁场两种情况下磁流变液流过下端通道后压力降分别为0.23MPa和0.748MPa。施加磁场后液体流经环形通道后压力下降值明显增大，因此通过磁场控制磁流变液黏度可以实现对磁流变减振器阻尼力的控制。

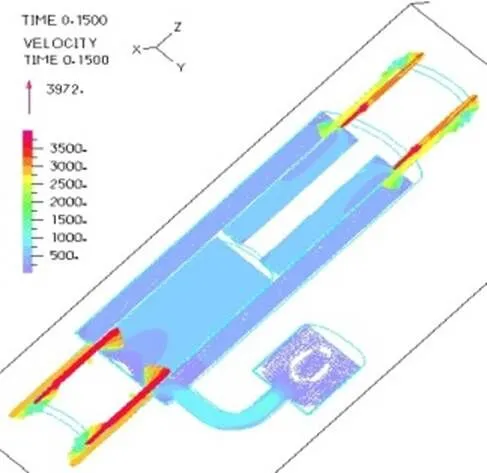
图21 不加磁场流场分布

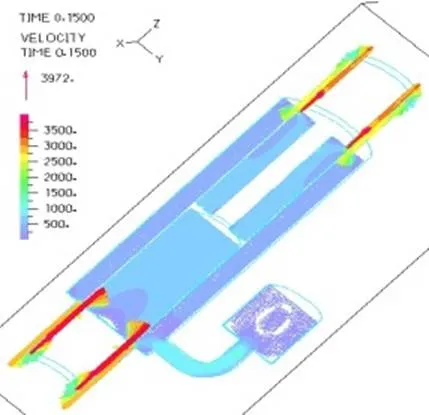
图22 施加磁场流场分布

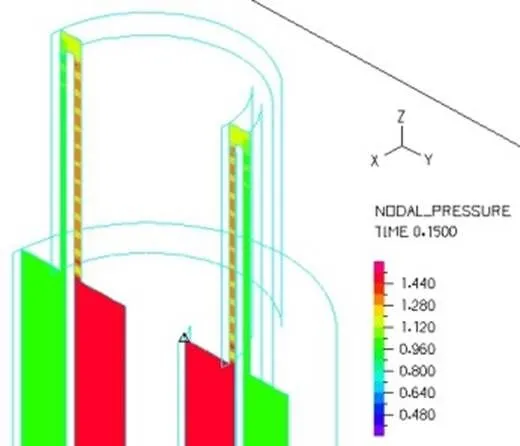
图23 不加磁场上端通道压力截面分布

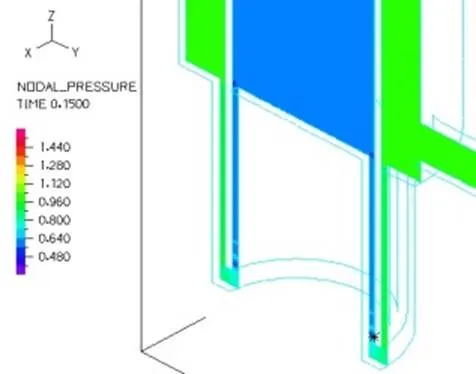
图24 不加磁场下端通道压力截面分布

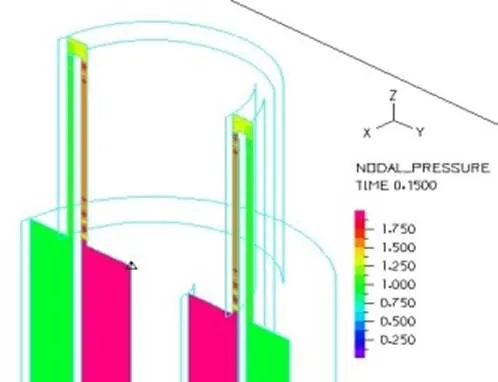
图25 施加磁场上端通道压力截面分布

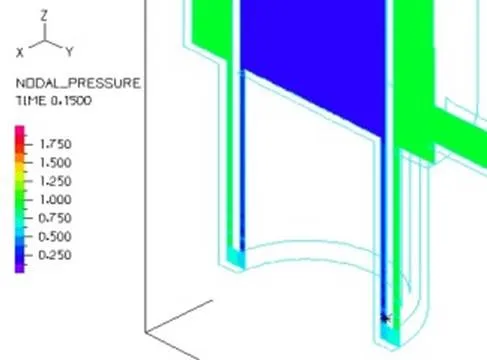
图26 施加磁场下端通道压力截面分布

4.3 不同氮气压力作用下磁流变减振器压力场及流速分布

对比激振频率为1.66Hz，上下端阻尼通道粘度为100Pa.s，相当于磁场线圈施加1A电流，其他部分液体粘度为0.29Pa.s，氮气压力分别为0、0.5和1MPa时，磁流变减振器的流速及压力分布如图27和28所示。从图27速度分布图看，活塞处于拉伸行程中间位置时，活塞上方液体在上端阻尼通道入口处形成挤流，由上端阻尼通道处流向内外缸筒之间，然后液体由下端阻尼通道流入活塞下端空腔，并在下端阻尼通道出口处形成旋流。从速度分布图可以看出，其速度分布合理，并且不同氮气压力下速度分布形态相似。

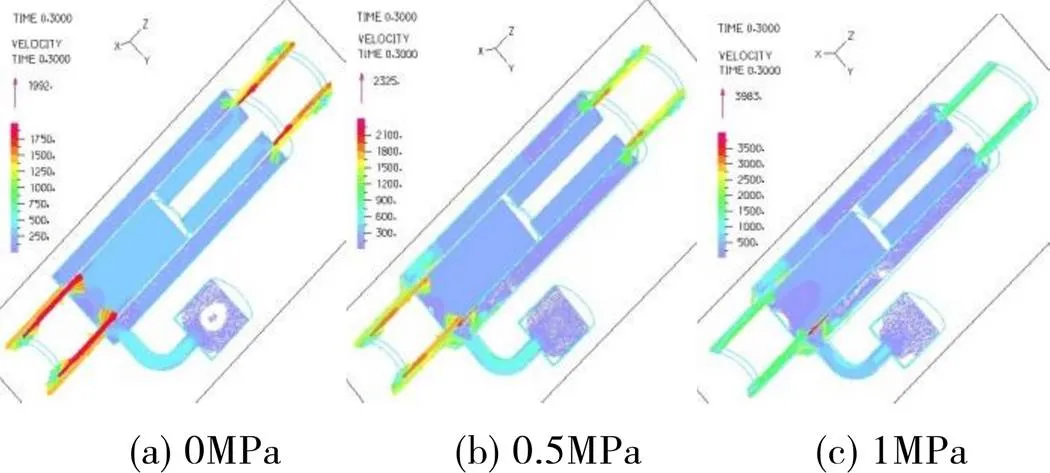
图27 速度分布

由压力分布图28可以看出，在氮气压力为0时，活塞下方的压力为负值；氮气压力为0.5MPa时，下方压力为0.0667MPa；氮气压力增加到1MPa时，下方压力增加到大约0.6MPa。结果表明，没有氮气压力或氮气压力较低时减振器的示功图都会出现畸形，该仿真结果为选择合理的氮气压力提供了理论依据。

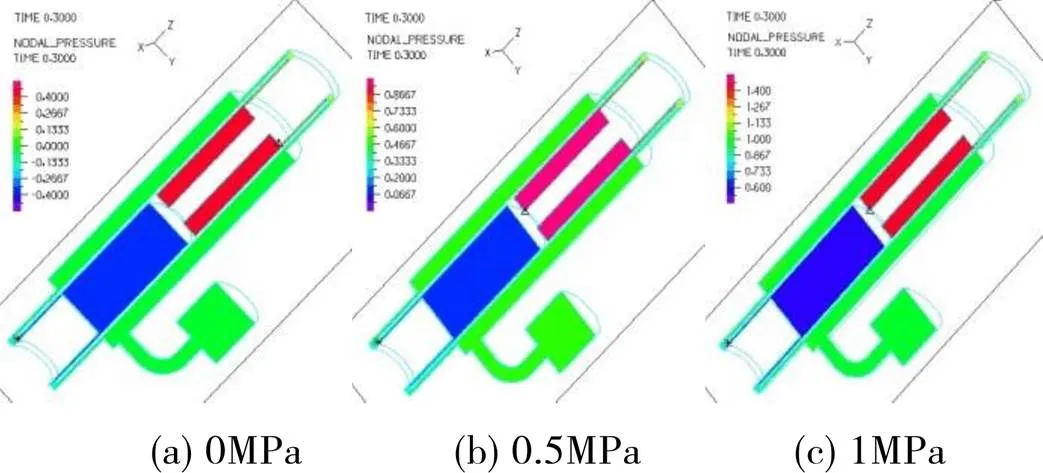
图28 压力分布

图29为磁流变减振器在不同氮气压力下的试验示功曲线，可以看出在氮气压力为0时，示功曲线出现畸形，曲线左上端和右下端出现凹陷现象，其原因是在拉伸行程中磁流变液体不能迅速流回活塞下腔，在压缩行程中磁流变液体不能迅速流回活塞上腔，导致在拉伸和压缩行程初期，出现空行程状态，从而使示功曲线出现畸形现象；当氮气压力为0.5MPa时，凹陷减小；当氮气压力提高到1MPa时，凹陷现象逐渐消失。此试验结果也验证了流固耦合有限元仿真结果。根据不同工况下反复试验的结果，最终确定磁流变减振器的氮气压力为1MPa。

图29 不同氮气压力磁流变减振器示功特性曲线

5 结论

（1）本文通过流固耦合有限元分析软件ADINA建立了磁流变减振器的流固耦合模型，仿真分析了不同速度、不同磁场、不同氮气压力下的减振器速度场和压力场分布，仿真结果符合减振器实际内部液体运动规律。

（2）通过对不同氮气室压力作用下的减振器内部压力场仿真分析，合理选择了磁流变减振器内的氮气压力，避免了减振器示功特性出现畸形现象，为磁流变减振器氮气压力的选择提供了理论依据。

[1] 孙胜利.位移相关减振器动力学建模及对车辆性能影响的研究[D].长春：吉林大学,2008.

[2] 俞德孚.车辆悬架减振器的理论和实践[M].北京：兵器工业出版社,2003.

[3] 刘韶庆. 磁流变可调阻尼减振器的特性研究[D]. 镇江: 江苏大学, 2007.

[4] WERELEY N M, CHO J U, CHOI Y T, et al. Magnetorheological dampers in shear mode [J]. Smart materials and structures, 2008, 17(1): 1-11.

[5] HONG S R, CHOI S B, CHOI Y T, et al. Non-dimensional analysis and design of a magnetorheological damper[J]. Journal of sound and vibration, 2005, 288(4-5): 847- 863.

[6] 陈杰平.基于磁流变减振器的汽车半主动悬架设计与控制研究[D].合肥:合肥工业大学,2010.

[7] 岳戈,梁宇白,陈晨,等. ADINA流体与流固耦合功能的高级应用[M].北京:人民交通出版社, 2010.

[8] 马野, 袁志丹,曹金凤. ADINA有限元经典实例分析[M]. 北京: 机械工业出版社,2011.

Characteristics Analysis of Magneto-rheological Damper Based on Fluid-solid Coupling

HOU Suo-jun, ZHAO Xiang-yang

(School of Vehicle and Traffic Engineering, Henan Institute of Technology, Xinxiang 453003, China)

In order to solve the problem of abnormal force-displacement characteristics of magneto-rheological(MR) damper, firstly, the fluid model and solid model of MR damper were established by Hyper mesh software, the model was imported into ADINA fluid-solid coupling software to establish the fluid-solid coupling model, and the correctness of the fluid-solid coupling model was verified by the bench test of the force-displacement characteristics of the damper. The fluid-solid coupling model was used to analyze the internal velocity distribution and pressure distribution under different velocity, magnetic field and nitrogen pressure. Through the simulation of the internal pressure field of the MR damper with different nitrogen chamber pressure, the nitrogen pressure in the MR damper was reasonably selected to avoid the deformity of the force-displacement characteristics of the MR damper. The characteristic analysis method of MR damper studied in this paper provides a theoretical basis for avoiding the deformity of the force-displacement characteristic of MR damper.

fluid-solid coupling; MR damper; bench test; internal characteristics

U461.4

A

2096–7772(2020)01–0039–07

2019-12-27

河南省科技攻关项目（182102210034）；河南省高等学校青年骨干教师培养计划项目（2016GGJS-196，2018GCJS172）

侯锁军（1979―），男，河南辉县人，副教授，博士，主要从事汽车系统动力学及悬架控制研究。

（责任编辑吕春红）