基于灵敏度计算和多维泰勒网的随机时变非线性系统辨识

张 超，杨 晓，朱命冬

基于灵敏度计算和多维泰勒网的随机时变非线性系统辨识

张 超1,2，杨 晓1,2，朱命冬3

（1.河南工学院 电气工程与自动化学院，河南 新乡 453003；2.河南省新能源发电关键装备工程研究中心，河南 新乡 453003；3.河南工学院 计算机科学与技术学院，河南 新乡 453003）

针对随机时变非线性系统的建模问题，提出一种基于最优结构多维泰勒网的辨识策略。首先将多维泰勒网权值作为时变参数，由寻求最优步长的增量梯度法进行训练以响应系统输入-输出的快速变化；然后为满足高实时性要求，利用改进的灵敏度计算方法剪除网络冗余输入变量和中间节点，实现最佳的泛化能力；最后用算例仿真结果验证了方案的有效性。

灵敏度计算；增量梯度法；多维泰勒网；非线性系统辨识

0 引言

在机械工程领域，如车桥系统振动、柔性机械臂等问题中，存在大量复杂的非线性因素。此外，各种随机因素的干扰以及系统的时变特殊性均会影响模型分析和建模精度。正是这些复杂多变的因素为系统分析和结构设计带来更多技术上的要求和挑战。为了提高系统模型准确性，尤其是针对结构复杂多样的系统建模，系统辨识成为解决上述技术难题的有效手段。系统辨识是通过输入输出数据对未知系统建模的过程[1]。目前辨识方法主要有：递推最小二乘法(RLS)、最大似然法、阶跃响应法和神经网络法等。例如，文献[2]将RLS算法与Kalman变量相结合构成扩展的RLS算法并应用于系统辨识；文献[3]提出一种快速的最大似然法，借助任意的未知输入来估计脉冲响应。然而以上方法都是以被控对象精确的数学模型为基础，对于非线性系统来说应用困难。非线性系统同线性系统相比更加复杂且难以建模，而神经网络因其自身并行分布、存储和自适应等优势，对这种复杂的、需考虑设计多样性以及已知信息模糊的非线性系统处理尤其适用。例如，文献[4]提出用一种动态时滞模糊小波神经网络模型来辨识系统结构；文献[5]提出用延迟系统及延迟时间的神经网络辨识方法，实现时滞时变系统的有效辨识。但神经网络存在训练时间长、易陷入局部最优的问题。

多维泰勒网(MTN)由于采用多项式型的非线性自回归滑动平均模型，通过借助抽头延迟映射表示动态系统，已成为针对非线性系统动力学建模的有效手段，尤其当非线性系统机理不精确时更加适用。分析MTN模型的多项式函数构成可发现，其多项式由线性项和非线性项两部分组成，以表示一般动力学状态特性，进而是对系统行为的显性描述。MTN在模型预测[6]、系统辨识[7]、灾害预测[8]、电机控制[9]以及非线性控制[10]等领域的应用研究已成为当前热点。

文献[11]利用RLS算法通过递推的方式进行系统辨识并考虑如何消除外界环境的影响(噪声干扰和时变特性)，但该算法存在自适应跟踪速度不快以及辨识精度不高的问题。文献[12]将增量梯度法引入随机时变非线性系统辨识，由于其在每步学习时都寻求最优步长，故可解决在采用步长固定的梯度下降法时收敛速度慢的缺陷，进而可以满足时变系统建模要求。此外，由于实时性是辨识模型应用的关键，MTN模型需要在相对少的节点数下收敛。同时，在实际建模时，系统模型阶次一般情况下都是未知的，因此在确定中间节点规模的同时也要选择好模型阶次即确定合理的模型输入个数，这在模型辨识领域也是极为重要的问题。因此本文采用改进的灵敏度计算方法[13]来剪除网络冗余输入项和冗余中间层回归项，以达到精简网络结构、减少迭代学习时间及改进泛化的目的。

1 问题描述

本文基于MTN模型解决随机时变非线性系统的辨识问题，利用MTN中间层权值作为时变参数，设计快速学习算法以实时响应系统输入-输出的变化并实现MTN模型最佳的泛化能力。

考虑具有噪声干扰的非线性时变离散系统：

2 基于MTN的随机时变非线性系统辨识

引理1[15]任何定义于一个闭区间的连续函数可以用多项式函数任意准确地逼近。

图1 多维泰勒网模型

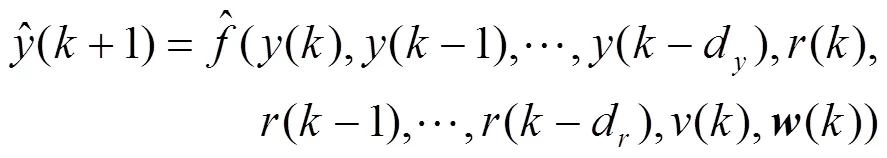
利用网络学习策略，通过改进的梯度下降学习算法实现MTN模型权值的快速更新。

目标函数为：

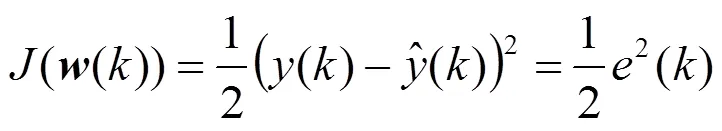
更新方程为：

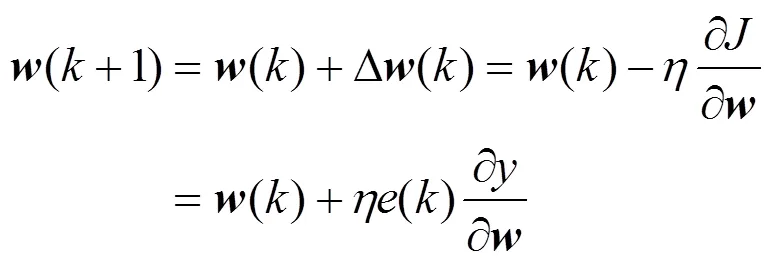
为追求更快的收敛速度，以满足时变系统的建模要求，本部分设计增量梯度法用于随机时变非线性系统辨识，在每步学习时都寻求最优步长。

由于

从而

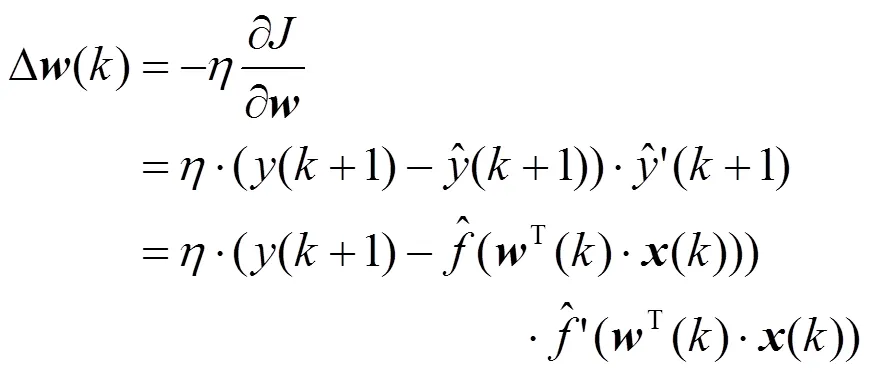
将式(8)代入式(10)，有

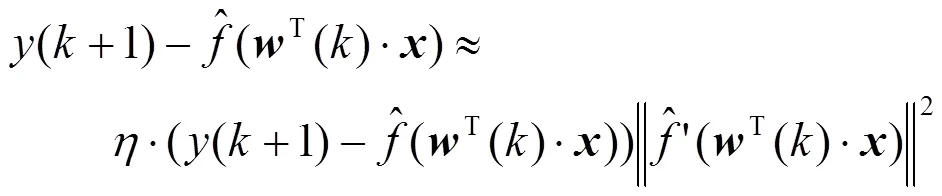
最优步长为：

3 基于灵敏度计算的MTN泛化能力改进

精简的MTN模型将大大减少迭代学习时间并简化网络结构，这有助于工程实践和硬件实现。

灵敏度计算方法是获取最佳泛化能力和最小结构的剪枝算法，可用于剪除冗余的中间节点和不重要的输入变量[13]。在训练辨识网络时，首先计算各输入变量和各中间节点对于待辨识模型的贡献大小，然后经比较后去除灵敏度较小的节点和权值，从而在保证精度的前提下精简网络结构，提出以下测度：

步骤1 使用一阶惯性滤波，即

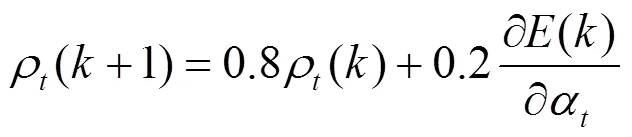
步骤3 取稳态时的灵敏度值。在某段时间内一个节点的归一化灵敏度的标准差和平均值为：

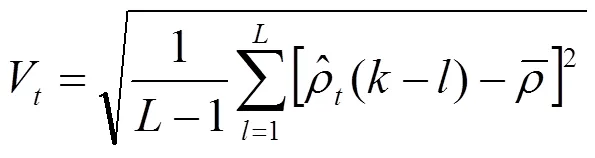
4 算例分析

本节通过对由式(22)表示的随机时变非线性系统的仿真实验来验证所提方法的有效性。

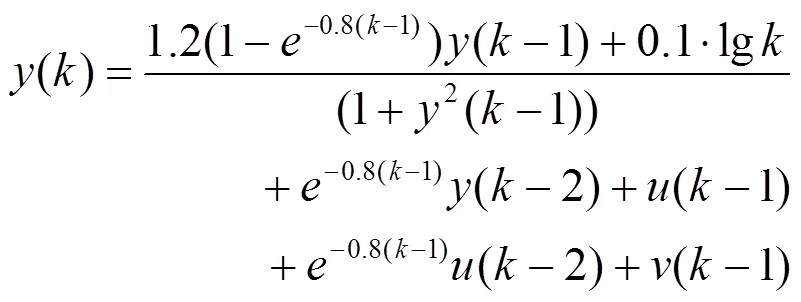
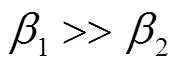
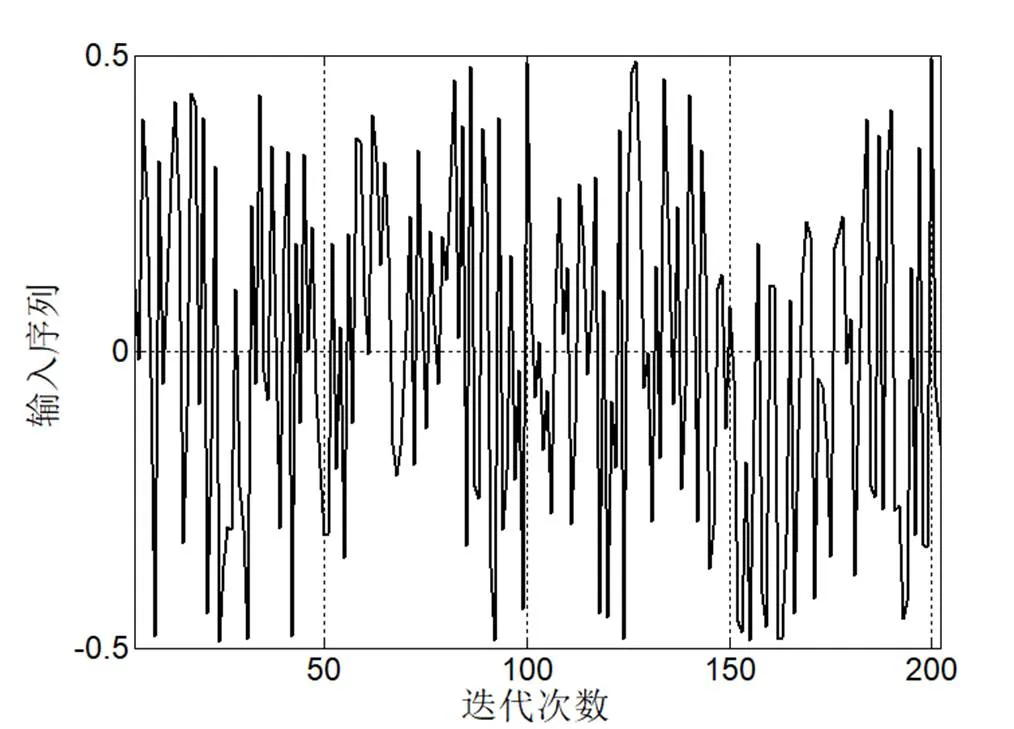
图2 输入信号

图3为剪枝过程中剪除冗余输入变量和中间节点的学习曲线。可见，基于增量梯度法的MTN辨识方案在辨识精度改善方面效果明显。同时，当使用灵敏度计算方法精简MTN网络时训练误差未发生较大波动。

图3 剪除输入变量和中间节点的学习曲线(MSE)

通过式(6)、式(12)以及式(18)~式(21)的充分训练，最终获得结构为4-10-1的精简MTN。表1记录了剪枝过程的辨识参数。算法在841、872、882、898、924、974、1032和1036步删除了冗余中间节点，在875和927步删除了冗余输入变量，最后网络中余下10个中间节点和4个输入变量，这大大降低了计算量和网络的复杂度。

图4 剪枝过程中MTN权值系数的变化(以任意4个中间节点为例)

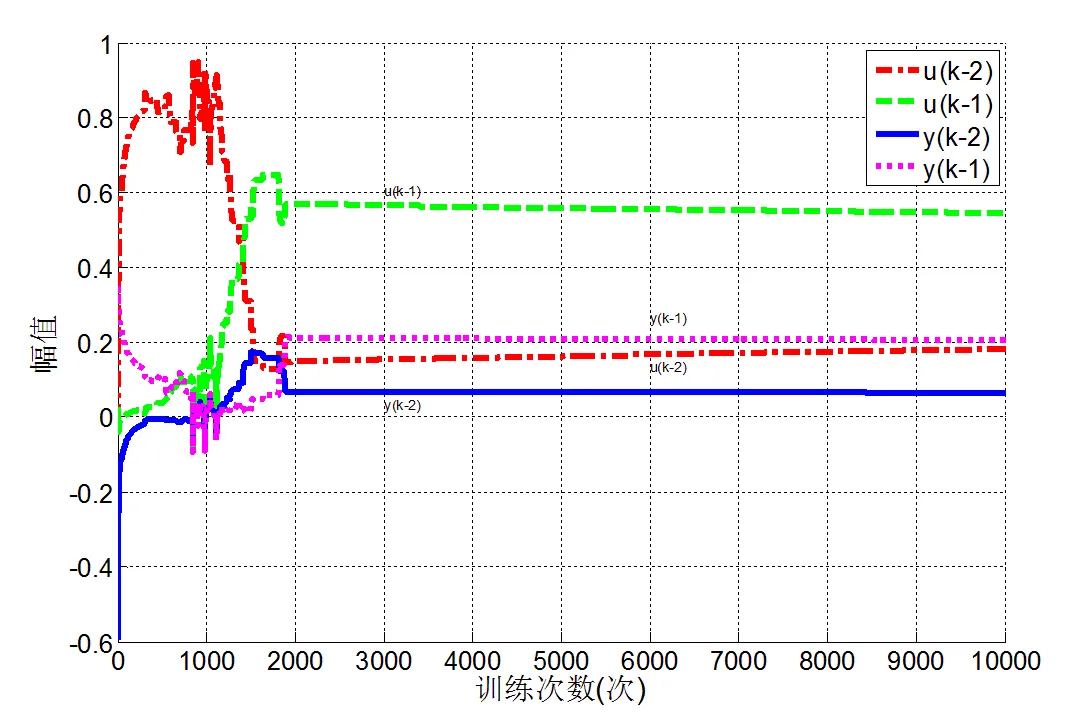
图5 各输入变量的灵敏度变化曲线

表1 辨识参数

此外，对于同样的100个测试样本，剪枝网络(仅有10个有效节点)的测试误差为1.6013，原有网络(84个中间节点)的测试误差为1.5534。基本无差别的误差对比结果验证了方案的有效性。可见，基于增量梯度法和灵敏度计算混合算法的MTN辨识方法实现了网络最简结构，简化了网络系统动态建模，有效推进了MTN在实际工程中的进一步运用。

5 结束语

鉴于随机时变非线性系统辨识问题的研究具有显著的工程价值和理论意义，本文提出了一种以多维泰勒网的连接权值作为时变参数，由增量梯度法和灵敏度计算混合算法进行训练，从而实现最优结构的MTN辨识方案。该方案在确保响应系统输入-输出快速变化的前提下，可降低计算复杂度，满足高实时性能，最终实现随机时变非线性系统的有效辨识。仿真结果表明，所提方案能够保证建模精度并可实现网络最佳泛化能力，是可行和有效的。

[1] UGALDE H M R, CARMONA J C, REYES-REYES J, et al. Balanced simplicity-accuracy neural network model families for system identification[J]. Neural computing and applications,2015,26(1):171-186.

[2] 邱亚,李鑫,陈薇.基于RLS和EKF算法的全钒液流电池SOC估计[J].控制与决策,2018,33(1):37-44.

[3] 杨雅君,郑宇昕,廖瑛.一类参数线性系统辨识的最优输入设计[J].控制理论与应用,2016,33(7):889-896.

[4] JIANG X M, MAHADEVAN S, YUYAN Y. Fuzzy stochastic neural network model for structural system identification[J]. Mechanical systems and signal processing, 2017, 2: 394-411.

[5] 章心忆.下肢外骨骼机器人的建模和控制策略研究[D].南京: 南京理工大学,2017.

[6] 周博,严洪森.一类具有羊群效应的多重多维泰勒网动力学模型[J].控制理论与应用,2015,32(7):963-969.

[7] 张超,严洪森.基于最优结构多维泰勒网的含噪声非线性时变系统辨识[J].东南大学学报(自然科学版),2017,47(6): 1086-1093.

[8] 林屹,严洪森.多尺度正负反馈交替论模型及其应用[J]. 控制理论与应用,2016,33(7): 879-888.

[9] ZHANG C, YAN H S. Inverse control of multi-dimensional Taylor network for permanent magnet synchronous motor[J]. COMPEL-The international journal for computation and mathematics in electrical and electronic engineering, 2017,36(6):1676-1689.

[10] YAN H S, KANG A M. Asymptotic tracking and dynamic regulation of SISO non-linear system based on discrete multi-dimensional Taylor network[J]. IET control theory and applications,2017,11(10):1619-1626.

[11] LI J, ZHENG Y, LIN Z. Recursive identification of time-varying systems: Self-tuning and matrix RLS algorithms[J]. Systems and control letters,2014,66: 104-110.

[12] VARAGNOLO D, ZANELLA F, CENEDESE A, et al. Newton-Raphson consensus for distributed convex optimization[J]. IEEE Transactions on Automatic Control, 2016, 61(4): 994-1009.

[13] ZHANG C, WEI H, XIE L, et al. Direct interval forecasting of wind speed using radial basis function neural networks in a multi-objective optimization framework[J]. Neurocomputing, 2016, 205: 53-63.

[14] 朱红路. 热工信号自适应滤波及其在建模与控制中的应用[D].北京:华北电力大学,2010.

[15] KLAMBAUER G. Mathematical analysis[M]. New York: Marcel Dekker INC, 1975:236-237.

Identification of Stochastic Time-varying Nonlinear System based on Sensitivity Calculation and Multi-dimensional Taylor Network

ZHANG Chao1,2, YANG Xiao1,2, ZHU Ming-dong3

(1.School of Electrical Engineering and Automation, Henan Institute of Technology, Xinxiang 453003, China; 2.Henan Engineering Research Center of Key Equipment for New Energy Generation, Xinxiang 453003, China; 3.School of Computer Science and Technology, Henan Institute of Technology, Xinxiang 453003, China)

Aiming at the modeling problems of stochastic time-varying nonlinear system, an identification strategy based on the multi-dimensional Taylor network (MTN) with optimal structure is proposed. Firstly, the MTN’s weights are taken as the time-varying parameters, and the incremental gradient method for determining the optimal step size is adopted to train the MTN model to reflect the system’s input-output rapid change. Secondly, to meet the high real-time requirements, the improved sensitivity calculation method is developed to remove the network’s redundant input variables and middle nodes to realize the optimum generalization ability. Finally, the simulation results of an example verify the effectiveness of the scheme.

sensitivity calculation; incremental gradient method; multi-dimensional Taylor network; system identification

N945.14

A

2096–7772(2020)01–0033–06

2019-12-22

国家自然科学基金资助项目（61802116）；河南省重点研发与推广专项（202102110274）；河南省高等学校重点科研项目（16A120011）；河南工学院高层次人才科研启动基金（KQ1863）

张超（1983―），男，河南新乡人，讲师，博士，主要从事智能控制理论与方法研究。

（责任编辑吕春红）