基于压缩感知的稀疏度自适应无源目标定位算法

闫雷兵，王翠钦，牟光臣，尹 川

基于压缩感知的稀疏度自适应无源目标定位算法

闫雷兵1，王翠钦1，牟光臣1，尹 川2

（1.河南工学院 电子信息工程学院，河南 新乡 453003；2.杭州电子科技大学 电子信息学院，浙江 杭州 310018）

鉴于无源目标定位需要采集大量的数据，导致传感器节点能耗过大、使用年限较短，因而基于压缩感知理论，设计了一种稀疏度自适应的无源目标定位算法。首先用一个传感器节点遍历监控区域建立观测字典，从而构建出满足约束等距条件的感知矩阵，然后自适应估算出目标的稀疏度，最后通过正交匹配算法恢复出目标位置向量。实验结果表明，该算法不仅在稀疏度未知的情况下能够估算目标的位置，而且与传统算法相比能够取得更高的定位精度。

无线传感网络；无源定位；压缩感知；稀疏度

0 引言

现有的目标定位技术大都依赖于固定在被定位目标上的特定的终端辅助设备如手机或电子标签[1]，这被称为主动式定位技术[2]。然而在特定的场景下，例如跟踪非法入侵目标、发现被救援目标、监控不特定的野生动物等时，就不可能使用主动式定位技术。而被动式定位，即无源定位（Device Free Localization，DFL）技术，具有被定位目标无需携带辅助设备等优点，在特定场景中能发挥更大的优势。但DFL技术通常需要通过无线传感网络（Wireless Sensor Network，WSN）频繁地采集大量的数据，这就造成WSN能耗过大，使用寿命较短。

压缩感知（Compressed Sensing，CS），也称作压缩采样或稀疏采样，主要是研究采样信号的稀疏特性，当奈奎斯特采样频率远大于采样频率时，利用随机采样获取有限个离散信号样本，通过非线性重构算法可以恢复原始信号。依据CS理论可知，目标定位问题可以转化为信号恢复问题，即快速重建目标位置，这为基于WSN节点对目标的定位提供了理论依据。当前，将CS理论应用于目标定位技术已成为研究热点，且其在DFL技术中的研究已经取得了一些成果，典型的重构算法有基追踪（Basis Pursuit，BP）法[3]和正交匹配追踪（Orthogonal Matching Pursuit，OMP）法[4]，目标的位置向量均能够通过测量向量恢复出来，上述方法均通过测量有限接收信号的强度（Receive Signal Strength，RSS）而组成观测字典，再利用CS的数据重构恢复出目标的实际位置，然而上述方法均需要事先知道信号的稀疏度才能恢复出原信号，稀疏度即被定位目标的个数。在目标个数未知的情况下，基于目标稀疏度的重构定位算法将不再适用，因此近年来许多科研工作者提出了未知稀疏度的重构定位算法，其中比较典型的算法有文献[5]中的贪婪匹配追踪( Greedy Matching Pursuit，GMP)算法，该算法即使事先不知道目标个数也能重构恢复出目标的位置，但是由于测量信道模型的变化，容易造成获取的感知矩阵不满足约束等距(Restricted Isometric Property，RIP )条件[6]，从而造成GMP算法失效。而文献[7]中改进型的GMP算法，利用多分辨率分析的方法不断逼近目标真实位置，使得定位效果得到改善和提升，同时引入了虚警概率和丢失概率来全面地衡量算法的计数性能。文献[8]则利用数学手段，通过对观测字典进行奇异值分解使得到的字典满足约束等距条件，且对观测值的预处理并未影响信号的稀疏度，从而提高了感知矩阵的适用性，为CS理论应用于目标位置重构提供了理论依据。

基于上述方法的研究思路和存在的问题，设计了稀疏度自适应正交匹配追踪算法来恢复目标的位置向量。尽管在信号稀疏度未知的情况下，稀疏度自适应匹配（Sparsity Adaptive Matching Pursuit，SAMP）法[9]能够重构原始信号，但最优步长的选择、计算复杂度的优化以及重构信号的概率都是无法回避的难题。针对SAMP算法面临的问题，设计了稀疏度自适应正交匹配追踪（Sparsity Adaptive Orthogonal Matching Pursuit，SAOMP）算法，该算法主要分为两个阶段：第一阶段估算稀疏度以构建目标位置向量；第二阶段利用第一阶段估算出的稀疏度来构建感知矩阵和观测向量，通过迭代自动获取步长，代入OMP算法重构目标的位置向量。当目标的稀疏度未知时，设计的SAOMP算法能够精确重构出原始信号，即目标的位置向量，该算法较传统算法而言运算量较少、复杂度较低，而且比传统算法具有更高的定位精度。

1 目标定位模型

1.1 定位场景

图1 目标监控区域

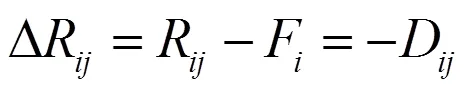
1.2 构建感知矩阵

2 稀疏度自适应正交匹配目标定位算法

2.1 稀疏度估计

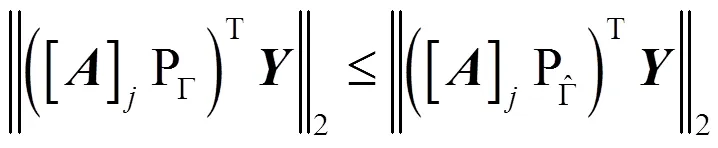
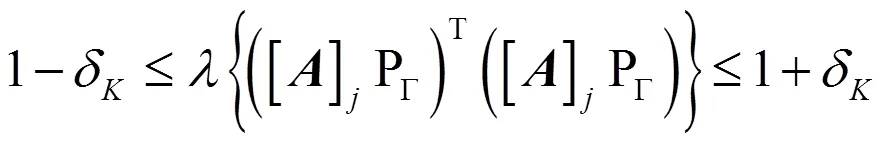
由此可以得到：

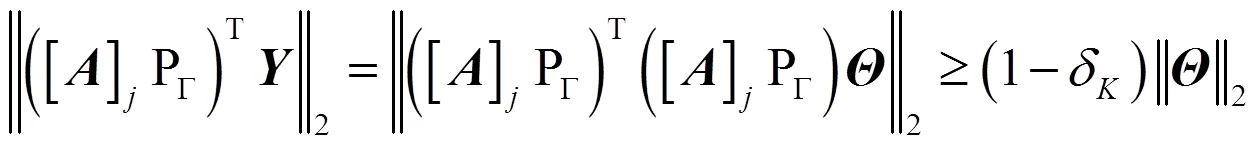
结合式（7）与式（10），整理得到：

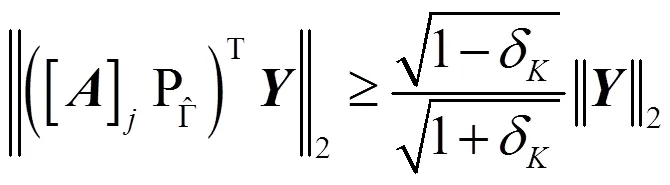
2.2 SAOMP目标定位算法

3 实验及仿真结果分析

图2 SAOMP算法流程示意图

图3 实验场景

图4 目标定位结果

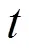
图5 目标跟踪结果

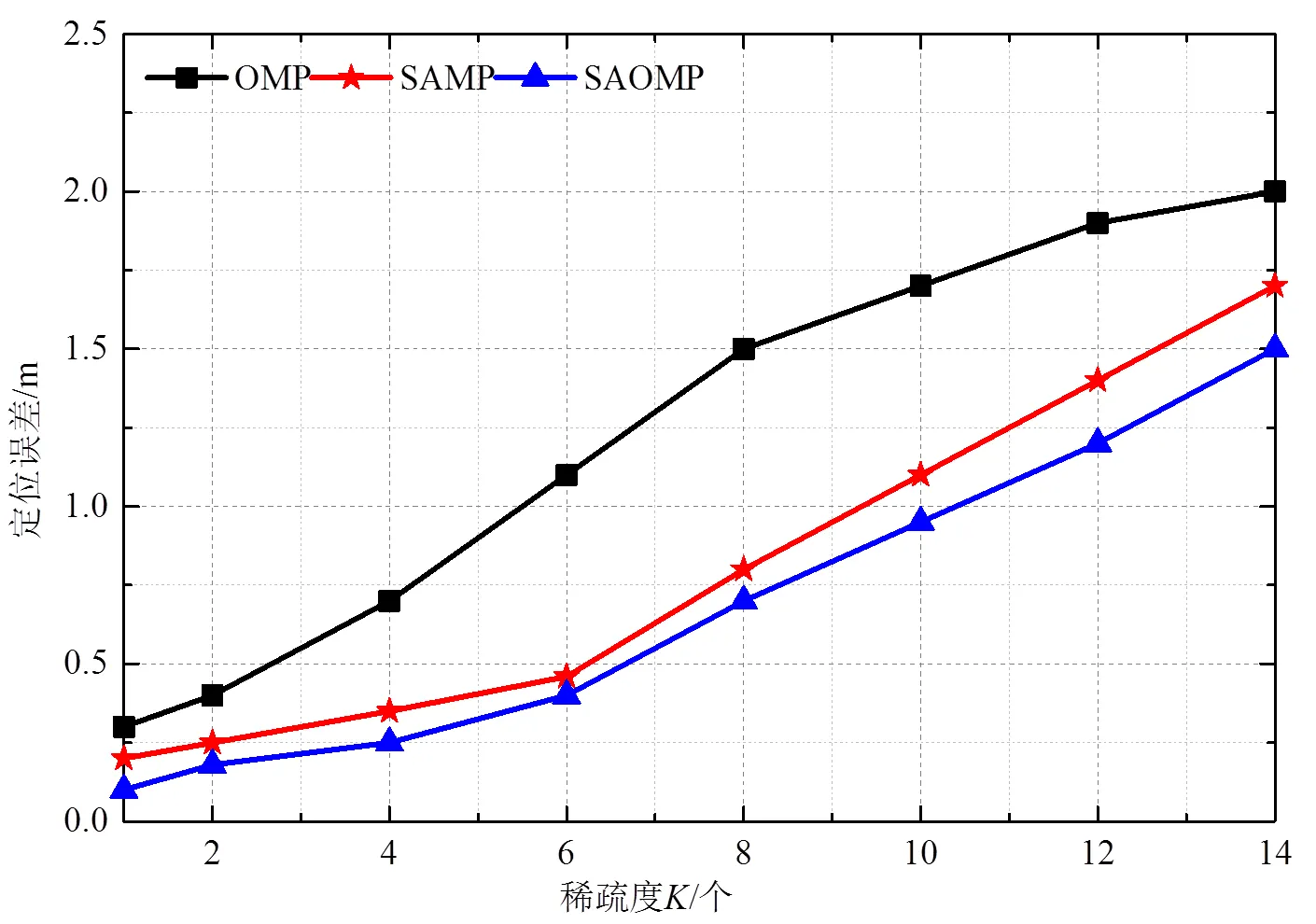
图6 稀疏度对定位性能的影响

图7描绘了链路条数（传感器收发节点组数）对定位性能的影响。由图7中曲线可知，三种定位算法的定位精度均随链路条数的增加而升高，因为随着链路条数的增多采集的数据量就越大，所以必将导致定位精度的提高和运算量的增加。综合上述分析，本实验场景中将通信链路条数设置为7条时为最优的选择，且SAOMP算法能够达到预期的目标定位精度。

图7 链路数目对定位性能的影响

图8 展示了OMP算法、SAMP算法以及SAOMP算法对目标位置估计误差的累积分布函数。OMP算法的位置估算误差较大，主要是由于其不具备自适应稀疏度估算功能造成的。SAMP算法位置估算误差均较小，SAOMP算法的位置估算误差最小，但SAOMP算法的运算复杂度最高。由此可见高精度的定位算法均是以增加运算复杂度为代价，故定位精度和运算量二者不可兼得。综合考虑来看，SAOMP算法的定位性能要优于现存的多种无源目标定位算法。

图8 定位误差的累积分布函数

4 结论

根据CS理论，结合现有的无源目标定位算法研究了如何将多目标的无源定位问题转化为CS理论中信号恢复的问题，提出了一种稀疏度自适应的无源目标定位算法，通过实验把SAOMP算法与传统算法进行了定位性能对比，依据实验结果得出如下结论：

（1）所设计的SAOMP算法能够自适应估算出信号的稀疏度，避免了SAMP算法在估算稀疏度时步长选择的难题。

（2）SAOMP算法的定位精度高于传统定位算法，但运算量较大且运算复杂度较高。

（3）结合文献[10]中的OCKF滤波算法可以实现对目标的精确跟踪。

综合来看，SAOMP算法的可行性和有效性通过实验均得到了验证，而且算法具有较高的估算精度，其定位性能优于现有的无源目标定位算法。

[1] HSIAO R S, KAO C H, CHEN T X,et al. A passive RFID-based location system for personnel and asset monitoring[J]. Technology and health care: official journal of the European society for engineering and medicine, 2018, 26(1):11-16.

[2] YAN L B, LU Y, ZHANG Y R. An improved NLOS identification and mitigation approach for target tracking in wireless sensor networks[J]. IEEE Access, 2017(5):2798-2807.

[3] EWOUT V D B, FRIEDLANDER M P. Probing the pareto frontier for basis pursuit solutions [J]. Siam journal on scientific computing, 2008, 31(2):890-912.

[4] DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE transactions on information theory, 2012, 58(2):1094-1120.

[5] 王勇,王雪, 孙欣尧. 基于稀疏信号重构的无线传感网络目标定位[J].仪器仪表学报,2012,33(2):362-368.

[6] 胡文强,齐向阳.基于分布式压缩感知的双通道SARGMTI[J].国外电子测量技术，2016,35(7):17-22．

[7] 徐志军,苗秀梅,吴鑫辉.基于TDOA测量的多目标P-GMPHD跟踪算法[J].计算机与数字工程,2012,40(9):12-15.

[8] 游康勇,杨立山,郭文彬.无线传感器网络下基于压缩感知的多目标分层贪婪匹配定位[J].自动化学报,2019,45(3):480-489.

[9] Zhang X , Du H , Qiu B , et al. Fast sparsity adaptive multipath matching pursuit for compressed sensing problems[J]. Journal of electronic imaging,2017,26(3):1-9.

[10] 闫雷兵,陆音,张业荣.基于TOA/TDOA的一致性正交容积卡尔曼跟踪算法[J].电子学报,2018(8):1989-1996.

TN99

A

2096–7772(2020)01–0020–08

2019-12-20

国家自然科学基金项目（61271236，61801153）；河南工学院博士科研启动基金项目（KQ1852）

闫雷兵（1980―），男，河南南乐人，讲师，博士，主要从事认知无线电技术及无线定位技术研究。

（责任编辑吕春红）