影响气相爆轰波稳定性边界的通用两步反应模型参数分析

郗雪辰， 王新文， 王克剑， 赵学民

(1.山西警察学院治安系， 山西太原 030401; 2.北京理工大学宇航学院， 北京 100081)

0 引言

对涉爆案件进行现场勘查，是公安机关刑事侦查工作的重要内容之一，利用计算机技术复原爆炸现场，或对现场进行分析研判，可以为涉爆案件的侦破提供有效的帮助；从安全防范的角度来看，对可能发生的爆炸进行风险评估，有助于相关的规范标准和应急预案的制定。为了能够实现计算机技术在公共安全和公安涉爆领域的应用，建立一套可靠的爆炸预测模型就具有重要的实践意义。爆炸发生时，燃料及爆炸物剧烈的化学反应，以燃烧波的形式由点火源开始向外传播。通常根据传播速度将这种自持传播的燃烧波分为爆燃和爆轰。爆轰燃烧是化学反应和气体流动过程的耦合，这种极快速的能量释放，表现出很强的破坏性。因此，对爆轰现象及其传播规律进行研究，也是相关领域的重要课题之一。

早期的研究者提出CJ(Chapman-Jouguet)理论来定量预测爆轰速度，之后又建立了ZND(Zeldovich-von Neumann-Doring)模型描述爆轰波结构,模型假设爆轰波有一个稳定的一维结构，这个结构由前导激波和其后的化学反应区构成[1]。自持传播的一维ZND爆轰是不稳定的，但是通常很难在实验中观察到这一现象[2]。随着计算机技术的发展，可以以高精度和足够的时空分辨率来对非线性带反应的欧拉方程进行积分运算，从而分析爆轰反应区的精细结构。对于一维的平面爆轰波，它显示出与二维、三维数值模拟时相同的振荡性质[3]。这样可以单独研究一维纵向不稳定性，然后推广到更复杂的高维不稳定性研究中。

一维爆轰波的不稳定性仅表现为传播方向的振荡。常用的化学反应模型主要有单步反应模型和基元反应模型。早期的数值模拟主要采用单步反应模型[4-9]。单步反应模型具有较高的计算效率，但是得到的反应区是连续的。真实系统中的反应区通常为一个明显的诱导区和其后跟随的快速放热反应区。Fickett[10]引入了一个简单的代表一步链分支的反应动力学模型研究不稳定一维脉冲爆轰波，通过调整模型可获得两种可能的反应区结构。但是这种化学反应模型很难确定控制不稳定性的关键参数。而基元反应模型虽然可以很好地模拟复杂的化学反应过程，但是受限于现阶段的计算能力和高昂的计算成本，并非研究此类问题的最佳选择。为了兼顾计算效率和计算成本，Short[11]提出了一种三步反应模型，对链分支反应驱动的脉冲爆轰过程的控制参数进行了研究。该模型将化学反应分为链初始反应、链分支反应和链终止反应。链初始反应的Arrhenius反应需要很高的能量，生成低浓度的自由基。紧接着是低活化能的Arrhenius反应，加速自由基的生成。最后是放热的链终止反应。此后，Short和Sharpe[12]将三步反应模型简化成了两步反应模型。该模型包含了一个由Arrhenius速率定律控制的热中性链分支反应诱导区。计算得到的解与三步模型的解定量上相同。Ng[13]在前人的基础上，采用修正后的两步链分支反应模型，通过改变参数来覆盖稳定性边界内稳定性参数χ的范围，研究了一维爆轰的不稳定性。

研究爆轰波的不稳定性，有助于认识其传播规律。可以为爆炸防控技术中涉及的安全防护、隔爆抑爆等问题的研究提供理论依据。目前，基于两步反应模型的气相爆轰波不稳定性研究较少。本文针对一维爆轰波，采用无粘Euler方程和两步诱导- 放热反应模型，固定参数放热量Q和比热比γ，分别调整诱导区活化能EI、反应区活化能ER和反应速率常数kR，计算无衰减单周期振荡模态的临界参数，通过寻找参数间的对应关系，研究影响稳定性边界的两步反应模型参数。研究结果可为将来利用两步反应模型研究多维爆轰波不稳定性的参数选择提供参考。

1 模型介绍

1.1 控制方程

本文的计算忽略粘性项，控制方程采用无量纲形式的一维反应Euler方程组：

(1)

(2)

(3)

假设气体为具有固定比热比的理想气体，总能量和状态方程为：

(4)

(5)

上述参数ρ、u、p、e、q、T分别表示流体的密度、速度、压力、总能量、化学反应放热量和气体温度。化学反应放热量q的表达式为：

q=λQ

(6)

其中λ表示放热反应进程变量。上述所有变量都用波前未燃气体状态参数进行无量纲化：

(7)

其中下角标0表示波前的气体参数。上述方程与化学动力学模型耦合，用来描述爆轰波结构。采用Ng[13]在Short[12]研究基础上修正的两步链分支反应模型，用两个化学速率控制方程模拟化学反应过程。第一步是热中性诱导区或点火过程，反应速率是对温度敏感的Arrhenius形式：

(8)

其中，ξ表示诱导区反应过程的变量；kI表示诱导区化学反应速率常数，kI=-Uvn，Uvn是CJ爆轰波的激波前沿速度；EI表示诱导区活化能；Ts表示气体经过前导激波之后的温度；H(1-ξ)是阶跃函数：

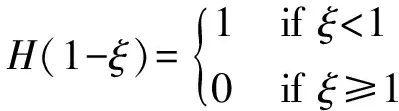
(9)

第二步是缓慢放热之后的快速热量释放过程，其反应速率方程为：

=[1-H(1-ξ)]ρkR(1-λ)exp(-ER/T)

(10)

其中λ表示链重组反应过程变量，kR表示放热区反应速率常数，ER表示放热区活化能。上述公式中的EI和ER都采用RT0进行无量纲化，Ts采用T0进行无量纲化。

1.2 计算模型及参数

本文采用的是色散可控耗散格式(DCD)[14]捕捉激波间断，这是一种基于修正方程的控制而构造的精度高、无振荡的差分格式，属于总变差衰减格式(TVD)中的一种，对流项的差分格式具有空间二阶精度，时间推进采用三阶Runge-Kutta方法。计算域网格尺寸为0.05×0.05，网格数量为40 000×3。所用两步反应模型的主要计算参数包括：放热量Q，比热比γ，诱导区活化能EI，放热区活化能ER，放热反应速率常数kR。其中Q=50，γ=1.2，另外3个参数为可调参数。利用不同的压力振荡模态分析爆轰波的不稳定性，获得两步反应各参数对应的稳定性边界。

2 结果与讨论

2.1 两步反应模型参数与稳定性的关系

研究两步反应模型参数与稳定性的关系，其结果可用于定义稳定性边界两侧的参数特性，有助于将来进行涉爆案件分析研判、防护装备设计等研究时，快速选取合理的参数区间。在单步和两步反应模型中，EI与稳定性的关系是相同的，且单步反应只有一个控制参数，便于讨论，因此采用单步化学反应模型计算一维爆轰波的传播。

2.1.1 诱导区活化能EI与稳定性的关系

通过调整活化能EI获得了几种不同的振荡模态，找到了无衰减单周期振荡模态所对应的临界活化能，并将这种振荡模态定义为稳定性边界；同时，获得的临界还可为之后的计算参数选择提供参考。对于衰减的单周期振荡，被认为是小于该边界的，可判定为一维爆轰传播稳定。对于增长的单周期振荡，以及出现倍周期分叉后的多周期振荡模态，则认为是大于边界的，判定为爆轰传播不稳定。

对于单步化学反应Arrhenius速率模型来说，由活化能EI决定的化学反应的温度敏感性是最重要的稳定性参数。单步反应的Arrhenius方程为：

(11)

其中，A、EI、R和T分别表示指前因子、活化能、混合气体的气体常数和混合气体温度。活化能和指前因子的对应关系如表1所示：

表1 活化能EI和指前因子A的对应关系

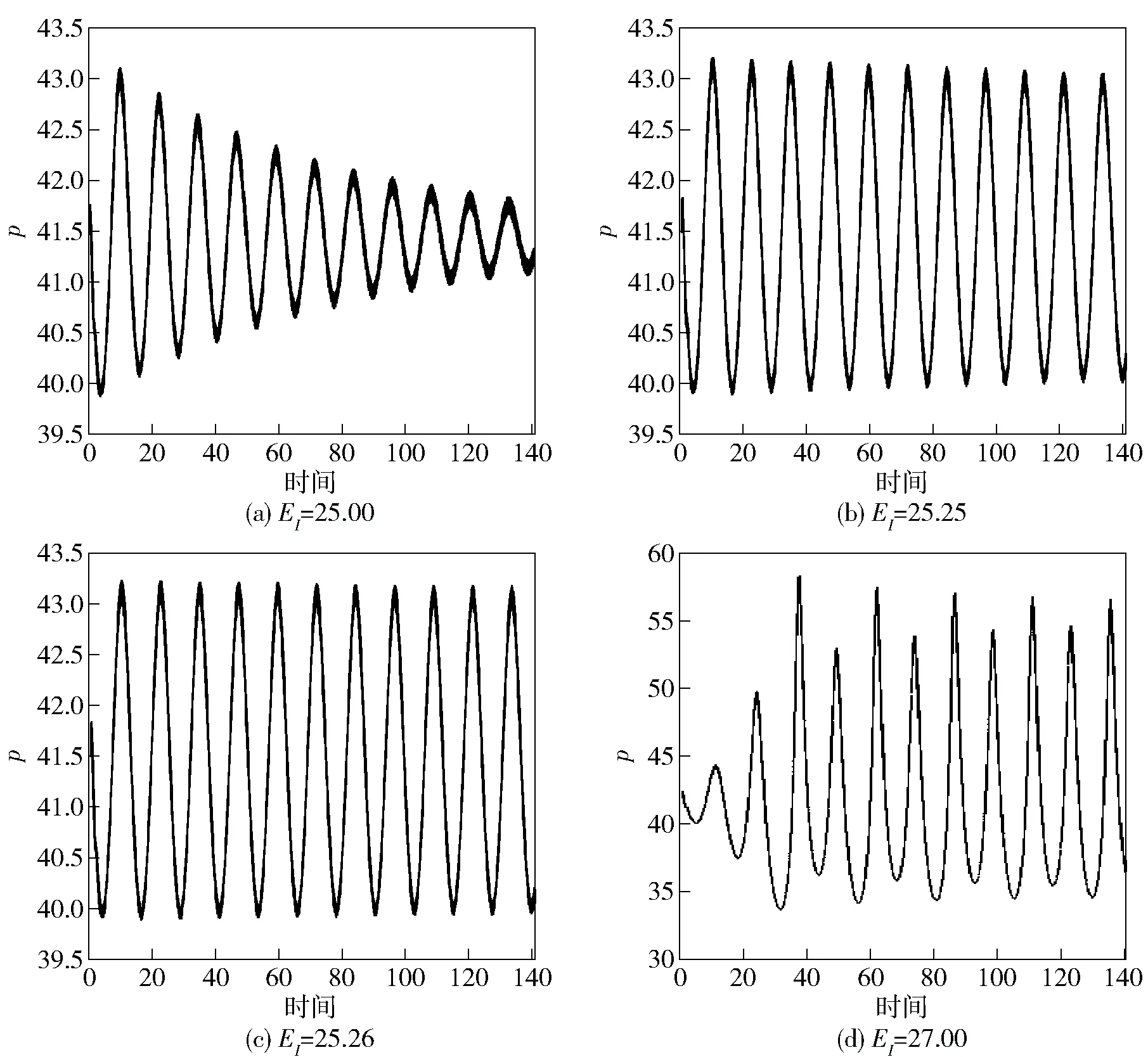
图1 EI分别为25.00，25.25，25.26和27.00的振荡模态

不同活化能的爆轰波振荡模态如图1所示。图1(a)显示的是EI=25.00时的振荡模态，此时呈现为快速衰减的单周期性振荡，而且从时间坐标看，后周期的振幅明显小于其前周期的振幅，这种衰减的单周期波形说明爆轰的传播是趋于稳定的。以前的研究表明，随着活化能EI增大，爆轰的传播会向不稳定状态发展，呈现出不同的振荡模态。为了寻找Q=50，γ=1.2条件下单步反应的稳定性边界，通过缓慢增加活化能，引导爆轰向不稳定状态发展。发现当EI=25.25时，结果表现为临界稳定的单周期振荡模态，即达到了单步反应的稳定性边界，如图1(b)所示。当EI=25.26时就成了无衰减振荡，如图1(c)所示，这表明爆轰波已经开始不稳定。继续增加活化能，发现初始周期振幅几乎不变，周期振幅会随着时间越来越大，使整个波形表现为扩张的单周期振荡。图1(d)为EI=27.00时刻的图形，此时的爆轰波传播已经出现了向双周期振荡转变的现象，且振幅显著增加。当活化能增加到一定值后，单周期振荡会经过倍周期分叉，呈现出双周期、四周期等多周期振荡模态，最终变成混沌状态。显然，高活化能情况下的爆轰是不稳定的，这是由于反应速率对温度的敏感性强，较小的温度扰动就会导致反应速率的大幅波动。

2.1.2 放热区活化能ER与稳定性的关系

与单步化学反应模型不同，两步诱导- 放热反应模型的振荡模态不仅和EI有关，还受到放热区活化能ER和反应速率常数kR的影响。两步反应中的诱导区活化能，采用单步反应模型求解得到的无衰减单周期振荡模态对应的临界活化能EI=25.25。

图2 不同ER的振荡模态

对于给定的反应速率常数，通过调整活化能ER，得到的爆轰波面的压力振荡历程如图2所示。可以看到，爆轰波在最开始会短暂经历计算带来的数值振荡，之后则表现出良好的周期性。图中稳定振荡曲线表示ER取1.0、2.0和3.0时稳定性边界对应的波面振荡模态，此时kR分别为1.32、1.46和1.61。在稳定kR的情况下，增大或减小ER的取值，可以知道两步反应中放热区活化能与爆轰波不稳定性的对应关系。由结果可知，在小ER的情况下，波面的压力振荡表现出振幅逐渐增加的单周期振荡模态，且拥有更大的振幅和更短的波长，这表明一维爆轰波已经跨过稳定性边界向不稳定状态模态发展。增大ER可促进爆轰波向稳定发展，这一结果与Ng的理论相符。

2.1.3 反应速率常数kR与稳定性的关系

给定放热区活化能ER，调整反应速率常数kR，考察其对振荡模态的影响，并寻找各参数条件下稳定性边界对应的临界反应速率常数。图3显示了放热区活化能分别为1.0、2.0和3.0时，几种kR参数的振荡模态，所取ER覆盖了常见燃料的参数区间。由计算结果可以看出，增大kR对爆轰波的失稳过程起到一定的促进作用，诱导振荡模态从单周期向多周期过渡。活化能分别为1.0、2.0和3.0时，稳定性边界对应的kR分别是：1.32、1.46和1.61。从图中可以看出，稳定后的振幅未发生显著变化，但是发现波面振荡的压力区间会随着kR的增大缓慢提高。随着ER的增加，一维爆轰趋于稳定，因此稳定性边界对应的kR也在增大。与活化能不同，反应速率常数kR是两步反应为了便于模型化研究而加入的控制参数。因此该参数并不直接影响爆轰波的不稳定性，只是在一定程度上控制振荡收敛的速率。

图3 不同kR的振荡模态

2.2 两步反应参数对稳定性边界的影响

图4 不同EI对应的稳定性边界

之前讨论了两步反应参数与稳定性边界的关系，同时获得了稳定性边界对应的两步反应参数。对几种EI条件下的放热区参数进行了统计，得到的稳定性边界线如图4所示。该边界线表示了EI分别为15.25、20.25和25.25 3个参数条件下，反应区参数在临近无衰减单周期振荡时的取值变化。可以看出，在稳定性边界上，活化能和反应速率常数呈正相关，这种关系与EI的取值无关。在诱导区活化能EI取值在15.25～20.25的区间内，稳定性边界对kR的变化更加敏感，也就是说在此区间内kR对稳定性的影响占主导。随着EI增大，取值在20.25～25.25区间内，稳定性边界对kR的敏感程度大大降低，充分说明低活化能情况下爆轰非常稳定。低活化能对应的稳定性边界拥有高反应速率，反应速率加快对爆轰波向不稳定发展有促进作用。因此在稳定性边界上，爆轰波在传播方向上的压力振荡非常剧烈，如图5所示。

图5 稳定性边界的振荡模态

以单步反应稳定性边界对应的临界活化能为固定参数，通过调整两步反应中的放热区活化能和反应速率常数，获得了临近无衰减单周期振荡模态的参数对应关系。在此基础上，又分别计算了诱导区活化能15.25和20.25的情况，并获得了这两个活化能条件下的参数对应关系，统计数据如表2所示。

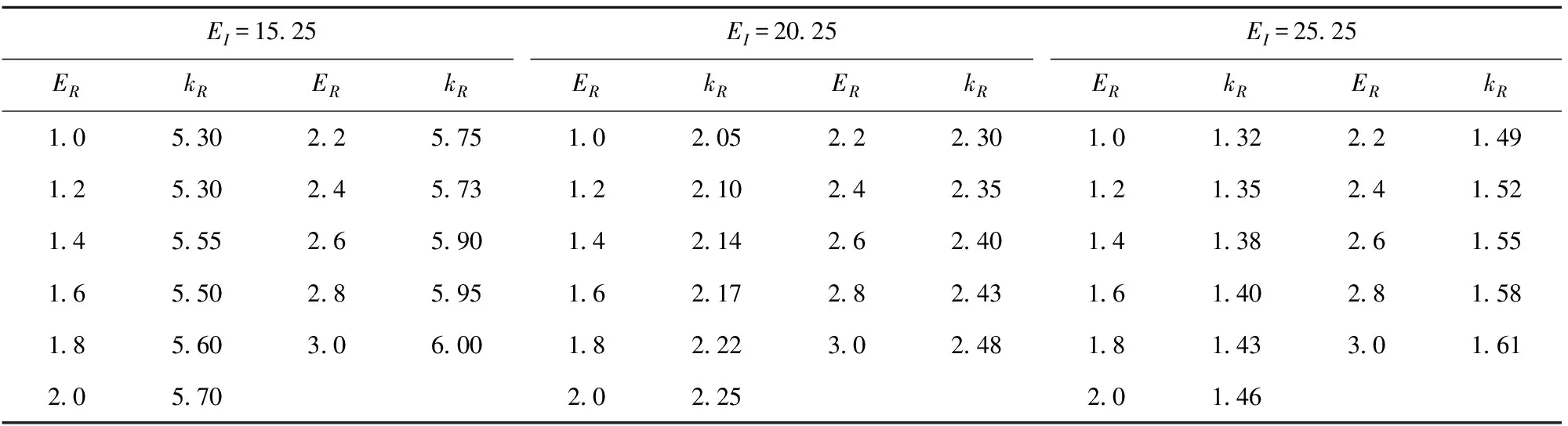
表2 稳定性边界对应的模型参数

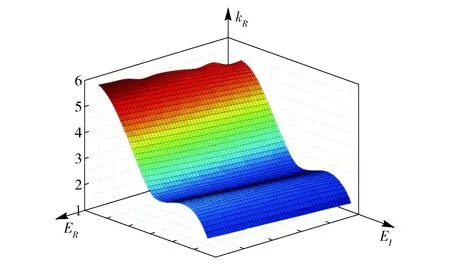
图6 一维爆轰波稳定性边界

为了得到更加直观的稳定性边界，利用Matlab对上述数据进行插值计算，绘制了由两步反应关键参数构造一维爆轰波稳定性边界面，如图6所示。位于边界面以上的参数组合，得到的爆轰波是不稳定的；位于边界面以下的参数组合，爆轰波是稳定的。从图6可以明显看出，活化能增大，稳定性区间就越小。

3 结论

本文采用两步诱导- 放热反应模型，对不同参数条件下的一维爆轰波进行了数值模拟。计算结果显示，增大EI和kR，或减小ER，会促进一维爆轰波跨过稳定性边界，向不稳定状态发展；对于给定的EI，稳定性边界对应的ER和kR呈正相关，即在稳定性边界上，ER越大，kR也越大；在合理的参数范围内，EI越大，ER和kR满足稳定一维爆轰波的取值范围越小；EI在15.25～20.25区间内，稳定性边界对kR的变化比较敏感；EI在20.25～25.25区间内，稳定性边界对kR的敏感程度大大降低。

通过分析各参数与爆轰波面压力振荡模态的关系，寻找无衰减单周期振荡模态对应的临界参数，利用两步反应模型中的几个关键参数，构造了一维爆轰波的稳定性边界。研究获得的稳定性边界，可以作为利用两步反应模型研究多维爆轰波稳定性问题的参数选择依据，属于建立爆炸预测模型的基础性工作。建立的爆炸预测模型，将来可以应用于爆炸现场分析及还原、爆炸物销毁现场方案制定、风险评估、搜排爆防护装备的研发改进，以及隔爆抑爆技术研究等领域。