基于时间权重和用户兴趣变化的协同过滤算法

王娜娜

(安徽理工大学 计算机科学与工程学院，安徽 淮南 232001)

互联网和信息技术的普及，使人们进入信息化时代。然而，近几年资源迷向、信息过载等现象日益严重。因此，为人们提供便利的推荐系统应运而生。在社交网络、电子商务、电影、音乐、个性化邮件以及阅读等领域应用广泛。推荐系统是一种信息过滤手段，其能有效根据用户的需求，快速、准确地为用户推荐有用资源。

目前，推荐系统由三类构成，分别为基于内容的、协同过滤的和混合的推荐。而基于协同过滤的推荐是最常用的个性化推荐技术。随着推荐系统中用户和项目的数量日益庞大，用户冷启动、数据稀疏性、可扩展性等问题逐渐增多，而传统的协同过滤算法在进行个性化推荐过程中通过用户—项目评分矩阵计算项目相似度或用户相似度，未考虑项目类型和时间距离这两个因素给用户兴趣变化带来的影响。

基于此，本文提出了一种基于时间权重和用户兴趣变化的协同过滤方法TACF(time and interests collaborative filtering)。首先，通过构建的用户兴趣分布矩阵，得到用户兴趣分布向量，并采用修正的余弦相似度计算用户间存在的兴趣相似度；然后，引入时间权重函数，计算基于时间权重的用户评分相似度；最后，将两种相似度进行线性加权，找出与目标用户最相似的k个邻居并且预测未评分项目的评分值，产生Top-N推荐。流程图主要分为3部分，具体挖掘流程如图1所示。

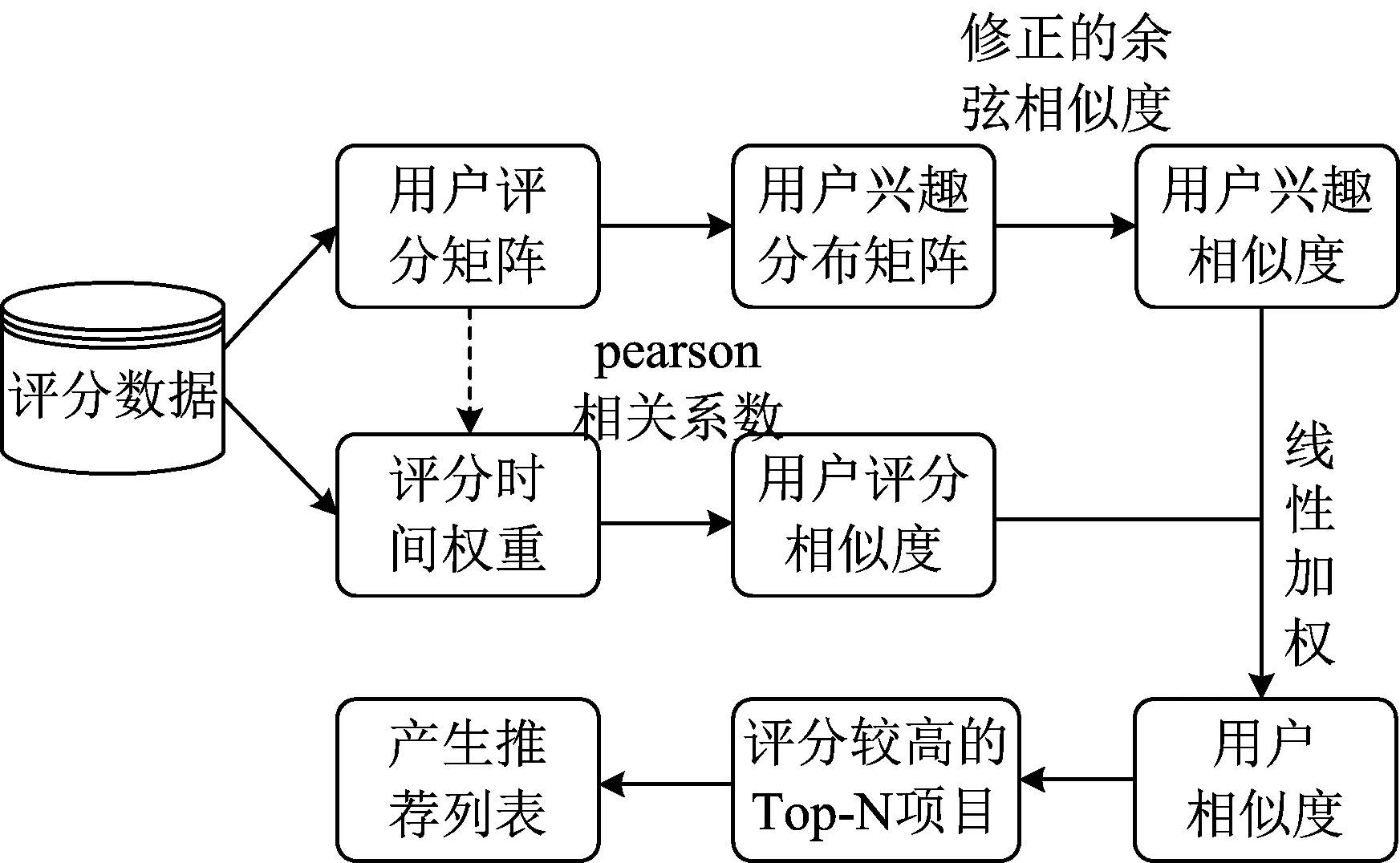
图1 ATCF算法流程图

1 相关工作

目前，随着推荐系统中用户和项目数量的急剧增长，在推荐系统应用中，国内外常采用的方法主要分为三类。

1)基于内容的推荐算法是从用户信息中挖掘其潜在的兴趣点；然后，把预推荐内容与挖掘出的兴趣点进行相似度比较和分析，最后，将相似度高的内容推荐给用户。张桂平等人针对单一角度描述用户兴趣不全面，提出一种基于用户行为和用户主题兴趣的文档推荐方法[1]。Sedhain等人在协同过滤算法中引入人口统计学数据和社交信息，避免冷启动问题[2]。李伟霖等人通过从用户评论文本中提取用户观点，来修正协同过滤推荐算法[3]。蒋胜等人根据动态社会行为和用户背景信息，有效解决冷启动和数据稀疏问题[4]。

2)协同过滤推荐可细分为基于项目和基于用户的推荐，主要是根据相似的思想为用户进行推荐。范洪博等人针对无法对用户进行多兴趣话题推荐，提出融合用户背景和用户人格信息的话题推荐方法[5]。徐蕾等人在协同过滤系统中的应用博弈论的方法对用户评分行为进行分析，提出了基于均衡学习的算法[6]。李豪等人考虑项目属性的不同是否会对用户兴趣变化产生影响，引入“兴趣分布矩阵”，并设计启发式评分方法[7]。Hernando等人通过采用用户评分矩阵进行分解的方式对用户兴趣进行分析[8]。Patra等人通过结合Bhattacharyya系数的相似度计算方法，有效改善数据稀疏问题[9]。

3)基于混合的推荐算法是通过组合不同类型的算法，达到能够在充分利用各自算法优点的同时克服各自缺点的目的。杨武等人将基于内容和基于协同过滤的推荐算法组合进行新闻推荐，虽然能有效缓解数据稀疏性问题，但是该方法应用范围有限[10]。赵文涛等人提出基于用户多属性和用户兴趣结合的方法，有效改善数据稀疏性和冷启动问题[11]。Park等人提出一种K近邻图的快速协同过滤算法，该方法不仅能提高推荐准确率，还能提高计算速度[12]。张玉连等人提出在融合用户相似度和项目相似度的加权方法改进Slope one算法[13]。董晨露等人将遗忘曲线和用户评论引入协同过滤算法中，该算法能在稀疏数据集上获得较好的推荐结果[14]。

综上所述，上述研究均在其提出方法的基础上提升了推荐系统的推荐质量。但大部分学者研究范围主要围绕用户属性、项目评分等基本信息，鲜有学者考虑项目类型和时间变化给用户兴趣波动带来的影响。因此，本文提出的TACF算法，主要是通过构建用户兴趣分布矩阵和引入时间权重函数改进协同过滤算法，实验表明该方法能为目标用户提供更加准确的个性化推荐。

2 基于TACF算法设计

2.1 用户—评分矩阵的建立

假设推荐系统中存在m个用U={u1,u2,u3,…,um}和n个项目I={i1,i2,i3,…,in}。用户—项目评分矩阵Rmn={Rui}，用户u对项目i的评分可表示为Rui。如下表所示。

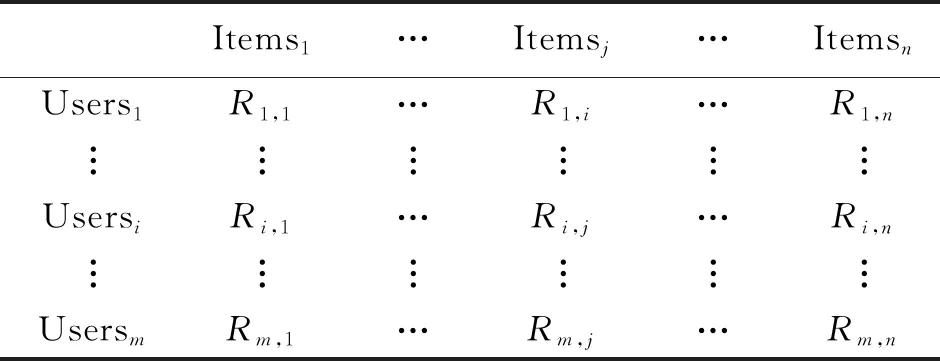
表1 用户—评分矩阵Rmn

2.2 用户兴趣相似度计算

2.2.1 用户兴趣变化分析

由于传统推荐算法大多根据用户对项目的评分值多少，根据相似度公式计算用户与用户间的相似度，忽略项目类型属性对用户兴趣变化带来的影响。而项目本身通常具有明显的类别属性，例如音乐项目具有“乡村”“流行”“古典”等属性，电影项目具有“爱情”“喜剧”“科幻”等属性。这些项目本身具有的属性在一定程度上会影响用户的评分，间接反映出用户的兴趣分布。

因为用户的兴趣爱好各不相同，所以通过历史行为来挖掘用户在某个属性上的是否存在兴趣。历史行为可以分为用户对该类型项目的打分情况和标记该类型项目的数量。例如在电影项目中，若某用户共标记了280部电影，其中有190部为“喜剧”电影，25部为“科幻”电影，从评分数据中看出喜剧评分为3.6，科幻评分为8.0。直观地考虑，该用户对喜剧更感兴趣，因为观看喜剧数量较多。但是从打分情况考虑，用户更满意科幻电影。出现这种情况的常见原因可以理解为用户虽然观看数量少，但是其观看的科幻电影均为口碑较好的电影，从打分情况看出用户满意度很高。因此，一个个性化推荐系统不仅要推荐用户明显感兴趣的项目外，还要根据历史信息挖掘其潜在兴趣，上述情况喜剧和科幻项目类型均应该列入推荐列表，即评分和标记数量均是反映用户兴趣的重要因素。

2.2.2 用户兴趣分布矩阵构建

假设系统中项目本身的固有类型有C个，Mi表示项目ji的类型向量，用Mi={m1,m2,m3,…,mn}表示项目类型向量集合，mn取值为0或1，其中0表示项目不存在此类型，1表示存在此类型。由于一个项目可以存在多个类型，则所有项目的类型矩阵表示为矩阵M=[M1M2M3…Mk]T

Ei=[Ei,1Ei,2Ei,3…Ei,c]

则所有用户的兴趣分布矩阵构建为：

E=[E1E2E3…Ek]T

将用户—评分矩阵R中不为零的值全部设置为1，即可得到用户—标记项目矩阵S。用户标记项目在C个类型上标记数量分布矩阵表示为Q，则:

Q=S×M

(1)

那么，用户标记的项目在C个类型上的平均评价表示为矩阵H，则：

(2)

由于矩阵中不存在除法运算，公式(2)中分子分母均为n×c矩阵，公式中的除法表示分子分母中对应位置相除。

为了能使用户间的比较更加方便，本文对矩阵Q、矩阵H中的每行向量进行归一化处理，其公式如下：

(3)

进行归一化处理后的矩阵分别记为Q′和H′，其中，矩阵Q′表示用户兴趣在C个类型上的标记数量分布，矩阵H′表示用户兴趣在C个类型上的用户评价分布，进而得到用户兴趣分布矩阵计算公式为：

E=α×Q′+(1-α)×H′

(4)

其中α为可变参数，取值范围为0～1，参数取值会通过多次实验模拟选取使推荐结果最优的值。

2.2.3 用户间的兴趣相似度计算

本文采用修正的余弦相似度计算用户间的兴趣相似度sim1(u,v)，具体计算公式如下：

走在路上看到的场景、幼儿园发生的冲突、动画片里看到的故事，我总是时不时这么问她，然后和她讨论思考。有的问题孩子无法回答，我就会告诉她；有的问题她有了自己一定的答案，我也会顺势引导。

(5)

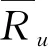
2.3 基于时间权重的用户评分相似度

2.3.1 用户评分时间权重计算

在推荐系统中，时间信息是非常重要的一种信息[15]，其对用户的个人兴趣也产生了较大的影响。用户的兴趣和行为会随时间的变化而变化。例如程序员用户在工作初期比较倾向于选择阅读入门类的书籍，但随着工作时间的积累，逐渐从入门类转变为专业类书籍；另外，用户对项目的行为还会受到季节效应的影响，例如用户在不同的季节对不同的衣服兴趣度不同。通常，我们会认为用户最近访问的项目就为其感兴趣的项目。因此，本文引入时间权重公式计算其对用户评分的影响。

(6)

其中，t取值范围为[0-1]，w(tu,i)取值范围为(0-1)。由公式知，w(tu,i)函数是一个单调递增函数，其值随时间t增加而增加，但不会超过1；tu,i表示在时刻t时用户u对项目i的评分值。实验前，本文通过标准公式将用户评分的时间变量转化为[0,1]。其中，时间变量的变化可以直观的从权重上看出，可以通过权重大小精确地分析用户兴趣的变化，进而达到为用户提供更加准确的个性化推荐的目的。

2.3.2 用户评分相似度计算

本文采用pearson相关系数计算相似度的方法来计算用户评分相似度sim2(u,v)，具体计算公式如下：

(7)

其中，sim2(u,v)表示用户u和v之间基于时间权重的用户评分相似度；w(tu,i)表示用户u对项目i评分的时间权重。

3 基于组合相似度的推荐

3.1 用户总相似度计算

组合基于用户兴趣和基于时间权重的相似度，通过计算得到用户总相似度，使用线性加权方法进行组合，具体公式如下：

sim(u,v)=λsim1(u,v)+(1-λ)sim2(u,v)

(8)

其中，γ、1-γ分别表示sim1(u,v)和sim2(u,v)相似度权重，且γ取值为[0-1]，在本文中由于两种相似度方法占据比例相同，本文γ取值为0.5。

3.2 改进的评分公式

计算用户总相似度，选取前k个最近邻居，得到最近邻居集合后，对目标用户进行项目推荐。在推荐系统中，用户影响力是影响推荐结果的重要因素之一，人们更倾向于采纳经验丰富的人提出观点。例如一位观影量超过3000部的用户提出的观点与普通用户观点更具有权威性，即在进行推荐时，应该首先被考虑。因此，改进的评分预测公式如下：

(9)

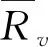
3.3TACF 算法描述

通过上述讨论，本文设计了一个简洁的算法来帮助理解如何进行个性化推荐。

算法：TACF算法设计

输入：用户-评分数据

输出：推荐列表

1:输入用户-评分矩阵

2: do

3: {

4: for(矩阵不为空)

5: {对用户进行聚类，再根据公式(1)～(4)计算用户兴趣分布矩阵}

6: end if

7: for(根据兴趣分布向量)

8: {根据公式(5)计算用户间的兴趣相似度}

9: end if

10： for(矩阵不为空)

11： {根据公式(6) ～(7)计算基于时间权重的评分相似度}

12: end if

13: for(矩阵不为空)

14: {根据公式(8)计算基于两者线性组合的总相似度，根据公式(9)进行评分预测，产生推荐列表}

15: }

16: end

算法设计说明：

1)第一个判断，即step2-step6，判断用户—评分矩阵是否为空，若不为空则进行下一步操作反之则终止。

2)第二个判断，即step7-step9，根据构建的用户兴趣矩阵，得到用户兴趣分布向量，计算用户间的兴趣相似度。

3)第三个判断，即step10-step12, 根据构建的用户-评分矩阵计算基于时间权重的评分相似度。

4)第四个判断，即step13-step16,采用线性加权的方法计算总的相似度，并使用改进的评分公式进行评分预测。

4 实验结果与分析

4.1 实验数据

本次实验采用网上开源的MovieLens站点提供的100 K数据集，通过943对用户根据1682个电影项目打分产生的10万条评分数据，计算得数据稀疏度约为94%，且每队用户评分电影数量不少于20部。评分等级分为1分至5分，分值越高表示用户对该部电影兴趣度越高。将实验数据平均分为五组，采用随机法选取其中一组作为训练集，剩下的四组作为测试集。

4.2 评价指标

选择平均绝对误差(MAE)作为本次实验的评价指标。表示系统预测评分与真实评分之间的误差，以此衡量算法推荐的准确度。

(10)

其中，rui、r′ui分别表示用户对项目的实际评分值和推荐算法计算出的预测评分值；n表示测试集中的项目个数。

4.3 实验结果

为使推荐算法能在最优参数下对用户进行推荐，最重要的一点就是确定参数值。在α分别取0.1至0.9的情况下，测试TACF算法在不同α值下的MAE值。

从图2可以看出，随着α值得不断增大，MAE值呈现波动，当α为0.5时，MAE值取得最小值，即此时算法的推荐质量最高，具体数据如下所示。

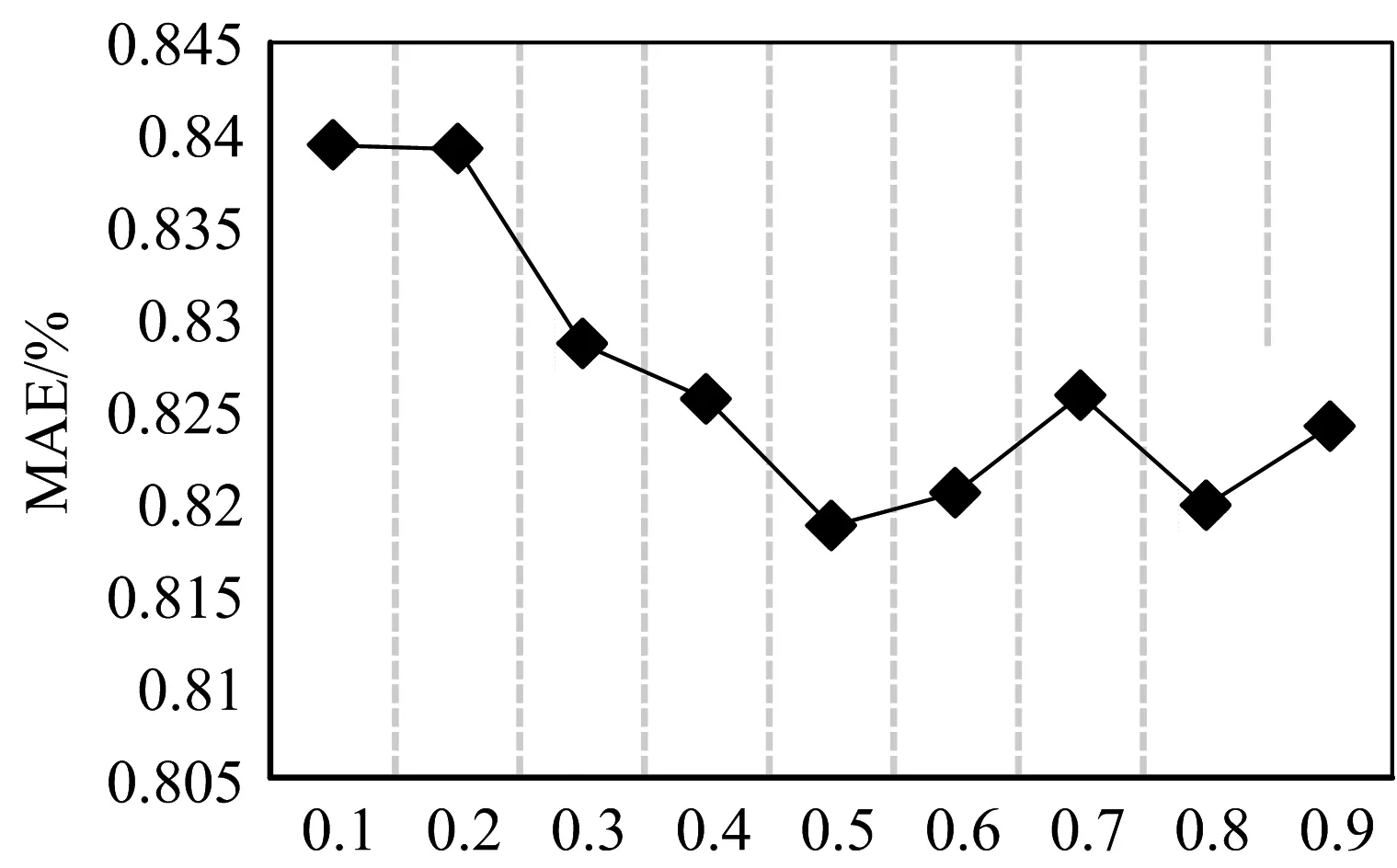
图2 TACF算法在不同α值下的MAE值

为验证本文提出算法的推荐准确率，将本文提出的算法(TACF)和基于物品的(IBCF)以及基于用户的(UBCF)推荐算法在不同K最近邻数量的情况下进行对比分析，实验数据如下所示。

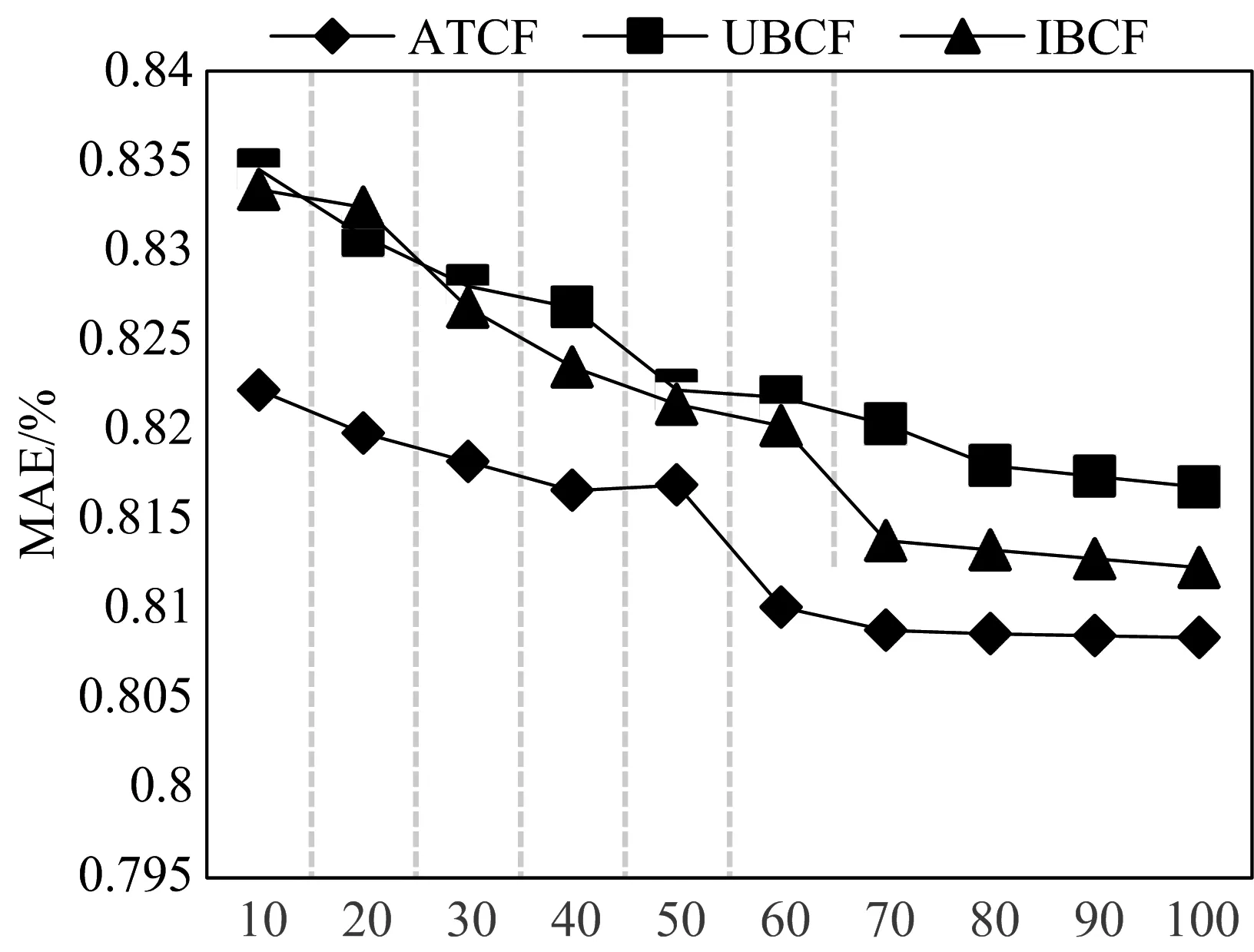
图3 不同算法的MAE值对比

从图3看出，随着K值得不断增大，三种方法的MAE值逐渐减小，即算法预测结果更加准确，但是在真实测试数据中，由于存在用户冷启动、数据稀疏性等问题，从图中可以直观地看出K增加到一定数值时，MAE值逐渐趋于稳定，即准确度提升程度减缓甚至有下降趋势。当K为70时，MAE值趋于稳定且明显低于UBCF方法和IBCF方法。实验表明，本文方法可以显著提高推荐准确率，并为用户提供更加令人满意的个性化推荐列表。

5 总结

本文在传统推荐算法中增加了用户兴趣分布矩阵以及基于时间的权重函数，能够有效解决用户—评分矩阵数据稀疏性和推荐准确度低等问题。计算用户间的兴趣相似度时，本文通过挖掘用户历史数据对评价过的项目类型进行分类，研究项目类型对用户兴趣度的反映；另外，在用户评价过程中，提出基于时间权重的用户评分相似度计算，根据评价时间的先后，可以判断用户近期兴趣变化趋势；本文将两者进行线性加权，在相似度计算过程中，通过动态调整两者所占比例，使相似度组合达到最优。最终寻找出与目标用户最相似的前K个最近邻进行评分预测，进而使用Top-N算法产生推荐列表。本次实验结果显示，本文提出的推荐算法能够有效提高用户间的相似度，显著提高推荐准确度，在数据稀疏的情况下，能较好地提高推荐质量。下一步可以尝试在TACF算法的基础上融入用户多属性分析，从而达到更高的推荐精确度。