地域分散化投资策略研究——以中国股票市场为例

司徒健彬，潘 强，陈洁容,3

(1.珠海城市职业技术学院，广东 珠海 519090；2.暨南大学珠海校区，广东 珠海 519070；3.澳门科技大学，澳门 氹仔 999078)

对投资者而言，投资的目标就是最大化投资收益以及最小化投资风险。经典资产组合理论认为，投资者在进行投资决策时应当进行分散化，从而达到提高投资组合收益或者降低投资组合风险的目标，甚至投资者可以持有分散化市场组合以获得最优市场回报(Markowitz，1952)[1]。资本资产定价模型(CAPM)假设所有的股票都承担了系统性风险，而分散化资产组合则能够减低非系统风险(Lintner,1965)[2]。

施东晖(1996)[3]发现中国上海的股票市场上随机选择一种股票的收益率方差为4.18%，20 支股票组成的资产组合则能够将收益率方差降低至接近3.28%的水平，分散化投资可以降低大约20%的非系统风险。吴世农和韦绍永(1998)[4]以等权组合的方法研究了一种股票至30 种股票的不同组合，发现在中国上海股票市场中，资产组合风险随组合规模增大而下降。当股票数量从一种增加至五种时，组合风险得到显着分散。随着股票数量的增加，扩大资产规模以降低风险的程度逐渐下降，当组合中股票数量由21 种增至30 种时，组合风险几乎不再减少。总体而言，通过分散化组合，投资者可以降低大约25%的风险。李善民和徐沛(2000)[5]验证了中国上海和深圳市场组合规模与风险的关系，并建议投资者持有的股票大约可以控制在20 种以内，适度的资产规模可以使总风险下降约50%。姜茂生、张雪丽(2001)[6]通过随机选股的方法构造了包含不同数目股票的投资组合，并计算出投资组合的收益及风险。投资组合股票数目达到五支时，已可以消除90%以上的非系统风险。刘晓彤（2012）[7]验证了投资组合分散化在中国股票市场的有效性，尤其是股票组合数量在五种以内时，风险降低的作用尤为显着。而当分散化组合的股票数量超过10 种时，非系统风险占比的下降速度将明显减少。当股票数量过多时可能会产生一些“负效应”，比如延迟决策、增加研究成本和增加交易成本。

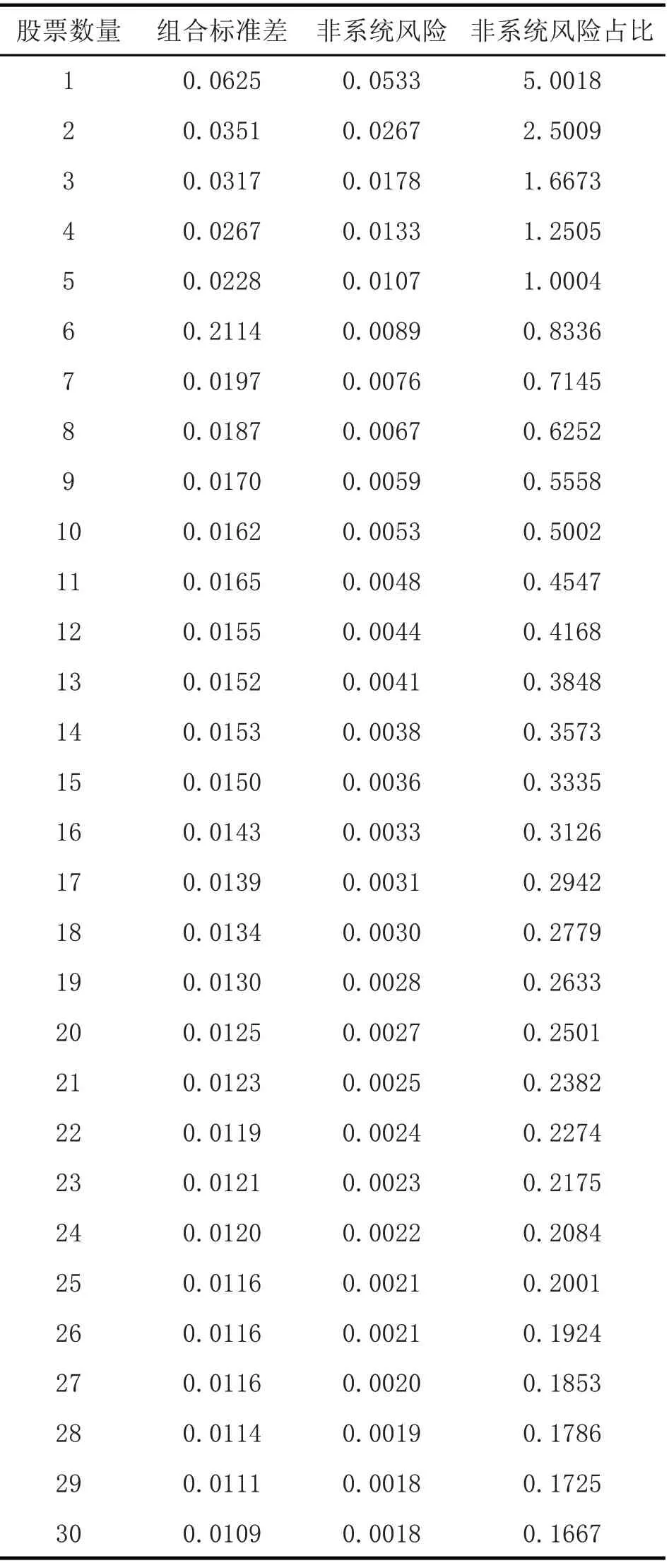
表1 资产组合股票数量与风险的关系

尽管分散化投资对风险降低的作用在中国得到了证实，实际上大多数投资者，尤其是个人投资者并未持有分散化的组合。个人投资者一般被认为是非理性的，在进行复杂的选择时，往往会受自身能力和心理情绪的影响。李延喜、高锐、杜瑞(2010)[8]发现上海、天津和大连的投资者均没有充分进行投资分散化，而是过度投资于本地公司。吴立广和黄珍(2012)[9]的研究表明中国QDII 基金持有的资产组合与基金可能获得的分散化最优组合差距甚远，这些基金均过度投资于地理位置最接近的香港股票市场。

本文的目的是探讨中国投资者可能从地域分散化的投资中所能获得的优势，以Markowitz的理论框架进行了分析，填补中国市场甚至新兴市场在地域投资策略方面研究的空缺。

一、文献综述

过往研究强调资产配置对于投资者来说是最重要的决策，尤其对于基金投资者而言。Markowitz(1952)[1]为投资者提供了一种有效的方式进行风险资产配置：投资分散化。这种分散化投资方式能在多大程度上降低投资风险，取决于风险资产收益率之间的相关性程度。如果资产收益率相关程度较低，分散化投资可以降低更多风险，而资产收益之间相关度较高，则分散化投资的好处将会减少。资产组合的期望收益和收益标准差的计算公式为：

其中，

wi为资产i 在投资组合中所占比例，

E(Ri)为资产i 的期望收益，

E(Rp)为资产组合的期望收益。

公式(1)显示资产组合的收益率即为单个资产收益率的加权平均数，而单个资产的权重则是其在资产组合总值中所占的比例。

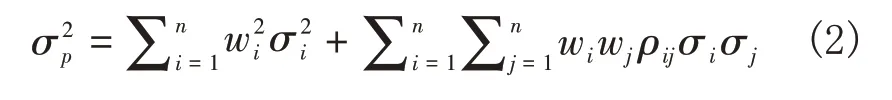
其中，

σp为资产组合的标准差，

wi,wj为单个资产占资产组合价值的比重，

σi,σj为资产i 和j 的收益率标准差，

ρij为资产i 和j 的收益率的相关系数。

公式(2)显示资产组合收益的方差则是单个资产收益方差的加权平均(权重为平方项)，以及单个资产之间协方差的加权平均。资产组合收益率的方差不仅包含单个资产收益率的方差，还包含了单个资产收益率之间的协方差。当资产组合包含了大量相关性低的证券时，资产组合的风险将随着加权协方差的减少而下降。

大多数情况下，投资者本质上都是风险规避的，当两只股票有相同的收益率时，他们将选择风险较低的股票。当多只股票按照不同比例构建投资组合时，就可以产生一系列的收益-方差组合，这些组合的最优解将构成有效边界。有效边界描绘出每一特定风险下能获得的最高收益率，或是每一特定收益率下需承担的最小风险。

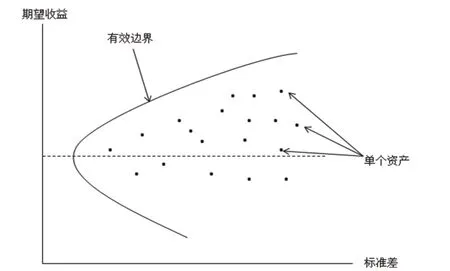
图1 资产组合的有效边界

通过分散化，投资者可以消除投资组合中的非系统风险，但仍然受到系统风险的影响。由于不同区域之间的系统风险因素相关程度低，投资者可以通过分散投资不同区域的资产以降低投资组合承受的系统风险。如果投资者在全球范围进行分散化，则其投资组合只受到世界系统风险的影响。

图2 分散化资产组合的风险

Levy & Sarnat(1970)[10]对28 个国家的资产进行了估计，美国资产有着高的收益率(12.1%)和较低的风险(12.1%)，但美国投资者仍然可以通过国际分散化获得好处。各国资产收益率的相关系数并不高，低相关性的资产正是构建分散化组合的理想因素。Lessard(1973)[11]的研究验证了国际分散化的投资策略在发展中国家的可行性，指出拉丁美洲国家资产收益的因素也是相互独立的，拉丁美洲国家投资者能够从国际分散化投资中获益。与美国资产相比，以拉丁美洲四国构建的分散化市场组合也略占优势。Novack(1977)[12]发现与单一国家资产组合比较，随机配置的分散化组合可以在提高收益率的同时降低风险。Eun & Resnick(1994)[13]发现通过持有最优国际化资产组合，美国投资者能够显着地提高投资收益，并降低投资风险，日本投资者则在降低风险的同时也付出了收益率下降的代价，美国的投资者比日本投资者获益更大。吴立广、黄珍(2012)[9]对中国八只QDII(合格境内机构投资者)基金的资产组合进行研究，指出QDII 基金并未投资于能够达到的分散化有效边界，且距离有效边界偏差较大，八只QDII 基金均过度集中投资香港股票。

按照理性人的假设，投资者应该在投资决策中采取分散化的投资策略。由于中国投资者无法直接投资于国外股票，因此多国分散化的投资对大多数中国投资者来说并不可行。而过往研究鲜有对中国股票市场的省份分散化投资策略进行分析，若多省分散化能够有改善投资绩效的作用，则投资者应当在投资决策中采用分散化的投资策略。

二、数据来源

本研究的数据来源于CSMAR 数据库，以上海市场A 股作为研究样本，月度收益率数据为股票收益超出无风险收益的部分，样本期间从1991 年1 月至2017 年12 月，无风险收益则以一年期定期存款计算。

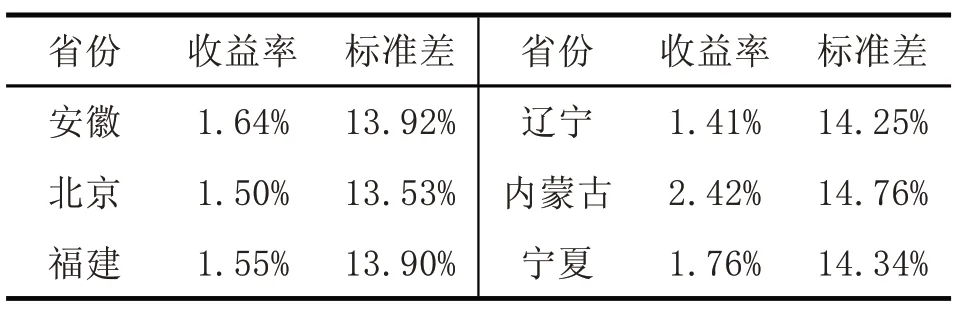
表2 中国31 省股票月度平均收益及标准差，1991-2017

甘肃广东广西贵州海南河北河南黑龙江湖北湖南吉林江苏1.67%1.71%1.51%1.85%1.72%2.10%1.33%1.30%1.54%1.53%1.38%1.51%13.92%14.17%14.52%14.50%17.94%15.99%13.04%17.34%14.27%14.69%13.95%13.72%青海山东山西陕西上海四川天津西藏新疆云南浙江1.20%1.62%1.94%1.19%1.96%1.64%1.68%1.58%1.71%1.46%1.56%15.37%14.36%14.92%14.49%18.04%16.06%14.64%14.81%14.33%14.70%13.61%

表2 显示了中国市场31 个省的股票月度平均收益，平均月度股票收益率最高的是内蒙古，为2.42%，最低的则是陕西，为1.19%。不同省份的月度差距并不明显，大部分省份股票月度收益低于2%，仅内蒙古和河北两省的股票收益率在2%以上。标准差的范围从最高的上海18.04%到最低的河南13.04%，而各省股票收益的波动性相差并不大，25 个省份的股票收益标准差位于13%至15%之间，只有海南、河北、黑龙江、青海、上海和四川的标准差在15%以上。

三、研究设计

为了解多省分散化投资在中国市场能否起到积极作用，本文比较了多省分散的投资组合与单一省份投资组合的表现。本文从各省的上市公司中随机选出了股票代码排行最前的30 家公司的股票构建投资组合，如果一个省拥有在上海交易所的上市公司少于30 家，则以其全部公司股票构建投资组合(其中安徽、辽宁29 家，新疆、陕西21 家)。而分散化的投资组合则从各省的股票中随机选出共30 支，这些省份来自中国不同经济地区。

尽管部分省份的股票能够获得比其他省份更高的收益和更低的标准差，中国投资者仍然可以从分散化投资中获益。资产组合理论(Markowitz,1952[1])证明了只要不同省份的投资收益并不是高度相关，在资产组合中加入收益率较低而标准差较高的省份的股票，仍有可能显著地降低资产组合的整体风险。

由于股票收益率可从历史交易数据获得，要构建股票组合的有效边界就是需要计算出各股票合适的投资比例，使在任意水平的收益率上，其标准差或方差为最低。

而要构建有效边界的方法则是需要找到适合的各股票投资比例wi，使投资组合的标准差最小。由于在中国市场中存在着相应的交易规则，因此投资者对任一股票的投资比例wi需要服从一定的限制：

(1)wi>= 0；

(2)wi<= 1；

由于中国市场对于卖空机制的限制，投资者不倾向在不持有股票的情况下借入股票卖出，对任一股票的投资比例需要不低于零，即限制条件(1)；中国市场对于保证金买入的方式也有所限制，中国投资者的观念也相对保守，对任一股票的投资比例需要不高于100%，即限制条件(2)；限制条件(3)则保证了投资组合中全部股票的投资比例总和为100%。

本研究使用了Excel 中的规划求解(Solver)计算出任意特定收益率水平的最优投资比例，即在特定收益率水平时标准差最小的投资组合，并利用这些收益-标准差组合建立起各省以及多省分散化组合的有效边界，以对比单一省份投资组合与多省分散化投资组合的表现，验证多省分散化对于提高投资表现的作用。在本研究中，每一省份的有效边界由该省的三个投资组合联接而成，包括方差最小组合、Sharpe 比率最大组合以及收益率最高组合。

四、研究结果

通过对比单独以各省股票构建的投资组合以及分散化投资组合的收益-风险水平，可以得知中国投资者在地区分散化中是否可以改善资产组合的表现。为更清晰地阐述各省股票组合的有效边界，本研究首先比较了投资组合中的两种资产组合方式的收益-标准差水平，包括标准差最小的资产组合以及Sharpe 比率(计算方法为资产组合超额收益与标准差之比)最大的资产组合。表3 列出了样本中各省投资组合的月度平均收益-标准差数据。

表3 按不同股票比例构建的各省资产组合收益率与标准差

在各省的最小风险组合上，浙江省的投资组合的表现比其他省的投资组合表现更优，能获得最高的2.45%的月度超额收益，并且其标准差也是最低的4%；与平均比例配置的组合结论一致，陕西的股票组合仅能平均产生0.16%的月度超额收益，为所有省份最低，标准差也仅高于浙江和江苏两省，为6.4%。除浙江外的其他省份收益率均低于2%，而全部省份的投资组合标准差均低于10%，其中标准差最高为新疆的9.64%。

资产组合理论认为最优的组合为Sharpe 比率最高的投资组合，因为这种投资组合收益-风险比最高。即使是将范围局限在同一省份，理性的投资者应该持有这样的股票组合。各省的Sharpe 比率最高组合收益率均位于2%至3%之间，最高为广东的2.99%，其次为最低则是辽宁的2.11%；而在风险水平方面，安徽省的股票组合有最高的标准差11.13%，而浙江省的股票组合标准差最低，仅为4.29%，第二低的江苏省股票组合标准差则上升至8.12%。

表4 显示了本研究选取的13 个省份的股票月度平均收益率的相关性。各省的股票收益相关性程度总体并不高，大部分的相关系数低于0.30，而相当比例的省份股票收益甚至为负相关。由于不同省份的股票之间存在低相关性，投资者可以通过分散投资于多个省份，构建出比投资于单个省份更优的资产组合。在各省的最优资产组合，广东省的股票能获得最高的月度平均收益 (2.99%)，以及中等水平的标准差(9.81%)，而其与部分省份股票收益负相关。即使广东省股票收益的标准差并不低，由于与其他省份股票收益的负协方差，将广东省股票纳入投资组合中即可以降低投资组合的整体风险。同样，浙江省的股票能产生较高的投资收益率(2.74%)和最低的标准差(4.29%)，并且与多个省份股票收益存在负相关，尤其是浙江与广东的股票收益之间相关系数为负，这些结果都表明投资者可能通过多样化获得更高的收益和更低的风险。

表4 各省股票收益相关系数

?

本研究的目的还包括对投资者进行多省分散化投资的优势进行实证检验。首先，必须计算出一系列股票的有效组合，有效组合被定义为在多支股票构成的全部投资组合中，给定收益率时标准差最小化的股票组合，或是给定标准差时收益率最大化的股票组合。满足上述条件的所有投资组合在坐标图上构成了有效边界，有效边界上的每一点代表着一种(或以上)不同投资比例的股票组合。

表5 多省分散化方差最小组合与最优组合的各省股票构成比例

在本部分，本文比较了13 个省份的投资组合，以及随机选出30 支股票构成的多省分散化投资组合的超额回报率和标准差。随机选出的30支股票来自15 个不同省份，每个省的股票有两支。如果随机产生的分散化投资组合能够产生更高的投资收益，或是更低的标准差，或者能构建出优于单个省份股票组合的有效边界，就可以支持分散化组合能给投资者带来更大价值的观点。从表5 可以看出，构建最小化标准差的多省分散化组合与最大化Sharpe 比率的多省分散化组合在各省股票的投资比重上相差较远。当投资者尝试构建风险最低的投资组合时，需要配置较高比例的浙江(14.32%)、河北(14.90%)、广东(14.39%)和山西(13.75%)的股票，其他省份股票比例则低于10%；而在最优资产组合中，江苏股票比例最高，占21.68%，其次则是福建股票的13.70%，和安徽股票的11.37%，其余省份的股票比例则低于10%。有趣的是，实证结果表明最小方差组合和最大Sharpe 比例组合的股票构成存在明显差异，在最小方差组合中占较大比例的股票并未在最优股票组合中作为主要部分。

图3 描绘了样本中单个省份股票的投资组合以及以多省份股票构成的投资组合，来自每个省的股票组合以及多省化投资组合的有效边界均由三种方式组合，分别是最小标准差组合、Sharpe 比率最大组合以及收益率最高组合(即100% 由收益率最高的一支股票构成)。由于Sharpe 比率最高的组合可以被视为各省股票组合中的最优组合，投资者在持有Sharpe 比率最高组合时能获得最大的收益风险比，因此各省通过比较分散化投资组合和单个省份的投资组合，本研究发现多省股票的组合在绝大多数情况下表现均优于单个省份股票构成的组合，可显著获得更高的平均收益以及更低的标准差，仅是在风险水平较低时表现不如浙江省股票组合。有趣的是，就单个省的股票组合而言，浙江省投资组合的有效边界显著优于其他省份的有效边界。

图3 各省股票组合及多省分散化股票组合的有效边界

总体而言，在对地区分散化投资的检验中，本研究发现运用Markowitz 模型在中国市场构建地区分散化的股票组合，能够获得比单一省份公司的股票组合更好的表现。了解资产组合理论的股票投资者可以通过股票交易数据构建地区分散化的最优投资组合，即Sharpe 比率最高组合。这与投资者要求的回报率或是风险无关，多省分散化组合与单一省份股票组合相比，更可能产生高收益和低风险的表现。

五、结论与讨论

本文以Markowitz 的投资理论框对地域分散化在资产配置中的优势进行了阐述。本文对比了多省分散化股票投资组合和单一省份股票投资组合，发现多省分散化组合能够得到比单一省份股票组合更优的有效边界，也就是说，通过地域分散化可以达到提高收益和降低风险的投资目标。

对投资者来说，进行资产配置时除了考虑进行上市公司的行业因素外，还需要分析地域因素对投资组合的影响。投资者如果过度集中投资于同一区域的股票，会由于相同地区资产的相关性较高而增大投资风险。尤其是当该地区受到不利消息影响时，这种风险有可能由于投资者的羊群效应而被放大。投资者构建一个公司多元、地域分散的资产组合，可以更好地控制风险。

证券公司及管理部门需要加强对投资者的教育，尤其是对个人投资者的教育。中国股票市场机构投资者表现出一定程度的地域偏好(赵静梅、吴风云、罗梅,2012[14])，而个人投资者的不理性程度更甚。投资者存在着熟悉效应、羊群效应等非理性行为，这些非理性行为使投资者更可能产生集中投资的倾向，需要证券公司和管理部门引导投资者理性投资，注重投资的长期收益性，增强投资者的整体理性度，减少投资者盲目跟风的倾向。