长期恒荷载作用下混凝土时变断裂试验研究

韩小燕，高洪波，吴智敏，马 鹏

（1.海南大学，海南 海口 570228；2.大连理工大学，辽宁 大连 116024）

1 研究背景

混凝土断裂力学作为研究混凝土裂缝发展机理及其定量描述的有效工具，自1961年Kaplan首次将断裂力学理论应用于混凝土材料以来，国内外学者主要是在不考虑时间相关性的单调加载静态断裂范围开展了大量的研究，在其裂缝扩展过程及断裂过程区、软化本构关系、断裂参数和破坏准则等多个方面取得了一系列较为成熟的研究成果，发展出了多个混凝土类准脆性材料的断裂模型，制定了多个推荐性试验方法。

服役中的大体积混凝土结构（混凝土大坝、核燃料储存体、隧道衬砌、桥梁桥肩等）处在长期荷载作用下，裂缝随服役时间推移而出现的时变断裂问题关系到结构的安全。在长期荷载作用下，考虑时间相关性的混凝土时变断裂与不考虑时间相关性的单调加载静态断裂有较大差异，而目前对于混凝土时变断裂问题的裂缝扩展、软化本构关系等研究还不够成熟。为了能够正确评价处于服役状态的混凝土结构中已有裂缝的稳定性和危害性，有必要开展在长期荷载作用下混凝土结构裂缝的形成与发展机理的相关研究。

在过去几十年里，国内外学者对时间相关性的时变断裂研究主要关注于加载速率对断裂行为的影响［1-5］。长期荷载作用下，加载速率较小甚至恒定而主要考虑断裂行为时间相关性的时变断裂试验周期长，公开发表的文献较少［6-11］。Bazant等［6］采用双边切口试件，分别在50%、70%和90%峰值荷载的恒荷载作用下偏心受压加载约1个月，记录了裂缝口张开位移CMOD（t）等相关试验数据，利用先前提出的时变断裂R阻力模型［7］分析了混凝土时变断裂裂缝扩展，试验结果表明混凝土的寿命主要由时变断裂引起的裂缝扩展所控制而非徐变。Bazant等［7］还提出时变断裂过程区的机理只是与裂缝张开率特征量有关，且裂缝张开率决定了裂缝扩展速度，尤其是在裂缝断裂过程的最后阶段。Zhou［8］通过荷载比为0.92、0.85、0.80、0.76；跨高比为8 的非标准三点弯曲梁试件及荷载比为0.9、0.8 的紧凑拉伸试件开展了长期荷载作用下的混凝土时变断裂研究，得出了不同长期恒荷载水平作用下的CMOD（t）-t曲线，并通过数值模拟验证了试验结果，结果表明在长期恒荷载作用下，紧凑拉伸试件寿命比三点弯曲梁长，且时变断裂CMOD（t）-t曲线分为3个阶段，其中第二阶段主导整个断裂过程。Carpinteri等［9］对已加载至下降阶段有局部损伤的试件进行了拉伸和弯曲徐变断裂试验，试验加载制度为，先按照单调加载静态断裂试验将试件加载至下降阶段不同预定卸载点后卸载，再加载至卸载点荷载的70%、75%、80%、85%、90%、95%，之后一直持载直至试件破坏。试验分析了P-CMOD，徐变阶段CMOD-t及荷载比P/Pmax-CMOD等关系，结果表明三个阶段特征同文献［8］结论相同，对于相同的徐变荷载水平，试件在下降段较小荷载点卸载时失效断裂寿命更短，表明高损伤引起的承载能力下降会导致混凝土断裂寿命缩短；混凝土单调加载静态断裂试验荷载-位移曲线的下降段可以作为徐变断裂的包络准则。Sarkhosh等［10］进行了荷载比为71%、75%和83%的三点弯曲梁时变断裂试验，并提出了基于虚拟裂缝模型的有限元方法以模拟时变断裂过程。文献［11］对三点弯曲梁试件分别进行了荷载水平为30%峰值荷载和起裂荷载的徐变试验，为期115 d，然后再对徐变后的试件进行单调加载静态断裂试验直至其破坏，根据试验结果计算了临界裂缝扩展长度，峰值荷载，断裂能和失稳韧度，并与未经徐变直接进行单调加载静态断裂试验的三点弯曲梁试件进行了对比。试验结果表明：低水平恒荷载对混凝土的断裂性能参数没有影响，而高水平恒荷载作用下，混凝土临界裂缝扩展长度和失稳韧度增大但断裂能及峰值荷载几乎不变。以上试验加载制度和试件型式各异，也未与单调加载静态断裂试验结果进行对比分析。因此有必要开展标准试件的长期恒荷载断裂试验，以便进行研究结果的相互比较验证，且长期恒荷载作用下的断裂试验周期长，有必要分析其与单调加载静态断裂试验结果的差异性规律。

本文采用标准三点弯曲梁试件，分别施加5个不同水平的恒定荷载，实时采集其裂缝口张开位移随恒载持续时间的变化直至试件发生断裂，分析时变断裂裂缝口张开位移CMOD（t）及裂缝口张开速率CMOR（t）随恒载时间的变化规律，时变断裂临界裂缝口张开位移CMOD（tc）及混凝土试件时变断裂寿命tcr与荷载比之间的关系，以期为后期研究时变断裂裂缝扩展和时变断裂能，揭示时变断裂机理提供基础试验数据。

2 试验概况

2.1 试件制备试验采用标准三点弯曲梁试件，其尺寸为L×B×D=515 mm×100 mm×100 mm，初始缝高比a0/D=0.4，跨高比S/D=4。混凝土试件配合比为水泥∶砂子∶石子∶水=1∶2.14∶3.34∶0.60。试验材料为海南天涯牌P·O 42.5级普通硅酸盐水泥，河砂，海口本地火山岩碎石，最大公称粒径为20 mm。

试件采用定制铸铁模板，待养护28 d后，用切片厚度为3 mm的云石切割机对试件进行切缝。其28 d强度为40.4 MPa。

2.2 试验方法在进行混凝土时变断裂试验之前，需用3个试件进行单调加载静态断裂试验，以此得出试件断裂所需最大荷载Pmax，其结果如表1所示。

表1 混凝土试件最大荷载Pmax （单位：kN）

对于时变断裂试验，现有的设备都很难满足所需要的长期恒定荷载，因此作者根据试验需求，自制了反力架加载装置（如图1所示），其可通过改变试件位置，利用杠杆原理可以施加所需荷载。如果所需恒荷载较大，除了依靠钢梁自重以外，还可以在端部放置重物。前期加载至恒定荷载所需时间控制在约5 min左右。加载过程中注意用千斤顶缓慢且较为匀速地放置钢梁杆杠，以防产生冲击荷载破坏试件。试验全程均在自然环境下进行，温度约为21～33℃，湿度约为70%RH～90%RH。表2为时变断裂试验所施加的各级恒荷载水平的数值大小。同时试验中所需监测的裂缝口张开位移CMOD（t）通过东华测试DH3816N静态应变仪实时采集夹式引伸计的读数来确定。

图1 长期恒荷载试验加载装置

表2 混凝土时变断裂的各级恒荷载P

3 试验结果与分析

3.1 时变断裂曲线CMOD（t）-t根据DH3816N采集到的夹式引伸计的一系列读数，用origin拟合出不同恒荷载水平作用下的CMOD（t）-t曲线，如图2—图7所示。其中，图2—图6中试验数据CMOD（t）起始值是准静态加载结束时刻测定的CMOD值。0.95Pmax荷载水平下CMOD（t）起始值为0.0329 mm；0.85Pmax荷载水平下CMOD（t）起始值为0.0314 mm；0.80Pmax荷 载 水平下CMOD（t）起始值为0.0264 mm；0.75Pmax荷载水平下CMOD（t）起始值为0.0247 mm；0.70Pmax荷载水平下CMOD（t）起始值为0.03 mm。

图2 0.95Pmax混凝土时变断裂CMOD（t）-t曲线

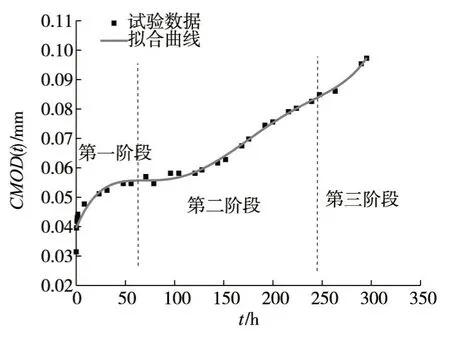
图3 0.85Pmax混凝土时变断裂CMOD（t）-t曲线

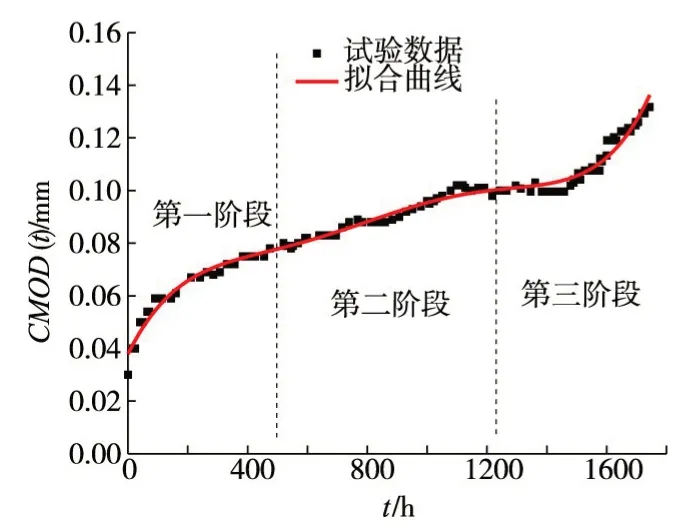
图6 0.70Pmax混凝土时变断裂CMOD（t）-t曲线

图7 不同荷载水平作用下混凝土时变断裂CMOD（t）-t曲线

由图可知：CMOD（t）在持载阶段不断增大，且CMOD（t）-t曲线呈现出3个阶段的特征：第一阶段，CMOD（t）快速增大；第二阶段，CMOD（t）平稳增长；第三阶段，CMOD（t）迅速增大直至试件断裂破坏。文献［6］认为，CMOD（t）三阶段增长的机理为：第一阶段主要是由块体中水泥浆材料的黏弹性行为引起的；第二阶段由块体中水泥浆材料的黏弹性行为和裂缝扩展共同作用；第三阶段主要是由裂缝扩展决定的。作者认为引起CMOD（t）3阶段增长的因素由两部分组成：断裂过程区外块体材料的徐变和断裂过程区虚拟裂缝的时变软化行为及其发展。第一阶段主要是断裂过程区外块体材料的徐变引起的；第二阶段由断裂过程区虚拟裂缝的时变软化行为及其发展和断裂过程区外块体材料的徐变共同作用；第三阶段主要是由断裂过程区虚拟裂缝的时变软化行为及其发展决定的。

由图可知，3阶段所占比例近似为30%、50%、20%，且荷载越大，第一阶段越不明显。其中第二阶段的长度决定了混凝土时变断裂的持续时间。CMOD（t）-t曲线的第二阶段斜率变化不大，曲线的斜率，即混凝土时变裂缝口张开速率CMOR（t）可用来预测混凝土时变断裂的寿命。部分曲线有跳跃现象，对此Bazant等［6］的解释为：在强度相对比较高的混凝土中，裂缝扩展倾向于穿过骨料而不是绕过。

3.2 时变裂缝口张开速率CMOR（t）CMOR（t）反映了混凝土时变断裂过程中不同时刻裂缝口张开位移CMOD（t）的增长速率。其计算方法是：对试验数据拟合出来的CMOD（t）-t曲线求一阶导数。各级恒荷载水平下的CMOD（t）-t曲线如图8—图12所示。

CMOR（t）-t曲线代表着CMOD（t）-t曲线的斜率，因此也呈现出与CMOD（t）-t曲线类似的三个阶段特征：第一阶段，裂缝口张开速率CMOR（t）逐渐减小；第二阶段，裂缝开始平稳发展，其裂缝口张开速率CMOR（t）几乎不变；第三阶段，试件进入失稳阶段，裂缝口张开速率CMOR（t）快速增大，直至其断裂破坏。

3.3 临界裂缝口张开口位移CMOD（tc）在单调加载静态断裂试验中，CMODc为最大荷载Pmax所对应的裂缝口张开位移，在试验过程中可通过静态应变仪读数确定，其结果如表3所示。

对于时变断裂试验，CMOD（t）-t曲线第二阶段是混凝土断裂过程中最重要的一阶段，其中第二阶段与第三阶段的交点纵坐标即可作为混凝土时变断裂失稳破坏控制参数。由于从CMOD（t）-t曲线中很难直观地看出第二阶段和第三阶段的分界点，本文通过CMOR(t)的一阶导数CMOR′(t)确定CMOD（tc）的具体数值。各级恒荷载水平下混凝土试件的CMOR′(t)-t曲线如图13—图17所示。

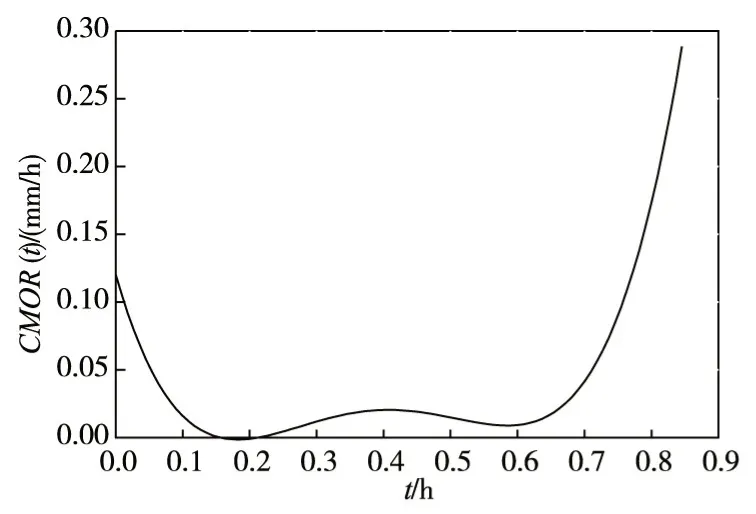
图8 0.95Pmax时变断裂CMOR（t）-t曲线

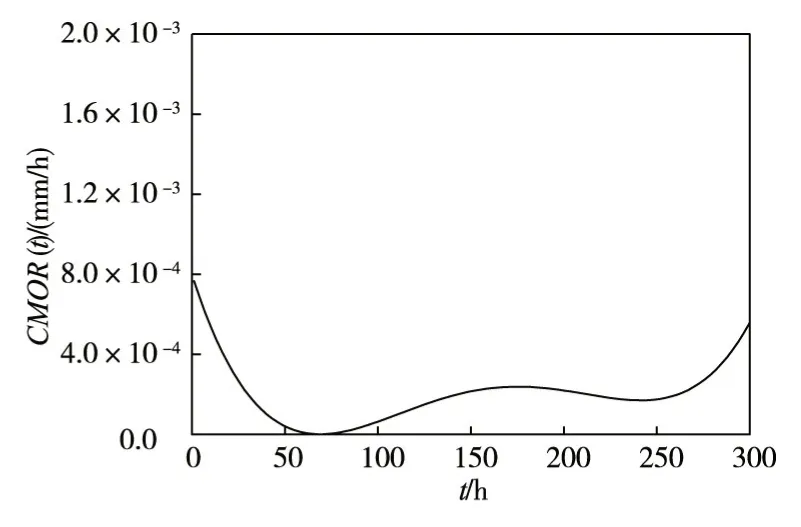
图9 0.85Pmax时变断裂CMOR（t）-t曲线

图10 0.80Pmax时变断裂CMOR（t）-t曲线

图11 0.75Pmax时变断裂CMOR（t）-t曲线

图12 0.70Pmax时变断裂CMOR（t）-t曲线

表3 单调加载静态断裂试验CMODc值 （单位：mm）

以0.95Pmax为例，图13为CMOR′(t)-t曲线，该图中间段纵坐标值接近于0，说明CMOD（t）-t曲线在该阶段近似以恒定的速率增长，即曲线的第二阶段；而最后阶段纵坐标为正值且呈现出明显的单调递增趋势，即为CMOD（t）-t曲线的第三阶段。则CMOR′(t)-t曲线与横坐标交点的最大值tc=0.55 h可近似认为是CMOD（t）-t曲线第二阶段与第三阶段的交点横坐标，即临界时刻，其对应的裂缝口张开位移即为本文所求的临界裂缝口张开位移CMOD(tc)。以此类推得到各级恒荷载水平下的时变断裂临界裂缝口张开位移CMOD(tc)如表4和图18所示。

由表4及图18可以看出，与不考虑时间相关性的单调加载静态断裂试验相比，时变断裂试验的临界裂缝口张开位移CMOD(tc)偏大；随着恒荷载水平的增大，时变断裂临界裂缝口张开位移CMOD(tc)减小且接近单调加载静态断裂的临界裂缝口张开位移CMODc。

图13 0.95Pmax恒载CMOR′（t）-t曲线

图14 0.85Pmax恒载CMOR′（t）-t曲线

图15 0.80Pmax恒载CMOR′（t）-t曲线

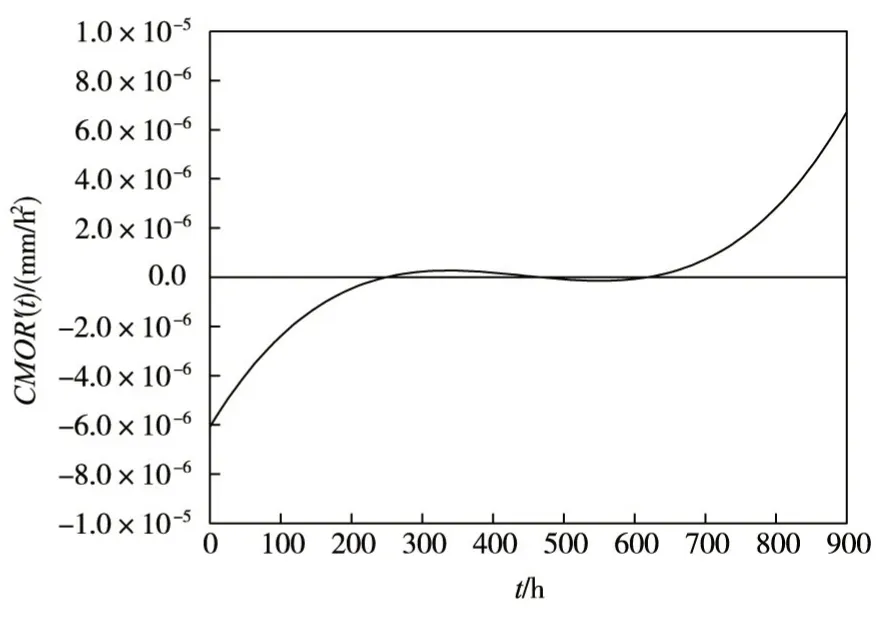
图16 0.75Pmax恒载CMOR′（t）-t曲线

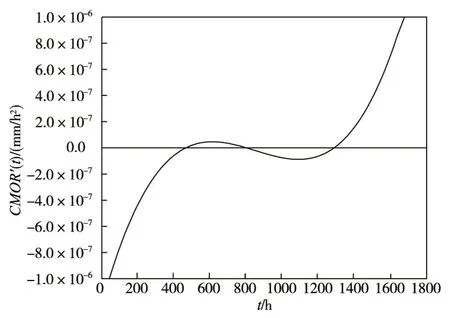
图17 0.70Pmax恒载CMOR′（t）-t曲线

表4 各级荷载水平下临界裂缝口张开位移

Zhou［8］对三点弯曲梁试件分别进行了应力比为0.92、0.85、0.80、0.76 的时变断裂试验研究。其中，试件尺寸为L×D×B=840 mm×100 mm×100 mm，S=800mm，a0=50mm。该试验结果的临界裂缝口张开位移如表5 和图19所示。由表中数据可得出与本文试验一致的结论，在时变断裂试验中，临界裂缝口张开位移CMOD(tc)会随着恒荷载水平的增大而减小。

表5 文献［8］中各级荷载水平下临界裂缝口张开位移

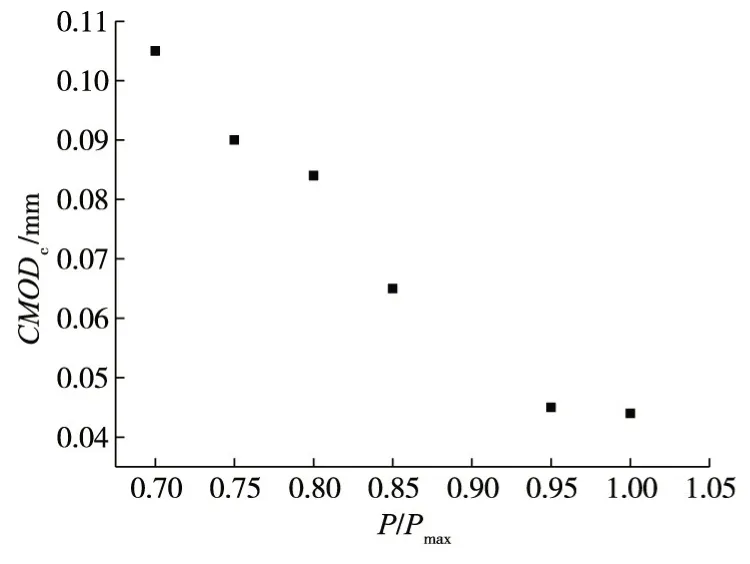
图18 各级荷载水平下混凝土临界裂缝口张开位移CMODc

图19 文献［8］中各级荷载水平下混凝土临界裂缝口张开位移CMODc

3.4 时变断裂寿命tcr在CMOD(t)-t曲线第三阶段中，当CMOD(t)-t曲线斜率接近于无穷大时，就意味着混凝土试件断裂，寿命终结，混凝土从开始加载到最终断裂的时间即为混凝土断裂寿命tcr。各级荷载水平下的试件tcr结果如表6所示。

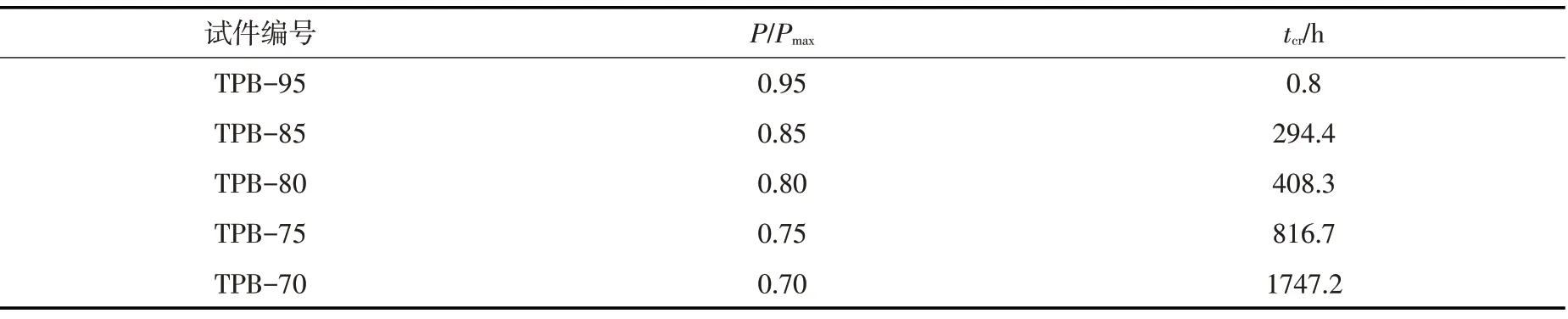
表6 各级荷载水平下混凝土时变断裂寿命tcr

由表6 可知，对于不同恒荷载水平的试件，其寿命tcr随着长期恒荷载水平的增大而减小。0.70Pmax荷载下的试件，试验周期接近72 d。根据本试验的试验数据用origin拟合出混凝土试件时变断裂寿命tcr与荷载比P/Pmax曲线，如图20所示。其拟合曲线表达式为：

图20 试件寿命tcr与荷载比P/Pmax曲线

Bazant等［6］用双边切口的试件进行了偏心率为e=D/8的偏心受压加载，并通过试验数据及R阻力模型计算的理论寿命得出结论：对于一系列几何相似但尺寸变化的试件而 言，预测寿命似乎随着试件尺寸的增大呈现轻微地减小趋势。但由于试验数据具有离散性，上述尺寸效应几乎可以忽略不计，恒荷载水平是决定寿命的主要因素。Zhou［8］也指出：混凝土时变断裂寿命与恒荷载比成指数关系。本文试验结果与两篇文献的结论类似，得到荷载比是混凝土试件时变断裂寿命tcr的主要影响因素，如公式（1）所示的指数关系。

4 讨论

混凝土徐变是结构或材料承受的应力不变，应变随时间增长的现象。混凝土徐变是连续介质力学范畴内，从整体荷载和变形角度出发的概念。早期文献中，研究者把考虑混凝土徐变对断裂行为影响的断裂问题称为徐变断裂。而从混凝土断裂力学角度，随着裂缝的扩展，断裂过程区的黏聚力分布是不断发展变化的。因此，严格来说，混凝土断裂破坏过程中无法满足应力持续不变的条件。混凝土徐变断裂用于考虑时间相关性的混凝土断裂问题不够准确。

另外，随着研究的深入，国内外研究者认识到，考虑时间相关性的断裂行为不仅与断裂韧带外实体部分材料的徐变有关，还与断裂过程区的黏聚裂缝张开速率有关［6］。近年来国外文献［4-6，8-10］逐渐把考虑断裂行为时间相关性的断裂表述为time-dependent fracture，以区别于单调加载静态断裂。作者在本文研究中认识到，考虑时间相关性的断裂行为不仅与断裂过程区外块体材料的徐变有关，而且更重要的是由断裂过程区虚拟裂缝的时变软化行为及其发展所决定的，因为裂缝的扩展及裂缝张开速率本质上取决于断裂过程区混凝土的时变软化行为。因此，作者认为把此类需要考虑断裂过程区外材料的徐变和断裂过程区虚拟裂缝时变软化行为的时间相关性断裂问题，中文称谓“时变断裂”较为恰当。

5 结论

本文采用标准三点弯曲梁试件分别进行了荷载水平0.7Pmax、0.75Pmax、0.8Pmax、0.85Pmax和0.95Pmax的时变断裂试验，监测了试件持载过程中的裂缝口张开位移CMOD（t）数据；分析了CMOD（t）及裂缝口张开速率CMOR（t）与时间t的关系曲线，计算了时变断裂临界裂缝口张开位移CMOD（tc），并与不考虑时间相关性的单调加载静态断裂试验CMODc进行了对比，考虑了混凝土试件时变断裂寿命tcr与荷载比之间的关系。基于试验及数据分析结果可以得出以下结论：（1）标准三点弯曲梁试件和其他试件型式的混凝土时变断裂CMOD（t）-t曲线类似，CMOD（t）在持载阶段不断增大，呈现出三阶段特征：第一阶段，CMOD（t）快速增大；第二阶段，CMOD（t）平稳增长；第三阶段，CMOD（t）迅速增大直至试件断裂破坏。（2）混凝土时变裂缝口张开速率CMOR（t）参数，能够直观描述混凝土时变断裂裂缝口张开位移CMOD（t）的变化规律。CMOR（t）-t曲线也呈现出三阶段特征：第一阶段CMOR（t）逐渐减小，反映了CMOD（t）增长变缓；第二阶段CMOR（t）-t几乎不变，反映了CMOD（t）平稳增长；第三阶段CMOR（t）快速增大直至断裂破坏，反映了CMOD（t）在此阶段迅速增大，失稳破坏。（3）长期恒荷载作用下的混凝土时变断裂，第二阶段裂缝稳定扩展，第三阶段裂缝失稳扩展，两个阶段的交点即为混凝土时变断裂失稳破坏临界时刻，其对应的临界裂缝口张开位移CMOD（tc）可作为时变断裂失稳破坏控制参数。失稳破坏临界时刻tc可通过本文提出的方法即CMOR(t)的一阶导数CMOR′(t)确定。（4）与不考虑时间相关性的单调加载静态断裂试验相比，时变断裂试验的临界裂缝口张开位移CMOD（tc）偏大；随着恒荷载水平的增大，时变断裂临界裂缝口张开位移CMOD（tc）减小且接近单调加载静态断裂的临界裂缝口张开位移。（5）混凝土试件从开始加载到最终断裂所需要的时间定义为其时变断裂寿命tcr。在时变断裂中，CMOD（t）的斜率CMOR（t）接近无穷大时就意味着试件寿命终结。对于不同恒荷载水平的试件，其时变断裂寿命tcr随着长期恒荷载水平的增大而减小，且荷载比是混凝土试件时变断裂寿命tcr的主要影响因素，混凝土试件时变断裂寿命与荷载比P/Pmax成指数关系。