剪缩型土的剪胀性大数据特征与计算模型

杨骏堂，刘元雪，何少其

（陆军勤务学院 岩土力学与地质环境保护重庆市重点实验室，重庆 401311）

1 研究背景

土作为多孔多相材料，其体积会随着剪切作用，发生体胀或体缩，前者称为“剪胀”，后者常被称为“剪缩”，这种性质被广义地称作剪胀性［1］，它是土区别于其他材料的重要特性［2］，也是建立本构模型［3］的基础。因此，对土的剪胀性研究一直是岩土工程领域的热点问题。国外学者针对土的剪胀性开展了大量研究。Reynolds［4］揭示了砂土体积变化是因为粒子之间存在跨越现象而产生的。Rowe［5］将应力与体积变化联系起来，提出了应力剪胀理论，并认为土的剪胀性是由内部几何约束引起的。Been和Jefferies［6］提出了描述粗粒土剪胀变形的状态参数ψ。Cubrinovski和Ishihara［7］通过实验发现剪胀率与塑性剪应变有关。Li 和Dafalias［8］将剪胀性与材料的当前状态紧密联系起来。Yang等［9］通过引入修正剪胀系数，建立了一种考虑剪胀效应的剪胀模型。Li等［10］在对粉质黏土的三轴实验中，发现了剪胀率与塑性剪应变之间存在明显的非线性关系。

近十几年来，国内学者也取得了丰富的研究成果。李广信等［11］认为，土的剪胀变化来源于土颗粒从低能状态向高能状态的变化，其大部分剪胀会随着卸荷而恢复。张建民［12］认为砂土存在可逆性剪胀是相对滑移机制和平均定向率的可逆变化共同作用的结果。刘元雪等［13］提出土体的可恢复性剪胀可部分归因于土的各向异性引起的弹性剪胀。黄茂松等［14］基于特征状态应力比和初始围压对修正剑桥模型中的剪胀方程进行了改进。栾茂田等［15］利用含有主应力方向的砂土状态参数建立了剪胀方程。迟明杰等［16］基于细观力学的思想，对砂土剪胀机理开展了探索，并得到了新的剪胀模型。熊焕等［17］提出了一种非共轴因子，并应用于剪胀模型。孙逸飞等［18］基于分数阶梯度律，从理论层面提出了一种分数阶状态依赖的剪胀方程。刘嘉英等［19］基于状态相关理论，采用应力洛德角作为模型参数，提出了一个三维剪胀模型。朱晟等［20］分析了粗粒土的级配与剪胀性的关系，并建立了相应的剪胀模型。

学者们从能量、状态参数和微观组构等角度来解释剪胀机理，并建立了大量模型，但这些模型的通用性却不尽人意。由于土体剪胀模型的研究是一个较为复杂的问题，它与土体类别和内外影响因素均有关系，仅考虑单一因素对剪胀性的影响不够合理，因此笔者认为可以在考虑剪胀性影响因素的综合作用基础之上，开展土体剪胀性共同规律的研究。通过对不同土类的应力应变关系进行研究和统计分析，根据体应变在剪应力作用下的变化特征可将土分为两类：一类是剪缩型土，即在剪应力作用下，只发生体积压缩，包含正常固结土、松砂等；另一类是剪胀型土，即在剪应力作用下，初期发生体积压缩，随着土体密实度的增大，再发生体积膨胀，包含超固结土、密砂等。从两类土的变化特征看，剪胀型土的变化过程显然更为复杂，同时剪缩阶段可视为其剪胀性变化的前序阶段，所以当研究剪胀型土的时候，不仅需要研究剪胀阶段，更需要结合剪缩阶段的变化特性进行分析。综上，剪缩型土的研究会对剪胀型土的分析奠定一定的研究基础，同时对剪胀型土的研究，以及对研究剪缩型土和剪胀型土的统一问题具有积极的现实意义。

近年来，大数据深度挖掘技术在岩土本构关系领域的应用［21-23］上表现了突出的能力。说明了大数据技术在剪缩型土的剪胀性研究上也是可行的。本文首先基于MapReduce的并行化计算框架，提出一种并行化的LM优化算法。然后对大量的剪胀性实验数据进行特征挖掘，分别建立剪胀率与其影响因素之间的相关性函数。在此基础上，考虑剪胀率各影响因素的综合作用，建立新的剪胀模型。

2 一种并行化的LM优化回归算法

在本文研究中，需要在剪缩型土试验大数据的基础上，建立关于剪胀率d与其各影响因素之间的相关性函数。对于传统回归算法，一方面收敛性较慢，计算不稳定；另一方面在处理大规模数据时效率低下。为了解决以上问题，本文提出了一种基于MapReduce计算框架的并行化LM优化回归算法。

2.1 Levenberg Marquardt（LM）算法在进行回归分析时，Gradient Descent（GD）法、Newton 法、Gauss-Newton（GN）法以及Levenberg-Marquardt（LM）法被广泛使用。GD法可表示为［24］：

式中：α为迭代步长；g为负梯度方向，也就是梯度下降方向。Newton法可表示为［25］：

式中：H-1为迭代步长，H为Hessian矩阵。

GN法是Newton法的改进方法，它利用雅可比矩阵J替代H矩阵，可表示为［24］：

式中，J T为雅可比矩阵的转置矩阵。在Newton法中，需要求解H，运算量大，不利于实现，所以通常在Newton法的基础上利用JTJ近似H，省略了H的复杂计算，也就是GN法，从而一定程度上保证了计算效率，但由于迭代步长需要保证H是正定的，但是在实际计算中，H很有可能是半正定或者其他情况，因此在使用GN法时，稳定性差，还可能存在不收敛的情况。正是考虑到H的正定性问题，基于信赖区域理论，引入了一个约束，从而保证算法更具普适性。LM算法中的迭代公式可表示为［26］：

从式（4）可知，H≈JTJ+λI，I表示单位矩阵，λ为学习参数。当λ＞0时，恒为正值，这也就确保了迭代步长是正定的。当λ=0时，式（4）可转化GN法；当λ=∞时，式（4）可转化GD法。LM算法的好处在于，当梯度下降的太快，可使用较小的λ；当梯度下降的太慢，又可使用较大的λ。使用LM算法解决了收敛性慢等问题，所以能表现出良好的性能。本文在Kaggle数据库的回归型数据子库中选择了500条数据，作为比较不同算法效果的实验数据。在进行实验之前，从500条实验数据中随机抽取200条数据构成一组训练数据，以此方法，得到10组训练数据，再分别利用GD法、GN法和LM算法进行回归训练，比较结果如表1所示。

表1 不同回归算法的比较

从表1可以看出，LM算法相比于传统的回归算法，收敛速度更快，鲁棒性更好。

2.2 MapReduce并行化计算框架首先将大量待处理数据划分为若干块，然后交由并行化框架中的Map 作业节点分别计算，运算结束后，再通过Reduce 阶段组合［27］。根据运行顺序，可把MapReduce框架分成如图1所示的4个阶段。

图1 MapReduce并行化框架的流程图

（1）Split阶段。在Map阶段之前，系统会根据输入文件计算Split个数，每个Split文件会对应一个Map任务，此时Split文件中存储的不是待处理数据，而是一个Split文件的长度和一个记录数据所在存储位置的数组。

（2）Map阶段。可根据实际算法需要，自定义Map阶段的处理逻辑函数，然后各Map作业节点会读取对应的文件，并将文件解析成为键值对。一般地，键（Key）指一组数据的所在位置，值（Value）指该组数据的具体元素，因此可用一个键值对来表示一组数据。

（3）Combine阶段。这是一个可根据实际算法需要自定义的函数，主要对Map阶段所得到键值对进行相应处理，一般情况下是做一个合并重复键的操作。

（4）Reduce阶段。即执行Reduce函数，将所有结果进行全局汇总并存储到对应的文件中。

通过以上分析可知，在传统回归算法中，每次迭代都必须要遍历所有数据，所以计算效率低下。采用MapReduce 并行化计算框架可将负责的大任务分解成若干个小任务，让集群中的多个工作节点并行化地执行，从而大大提高运行效率和计算稳定性。

2.3 基于MapReduce的LM优化回归算法在2.1节和2.2节的研究基础上，提出了基于MapReduce框架的LM优化回归算法。需要注意的是，在Map阶段进行拆分的前提是子任务可以并行计算，即彼此之间没有依赖关系，相互独立。因此，研究LM算法中的可并行化过程，是提高算法运行效率的必要手段。在本文MapReduce并行化框架下的LM算法的具体迭代流程为：

①初始化参数。k=0；v=2；x=x0；Α=JTJ；g=JTf；

②根据如式（5）所示的迭代公式，求解hlm（hlm为迭代步长）；

④分别计算式（6）和式（7）；

⑤如果ρ＞0，则有式（8）和（9）；

如果g≤ε1，则结束循环，并且有式（10）；

⑥如果ρ≤0，则有式（11）；

⑦跳转到第②步。

通过对以上迭代过程的分析，可发现步骤②、④和⑤具有完全的可并行性，因此可将其完全应用于本文建立MapReduce 并行化计算框架。为了验证本文提出算法的优越性，在Kaggle 数据库的回归型数据子库中选择了20 000 条数据，然后从中随机选择10 000 条数据构成一组训练数据，以此方法，得到10 组训练数据作为比较不同算法效果的实验数据。分别利用GN 法、LM 算法和本文提出的基于MapReduce的LM优化回归算法在不同数据量下进行回归训练，比较结果如图2所示。

从图2 可知，本文提出的基于MapReduce 的LM优化回归算法在不同数据量下的训练时间明显少于传统训练算法，表明利用MapReduce 计算框架后算法的效率和稳定性都得到显著提升。

图2 不同数据量下训练效果比较

3 剪缩型土的剪胀计算模型

剪胀性数据收集的代表性和可靠性是保证本文研究的重要条件。因此本文在对数据进行收集时从数据的来源、提取和检验三个过程进行严格控制。

（1）数据来源的控制。本文数据主要取自表2所示的权威刊物中发表的论文资料，相比于其他数据来源，可以说从源头上确保了数据的代表性和可靠性。

（2）数据提取的控制。一方面由于应力路径对土的剪胀性影响比较复杂，考虑到常规三轴压缩试验在实际应用中较为普遍，数据丰富并且较易获取。因此在本文研究中要求试验数据必须来源于常规三轴压缩试验的土样本。另一方面选择的土样本需要根据剪缩型土的基本力学特性，如体应变、应力增量和剪胀率恒大于0等条件来去除不符合的试验数据，并且其体应变随轴向应变的变化趋势需要符合图3 中曲线所示。同时在提取试验数据点时，必须按照实际的试验点进行提取，并且要求提取的数据点不少于25个。因为如果数据点提取的过少，会影响到应力应变关系的真实表达。严格控制数据的提取过程进一步确保了数据的可靠性。

表2 文献主要来源表

（3）数据检验的控制。考虑到在第（1）和（2）过程中可能出现的人为因素影响，将课题组分为两个小组，严格按照上述过程进行交叉检验，最终得到了215个剪缩型土样本，并计算得到相应的剪胀性数据，其中部分土样本的数据如表3所示：d表示剪胀率，p表示平均球应力，q表示广义剪应力，dp、dq分别表示平均球应力和广义剪应力的增量，分别表示塑性体应变和塑性剪应变。

图3 剪缩型土中εv与ε1 的关系

表3 部分剪缩型土样本的实验数据

3.1 剪胀率的影响因素剪胀率d是衡量土体剪胀性的重要指标。因此对d的相关影响因素的研究显得尤为必要。在应力剪胀理论［5］中，认为d与应力比q p唯一相关。文献［7］指出d会受到塑性剪应变的影响。考虑到塑性体应变也是描述土体剪胀性的一个重要参数，所以表明d与也存在相关关系。岩土材料不同于其他材料，其变形过程不仅取决于当前应力的状态，还会受到应力增量状态dp和dq的影响。综上分析，本文利用215个剪缩型土样本的剪胀性数据，分别计算了d与的相关系数，结果如图4所示。

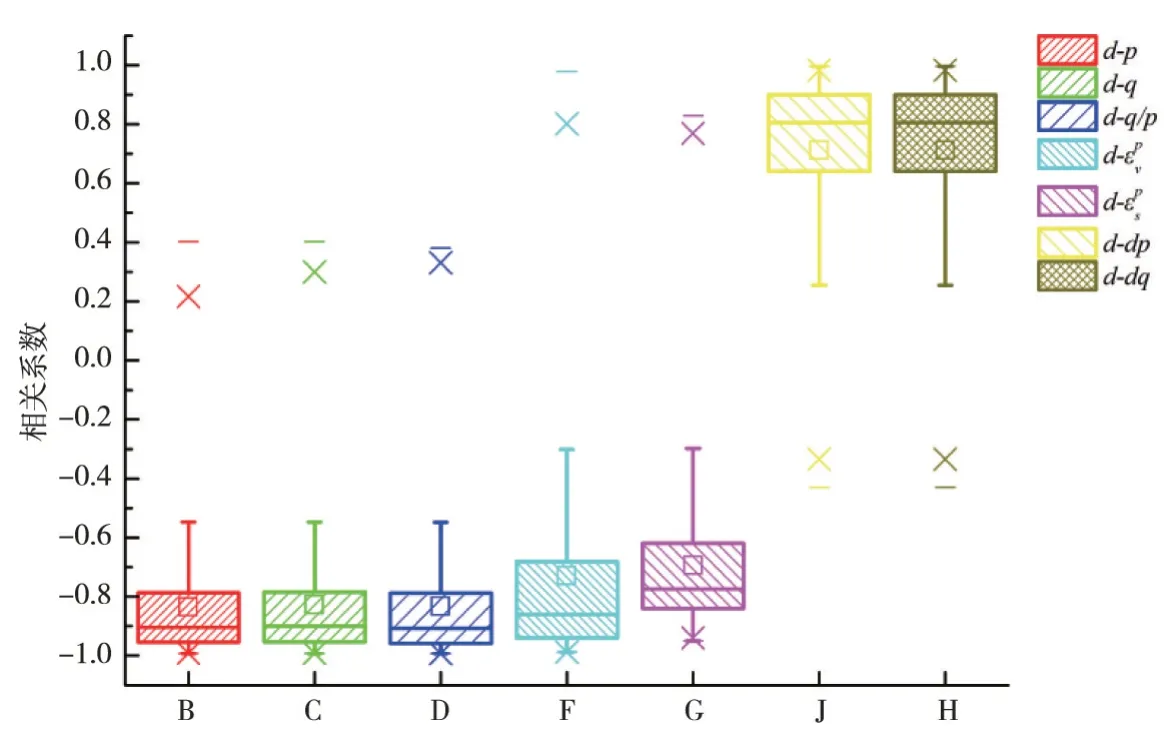
图4 剪胀率与不同因素之间的相关系数

从图4可知，剪胀率d与应力参数的相关系数均值达到-0.82，表明d与呈高度负相关；剪胀率d与应变参数的相关系数均值达到-0.69，表明d与呈显著负相关；剪胀率d与应力增量参数dp、dq的相关系数均值达到0.71，表明d与dp、dq呈显著正相关。考虑到一方面应力参数p、q处于同一量级，另一方面在以往的研究中多采用作为研究对象，并且d与的相关性更强，且远高于，所以在本文中选择作为d的主要影响因素，而将作为d的附加影响因素进行研究。

3.2 剪胀率与主要影响因素之间的相关性函数在本节中，基于剪缩型土的剪胀性大数据特征，再根据其基本力学特性和本文提出的并行化LM优化回归算法，建立了剪胀率与主要影响因素之间的相关性函数。

Cubrinovski等［7］提出，研究土的剪胀性的最佳方法是绘制d随应力比变化的曲线。d随（可记作η）的变化可分为以下三个阶段。①当η=0 时，d=∞，土体呈现等向压缩的变形特性；②当0＜η＜M（M为临界状态时的应力比），d＞0，土体处于剪缩变形阶段；③临界状态时，有η=M，d=0。考虑到剪缩型土样本中η范围差别较大，所以基于对进行归一化处理，如下式所示：

表示归一化后的η，根据如图5所示的d与的大数据特征，依据上述①—③的变形阶段，并参考修正剑桥模型和统一硬化理论［28］，可提出相关性函数，如下式所示：

式中：为所对应的临界状态应力比；dη为主要影响因素η所对应的剪胀率，通过本文提出的并行化LM 优化回归算法，即可得到如图5 中所示的拟合曲线。此时参数为：n1=3.862，n2=2.154，n3=1.027，拟合度为0.744。由此发现，仅利用主要影响因素η得到的剪胀模型，虽然可以大致地描述剪胀率的变化特性，但却不能与实际值良好吻合，因此本文考虑了剪胀率附加影响因素的作用，以期建立一个更为科学合理的剪胀模型。

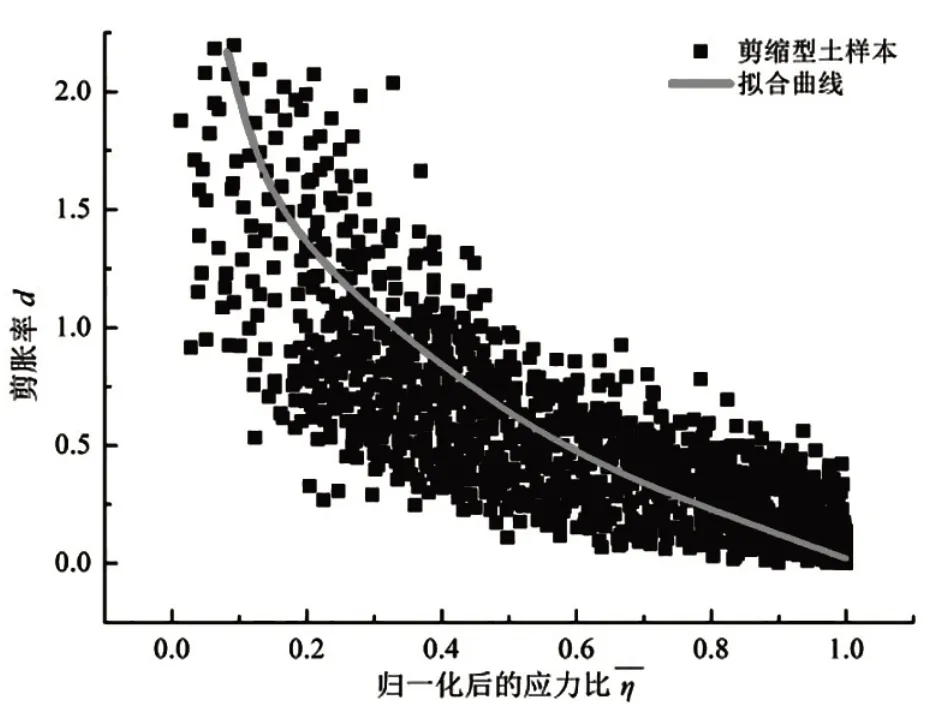
图5 d与η¯的大数据特征

3.3 剪胀率与附加影响因素之间的相关性函数在3.2节中，已研究了η对d的影响，并得到了dη与η的相关性函数。本节中利用式（14）即可得到附加因素对d的影响：

式中，da表示纯考虑应力比η的剪胀率误差，也是附加影响因素对剪胀率影响的比例。

本节主要研究da与附加影响因素之间的相关关系。

3.3.1da与的相关性函数 根据剪缩型土的基本力学特性可知，塑性体应变在剪切作用下逐渐增大。考虑到剪缩型土样本中范围差别较大，本文将归一化后再进行研究，归一化方法如下式所示：

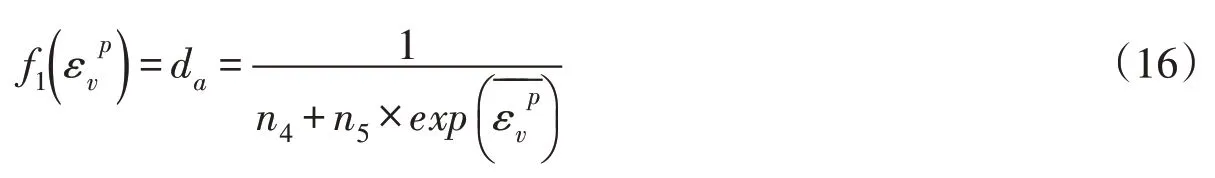
通过本文提出的并行化LM 优化回归算法，即可得到如图6 中所示的拟合曲线。此时参数为：n4=-7.912，n5=10.564，拟合度为0.704。

图6 da与的大数据特征

3.3.2da与的相关性函数 根据剪缩型土的基本力学特性可知，塑性剪应变在剪切作用下逐渐增大。考虑到在临界状态下仍然会继续增大，所以本文将初始临界状态（initial critical state）时的记作。又因为剪缩型土样本的范围差别较大，因此可基于对进行归一化处理，如下式所示：

da与的大数据特征关系如图7所示，da随着的增大而逐渐减小，当时，da趋近于0。因此可提出da与的相关性函数，如下式所示：

通过本文提出的并行化LM 优化回归算法，即可得到如图7 中所示的拟合曲线。此时参数为：n6=-17.359，n7=19.681，拟合度为0.685。

图7 da与的大数据特征

3.3.3da与dp、dq的相关性函数 考虑到剪缩型土样本中dp、dq范围差别较大，因此选择先期固结压力Pc分别对其进行归一化处理，如下式所示：

图8 da与应力增量的大数据特征

从图8可知，da分别随着的增加而逐渐变大，因此可提出da分别与dp、dq的相关性函数，如下式所示：

通过本文提出的并行化LM优化回归算法，即可得到如图8中所示的拟合曲线。此时式（21）中参数为：n8=0.009，n9=0.342，n10=1.091，拟合度为0.674。此时式（22）中参数为：n11=0.026，n12=1.026，n13=1.079，拟合度为0.673。

3.4 基于剪胀性大数据特征的计算模型从3.2与3.3节可知，基于大量剪缩型土样本实验数据建立的剪胀率与各影响因素之间的相关性函数拟合度均较低，这表明了剪胀率不能只考虑单一影响因素的作用，而是需要综合考虑主要因素和附加因素的影响。da与之间的相关性函数实际上包含了所有附加影响因素的作用，因此在总的剪胀模型中需要根据它们的相关性差异进行加权处理。本文计算了da与各附加影响因素之间的相关系数，结果如表4所示。

表4 da与各附加影响因素之间的相关系数

由此可计算出各附加因素对da影响的权重值，如下式所示：

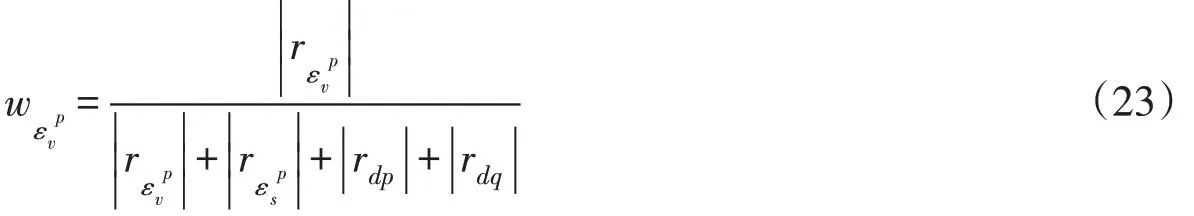
表5 剪胀模型的参数值

4 剪胀模型的检验

4.1 剪胀模型的比较剑桥模型和修正剑桥模型中的剪胀方程是经典的剪缩型土剪胀模型，在本文中分别记作模型1和模型2，如下式所示：

式中，M表示临界状态时所对应的应力比。

本文模型是在剪缩型土的大量实验数据特征挖掘基础上，再根据其基本力学特性和LM优化回归算法建立的，所以它不同于一般统计学意义上的计算模型，而是具有一定理论意义和应用背景的。为了验证本文模型的适用性和准确性，本文重新选择了一组独立的未参与之前模型建立的实验数据作为测试数据集。一般地，用于建立模型的训练数据和测试数据的数量之比为7∶3，所以测试数据集包含了92个剪缩型土样本。作为测试数据集的剪缩型土样本同样也取自于表2 中的文献实验数据，并且测试数据集的选择标准也与训练数据集相同。本文将测试数据集分别在剑桥模型和修正剑桥模型下的剪胀方程以及本文模型（见式（24）和表5）下进行比较，结果分别如图9—图11所示。

图9 模型1下剪胀率实验值与预测值比较

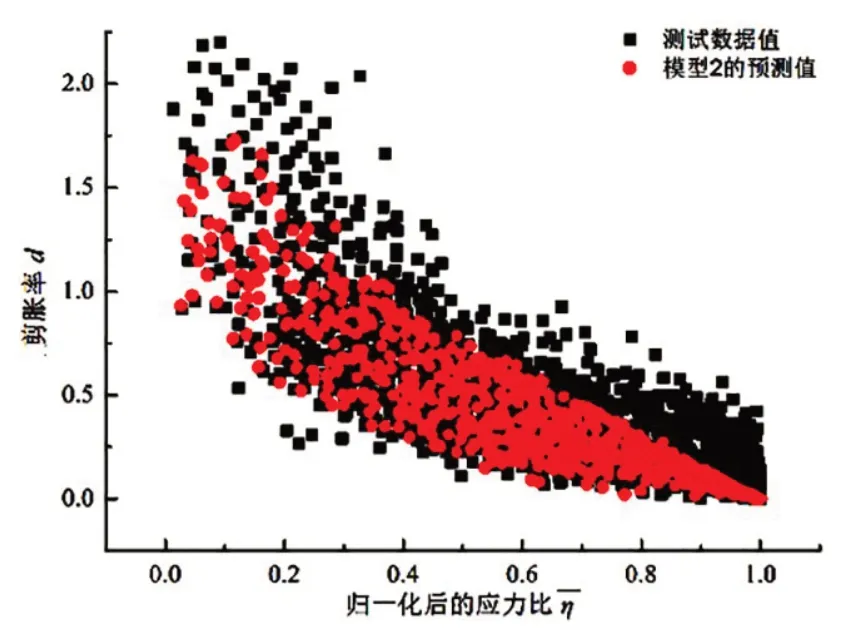
图10 模型2下剪胀率实验值与预测值比较

从图9可知，模型1与本文测试数据组的剪胀率拟合度为0.484，虽然能够大致描述其剪胀率的变化趋势，但不能与实验值良好吻合。特别是当剪胀率较大时，模型效果不理想。这是因为它只能反映d与η之间的线性关系，而从剪缩型土的d与η的大数据特征可知，二者呈明显的非线性关系。

从图10可知，模型2与本文测试数据组的剪胀率拟合度为0.646。相较于模型1，模型2效果有所提高，这是因为后者可描述d与η的非线性特征关系，但同时也存在着低估其剪缩性的问题，具体表现为在模拟较大的剪胀率时，模型效果仍然欠佳。

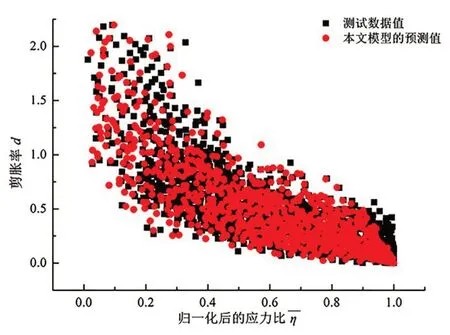
图11 本文模型下剪胀率实验值与预测值比较

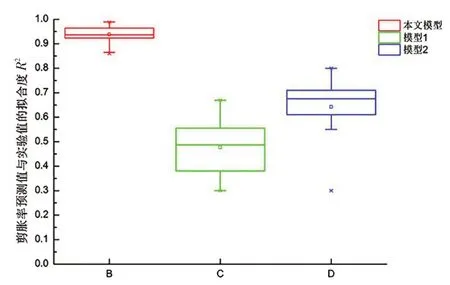
图12 不同剪胀模型下剪胀率拟合度的箱型图

在图11中，本文模型（见式（24）和表5）与测试数据组的剪胀率拟合度为0.938，相比于模型1和模型2，本文模型效果明显提高。一方面这是因为本文模型能够良好的描述d与η的非线性特征关系，另一方面则是因为考虑了剪胀率各影响因素的综合作用，从而解决了剪缩性在剪缩阶段被低估的问题。

图12为不同剪胀模型下的剪胀率预测值与实验值拟合度的箱型图，它可用于反映个体剪缩型土样本的拟合度预测结果的分布特征，还可以用于多组数据分布特征的比较。从图12可知，模型1和模型2的箱型图分布范围较宽，均值较小，表明各土样本的拟合度范围差别较大，并且拟合精度较低；本文模型的箱型图分布范围窄，均值大，表明各土样本的拟合度差别小，并且拟合精度高。综上分析，无论从总体统计还是个体样本来研究，本文模型的拟合精度结果相较于模型1和模型2都显著提高。

4.2 剪胀模型的验证为了进一步验证本文模型的适用性，选择未参与本文剪缩型土样本统计的文献［29］中Bothkennar 原状黏土在不同应力路径下的实验数据。Bothkennar 原状黏土试验的多种应力路径如图13所示。其中，路径4 表示在等q作用下，p逐渐减小的应力路径，此时土在剪切作用下体积膨胀。路径5 初始阶段为常规三轴压缩路径，到达p轴后，为常规三轴伸长路径。由于本文模型研究的是剪缩型土在常规三轴压缩实验条件下的剪胀变化特性，因此在对本文模型进行验证时，选择剪缩型路径1—3。不同应力路径下的剪胀模型预测值与实验值的比较情况如图14所示。为了量化不同应力路径下剪胀模型的拟合效果，剪胀率的实验值与三种剪胀模型下的预测值之间的欧式距离如表6所示。

从图14和表6可知，本文模型在三种不同应力路径下的欧式距离均值为0.156，基本保持在相对较小的范围内，表明剪胀率预测值与实验值能良好吻合；模型2在三种不同应力路径下的欧式距离均值为0.711，表明剪胀率预测值与实验值的变化趋势基本符合，但是在剪缩阶段却低估了其剪缩性，表现为预测值偏小；模型1在三种不同应力路径下的欧式距离均值为2.038，说明预测值与实验值误差相对较大，这是因为在该模型下剪胀率预测值呈线性表达，所以不能描述剪胀率与应力比之间的非线性特征关系。总的来说，本文模型不仅能够良好地描述各阶段和特征状态下的剪胀率变化情况，而且在不同应力路径下对于剪缩型土的剪胀率变化特性均有较强的适应性。

图13 不同应力路径

图14 不同应力路径下的剪胀模型预测与试验值模拟效果

表6 不同应力路径下的剪胀模型预测与实验值的欧式距离

5 剪胀模型的讨论

（1）在一般的剪胀模型中，认为应力比是剪胀率的唯一影响因素。本文通过对大量剪缩型土剪胀性实验数据的特征挖掘，发现剪胀率不仅与应力比有关，还与应变和应力增量有关，这就是一般剪胀模型不合理的根本原因。由各相关性函数综合建立的剪胀模型的拟合度明显高于单个影响因素的拟合度，进一步表明了剪缩型土的剪胀模型仅仅考虑单个因素的影响是远远不够的，必须考虑主要影响因素和附加影响因素的综合作用。

（2）在建立剪胀模型的过程中，考虑到不同土类应力应变关系存在差异，因此在研究剪胀率与各影响因素之间的相关性函数时进行了归一化处理，本文模型也是在剪胀率与各影响因素的相关性函数基础上综合建立的。验证试验结果也表明了本文模型可以较好地反映剪缩型土的剪胀率变化共同规律，所以在研究不同剪缩型土的剪胀性的时候，只需通过归一化的逆处理方法即可反映出不同土类个体的差异和特性，这在4.2节中的多应力路径验证试验中可以体现，这也进一步证明了本文采用的基于大数据技术来建立剪胀模型的方法针对不同类别的剪缩型土具有良好的适用性，所以不会掩盖不同剪缩型土间的差别。

（3）目前来看，相比于常规的试验研究到理论推导的方法，本文是针对剪缩型土在简单应力路径下的剪胀性变化规律研究，对复杂受力情况下的土体表现还尚未建立起系统性的研究方法，这是因为当前在岩土工程领域对大数据技术的研究利用不够深入，尚未建立起系统的试验数据存储库，因此对开展复杂受力条件下的大数据本构关系研究造成了一定的困难。但是随着大数据技术在岩土工程领域的发展，这一问题势必会得到解决，笔者希望本文方法能为土体本构关系的研究开辟出新的道路。

（4）采用大数据技术研究剪缩型土的剪胀性特征，是课题组在土体本构关系与大数据交叉领域中的初步探索，希望能从中获取关于剪胀性的变化规律，加深对土体基本力学特性的认识。本文提出的剪胀模型较合理地考虑了剪胀率各类影响因素的综合作用，虽然得到了参数的一些定性的物理意义，但对于参数更为精确的物理意义，下一步我们还将重点进行研究探索。

6 结论

（1）提出了一种并行化的LM优化回归算法。该算法结合了LM算法的核心思想，并在MapReduce计算框架下解决了剪胀性大数据回归分析时的全局优化性差、收敛性慢、计算效率低的问题。（2）通过大数据深度挖掘技术，揭示了应力、应变以及应力增量对剪缩型土的剪胀性影响的大数据特征。通过本文提出的并行化LM 优化回归算法分别得到了剪胀率与各影响因素之间的相关性函数。根据剪缩型土的基本力学特性，建立了可以良好反映其剪胀特性共同规律的剪胀模型。（3）本文建立的剪胀模型和剪缩型土实验数据的剪胀率拟合度为0.938，明显优于剑桥模型和修正剑桥模型下的剪胀模型，并且还可以较好地反映不同应力路径下本文未统计的实验土样本的剪胀特性。