河流泥沙水文学模型边界条件参数化方法探讨

申红彬，吴保生

（1.华北水利水电大学，河南 郑州 450045；2.北京师范大学 水科学研究院 城市水循环与海绵城市技术北京市重点实验室，北京 100875；3.清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084）

1 研究背景

河流泥沙数学模型主要包括：水文学模型、水动力学模型和水文水动力学模型［1］。其中，水文学模型主要以分析河道实测水文泥沙资料为基础，建立经验关系或概念模型。水文学模型往往因形式简单、方便实用，因而在生产实践中得到了较为广泛的应用。现有水文学模型受参数不确定性影响，经常会面临以下应用问题：（1）延用性问题，即原有河道模型参数是否适用于变化环境；（2）移植性问题，即某河道模型参数能否推广应用于其它河道。水文学模型方法虽然不像传统经典数学物理方程那样具有严密的物理概念与数学推导，但作为对客观世界的另一种描述方式，也应具有一定的物理基础［2-3］。因此，要想发展完善河流泥沙水文学模型就需要解决参数的确定方法以及方程的物理意义问题。

现有河流泥沙水文学模型主要以考虑上站来水含沙量的输沙幂律函数公式：（S为河段出口含沙量，Q、S0分别为河段流量、进口来水含沙量，K为输沙系数，a、b为输沙指数）作为基础方程，系数K与指数a、b主要用以反映河流边界条件的影响。其中，系数K主要与河床前期累积冲淤量有关［4］，指数a、b主要与河槽断面形态、沿程距离等几何因素有关［5-7］。吴保生等［8］在对黄河内蒙古河段淤积计算过程中发现，考虑河床冲淤演变过程中系数K值变化可有效提高河槽淤积量的计算精度，并认为指数a、b值变化实质反映了输沙能力在空间上随河床边界条件的变化，系数K值变化实质反映了输沙能力在时间上随河床边界条件调整的变化。王彦君等［9］进一步考虑了河道年内汛期、非汛期输沙指数a、b的差异。姚文艺等［5］通过模型试验直观反映了黄河下游河道不同萎缩模式（“集中淤槽”与“滩槽并淤”）下输沙指数a、b的调整变化情况。鉴于系数K与指数a、b对输沙与冲淤计算精度的重要影响，不少学者［10-12］试图通过统计回归得到不同河段模型参数（系数K、指数a、b）值。不过，这种分析方法偏于经验，得到不同河段、不同时期内的系数K、指数a、b值变化范围较大，存在一定的不确定性。

本文在分析河流泥沙水文学模型经验关系方程基本内涵的基础上，结合对现有模型参数研究成果的分析比较，提出根据河道边界条件确定模型参数的方法，概括总结河道边界条件参数化的研究途径，并从河道边界条件参数化角度出发，通过方程空间—时间变量变换，分析探讨河流泥沙水文学模型方程的物理意义。

2 参数内涵分析

作为河流泥沙水文学模型的基础方程，考虑上站来水含沙量的输沙幂律函数公式可以表示为［4，12-13］：

式中：S为河段出口断面含沙量，kg/m3；Q为流量，m3/s；S0为河段进口断面来水含沙量，kg/m3；K为输沙系数，与河床前期累计冲淤量有关；a、b为输沙指数，统计表明指数a、b满足：a+b≈1.0［14-16］。

分析河流泥沙水文学模型基础方程式（1），本身蕴含了以下基本内涵：

（1）体现了不平衡输沙的理念。当来水含沙量大于出口含沙量时，河道处于淤积状态；当来水含沙量小于出口含沙量时，河道处于冲刷状态；当来水含沙量等于出口含沙量时，河道处于输沙平衡状态。当河道处于输沙平衡状态时，来水含沙量与出口含沙量应相等于水流挟沙力，则有：

式中S*为河道水流挟沙力，也称临界含沙量。

因指数a、b满足统计关系：a+b≈1.0，相应式（2）中流量指数也可表示为：b/（1-a）≈1.0，这表明式（2）流量指数b/（1-a）具有统计平均意义上的稳定性。

结合式（2），暂时忽略河段沿程流量变化，则基础方程式（1）可表示为其它形式：

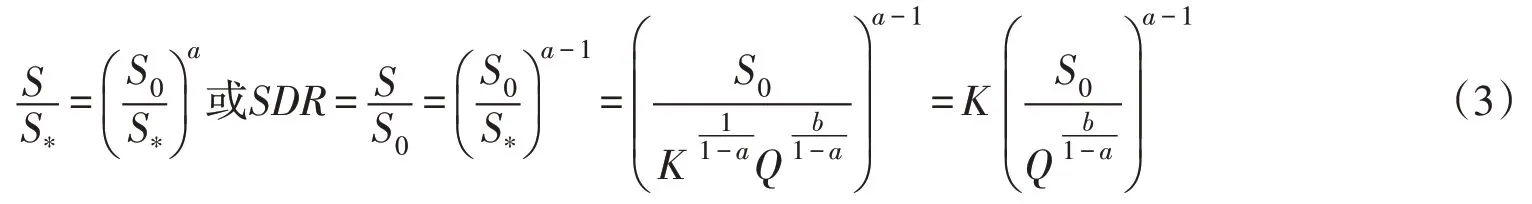
式中：S/S*为河道沿程断面含沙量与临界含沙量的比值；S0/S*为河道进口断面含沙量与临界含沙量的比值；SDR为河段排沙比；S0/Qb/（1-a）为来沙系数。

式（3）左侧公式表明，考虑上站来水含沙量的水沙关系模型实质反映了河道断面含沙量与临界含沙量比值的沿程变化情况。根据不平衡输沙理论，可以判断指数a值应在［0，1］之间，当河道进出口断面距离趋于0时指数a值应等于1.0，当进出口断面距离无穷大时指数a值趋于0［17］。

（2）反映了相对空间的概念。根据模型方程，对于同一出口断面，当上游来水含沙量取不同距离进口断面时，模型参数会有所区别；同理，对于同一进口断面，下游不同距离出口断面的输沙参数也有所不同。假设对于同一河道可以划分为0-1、1-2、…、（n-1）-n共计n个河段，各河段模型参数相同均为K、a、b，则应用模型方程依次递推，可以得到以下关系：

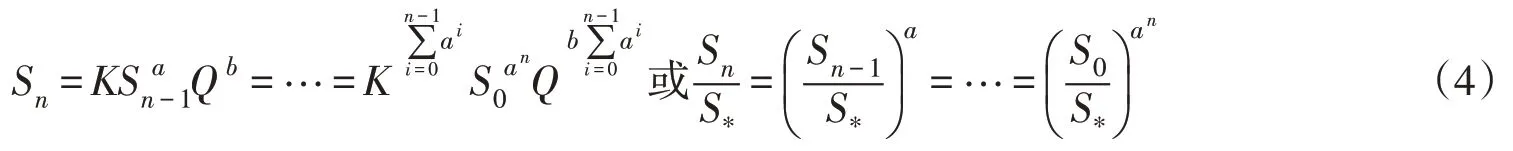
式中：n为河道划分河段数；i为迭代计算序号。

从式（4）可以看出，对于模型方程式（1），同一进口断面下游不同距离出口断面的模型系数、指数是不同的。不过，对于下游每一个出口断面，模型方程系数、指数均具有如下关系：

式（5）表明，对于下游每一个出口断面，河道水流挟沙能力方程式（2）的系数、指数是一致的。

（3）赋予了反映河流自动调整作用的功能。通过建立系数K与河槽累计冲淤量的变化关系，当河道发生累计淤积时，K随累计淤积量的增加而增大；反之当河道发生累计冲刷时，K随累计冲刷量的增加而减小，这实质体现了河槽边界条件调整对输沙能力的影响［8，10，18］：

式中：K0为输沙系数基础值；λ为系数；为前期河床冲淤参数，亿t；ΔWs为计算时段冲淤量，亿t；D为平均冲淤参数，亿t。

综合以上内涵分析可以看出，对于河流泥沙水文学模型基础方程：，模型系数、指数更多受到河道边界条件的影响。所谓河流泥沙水文学模型边界条件参数化方法，就是以河流泥沙水文学模型基础方程为基础，从河道边界条件（如河段长度、宽度、断面形态、河床比降等）参数化角度出发，根据河道边界条件确定模型的系数、指数参数，可表达为如下函数形式：

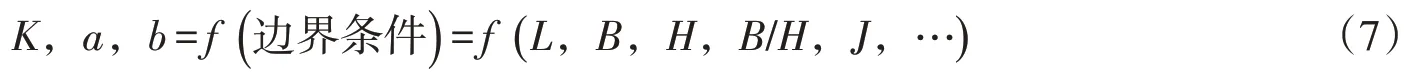
式中L、B、H、J分别为反映河道边界条件的长度、宽度、水深及比降。

3 研究方法途径

3.1 统计分析方法对式（1）两侧取对数，可以得到：

基于式（8），根据河道沿程不同断面实测水沙资料，通过多元线性回归，可以得到不同河段模型参数（系数K与指数a、b）值，进而分析模型参数的变化规律，这就是统计分析方法。

图1为不少研究者基于黄河沿程水文站（图1（a））实测水沙资料统计回归得到的模型参数（系数K与指数a、b）值变化情况（图1（b）），各水文站河段进口断面为上游邻近水文站，具体参见文献［12，19-20］）。不过，因不同河段边界条件相差甚远，且系数K值又与河床前期累积冲淤条件有关，河段选取缺乏统一的标准，导致不同河段模型参数（系数K与指数a、b）变化情况复杂。其中，指数和（a+b）的统计平均值约为1.1，接近于1.0。

根据模型方程内涵（2）的分析，河段选取宜先对同一河段固定同一进口断面，分别选取下游不同距离出口断面，基于实测水沙资料统计回归模型参数。图1（c）为根据式（3）右侧排沙比公式，以黄河下游花园口站为同一进口断面，分别选取下游不同距离出口断面：高村、艾山、利津，简单统计回归河段排沙比与花园口来沙系数之间关系的变化情况（图中：SDRgc、SDRas、SDRlj分别为花园口-高村、花园口-艾山、花园口-利津河段排沙比；Sh/Q为花园口站来沙系数，b/（1-a）≈1.0）。从中可以看出，随着河段距离的增大，模型系数K、指数a的值逐步减小。这为利用统计分析方法直接分析模型参数随距离的变化规律提供了方便。后再对不同河段比较分析距离因子对输沙参数的影响规律。费祥俊等［17］基于黄河下游河道实测水沙资料，通过统计回归，得到艾山至利津、三黑小（三门峡、黑石关、小董）至艾山、三黑小至利津河段排沙比公式（3）指数（a-1）值依次为-0.03、-0.50、-0.53，相应指数a值依次为：0.97、0.50、0.47，显示出河段距离越大指数a值越小的趋势。

鉴于天然河道边界特征沿程变化多样，可基于渠道观测或水槽试验资料，通过统计分析，研究考虑上站来水含沙量的河道水沙关系模型参数（系数K与指数a、b）值的变化规律。例如，图2为长江科学研究院水槽冲刷试验测得的含沙量沿程恢复情况（图2（a））［21］，固定选取某一断面作为进口断面，基于式（3）左侧公式可以率定出下游不同距离出口断面指数a值（图2（b））。可以看出，随着河段出口断面距离的增大，输沙指数a值呈现出明显的衰减趋势。不过，目前对于考虑上站来水含沙量的输沙幂律函数公式，多用于天然河道特别是多沙河流泥沙输移的模拟，较少用于描述渠道或水槽内泥沙的输移。

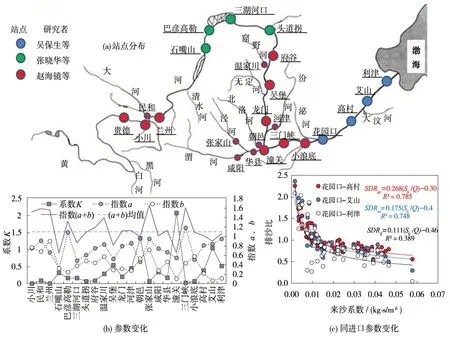
图1 黄河不同河段模型参数统计回归值变化情况

图2 基于水槽试验资料的模型参数统计分析方法

3.2 理论比较途径河流泥沙三类模型（水文学模型、水动力学模型、水文水动力学模型）作为对河流泥沙输移同一物理现象的不同描述，在表达形式上虽存在区别但也存在联系。通过对3类模型开展理论比较分析，可用于探求河流泥沙水文模型参数的计算方法。

在河流泥沙水文水动力学模型中，水流挟沙力方程一般采用基于水流功率理论的简化形式：QS*=QS*=A（QJ）m（A为系数，m为指数，J为比降）［22］。其中，指数m值一般认为在2.0左右，对于不同断面形态河槽指数m值存在一定的区别。比较水流挟沙力方程式（2），两者方程结构形式存在相似性。因此，对于水流挟沙力方程式（2）中的流量指数b/（1-a）值，应等于（m-1）约为1.0左右，这与实测资料统计平均结果相符，而对于系数值K1/（1-a），判断应与河道比降有关。

在水动力学模型中，一维恒定流不平衡输沙微分方程为：

式中：x为沿程距离；ω为泥沙沉速；q为单宽流量；，sb*为河底水流挟沙力，也称为泥沙恢复饱和系数。

根据河流泥沙水文学模型基础方程内涵（1）、（2）的讨论，并参考结合图2，指数a应是一个与输沙距离有关的变量，可以近似采用指数函数进行描述：a=e-κx，相应输沙微分方程可表示为［23］：

式中κ为变化速率参数。

笔者曾对式（9）、式（10）进行比较［23］，通过对Sln（S/S*）在S*附近进行一阶Taylor级数展开，表明Sln（S/S*）与（S-S*）近似相等：

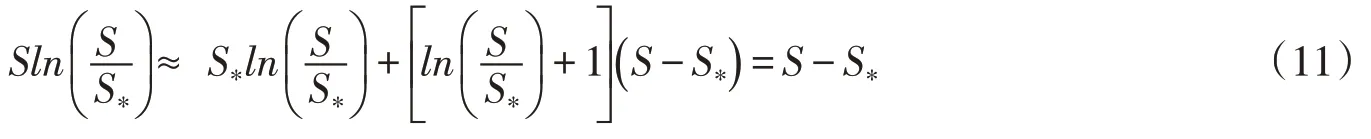
因此，式（10）变化速率参数κ=α*ω/q，相应指数a计算表达式为：

根据式（12），相同流量、比降情况下，不同断面形态河槽下游不同距离断面泥沙水文模型指数a及含沙量沿程变化示意情况如图3所示。

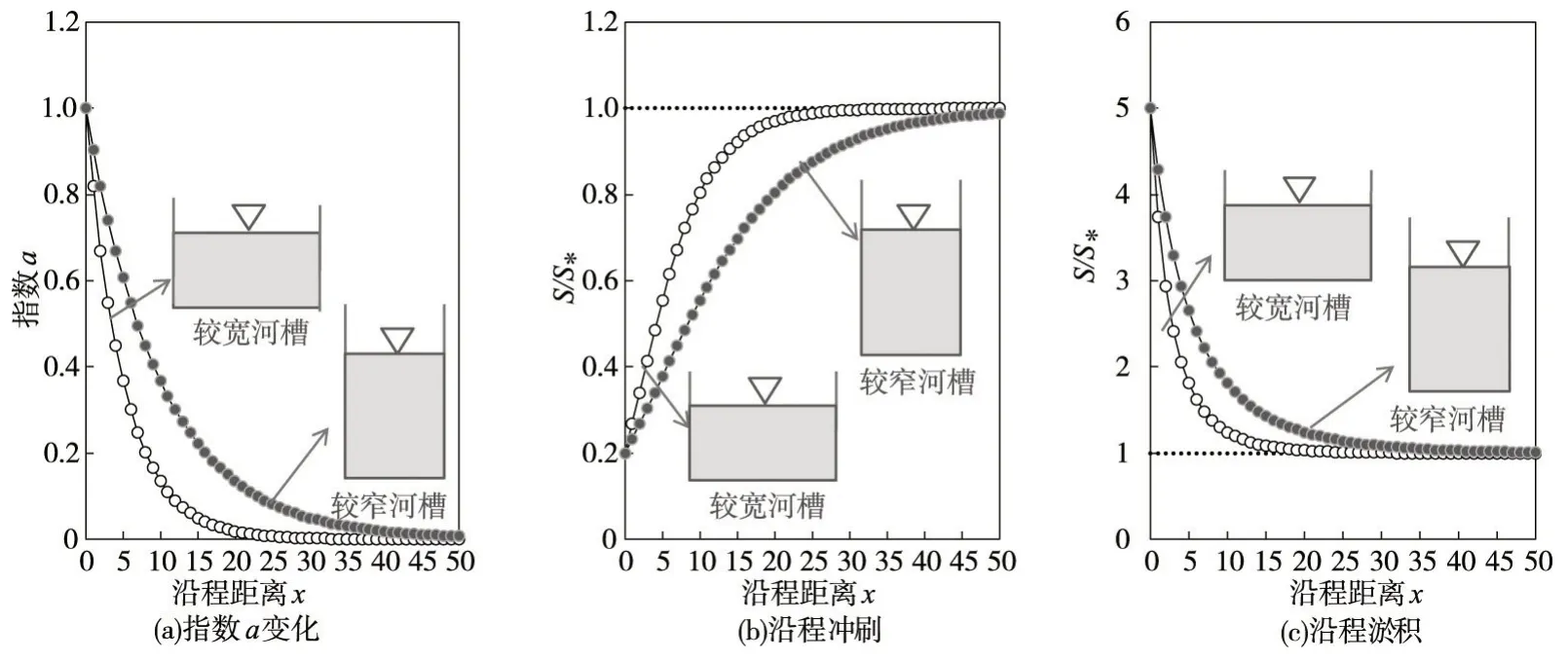
图3 相同流量、比降下不同河宽河槽泥沙水文模型指数a与含沙量沿程变化示意图

基于式（12），输沙微分方程式（10）可进一步表示为：

至于输沙微分方程式（9）与式（10）、式（13）何者描述形式更为合理，尚需后期进一步的研究。

4 方程空时变换

对于一维恒定流，对式（9）、式（13）进行变量变换，令dx=Vdt、q=VH（其中，V为均匀流平均流速，H为平均水深），则二式可以分别变换为：

式（14）、式（15）可以统一表示为如下形式：

式中：y为系统特征变量；t为时间；ye为系统特征变量平衡值；β为变化速率。

因此，从“系统”角度来看，式（14）、式（15）均为系统滞后响应的微分方程，系统特征变量y调整变化速率与该特征变量当前状态y和平衡状态ye之间的差值成正比［24-26］。从断面质点系统跟踪角度来看，式（14）、式（15）描述的是河道水沙质点系统在进口水沙初始条件下，经过一定时间（对应一定运移距离）后，自身水沙组合情况调整并趋向于平衡的过程（见图4），不同之处在于两者对于描述系统水沙组合的特征变量y的选择不同，分别为（S/S*）与ln（S/S*）。

图4 河道断面水沙质点系统滞后响应过程

在一维恒定均匀流情况下，微分方程式（9）的解析解为：

对式（17）进行变量变换，令q=VH，则可以变换为：

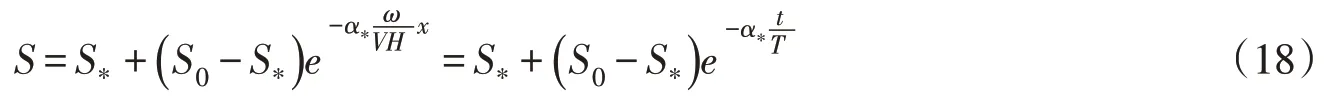
式中：t为时间，t=x/V；T为泥沙沉降时间，T=H/ω。

从式（18）可以看出，以往微分方程式（9）对应的含沙量关于空间变化的解析解，经过变量变换，也可以表示为关于时间变化的滞后响应解的形式。

同理，基于式（12），对于河流泥沙水文学模型方程式（3），经过变量变换也可以表示为：

从式（19）可以看出，原用于确定指数a的河道地貌变量：河长x、河宽B，经变量变换为：河长x、水深H后，再分别与流速V、泥沙沉速ω相除，最终转化为系统自身调整时间t与断面泥沙沉降时间T，这可以从另一角度理解河流泥沙水文模型基础方程的物理意义。

5 结论

（2）河流泥沙水文学模型边界条件参数化研究方法途径主要包括：统计分析方法与理论比较途径。统计分析方法宜先对同一河段选用同一进口断面，分别选取下游不同距离出口断面，基于实测水沙资料统计回归模型参数，进而研究参数随距离变化规律，后再对不同河段比较分析距离因子对输沙参数的影响规律。鉴于天然河道边界特征沿程变化多样，可先选用渠道观测或水槽试验资料，统计分析模型参数的变化规律。理论比较途径主要基于对水文学模型、水动力学模型以及水文水动力学模型三种模型方程的理论比较分析，探求河流泥沙水文学模型参数的计算方法。

（3）从断面质点系统跟踪角度来看，描述河流泥沙运动的水文学与水动力学模型关于空间变化的数学方程形式，经过变量变换均可表示为关于时间变化的滞后响应模型方程形式，两者区别在于对描述系统水沙组合的特征变量选择不同。其中，对于河流泥沙水文模型边界条件参数化的最终结果转化为了水沙质点系统的自身调整时间与断面泥沙沉降时间两个变量，从另一角度提供了对河流泥沙水文学模型基础方程物理意义的理解。