基于AHP-PCA的滚抛磨块评价指标集构建*

杨 雪， 高 炜， 田建艳， 高云松， 杨胜强， 李文辉

(1. 太原理工大学 电气与动力工程学院, 太原 030024) ( 2. 太原理工大学 机械与运载工程学院, 太原 030024) ( 3. 廊坊市北方天宇机电技术有限公司, 河北 廊坊 065000)

机械产品精密化的发展对零件表面质量的要求也越来越高[1]。滚磨光整加工是一项旨在提高零件表面质量的加工技术，其中所用到的磨具统称为滚抛磨块，滚抛磨块是影响零件加工效果和加工效率的关键因素之一[2]。近年来，对磨块及其性能的研究一直是光整加工技术的重点和难点。陈红玲等[3]指出磨块对被加工零件的制造成本有很大的影响，阐述了磨块不同制备方法的优缺点，其中烧结法制备的磨块寿命长、磨削性能好。VIJAYARAGHAVAN等[4]对光整加工中影响能源消耗和材料去除率的输入工艺参数(如零件材料、工艺时间和磨块)进行了研究，表明磨块对能源消耗和材料去除率影响最大。LU等[5]指出磨块在加工中会出现一定的磨损，对被加工零件表面、亚表面质量及表面精度有重要影响；设计了磨削工艺试验，得出了磨损率随时间变化的规律，借助此规律可预测被加工零件表面精度等。郝志明等[6]分析了磨块9项参数对离心式滚磨光整加工过程中平均接触力的影响，结果表明：磨块回弹系数、密度及动摩擦系数对其影响最大。YANG等[7]对滚抛磨块硬度、组织、尺寸等参数进行了研究，结果表明：滚抛磨块的硬度和尺寸对滚磨光整加工效果影响最大。以上学者主要探讨了磨块及磨块部分参数对光整加工过程或效果的影响，但目前有关滚抛磨块参数归纳整理的研究较少。

由于滚抛磨块组成、制备及使用的复杂性，使得其评价指标复杂且繁多，工厂及科研人员的研究也各有侧重，对于滚抛磨块，目前还没有统一的评价指标集。因此，将现有可量化的评价指标归纳，构建了滚抛磨块初始评价指标集。但归纳后的滚抛磨块评价指标集中存在冗余的评价指标，降低了滚抛磨块的评价效率。如何对滚抛磨块评价指标进行筛选整理，建立一套科学合理的评价指标集，对于合理、高效评价滚抛磨块具有重要意义。因此，提出基于层次分析法(analytic hierarchy process, AHP )与主成分分析法( principal component analysis, PCA)构建滚抛磨块评价指标集。

1 滚抛磨块评价指标集的构建

滚磨光整加工过程中，滚筒内的滚抛磨块与零件、滚抛磨块与滚抛磨块之间的碰撞、滚压、磨削等，使得滚抛磨块必须具有组织致密、硬度高、磨削能力强、耐磨损等特性[8]。滚抛磨块评价指标是指能够表征滚抛磨块特性的指标，由这些指标所构成的集合称为滚抛磨块评价指标集。

1.1 滚抛磨块初始评价指标集的构建

通常，评价指标选取的基本原则包括[9]：

(1)反映研究对象的特征；

(2)评价指标来源科学；

(3)评价指标数据具有可获得性。

通过研究滚磨光整加工过程，分析大量滚磨光整加工实际案例及滚抛磨块制备工艺，结合现有滚抛磨块研究文献，得到滚抛磨块初始评价指标集A，如图1所示。

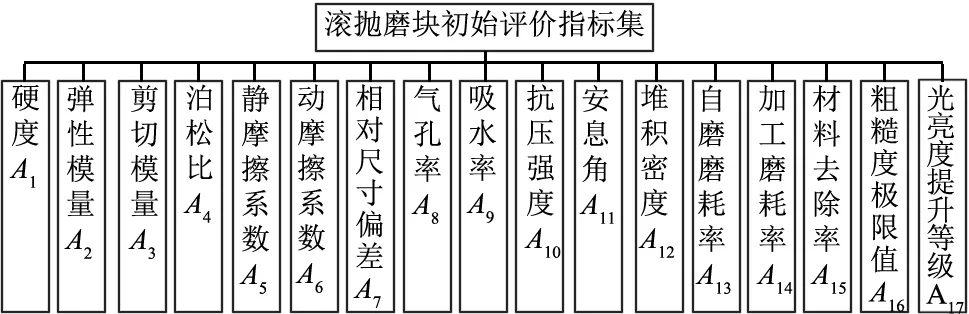
图1 滚抛磨块初始评价指标集

图1中的滚抛磨块初始评价指标集主要包含3类评价指标：(1)与滚抛磨块材料相关的评价指标：硬度、弹性模量、剪切模量、泊松比、静摩擦系数、动摩擦系数与抗压强度；(2)与滚抛磨块制备相关的评价指标：相对尺寸偏差、气孔率与吸水率；(3)与滚抛磨块使用相关的评价指标：安息角、堆积密度、自磨磨耗率、加工磨耗率、材料去除率、粗糙度极限值、光亮度提升等级。

1.2 滚抛磨块评价指标筛选

图1中的初始评价指标集中存在冗余的评价指标，且不同的评价指标对滚抛磨块特性的影响程度不同。评价指标权值可以反映它们的重要程度，故科学的权重确定方法决定了评价指标筛选结果的合理性。现有的权重确定方法分为主观法和客观法，但主观法有较大的人为主观性[10]，客观法又容易忽略实际需求[11]，因此提出将主客观法相结合对滚抛磨块评价指标进行筛选。

1.2.1 基于AHP的滚抛磨块评价指标主观权重计算

AHP常用于评价指标主观权重的确定[12]，它可以依据滚抛磨块制备工艺和滚磨光整加工实际经验对滚抛磨块评价指标相对重要性进行判断决策，从而得到滚抛磨块各评价指标的主观权重。具体步骤如下：

(1)根据专家意见及分析实际加工案例，将滚抛磨块评价指标的重要性按照从大到小的顺序划分为9个等级：①相对尺寸偏差、粗糙度极限值；②抗压强度；③材料去除率；④硬度、自磨磨耗率；⑤静摩擦系数、光亮度提升等级、安息角；⑥弹性模量、剪切模量、泊松比；⑦气孔率；⑧动摩擦系数、加工磨耗率、堆积密度；⑨吸水率。通过引入1～9比率标度[13]对其进行定量化处理，构造滚抛磨块评价指标两两比较判断矩阵T。

(2)计算判断矩阵T的最大特征值及其所对应的特征向量，如式(1)所示。

TP=λmaxP

(1)

式中：T为判断矩阵；λmax为T的最大特征值；P为λmax所对应的特征向量。

(3)按照式(2)、式(3)对判断矩阵进行一致性检验。

(2)

(3)

式中：CR为判断矩阵的随机一致性比率；CI为判断矩阵的一致性指标；RI为判断矩阵平均随机一致性指标；q为判断矩阵的阶数。RI的值如表1所示[14-15]，当矩阵为一阶或二阶时，RI为0。CR≤0.1，即认为判断矩阵构造合理，否则需对判断矩阵做出调整。

表1 平均随机一致性指标值

(4)计算滚抛磨块评价指标主观权重，如式(4)所示。

(4)

式中：wi(i=1,2,…,I)为滚抛磨块第i个评价指标主观权重；Pi为特征向量的第i个分量。

1.2.2 基于PCA的滚抛磨块评价指标客观权重计算

PCA可以将复杂问题转化成易于操作的数学问题[16]。它可以根据主成分负载系数的大小判断评价指标对滚抛磨块性能的影响是否显著。具体步骤如下：

(1)构造滚抛磨块评价指标样本矩阵。

(2)滚抛磨块评价指标原始数据标准化处理。为了消除滚抛磨块评价指标量纲的影响，采用z-score标准化方法[17]对评价指标原始数据进行处理。

(3)主成分表达式。计算标准化后样本矩阵的协方差矩阵、协方差矩阵的特征值及其对应的特征向量，并将特征值按从大到小的顺序进行排列。则主成分表达式如式(5)所示。

Fr=ar1X1+ar2X2+…+arIXI

(5)

式中：Fr(r=1,2,…,R)为第r个主成分；Xi为评价指标经标准化后的值；ari为主成分负载系数，其值对应着第r大特征值的特征向量的第i个分量。

(4)选择主成分。计算第r个主成分的方差贡献率cr，其表示主成分Fr所解释的方差占滚抛磨块评价指标总方差的比重，反映了第r个主成分的重要程度，计算公式如式(6)所示。

(6)

式中：λr为协方差矩阵第r大的特征值。而后计算主成分的累计贡献率，根据累计贡献率大于90%的要求选取主成分[18]。

(5)计算滚抛磨块各评价指标客观权重。根据所选择主成分中指标的信息含量对指标进行加权[19]，则滚抛磨块各评价指标的客观权重计算公式如式(7)所示。

(7)

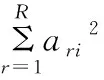
1.2.3 最终滚抛磨块评价指标集

采用加权求和方法计算滚抛磨块各评价指标主客观综合权重，对综合权重小于平均权重的评价指标进行剔除后，所保留的评价指标构成了最终的滚抛磨块评价指标集。

滚抛磨块各评价指标主客观综合权重计算如式(8)所示。

wi*=αwi+(1-α)wi′

(8)

式中：wi*为滚抛磨块初始评价指标集中第i个评价指标主客观综合权重；wi为第i个评价指标主观权重；wi′为第i个评价指标客观权重；α为权重比例系数(0<α<1)。结合大量的试验仿真，取α=0.4。

设最终构建的评价指标集包含M个评价指标，则其中各评价指标的主客观综合权重计算公式如式(9)所示。

(9)

式中：Wm(m=1,2,…M)为最终构建的滚抛磨块评价指标集中第m个评价指标的主客观综合权重；wm*为第m个评价指标在初始评价指标集中的主客观综合权重。

1.3 最终滚抛磨块评价指标集合理性验证方法

为了验证最终所构建的滚抛磨块评价指标集的合理性，分别依据初始及最终的评价指标集对滚抛磨块进行评价。滚抛磨块评价的具体步骤如下：

(1)计算滚抛磨块各评价指标优劣程度：

劣化度用来表征各指标的优劣程度[20]。评价指标值在良好范围内，则其没有劣化，将此时的劣化值定为1；不在良好范围内的评价指标值，其劣化度按照各自建立的劣化模型进行计算。根据滚抛磨块评价指标特点及实际加工经验，建立其各评价指标劣化度计算模型，如图2所示。

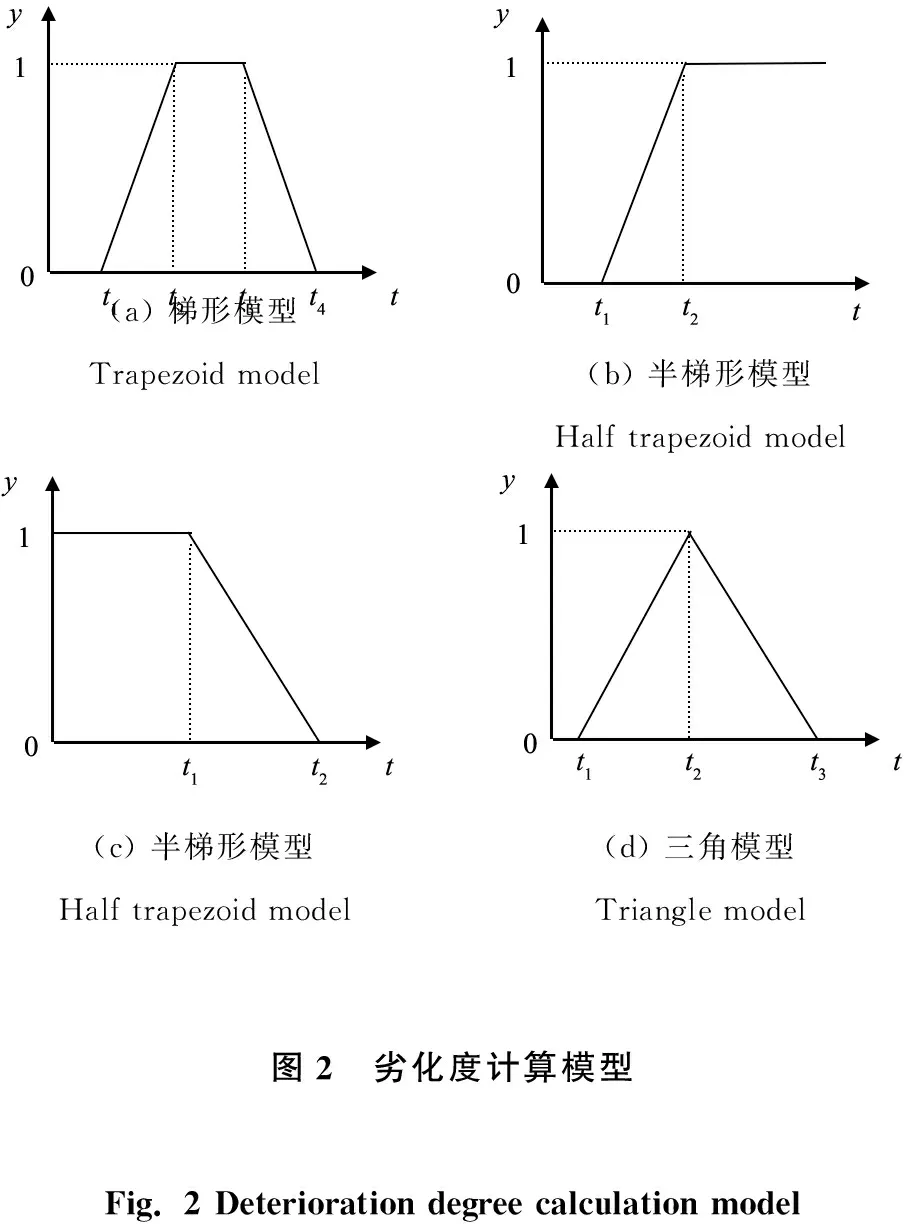
(a) 梯形模型Trapezoid model(b) 半梯形模型Half trapezoid model(c) 半梯形模型Half trapezoid model(d) 三角模型Triangle model图2 劣化度计算模型Fig. 2 Deterioration degree calculation model

图2中y、t分别为滚抛磨块各评价指标的劣化值和优劣阈值。静摩擦系数、动摩擦系数、吸水率、抗压强度、安息角、自磨磨耗率、加工磨耗率及材料去除率的劣化度计算模型如图2a所示，t1、t4为严重异常的阈值，t2、t3为良好范围的阈值；弹性模量、剪切模量、泊松比及光亮度提升等级的劣化度计算模型如图2b所示，t1为严重异常的阈值，t2为良好范围的阈值；相对尺寸偏差、气孔率及粗糙度极限值的劣化度计算模型如图2c所示，t1为良好范围的阈值，t2为严重异常的阈值；硬度和堆积密度的劣化度计算模型如图2d所示，t1、t3为严重异常的阈值，t2为最优值。

(2)计算滚抛磨块评价值

设有N个评价指标，则滚抛磨块批次评价值V的计算公式如式(10)所示。

(10)

式中：Wn′(n=1,2,…N)为滚抛磨块第n个评价指标的主客观综合权重；yn为第n个评价指标的劣化值。评价值越大，滚抛磨块性能越好。

2 试验仿真及结果分析

2.1 滚抛磨块评价指标筛选仿真

采用某工厂26种烧结型球形滚抛磨块各评价指标数据进行了大量的仿真研究，计算了滚抛磨块各评价指标的主观权重与客观权重，根据主客观综合权重对滚抛磨块评价指标进行了筛选。

2.1.1 基于AHP的滚抛磨块评价指标主观权重计算 仿真

首先，构造滚抛磨块两两评价指标比较判断矩阵T；然后根据式(1)计算出判断矩阵的最大特征值λmax=17.675 2；而后根据式(2)计算得到判断矩阵的一致性比率CR=0.026 2<0.1，故可知所构造的判断矩阵通过一致性检验，矩阵构造合理；最后根据式(4)计算可得滚抛磨块初始评价指标集中评价指标A1～A17的主观权重w={0.066 0， 0.028 4， 0.028 4， 0.028 4， 0.043 6， 0.013 4， 0177 9， 0.019 3， 0.009 9， 0.131 4， 0.043 6， 0.013 4， 0.066 0， 0.013 4， 0.095 3， 0.177 9， 0.043 6。

2.1.2 基于PCA的滚抛磨块评价指标客观权重计算 仿真

在主成分分析中，滚抛磨块各评价指标数据所提供的信息量体现在方差上。主成分的方差越大，其方差贡献率越大，该主成分在数据分析时也就越重要。经试验仿真计算，得到各主成分方差贡献率如图3所示，主成分累积贡献率如图4所示。

由图3可以看出：主成分的方差贡献率呈现逐步减小的趋势，说明了主成分的重要程度逐渐降低。由图4可以看出：前4个主成分的累积总贡献率已达到90%以上，说明前4个主成分包含了滚抛磨块初始评价指标集90%以上的评价指标信息，故保留前4个主成分即可。最后，根据式(7)计算可得滚抛磨块初始评价指标集中评价指标A1～A17的客观权重w′={0.044 0， 0.055 6， 0.055 6， 0.055 6， 0.048 4， 0.049 7， 0.057 1， 0.082 6， 0.088 2， 0.054 0， 0.052 5， 0.037 9， 0.077 1， 0.078 0， 0.055 0， 0.037 1， 0.071 6}。

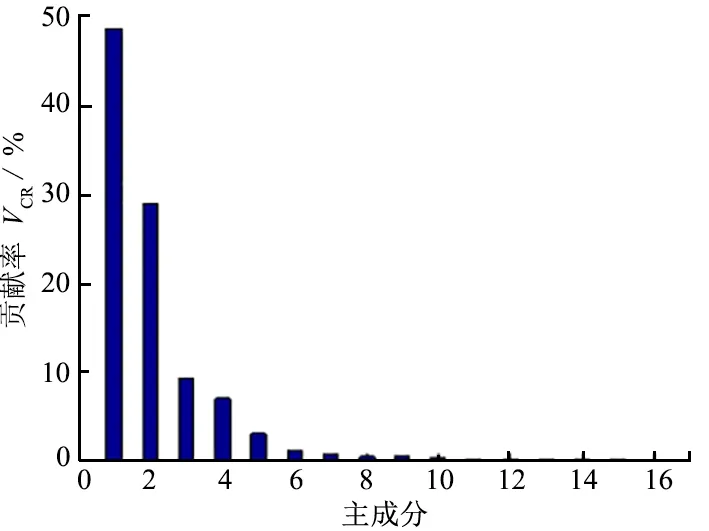
图3 各主成分方差贡献率

图4 主成分累积贡献率

2.1.3 最终滚抛磨块评价指标集计算仿真

根据式(8)计算可得滚抛磨块初始评价指标集中评价指标A1～A17的主客观综合权重w*={0.052 8， 0.044 7， 0.044 7， 0.044 7， 0.046 5， 0.035 2， 0.105 4， 0.057 3， 0.056 9， 0.085 0， 0.048 9， 0.028 1， 0.072 7， 0.052 1， 0.071 1， 0.093 4， 0.060 4}。经计算，滚抛磨块初始评价指标中评价指标的平均权重为0.058 8，故经筛选可得最终的滚抛磨块评价指标集包括：相对尺寸偏差(B1)、抗压强度(B2)、自磨磨耗率(B3)、材料去除率(B4)、粗糙度极限值(B5)以及光亮度提升等级(B6)。

根据式(9)计算可得评价指标B1～B6的主客观综合权重W={0.216 0， 0.174 2， 0.149 0， 0.145 7， 0.191 4， 0.123 8}。

2.2 最终评价指标集合理性验证试验

滚抛磨块合格品是指一批无大面积缺陷和易破碎等质量问题，且能达到相应加工效果的滚抛磨块，否则该批滚抛磨块不合格。采用某工厂φ3FS烧结型球形滚抛磨块20批合格品与20批不合格品的评价指标数据，分别依据滚抛磨块初始评价指标集(A1～A17)及最终所构建的评价指标集(B1～B6)对其进行评价，由于篇幅所限，仅给出部分评价指标数据，如表2所示。

首先，按照1.3节步骤(1)对该工厂以上40批滚抛磨块各评价指标劣化程度进行计算，其中，各评价指标的优劣阈值如表3所示；然后，根据式(10)计算得到以上40批滚抛磨块依据初始及最终评价指标集所计算的评价值分别如图5a、5b所示。

表2 φ3FS烧结型滚抛磨块评价指标数据

表3 φ3FS烧结型滚抛磨块各评价指标优劣阈值

对以上40批滚抛磨块评价指标劣化值进行计算；然后，根据式(10)计算得到以上40批滚抛磨块样品依据初始及最终评价指标集所计算的评价值分别如图5a、5b所示。

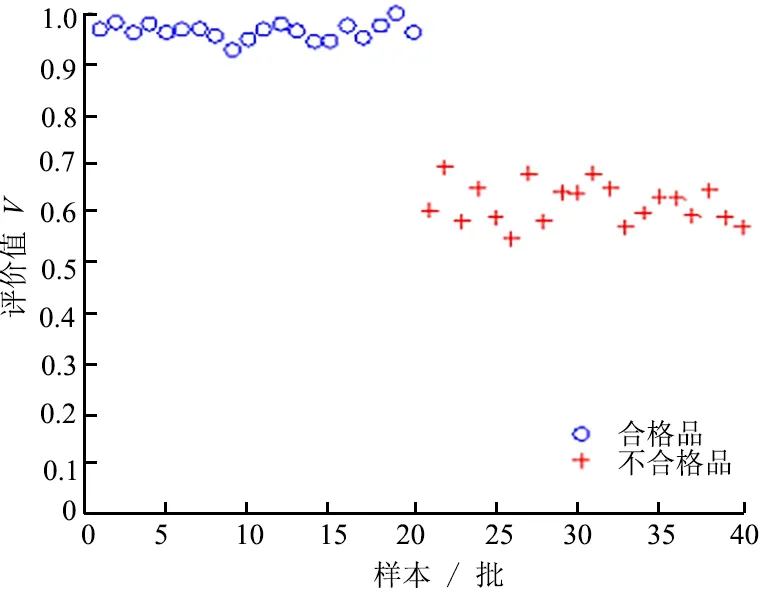
(a) 依据初始评价指标集计算的评价值

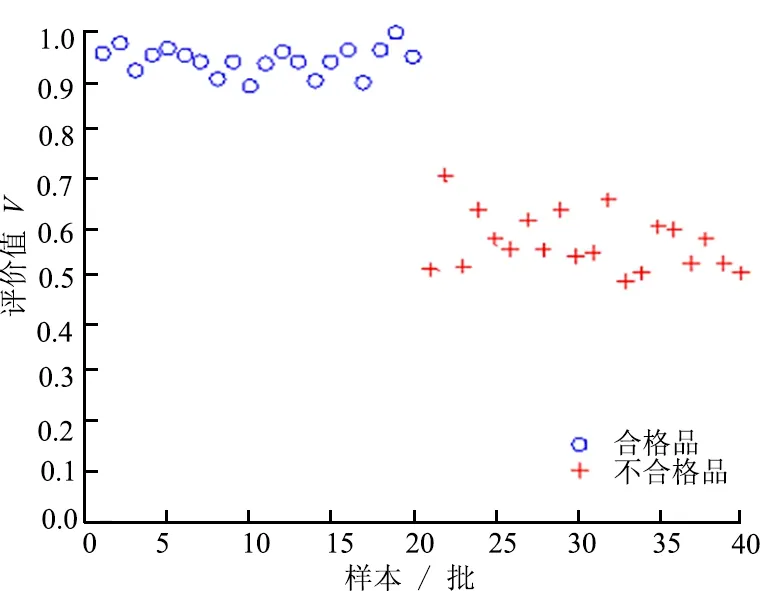
(b) 依据最终评价指标集计算的评价值

由图5a可以看出：依据初始评价指标集计算的20批滚抛磨块合格品评价值均高于0.85，20批不合格品评价值均低于0.70；由图5b可以看出：依据最终评价指标集计算的20批滚抛磨块合格品评价值均高于0.85，20批不合格品评价值仅有一批略高于0.70。对比评价结果可知，依据2种评价指标集对滚抛磨块的评价结果基本一致。

3 结论

为了建立一套科学合理的滚抛磨块评价指标集，首先构建了滚抛磨块初始评价指标集；然后基于AHP与PCA对该集合中的评价指标进行了筛选，构建了最终的评价指标集；最后对比了分别依据初始及最终的评价指标集对滚抛磨块进行评价的结果。试验仿真结果表明，两评价指标集均可对滚抛磨块进行合理的评价，且评价结果基本一致，从而验证了评价指标筛选的合理性，减少了评价指标数据采集的工作量，提高了滚抛磨块的评价效率。