基于广义马尔可夫过程的多部件并联可修复系统稳态可用度分析

孙明明，吴栋，牛建超，解禾，岳龙飞

（1.工业和信息化部电子第五研究所可靠性与环境工程中心，广州 510610；2.航空工业成都飞机工业（集团）有限责任公司技术中心，成都 610092）

引言

可用度是衡量可修复系统可靠性的重要指标。在一个修理工和一个修理设备条件下，对于时齐马尔可夫型的n部件串联及并联可修复系统的可用度解析表达式问题，曹晋华[1]等已经解决这个问题。对于马尔可夫型及非马尔可夫型可修复系统的可用度解析式研究较多，马尔可夫型可修复系统：谢秀梅[2]等研究优先权3部件可修复系统的可用度等指标解析式，Jyotirmoy Sarkar[3]研究考虑备件以及设施保障条件下的单部件系统的可用度解析表达式；非马尔可夫型可修复系统：B.S.Dhillon和A.R.M.Fashandi[4]研究机器人及机器人安全系统的瞬时及稳态可用度解析式，苏保河[5]研究修理工可休假两部件串联可修系统稳态可用度解析式，苏保河[6]研究修理工到系统外工作的n部件串联可修复系统可用度表达式，类似相关研究还有B.S.Dhillon[7]等，Who Kee Chung[8，9]等；还有 Karin S. de Smidt-Destombes等[10，11]、Jyotirmoy Sarkar等[12]、Wei Xie等[13]研究表决系统、Wenqing Wu等[14]均得到系统可用度的解析式。但是，较少研究者对非马尔可夫型可修复系统稳态可用度解析表达式求解进行分析研究，因此值得进行探索研究。

1 基本模型

1.1 问题描述

对于单部件、两部件、三部件的串联及并联的可修复系统研究较多，并且在其部件平均故障间隔时间或修理时间分布不同时为指数分布条件下，得到系统的可用度解析表达式研究成果丰富。

多部件的并联可修复系统，在实际工程中应用广泛。但是较少研究者分析过：在组成系统部件的平均故障间隔时间和故障后修理时间分布不同时为指数分布时，系统可用度的解析表达式。本论文主要考虑修理时间分布为一般连续型时，系统可用度解析表达式。

1.2 模型假设

1）可修复系统由N个同型部件并联构成；

2）部件的平均故障间隔时间分布服从参数相同的指数分布，其参数为λ；部件修理时间分布服从一般连续型分布G(t)，其概率密度为g(t)，

各随机变量相互独立；

3）系统有一个修理设备和一个修理工；

4）故障部件能修复如新；

5）系统中出现一个部件故障就立即对其进行维修，更换修理期间不停机；

6）在更换修理期间，另一部件发生故障，则需要等待更换修理；

7）系统由k到k+1状态故障率为λk，k=0，1，…，n-1。

1.3 系统建模

N(t)=i，若时刻t有i个部件故障，i=0，1，2，…，n。

系统中部件故障规律是：

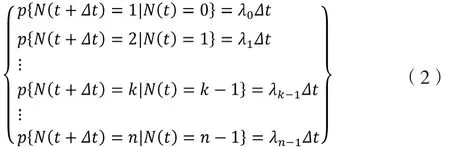
由于修理时间服从一般分布，时刻t以后系统发展概率不仅仅依赖在时刻t有几部件故障，还依赖于正在修理的部件在时刻t以前已经修理过的时间长。引入补充变量X(t)表示时刻t正在修理的部件已经修理过的时间长。过程{N(t)，X(t)；t≥0}为一个连续的广义马尔可夫过程。任意时刻t，给定N(t)，X(t)具体值，则过程{N(t)，X(t)；t≥0}在时刻t以后概率规律与时刻t以前该过程的历史无关。对t≥0，x≥0，令

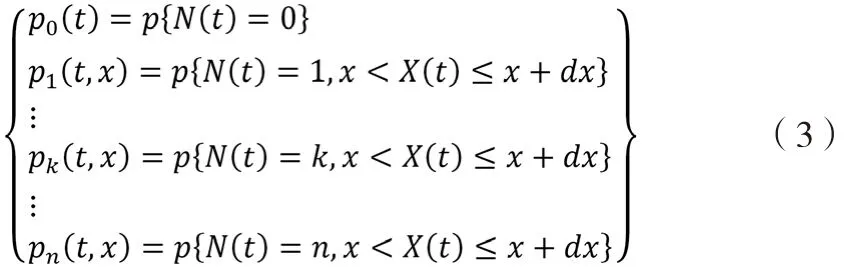
0时刻，各部件均完好，初始条件。

po(0)=1，pk(0，x)=0，k=1，2，…，n，0时刻不发生故障。

由（3）可导出如下方程组：

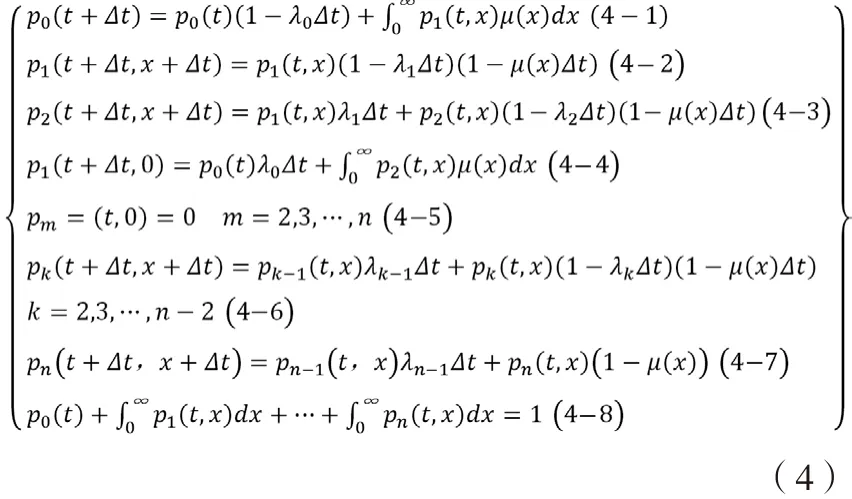
具体推导上述各式：

（4-1）当N(t+Δt)=0，有N(t)=0在 t，t+Δt内部件不发生故障；可以N(t)=1，X(t)=x＞0，在 t，t+Δt故障件更换修理完成。

（4-2）当 N(t+Δt)=1，X(t+Δt)=x+Δt，x＞0，有N(t)=1，X(t)=x＞0，在t，t+Δt内未产生新的故障件，同时更换修理的故障件未修好。

（4-3）当 N(t+Δt)=2，X(t+Δt)=x+Δt，x＞0，有N(t)=1，X(t)=x＞0在 t，t+Δt内修理更换故障件时，产生新的故障件；有N(t)=2，X(t)=x＞0在 t，t+Δt内正在修理更换的故障件未修好，同时未产生新的故障件；有N(t)=3，X(t)=x＞0，在t，t+Δt内恰好更换修理好故障件，到N(t)=2，X(t)=0，即在等待更换维修的故障件，还未开始更换维修，和假设条件故障立即维修相互矛盾，即N(t)=2和X(t)=0不能共存。

（4-4）当N(t+Δt)=1，0≤X(t+Δt)≤Δt，刚刚开始维修，但还未更换维修，有N(t)=0，在t，t+Δt内恰发生一个故障件，需要更换维修；N(t)=2，X(t)=x＞0，t，t+Δt在内恰好有一个故障件更换维修完成，而另外一个等待更换维修的故障件还未开始更换维修。

（4-5）N(t)=m≥2，X(t)=0不共存，与假设条件故障立即维修相互矛盾，pm=(t，0)=0，m=2，3，…，n。

（4-6）与（4-3）同理可得。

（4-7）当 N(t+Δt)=n，X(t+Δt)=x+Δt，x＞0，有N(t)=n-1，X(t)=x＞0在t，t+Δt内正在更换维修的过程中，又有新的故障件发生；N(t)=n，X(t)=x＞0在t，t+Δt内正在更换维修，故障件但是未未修好。

（4-8）全概率公式可得。

对方程式（4）变换得：

对（5）进行拉普拉斯变换得：

对（6-2）微分方程进行求解得：

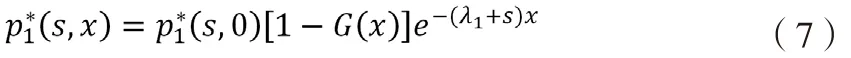
将（7）式代入（6-1）式得：

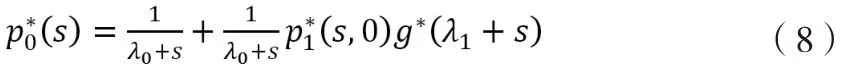
将（7）代入（6-3）式得：

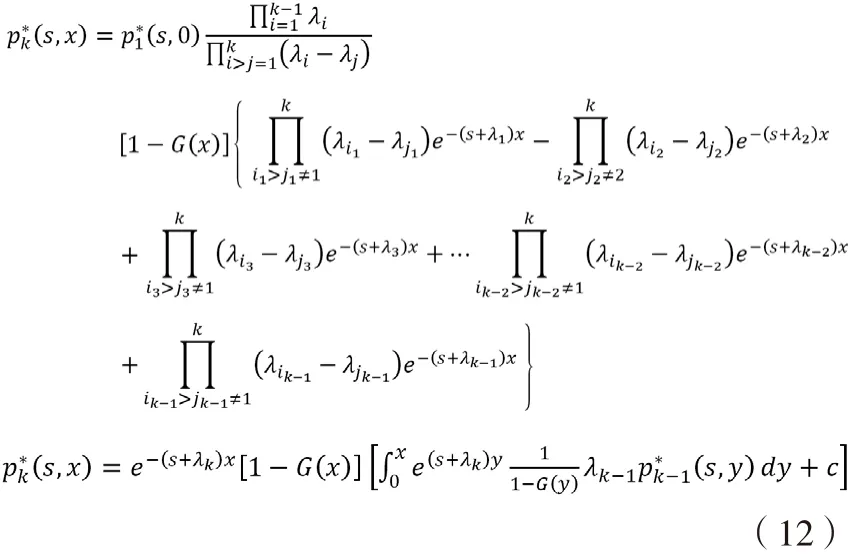
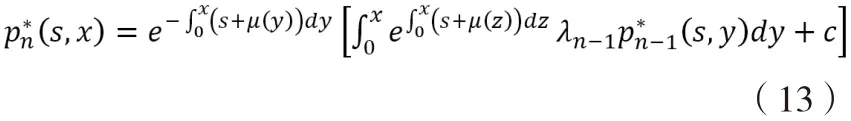
1.4 系统可用度

则系统稳态可用度，由阿贝尔定理[1]可知

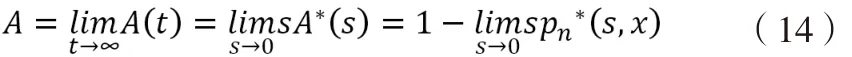
2 结论及展望

本文主要是对于多部件并联可修复系统稳态可用度进行研究，推导出基于广义马尔可夫过程中该系统任意状态概率通用解析式；基于阿贝尔定理并得到基于广义马尔可夫过程该系统稳态可用度解析表达式。可以对于具有工程意义的表决系统进行研究，基本思路相类似。由于本文研究可修复系统的部件平均故障间隔时间服从指数分布、部件更换修理时间服从一般分布，如果该系统部件的平均故障间隔时间、部件更换修理时间均服从一般分布，分析该系统稳态可用度，则必须对该系统偏微分方程组解的适定性和稳定性进行分析研究，可进一步运用C0

-半群理论、不动点理论或者Volterra方程理论进行进一步探索分析。