新高考形势下的立体几何教学感陪

徐冲 刘烨烨

摘要：本文从学生立体几何空间想象能力及作图能力的培养，特殊几何模型的应用，立体几何与古代文化三个方面阐述在2021届新高考形势下立体几何的一些教学策略与感悟。

关键词：立体几何;策略;感悟

一、空间想想象能力以及作圈能力的培养

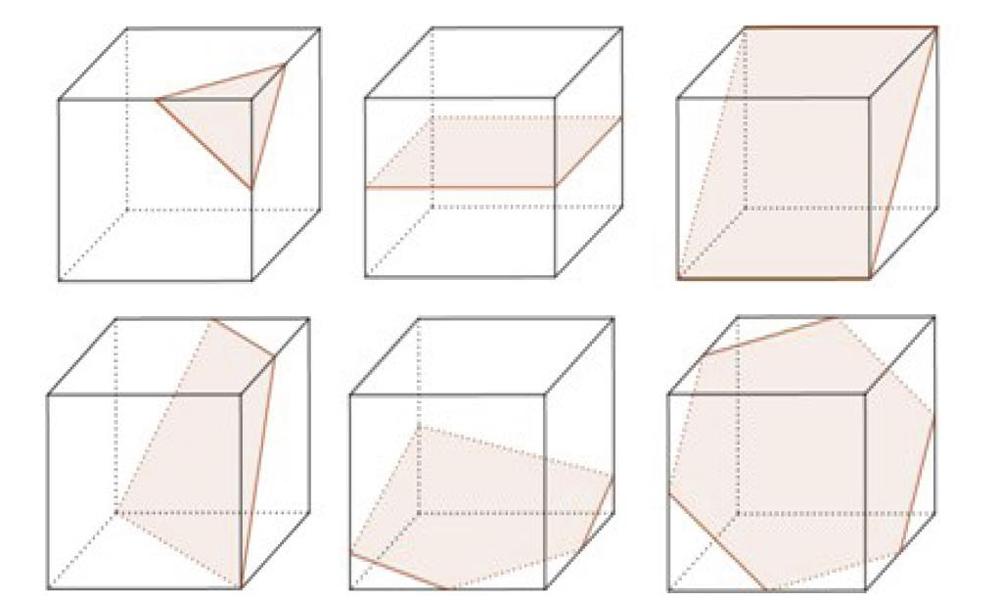
立体几何的知识结构特点要求学生必须具备一定的空间想象能力以及作图能力，否则不可能真正地学好和应用这部分知识，许多高中生对立体几何这一章节“望而却步”，最根本的原因就是缺乏空间想象能力以及作图能力。立体几何最开始的教学重点应该是帮助学生逐步形成空间观念，先让学生了解各种空间几何体，直观地感受立体图形，在接触足够多的立体图形后再深入探究空间几何体的内部结构，探究其中点，线，面的关系。教师应遵循从整体了解空间几何体到局部探究各几何体的内部结构，也要遵循从具体实物到抽象几何关系的原则。在立体几何的教学过程中教师应该向学生提供丰富的实物模型或利用几何画板，利用GGB等多媒体软件向学生展示空间几何体，这样可以帮助学生非常直观、方便地认识空间几何体的图形结构特征，为学生深入学习图形点线面的几何性质提供依据，强调几何学习的直观性，经历这样的过程也有助于学生进一步掌握在平面上表示空间图形的方法和技能，同时有助于培养学生在平面上作空间图形的能力。新课程标准中给了这样一个案例：正方体截面的探究情境：如果我们用一个平面去截切一个正方体，那么所得的截面的形状将会是什么样的？我们可以先对剖面进行分类，可以找到一种方法来切出这些剖面，并描绘这些剖面的演示图。比方说，可以根据横截面图中的边数来分。

1.如果正方体被截得的截面是三角形，能够截切出多少个不同的三角形？

2.如果截面是四边形，能够截切出多少不同的四边形？

3.能否截出五边形，六边形？

4.可以超过六边形吗？

5.截面面积最大的三角形是什么形状的三角形？

引用课标分析：“可以通过切割正方体白萝卜启发思考进行观察白萝卜的截面，或者使用橡皮泥做模型;也可以在透明的立方体小箱中注入彩色水，观察水箱不停变换位置时液体表面的形状，同时加入不同水量时观察表面的形状;我们还可以借助ggb，几何画板等多谋体技术直观、快捷地展示各种可能出现的截切面。这样一个展示的过程是先给学生一些直观的感受，学生一旦有了这些直观感，就可以做出大胆而合理的猜想，然后严谨地证明结论。经历这样逐渐深入，由浅入深，由直观感受到抽象概括的探究过程有助于学生在具体情境中提升直观想象，数学抽象，逻辑推理等素养，从而积累数学探究活动经验。

感悟：新课标，新高考将学生的空间想象力的培养放在十分重要的位置，在平时的教学过程中教师可以借助各种实物，多媒体等工具帮助学生从直观感受开始建立学生的空间想象力和空间作图能力。

二、立体几何与古代文化

2017年全国高中数学学科课程标准第一次明确提出在高考数学中考查数学文化的知识。近年来高考真题卷和模拟卷经常出现以经典的数学经典著作《九章算术》为参考背景的题目，其中2019由国家命题中心命题的山东高三数学模拟卷中也有类似题型。将知识、方法和文化与数学结合起来，并深层次地考虑到学生对新环境，新情境下的知识的理解以及他们将知识在不同的情境背景下的迁移能力。教師教授立体几何这一章节时应做好这方面的融合工作。这里有一些具体的例子，教学过程中可以引用。

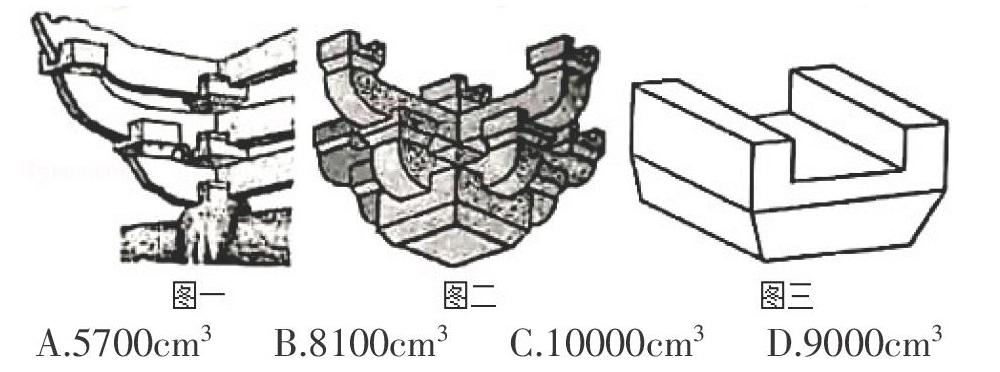
例1.斗拱是中国古典建筑最富装饰性的构件之一，并为中国所特有.图一图二是斗拱实物图，图三是斗拱构件之一的“斗”的几何体.本图中的斗是由棱台与长方体形凹槽（长方体去掉一个小长方体）组成.若棱台两底面面积分别是400cm²，900cm²，高为9cm，长方体形凹橹的体积为4300cm3，那么这个斗的体积是（）。

A.5700cm³B.8100cm³C.10000cm³D.9000cm³

点评：本题以古代建筑为背景，由现实情境抽象出数学问题，考察学生在新情境下处理数学问题的能力。

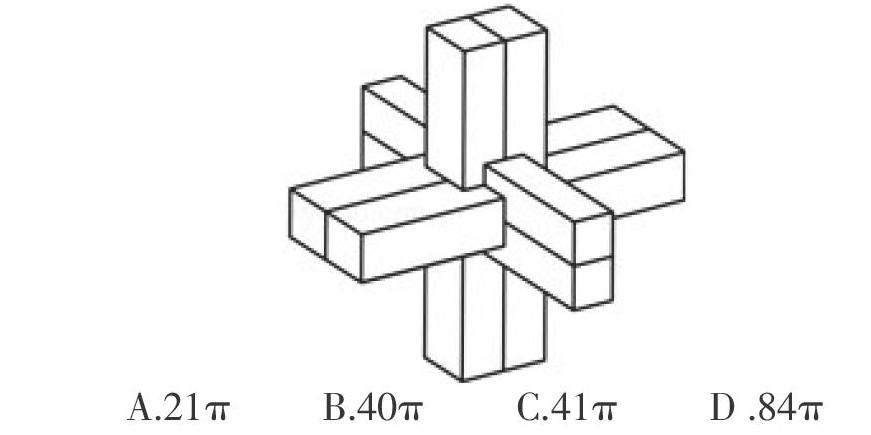
例2.鲁班锁是我们古代的益智玩具，是汉代第一次在所谓的建筑结构中出现的榫卯结构。从外面看，这是一个完全对称的立体图形。从外部来看，六个等长的长方体被分为三组，两两垂直。在图中，如果长方体的高度是8，而底部的方形的边长是2，则将鲁班锁现在放在球形容器中，球容器的最小表面面积是（ ）（容器壁厚度可不计算在内）。

A.21π B.40π C.41π D.84π

点评：本题以古代工具鲁班锁为背景，考察球体表面积问题。新情境蕴含老问题。

例3.中国古代建筑用榫头，卯眼连接木构件。如下图有凸出部分的称之为榫头，相对应的带有凹进部分的叫卯眼，则下图的木质结构可以结合成一个长方体的卯眼的木构件的俯视图可以是（ ）。

点评：以古代建筑为背景，考察了学生的空间想象能力

A.1 B.2 C.3 D.4

点评：试题以《九章算术》中研究立体几何所用的两个特殊椎体（阳马，鳖懦）为背景，给予新定义，增添了试题的新颖性。但其实质仍然考察了线面垂直，面面垂直等基本几何问题。

感悟：以上例题通过古典建筑，榫卯结构，阳马，鳖臑，印信等有关古代文化的物体作为背景，通过现卖情境，让学生感受数学文化的博大精深，在文化中学习数学，在数学中体会中国文化。

三、巧妙使用长方体模型

长方体是特殊的六面体，是众多几何体的基本结构，其特殊性在于其拥有非常好的对称性，各点、线、面元素之间具有相等，平行，垂直等特殊的数量和位置关系，内涵丰富，是研究线面关系，线线关系，面面关系特殊几何体的一个重要载体。在处理某些复杂立体几何问题时，若能根据题意合理、恰当地构造出长方体模型，则可化繁为简，化难为易，巧妙地将题目解出，收到事半功倍的效果。

例1：正四面体的边长为2，则其外接球的体积为__。

点评：将正四面体放入正方体体中，此时比较困难的四面体的外接球问题就转化为正方体外接球问题了。起到了化繁为简的目的。

例2.是正方形平面，，则与所成角的度数是__。

点评：按照题目要求，构造下图的正方体，题目迎刃而解。

例3.正四面体S-ABC，如果E，F分别为SC，AB的中点，那么异面直线EF与SA所成的角为__。

点评：此题看似复杂，但只要将四面体放入下图的正方体中，即可化难为易。

例4.如果四面体的每一个面均是边长为的全等三角形，那么这个四面体的体积是__。

评论：这个四棱锥的对边是相等的，因此可以把六条边作为六个面的对角线来构造一个长方体，四面体的体积问题可以转化为长方体的体积问题。

例5.正四面体中，是的中点，是棱上的一动点，的最小值为，则该四面体内切球的体积为__。

点评：构造下图的正方体，建立空间直角坐标系会非常轻松解决这道题目。

感悟：乱花渐欲迷人眼，有时很多复杂的几何体让我们无从下手，但静下心去看出它本质的出处，会发现很多都源于长方体中，所以利用好长方体模型将会为我们的解题带来很大的方便。

四、结语

立体几何中存在的教学内容属于高中数学教学中的难点和重点，并且对学生未来发展具有重要意义。所以我们在教学中应尽力激发学生学习立体几何的兴趣，培养学生的空间想象能力、作图能力，为学生后续的学习工作奠定基础。