受硫酸盐腐蚀的锈蚀型钢混凝土梁抗弯刚度研究

王艺霖, 张忠和, 刘巧玲

(1.山东建筑大学土木工程学院， 济南 250101;2.建筑结构加固改造与地下空间工程教育部重点实验室, 济南 250101)

引 言

型钢混凝土结构作为钢筋混凝土结构与钢结构的综合改良体，具有承载力高、刚度大、抗震性能好等优点，在重要结构、超高层结构等工程中得到了日益广泛的应用[1-2]。从20世纪80年代开始，学者们就对型钢混凝土结构展开了全面的研究，内容包括实腹式、空腹式的各种梁、柱、节点构件和框架子结构等。2001年，《型钢混凝土组合结构技术规程》(JGJ138-2001)发布，集成了型钢混凝土结构构件的设计方法、构造要求、节点设计、施工要求等[3]。2016年，《组合结构设计规范》(JGJ138-2016)成为了新的行业标准[4]。

为了确保型钢混凝土结构在各种自然条件下的长期正常使用，需要同时满足安全性、适用性、耐久性三方面的功能要求，目前有关安全性的研究比较多[5-7]。另外，与钢筋混凝土结构类似，混凝土内部的型钢也容易在各种内外因素的作用下发生锈蚀，导致耐久性出现问题。对于发生型钢锈蚀的构件，哈娜[8-9]研究了锈蚀后型钢混凝土梁抗弯承载力的随机性并建立了计算公式；朱童[10]研究了型钢锈蚀量的计算模型以及锈蚀量与主要影响因素之间的关系；卢元鹏[11]研究了锈蚀型钢混凝土梁的界面滑移量计算公式并进行了弹性求解；王倩[12-13]用有限元软件模拟了下翼缘发生均匀锈蚀的型钢混凝土梁的力学性能等。

但值得注意的是，耐久性不良之后的型钢混凝土梁，往往也会导致变形程度、裂缝宽度的加大，影响到适用性问题。同时，目前的耐久性研究主要针对的都是型钢发生锈蚀的情况，对于处于硫酸盐环境(如海洋环境)中的型钢混凝土梁，混凝土还可能受到硫酸盐的腐蚀[14-16]，这方面的研究比较欠缺。

为此，本文将考虑型钢锈蚀与硫酸盐腐蚀的耦合效应，对于同时出现型钢锈蚀、混凝土受硫酸盐腐蚀的型钢混凝土梁，从抗弯刚度方面探索其性能劣化规律，建立相关的刚度分析与计算方法，为梁的适用性设计与分析提供依据。

1 试验基本情况

1.1 试验梁的设计与制作

为了探讨锈蚀及硫酸盐腐蚀引起变化的规律，本文设计了四根试验梁：

(1)参照梁：采用C30混凝土，梁长2000 mm，型钢为100 mm×100 mm×6 mm×8 mm的H型钢(屈服强度270 MPa)，在截面内居中布置。纵筋采用4根直径14 mm的HRB400钢筋，箍筋采用直径6 mm、间距150 mm的HPB300钢筋(图1)。型钢的保护层厚度为75 mm，纵筋的保护层厚度为25 mm。

图1 试验梁的型钢、纵筋和箍筋

(2)1号、2号、3号梁：均为出现型钢锈蚀、混凝土受硫酸盐腐蚀的型钢混凝土梁，硫酸根离子浓度和型钢锈蚀程度的控制参数见表1。

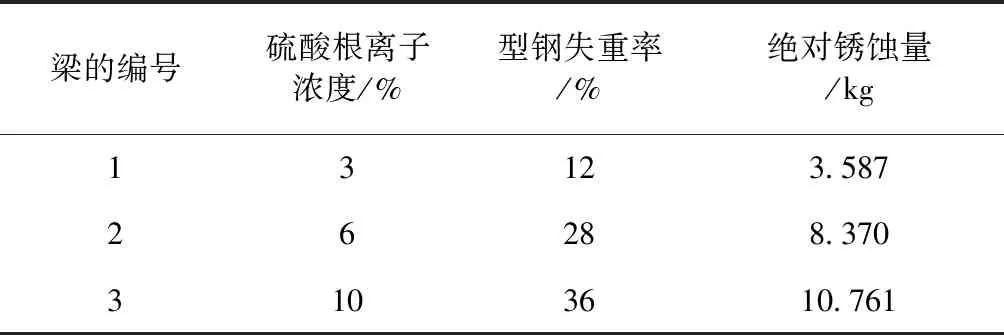
表1 型钢锈蚀程度和硫酸根离子浓度的控制参数

对1～3号梁，直接在搅拌混凝土时掺入硫酸钠作为硫酸根离子。型钢的快速锈蚀采用通直流电的方法来实现，施加不同的通电量以对应相应的锈蚀程度。为了对型钢进行通电锈蚀，需在梁内预埋导线，从型钢上引出来(图2)。待型钢混凝土梁达到28 d龄期后浸入氢氧化钠溶液内开始通电(图3)。

图2 型钢上引出来的预埋导线

图3 浸泡在氢氧化钠溶液内的试验梁

1.2 加载与数据采集方案

待各型钢混凝土梁达到3 M(3个月)龄期后开始加载。加载时，各梁的加载净跨均为1800 mm，通过分配梁在距梁两端支座500 mm处形成两个集中荷载，在中间形成800 mm的纯弯段。因此，弯矩M与加载值F的定量关系为：M=F×500 mm。同时在各梁的纯弯段的中心和两个边界处布置挠度测点(图4)，用全自动位移计进行挠度数据的采集(图5)。

图4 挠度测点的布置

图5 挠度数据的采集

2 受弯变形性能的试验情况及分析

2.1 试验情况

2.1.1 参照梁

(1)跨中挠度值与所加荷载的关系曲线(简称为跨中挠度-荷载曲线)

参照梁的跨中挠度-荷载曲线如图6所示。

图6 参照梁的跨中挠度-荷载曲线

由图6可见：

(a)在加载值≤180 kN(约70%极限荷载)时，跨中挠度都呈明显的线性增长趋势；加载值在180 kN～200 kN(约70%～80%极限荷载)之间时，挠度的增长速度逐渐高于荷载的增长速度；加载值超过200 kN(约80%极限荷载)后，挠度的增长速度显著地高于荷载的增长速度，这表明梁的下部配筋已屈服，同时也说明型钢混凝土梁有较好的延性。

(b)梁最终出现受压区混凝土的压溃。对应的极限荷载为246.6 kN。跨中处对应于极限荷载的极限挠度值为29.11 mm。

(c)型钢混凝土梁的塑性变形能力(或后期变形能力)即称之为延性，通常以挠度的比值βf=fu/fy来表示，称为延性比。其中，fy是指构件屈服荷载对应的挠度或构件的变形发生明显转折时的挠度，fu是指构件达到极限强度时的挠度(即极限挠度)。据此可算得参照梁的“延性比”βf为3.75。

(2)纯弯段的中心及两个边界点的挠度值与所加荷载的关系曲线(简称为挠曲线)

参照梁的挠曲线如图7所示，基本呈抛物线形状。

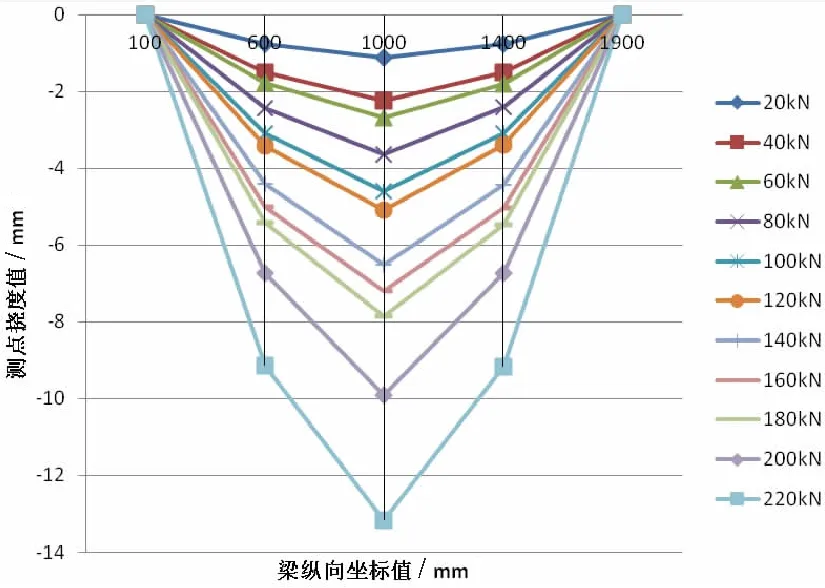
图7 参照梁的挠曲线

2.1.2 1号梁

(1)跨中挠度-荷载曲线

1号梁的跨中挠度-荷载曲线如图8所示。

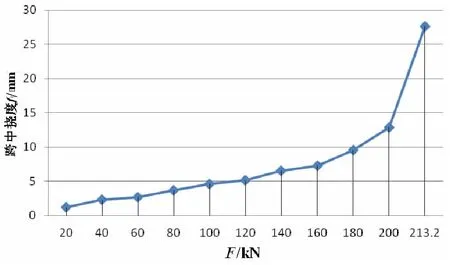
图8 1号梁的跨中挠度-荷载曲线

由图8可见，跨中挠度-荷载关系曲线在加载前期也基本呈线性增长，但当加载值超过160 kN(约75%极限荷载)后转为非线性增长。梁最终也出现受压区混凝土的压溃，对应的极限荷载为213.2 kN。跨中处对应于极限荷载的极限挠度值为27.63 mm，计算得到延性比βf为3.80。

(2)挠曲线

1号梁的挠曲线如图9所示，也基本呈抛物线形状。

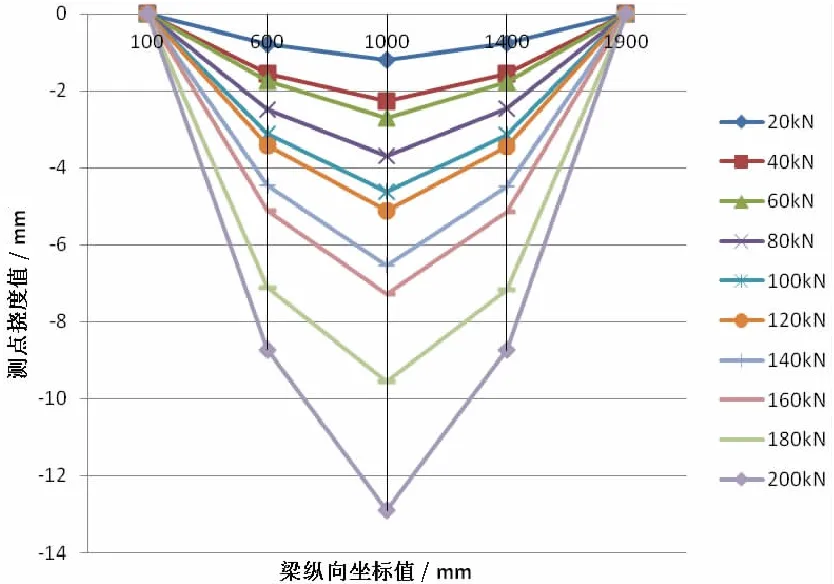
图9 1号梁的挠曲线

2.1.3 2号梁

(1)跨中挠度-荷载曲线

2号梁的跨中挠度-荷载曲线如图10所示：

图10 2号梁的跨中挠度-荷载曲线

由图10可见，跨中挠度-荷载关系曲线的线性增长段很短，在60 kN(约极限荷载35%)后，挠度的增长就转入非线性阶段。梁最终也出现受压区混凝土的压溃，对应的极限荷载为164.6 kN。跨中处对应于极限荷载的极限挠度值为21.13 mm，计算得到延性比βf为4.82。

2)挠曲线

2号梁的挠曲线如图11所示，也基本呈抛物线形状。

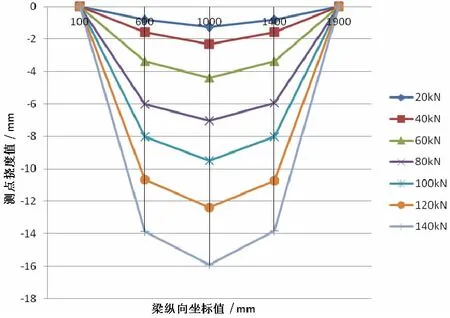
图11 2号梁的挠曲线

2.1.4 3号梁

(1)跨中挠度-荷载曲线

3号梁的跨中挠度-荷载曲线如图12所示：

图12 3号梁的跨中挠度-荷载曲线

由图12可见，跨中挠度-荷载关系曲线没有明显的线性增长段，说明构件在40 kN(约极限荷载39%)后，挠度的增长就转入非线性阶段。梁最终也出现受压区混凝土的压溃，对应的极限荷载为103.2 kN。跨中处对应于极限荷载的极限挠度值为17.86 mm，计算得到的延性比βf为5.95。

(2)挠曲线

3号梁的挠曲线如图13所示，也基本呈抛物线形状。

图13 3号梁的挠曲线

2.2 规律小结及原因分析

(1)从参照梁到3号梁，跨中挠度-荷载曲线的非线性段不断提前出现。进入非线性阶段后，各测点(包含跨中处和纯弯段的两个边界点)的挠度增长量与荷载增长量都不再呈线性关系，而且比值越来越大。荷载达到160 kN后，1号梁的各测点挠度值开始明显高于参照梁；荷载达到60 kN后，2号梁的各测点挠度值开始明显高于1号梁；荷载达到40 kN后，3号梁的各测点挠度值开始明显高于2号梁。

主要原因：锈蚀会导致型钢屈服强度的下降，随着锈蚀程度的不断加深，梁内型钢的屈服阶段不断提前。型钢一旦发生屈服，会在较小的拉应力增量(对应于弯矩增量，即加载值的增量)下就发生较大的拉伸量(对应于跨中挠度值的增加)，使得跨中挠度-荷载的关系转入非线性阶段。因此，型钢锈蚀程度的加深对应着跨中挠度-荷载曲线非线性段临界点的不断提前。进入非线性阶段后，抗弯刚度是趋于下降的，意味着同样的荷载增长量，对应着更大的挠度增长量。

(2)从参照梁到3号梁，跨中处的极限挠度值不断下降，见表2。

表2 各梁跨中处的极限挠度值

同时，1号梁跨中处在达到极限挠度时，其极限挠度明显大于参照梁在同样荷载作用下的挠度；2号梁跨中处在达到极限挠度时，其极限挠度明显大于1号梁在同样荷载作用下的挠度；3号梁跨中处在达到极限挠度时，其极限挠度明显大于2号梁在同样荷载作用下的挠度。

主要原因：从参照梁到3号梁，极限荷载下降显著；同时，由于型钢锈蚀和混凝土腐蚀程度的加深，在同样荷载的作用下，梁的变形会增大，意味着梁的抗弯刚度也有所下降。

3)从参照梁到3号梁，延性比不断增大，见表3，表明延性不断提高。

表3 各梁跨中处的延性比βf

主要原因：型钢锈蚀和混凝土腐蚀程度的加深导致梁越来越早地进入塑性阶段，其极限变形能力与弹性阶段变形能力的比值则越来越大。

3 受硫酸盐腐蚀的锈蚀型钢混凝土梁的抗弯刚度分析及计算方法

由于适用性的要求，实际工程中的型钢混凝土梁一般都要处于弹性工作阶段。由图8、图10和图12的跨中挠度-荷载关系曲线可知，1～3号梁在弹性阶段的跨中挠度-荷载关系为线性关系，存在一个相对稳定的弹性抗弯刚度值，可用于各种变形相关的计算。下面分析一下弹性抗弯刚度的取值问题：

说明：本研究针对的是3 M龄期的梁，因此没有考虑荷载的长期效应(混凝土收缩、徐变、塑性发展等)，这里只对短期抗弯刚度(记为Bs)进行分析。

对于型钢混凝土梁，“最小刚度原则”仍然成立：在全跨长范围内，都可按弯矩最大处的截面弯曲刚度(亦即按最小的截面弯曲刚度)，用材料力学/结构力学方法中不考虑剪切变形影响的公式来计算挠度[17]。据此，可基于各级荷载作用下的跨中挠度值来确定Bs的数值。

具体来说，对于三分点处作用集中荷载的简支梁，记跨度l(=1.8 m)，加载值F对应产生的跨中挠度值为Δ，则根据虚功原理可得：

(1)

进而得：

(2)

然后结合图8、图10、图12中的跨中挠度-荷载数据和式(2)，可获得1～3号梁的Bs值，见表4。

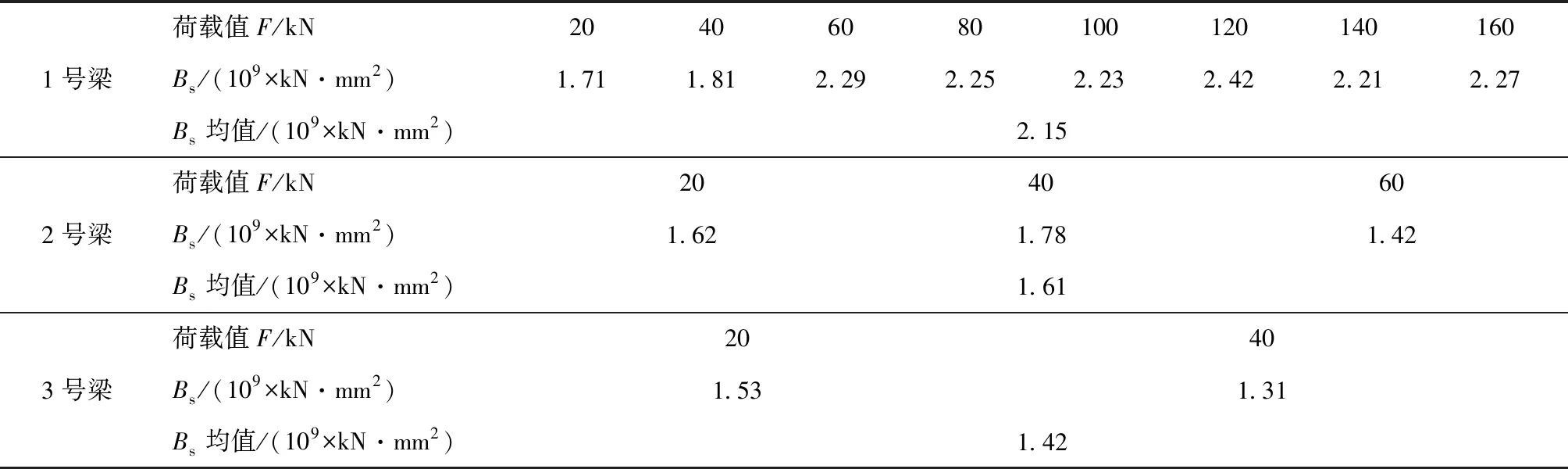
表4 1～3号梁的Bs值

由表4可见，混凝土的腐蚀与型钢的锈蚀会导致梁的抗弯刚度Bs下降，这对应于2.2节中规律(1)的原因分析。

进一步地，基于Bs值可根据梁在正常使用阶段的荷载情况和边界条件建立计算模型，用力学方法算出梁的最大挠度后与挠度极限值进行对比，实现适用性中变形条件的验算。例如，假设1号梁在正常使用阶段承受的是均布荷载，大小为q=6 kN/m，且可按简支梁考虑(已知其跨度l=2 m)，则根据结构力学可按式(3)计算其最大挠度：

(3)

计算结果为0.116 mm，相应的最大挠度/跨度比值为Δmax/l=1/17241<1/200(规范中的限值[4])，说明变形还没有超过限值。而如果是3号梁的话，计算结果为Δmax/l=1/11387，也没超过限值，但有了明显的放大。如果梁所受的均布荷载值增大，同时跨度也增大，则最大挠度有可能超过限值，影响到适用性。

4 结束语

本文针对型钢锈蚀与硫酸盐腐蚀耦合作用下的型钢混凝土梁，研究了三种耐久性不良情况下的适用性问题，进行了受弯变形性能的试验研究，并与完好状态下的梁进行了对比分析。研究结果表明，随着混凝土受硫酸盐腐蚀程度、型钢发生锈蚀程度的出现和加深，会引起以下规律性变化：(1)跨中挠度-荷载曲线的非线性段：逐步提前出现；(2)梁的延性：逐步增大；(3)极限挠度值：逐步下降；(4)梁的抗弯刚度Bs下降。同时分析了出现这些规律的主要原因。

进而给出了受硫酸盐腐蚀的锈蚀型钢混凝土梁的短期抗弯刚度Bs计算方法。基于此方法，可以确定出梁在耐久性不良的工况下的Bs值，进而可根据其在正常使用阶段的荷载情况和边界条件建立计算模型。再用力学方法算出梁的最大挠度，并与挠度限值进行对比，实现适用性中变形条件的验算，为受硫酸盐腐蚀的锈蚀型钢混凝土梁的适用性分析与设计提供了参考依据。