基于混合割线方程修正的L-BFGS算法

陈昱含

(重庆师范大学数学科学学院， 重庆 401331)

引 言

求解非线性无约束优化问题是最优化理论与算法研究方面最基本的问题，在许多高科技领域都有着重大的应用意义。本文中，考虑以下无约束优化问题：

(1)

其中，函数f:Rn→R是一个二次可微连续函数。BFGS方法是解决无约束优化问题的最有效的拟牛顿方法之一，具有良好的数值结果和理论收敛性。该方法通过更新对称矩阵Bk去逼近目标函数的Hesse矩阵，使其满足割线方程(拟牛顿条件)，即

Bk+1sk=yk

(2)

其中，sk=xk+1-xk,yk=gk+1-gk，Bk的更新公式如下

(3)

由于BFGS方法在每次迭代中都需要计算和存储更新的矩阵，将其应用于大规模优化问题时，效率可能会降低。为此，Liu[1]首先引入了有限记忆BFGS(L-BFGS)方法，这是对BFGS方法的改编。它可以看作是用额外的存储来加速收敛速度的共轭梯度法，也可以被视为存储受到限制的BFGS方法。它既克服了拟牛顿法计算量大的困难，同时又保持了良好的收敛性。

近年来，国内外许多学者积极投身到L-BFGS方法的研究中。Hou[2]利用Li[3]提出的割线方程对标准的L-BFGS方法进行修正，建立了在非凸假设和一定条件下的超线性收敛性。Biglari等人[4]为了改善目标函数的曲率信息，使用四阶张量模型导出了一个新的割线方程，提出了基于高阶张量模型的L-BFGS算法，并研究了该方法在一致凸问题上的全局和局部收敛性。Tarzanagh等人[5]针对文献[6-9]提出的几种割线方程，进行组合改进，提出了一种基于修正割线方程的正则化有限记忆BFGS型新方法，并在某些标准假设下，提供了新方法的全局收敛性。Dehghani等人[10]采用链式法则，在使用梯度值和函数值信息的同时，利用最近三个点的信息引入了不同的割线关系。并在非凸假设性条件下，建立了BFGS方法的全局收敛性。Razieh等人[11]基于Zhang[9]提出的割线方程提出了新的割线方程，该方程保证了对于一般函数，Hesse矩阵逆的近似Hk+1的正定性。Boggs等人[12]对储存大小m进行研究，提出了评估储存大小m好坏的有效度量，使得L-BFGS可以自适应选取m。

受以上文献的启发，关注到割线方程在非线性优化问题中起着核心作用。可以预测，通过修正割线方程，既可以保持拟牛顿法的大多数优良性质，又能更好的逼近目标函数的二阶曲率信息。为了利用L-BFGS方法获得更好的计算效果，本文基于Li[3]和Yuan[9]等人提出的两种割线方程，构造了一个新的割线方程，并将其应用到L-BFGS方法中求解大规模无约束优化问题。在一定假设条件下检验了该方法全局收敛性，并对其收敛速度进行了研究。

1 混合割线方程

一般地，在拟牛顿法的每次迭代中，都满足割线条件(2)。从该方程式很容易看出，对于给定的正定矩阵，如果满足以下条件：

(4)

通常称为曲率条件，则矩阵Bk+1是正定的。

为了更精确地近似Hesse矩阵，一些文献对割线方程进行了一些修改。一类方法是将函数值fk合并到梯度差yk中，另一类方法是把迭代点差sk合并到yk中。下面概述一些近年来提出的有效割线方程。

Zhang和Xu[8]推导出了一种具有向量参数的割线方程：

(5)

其中，ωk=3(gk+1+gk)Tsk-6(fk+1-fk),uk可以取sk，yk，或者gk。当uk取sk时，就退化到了Zhang等人[7]提出的割线方程，当uk取yk时，就退化到了Yuan[9]提出的割线方程。

(6)

uk=(1-θk)yk+θksk,θk∈[0,1]

(7)

数值试验结果表明，应用该割线方程改进的BFGS算法优于文献[6,9]中提出的改进的BFGS算法。这表明了所提出的混合割线方程的有效性。

此外，Li和Fukushima[3]等人提出了一种在非凸假设条件下依然保持全局收敛性的割线方程：

(8)

(9)

为了取得更好的数值结果，本文通过引入一个参数λ，对Li和Fukushima[3]以及Yuan[9]提出的两种割线方程进行凸组合，提出了一种新的混合割线方程如下：

(10)

其中，λ∈[0,1]，rk如式(9)所示。当λ=0，该方程就退化到了Li和Fukushima[3]提出的方程，当λ=1，该方程就退化到了Yuan[9]提出的方法。

2 修正的BFGS方法(ML-BFGS)

考虑以上提出的无约束优化问题(1)，标准的BFGS方法的迭代格式如下：

xk+1=xk+αkdk

(11)

dk=-Hkgk

(12)

其中，αk满足以下标准Wolfe条件：

(13)

(14)

其中，dk为搜索方向，gk为xk处的梯度，Hk为xk处Hesse矩阵逆的近似，则Hk可由以下形式的BFGS更新公式进行更新：

(15)

其中，

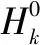
(16)

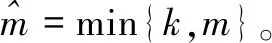
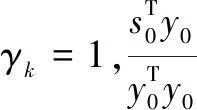
(17)

当取γk为1时，该方法就退化到了无记忆BFGS方法。本文采取Al-Baali[15]的取法，如下：

(18)

本文将新提出的混合割线方程应用到L-BFGS方法当中，提出了一个修正的有限记忆BFGS算法(ML-BFGS)方法，如下：

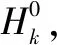
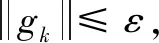
Step3利用Wolfe条件式(13)及式(14)计算αk(通常设第一次的步长为单位步长1)。

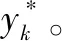
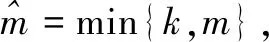
Step6令k=k+1，转Step2。

3 收敛性分析

在本节中，证明ML-BFGS方法在一致凸问题上是全局收敛的，并且其收敛速度是R-线性的。

假设A

1.目标函数f在Rn上下有界，在开集N上是二次连续可微的，

2.水平集L={x∈Rn|f(x)≤f(x0)}是凸的，其中L⊂N，x0为初始点，

3.存在正实数M1，M2，对于所有的z∈Rn和x∈L使得

(19)

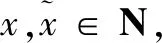
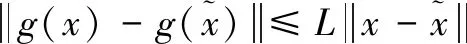
(20)

且αk满足Wolfe条件式(13)及式(14)，则

(21)

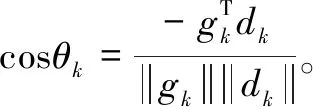
定理2设序列{xk}是由ML-BFGS算法生成的，若对任意的k有

(22)

则有

证明由引理1和Wolfe条件式(13)及式(14)可得

(23)

由式(22)可知，存在一个常数δ，使得对所有的k，有

cosθk≥δ>0

引理3[18]若a,b∈Rn，则有

tr(abT)=aTb=bTa

(24)

其中tr(abT)为abT的迹。

引理4[18]若u1,u2,u3,u4∈Rn，则有

(25)

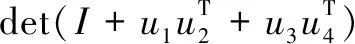
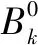
fk-f*≤rk(f1-f*)

(26)

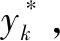
(27)

则由假设A、引理4～5可得式(26)，具体证明过程见文献[19]，又由x*处的泰勒展开公式和式(19)，可得

即

所以{xk}是R-线性收敛的。

4 数值实验结果

为了进行比较，本节中，将测试此算法ML-BFGS在一组测试问题上的数值性能，测试环境为华硕windows10操作系统Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz 1.80 GHz，4.00GB内存。

本文对CUTEr[19]中40个500-100000维的非线性无约束问题进行实验。其中每个问题都是规则的，即它的梯度和Hesse矩阵存在并且在各处都是连续的。对于每个测试问题，取ε=10-6，c1=10-2,c2=0.9，初始矩阵为γkI，γk的选取如式(18)所示。在用不同的m∈{3,20}处理了几个问题后，发现当m=5时，数值结果相对较好，所以本文中的实验取m=5。

下面对参数λ的选择进行讨论，当λ=0，割线方程就退化到了基于Li和Fukushima[3]提出的割线方程，当λ=1，割线方程就退化到了Yuan[9]提出的割线方程。因此本文提出以下三个策略：

LM1:m=5，λ=0，即基于Li和Fukushima[3]割线方程的L-BFGS方法；

LM2:m=5，λ=1，即基于Yuan[9]割线方程的L-BFGS方法；

LM3:m=5，λ=0.8，基于本文提出的混合割线方程的L-BFGS方法(ML-BFGS)

为了直观有效地比较标准L-BFGS、LM1、LM2、LM3四种方法的数值效果，本文绘制了基于CPU时间(以秒为单位)，函数计算次数，梯度计算时间和迭代次数的性能曲线，如图1～图4所示。

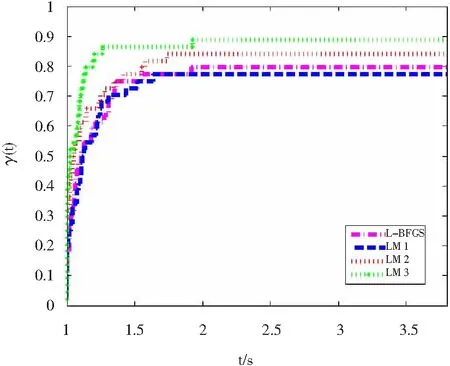
图1 基于cpu时间的性能概况

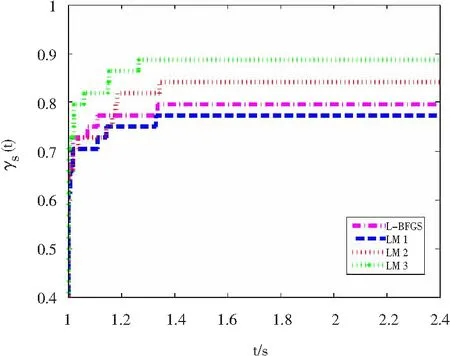
图2 基于函数计算次数的性能概况

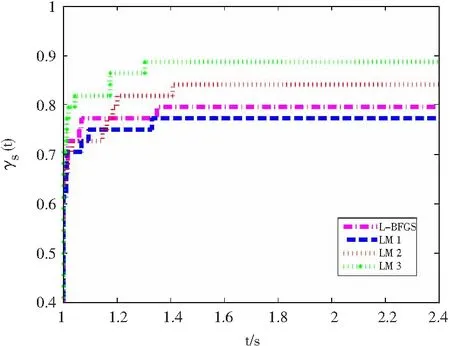
图3 基于梯度计算次数的性能概况

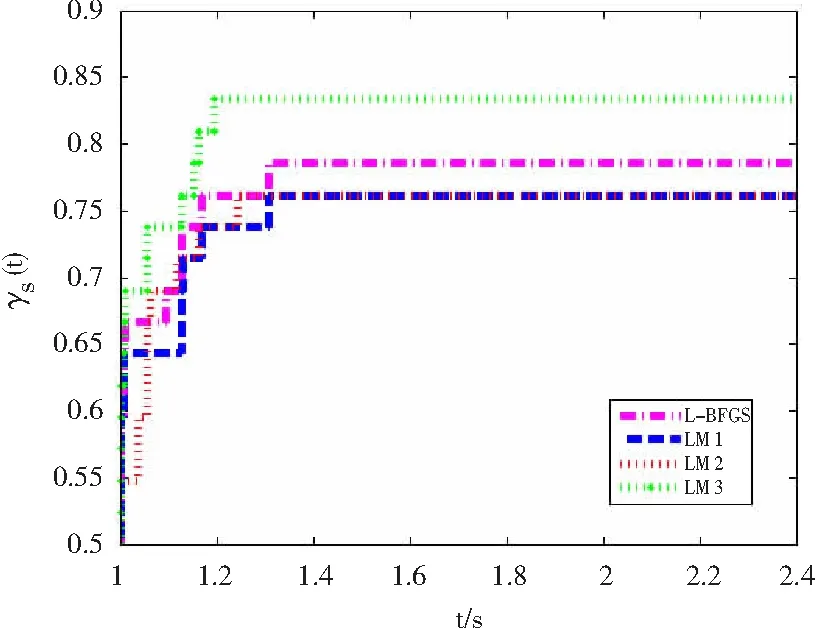
图4 基于迭代次数的性能概况

Dolan和Moré[20]的性能曲线图描绘了在最佳算法的给定因子(水平轴)内解决的问题(垂直轴)所占的比例，更有效的算法位于图的左上侧的“顶部”。因此，可以认为在整个图中处于“左上方”的算法比其他算法更有效。

从图1～图4可以看出，不论是CPU时间、函数计算次数，还是梯度计算时间和迭代次数，本文提出的ML-BFGS方法和其他三种方法都是极具竞争力的，可见本文提出的基于混合割线方程的L-BFGS算法在部分的问题上是优于其他三种算法的。

4 结束语

本文提出了一个新的混合割线方程，并将其应用到L-BFGS方法中，提出了ML-BFGS方法。在适当的假设下，保持了该方法在一致凸函数上的全局收敛性。数值结果表明，该方法在部分问题上优于其他三种方法。总的来说，本文提出的ML-BFGS算法通过修正割线方程提高了L-BFGS算法的计算效率，同时又保持了L-BFGS良好的理论收敛性。因此，该方法是有效的且与L-BFGS相比是极具竞争力的。