单轴冲击载荷下基于塑性细观力学的冻土本构模型研究

贾瑾宣， 朱志武， 张福来

(1.西南交通大学力学与工程学院， 成都 610031; 2.应用力学与结构安全四川省重点实验室， 成都 610031)

引 言

冻土是一种由固体矿物颗粒、粘塑性冰包裹体、液相水和气态包裹体四种基本成分所组成的复合体[1]。近年来，随着社会经济的发展，寒区工程建设成为中国基础建设的又一大热点。在此过程中，冻土在某些情况下将不可避免地受到冲击、爆炸等强动载荷的作用。同时，冻土由于其中冰的胶结作用而具有良好的承载能力，但冻土中冰的含量和胶结能力随外界温度的变化而变化。因此，对不同冻结温度下的冻土在冲击载荷下的动态力学行为及其本构模型研究便显得尤为重要。

目前，对于冻土冲击动态力学性能的研究还处于初始阶段。Lee等[2]通过对不同温度的冻土进行冲击压缩实验，发现冻土表现出了温度和压力依赖性、率敏感性、各向异性和体积压缩与膨胀。马芹永等[3]实验发现围压状态下冻土表现为粘塑性破坏，冻土力学行为有着明显的应变率效应和温度相关性。宁建国等[4]基于考虑应变率效应的Drucker-Prager屈服准则，采用各向同性硬化构建了冻土的动态弹塑性本构模型。朱志武等[5]通过实验发现冻土在冲击载荷下表现为分层破坏，并且建立了冻土的瞬时温升方程，得到了冻土有效弹性模量的表达式。刘志杰等[6]根据土基体在冲击加载下层层破坏的特点，在土基体的弹性模量中引入应变率项，建立了冻土的细观本构模型。谢奇峻等[7]把冻土考虑为土颗粒和冰组成的两相复合材料，采用脱粘损伤理论建立了描述应变率效应的细观本构模型。伏甜甜等[8]以塑性本构框架为基础，考虑到冻土的应变率效应以及微裂纹和微孔洞的损伤演化规律，建立了描述冻土动态力学行为的本构模型。综上所述，目前冲击载荷下冻土动态本构模型的建立主要集中于损伤力学和细观力学等方面，而从细观力学角度对冻土率相关塑性变形的研究相对很少。

本文利用分离式霍普金森压杆对不同冻结温度下冻土进行了不同应变率的单轴冲击压缩实验，获取了相应的动态应力-应变曲线。进而，分析了冻土的动态变形和强度特征，探究了冻土的温度和应变率效应。基于实验结果，采用细观力学的平均化方法推导了与冻结温度相关的冻土等效弹性常数的表达式。同时，采用基体各向同性化的切线模量法建立了冻土的动态塑性细观力学模型。进而，引入与冻结温度和加载应变率相关的连续损伤演化模型，构建了冻土的冲击动态本构模型。相应的计算结果表明该模型能够很好地描述冻土的动态力学行为。

1 实验研究与结果分析

1.1 实验研究方法

本文实验研究采用变截面分离式霍普金森压杆(SHPB)。同时，本文实验研究采用了脉冲整形技术，将一个放置在入射杆冲击平面上的黄铜片用作脉冲整形器。对于有效的SHPB实验，波形整形器有助于实现应力平衡和恒应变率加载[9]。

实验采用的冻土试样来源于成都黏土。试样尺寸为Φ30 mm×18 mm，密度为2.07 g/cm3，含水率为30%。

制作试样时，首先将黏土碾散，置于温度为105 ℃的烘干箱中烘干12 h。接着，将土颗粒分别用筛孔直径为2 mm、0.85 mm、0.425 mm和0.18 mm的筛子依次过筛，得到土样的颗粒级配。然后，取颗粒尺寸小于2 mm的土颗粒加蒸馏水至所需初始含水量并搅拌均匀，放入密闭容器中密封保持6 h。随后，整体压实装入到试样筒中的湿土。最后，将土样放入恒温箱中冷冻24 h。

本文对三种不同冻结温度下(-10 ℃、-15 ℃和-20 ℃)冻土试样进行加载气压为0.1 MPa～0.6 MPa的单轴冲击压缩实验，每种加载工况下实验重复2～3次。由“二波法”处理得到试件在高应变率下的动态应力-应变曲线[10]。

1.2 实验结果与分析

实验得到的不同不同温度各加载应变率下冻土的动态平均应力-应变曲线如图1(a)～1(c)所示。

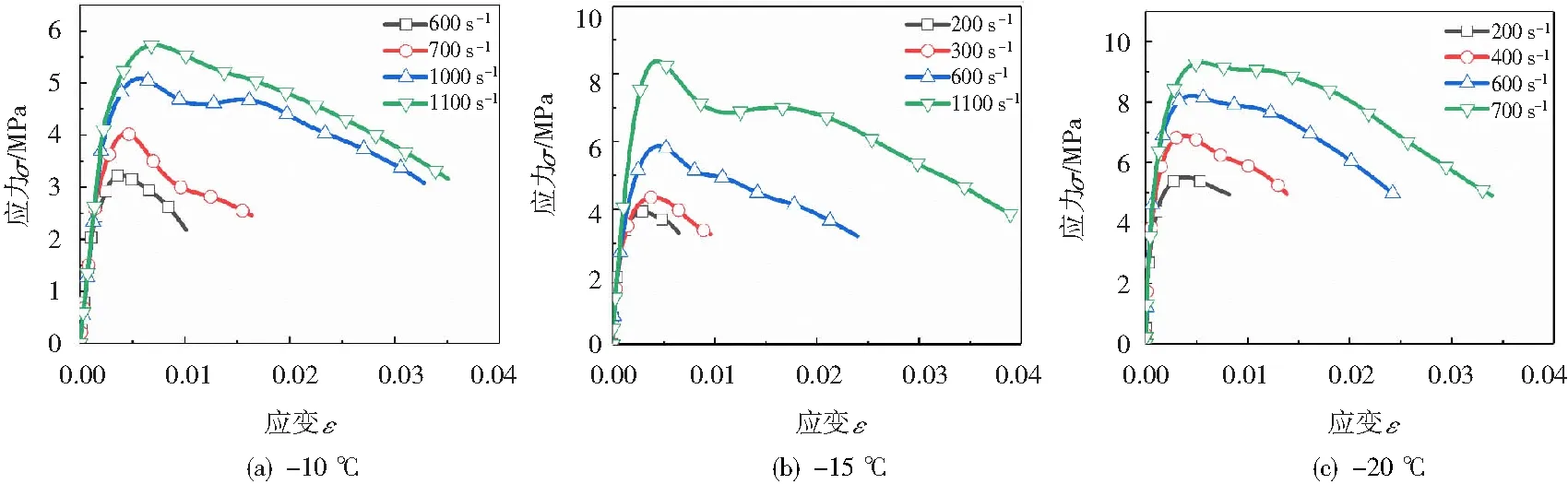
图1 不同温度下各加载应变率下冻土的动态应力-应变曲线

本文将冻土的动态应力-应变曲线上升段曲线斜率发生明显变化的点定义为初始屈服点，并且将该点处的割线模量定义为材料的弹性模量。图1可见，在冻土变形的初始阶段应力-应变曲线基本保持重叠不变。可以认为，相同冻结温度下冻土的弹性模量与应变率无关，为常数值。这是因为，从复合材料细观力学角度看，冻土中的土颗粒和孔隙冰在冲击载荷下弹性模量便没有明显的应变率相关性，孔隙水主要作用于冻土塑性变形阶段[11-13]。

不同冻结温度下，冻土的初始屈服强度与应变率之间的关系，以及峰值强度与应变率之间的关系分别如图2和图3所示。

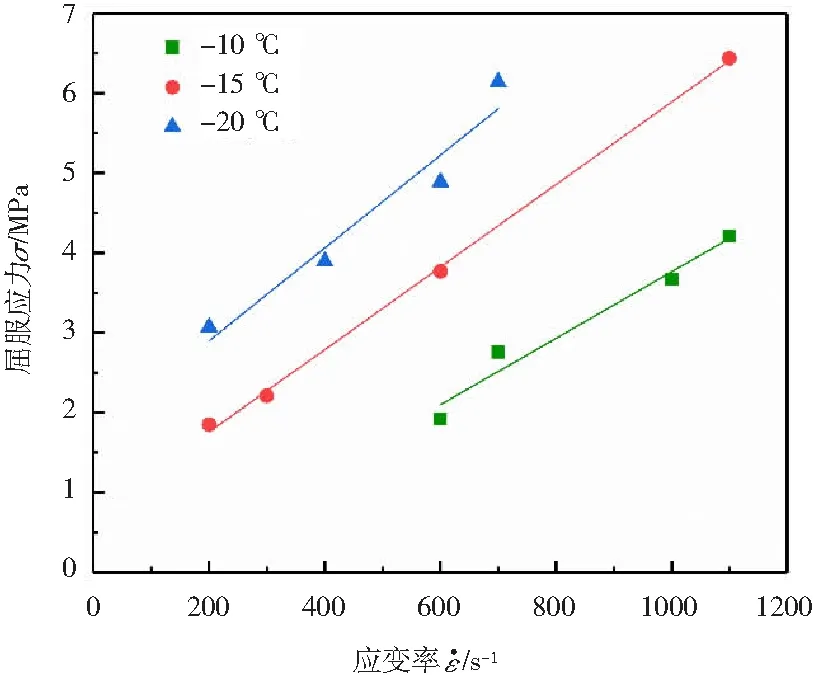
图2 不同冻结温度下屈服强度与应变率之间的关系

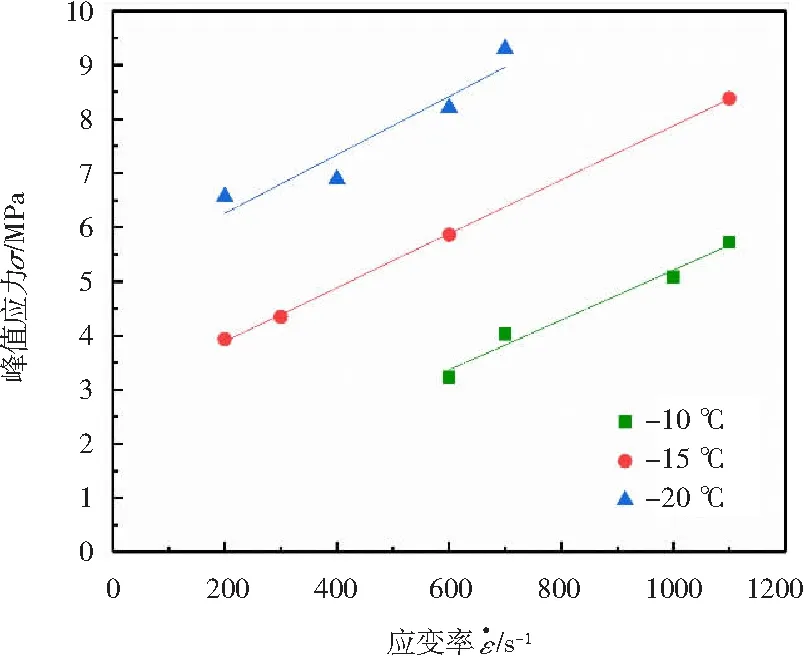
图3 不同冻结温度下峰值强度与应变率之间的关系

由图2和图3可见，冻土的强度随着应变率的升高而增大，冻土的力学性能有着明显的应变率强化效应。这是因为冻土中的土颗粒和孔隙冰都具有明显的应变率强化效应[11-12]。

加载应变率约为600 s-1时，不同冻结温度下冻土的动态应力-应变曲线如图4所示。

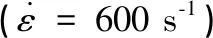
由图4可见，在变形的初始阶段，冻土的弹性模量随着冻结温度的降低而增大。并且，相同应变率下冻土的强度随着冻结温度的下降而升高。冻土的力学性能也有着明显的温度效应。这是因为随着冻结温度的降低，冻土中未冻水含量降低，土壤基质吸力变大，含冰量升高，冰的弹性模量和强度升高，从而使得冻土的承载能力更强[14]。

2 本构模型

2.1 冻土的等效弹性常数

冻土作为一种四相复合体，其中每一种组成成分的比例、性质和相互作用都影响着材料的力学性能。特别地，其中孔隙冰的性质及其与土颗粒的胶结作用明显地影响着冻土的力学性质。忽略孔隙水和气体对冻土力学性质的影响，把冻土考虑为土颗粒和冰胶结物构成的复合材料。

假设冻土中的土颗粒和冰都为均匀各向同性材料，且它们之间完全胶结。根据细观力学平均化方法，可假定土基体和冰夹杂中的平均应力等于外加应力[15]。当施加常宏观应力σ0在代表性体积单元(RVE)边界上时，则有：

(1)

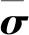
由实验结果的分析易知，在冲击载荷下土颗粒和冰在变形的初始阶段均能表现出较好的线弹性特征，且可忽略应变率效应，把弹性模量的大小近似为常数。所以，冲击载荷下土颗粒和冰的弹性应力-应变关系用广义胡克定律表示为：

εs=Cs：σs

(2)

εi=Ci：σi

(3)

式中，εs为土基体的平均应变，εi为冰夹杂的平均应变；Cs为土颗粒的柔度张量，Ci为冰的柔度张量。

(4)

式中，fs和fi分别为土基体和冰夹杂的体积分数，且满足关系式：

fs+fi=1

(5)

(6)

从而，冻土的等效弹性模量E和等效泊松比ν可以表示为：

(7)

(8)

式中，Es和Ei分别为土颗粒和冰的弹性模量；νs和νi分别为土颗粒和冰的泊松比。

由于表面自由能的存在，土颗粒和冰在负温情形下会吸附一定量的未冻水。徐雪祖[16]通过研究认为不同土质的冻土中未冻水含量与冻结温度之间存在如下关系：

Wu=AT-B

(9)

式中，Wu为未冻水含量；T为冻土冻结温度的绝对值；A、B分别为与土质有关的常数。

已知冻土的初始含水量为W，在本文中W=30%，则不同冻结温度下冻土中含冰量Wi为：

Wi=W-Wu

(10)

因此，冻土中冰的体积分数为：

(11)

式中，Ms为冻土中土颗粒的质量，本文中其值为20.36 g；ρi为冰的密度，其值为0.9 g/cm3；V为冻土试样的体积，其值为12.72 cm3。

将式(9)～式(11)代入到式(7)和式(8)中并且考虑到不同温度下各组分弹性常数的变化，便可得到与冻结温度变化有关的冻土等效弹性常数的表达式。

2.2 塑性细观力学模型

细观力学平均化方法要求基体和夹杂都必须是线弹性的，只有这样材料等效弹性常数的表达式才能成立。但是，大量的实验研究表明，在冲击载荷下土颗粒会发生明显的破碎和重排列，土体发生不可恢复的塑性变形[17]。所以，冻土冲击动态本构模型的建立理应考虑内部组分塑性变形的影响。

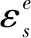
(12)

则土颗粒的弹性应力-应变关系可以表示为：

(13)

同时考虑土颗粒为各向同性硬化，则准静态下土颗粒的加载函数可以表示为：

(14)

(15)

式中，D、P为材料常数。

从而，与加载应变率有关的土颗粒的动态屈服条件可以表示为：

(16)

(17)

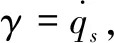
利用Kuhn-Tucker加载/卸载条件来引入塑性流动的不可逆性，即：

γ≥0，f≤0，γ·f=0

(18)

式中，γ由一致性条件确定，即：

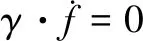
(19)

综上所述，冲击载荷下土颗粒的动态塑性本构模型可以由式(13)，式(15)～式(19)构成。进而，采用基体各向同性化的切线模量法建立冻土的动态塑性细观力学模型[19]。当土颗粒发生塑性变形时，在一个无限小的加载步内，依据一致性条件，可得：

(20)

求解上式，可得在这一加载步内塑性乘子的大小为：

(21)

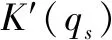
从而，由式(13)和式(21)可得在这一无限小的加载步内土颗粒的应力-应变关系为：

当γ=0时，dσs=Esdεs

(22)

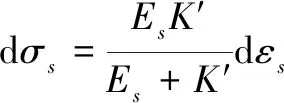
(23)

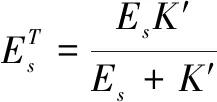
此外，冲击载荷下冰表现为脆性断裂，在强度达到峰值应力之前，其本构模型可用线弹性模型来表征[20]。所以，在某一加载步内冰的应力-应变关系为：

dσi=Eidεi

(24)

因此，基于式(7)，增量形式的冻土动态塑性细观力学本构模型为：

dσ=Edε

(25)

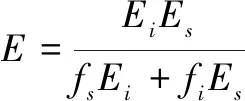
(26)

(27)

特别地，由式(4)和式(12)可得冲击载荷下冻土的塑性应变为：

(28)

同理，如果考虑到冻土内部组分与温度变化有关的本构参数的变化，则上述本构模型将能同时表征冻土力学行为的温度效应。

2.3 连续损伤演化律

冲击载荷下冻土在变形过程中随着绝热温升所致的热软化和材料内部微裂纹、微孔洞损伤的演化积累，冻土的变形由应变硬化转化为应变软化，材料的承载能力逐渐丧失。

根据Lemaitre应变等效性假设，受损冻土的本构关系可通过将名义应力替换为有效应力用无损时的本构关系表示[21]。其中，有效应力可以表示为：

(29)

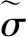
由实验分析可知，冻土在变形的初始阶段可以表现出较好的线弹性特征。因此忽略冻土的弹性损伤，考虑冻土的损伤演化与塑性变形有关。基于塑性应变率的Arrhenius方程，将连续损伤D的演化视为一个类似于热激活的过程，则可以得到率相关的连续损伤演化律为[22]:

(30)

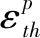
设塑性应变阈值为零，则冻土的损伤演化方程可以简化为：

(31)

进一步，考虑到不同冻结温度条件下岩土材料内部水分迁移、分凝冰体形成及材料结构的变化，而材料细观损伤的演化与温度变化密切相关[23]。因此，通过引入一温度项来表征冻结温度变化对于冻土连续损伤演化规律的影响，即：

(32)

式中，α和β为材料参数；T*=(T-Tr)/(Tm-Tr)，T为冻土的冻结温度，Tr为参考温度，本文取值为253.15 K，Tm为冻土的熔点，取值为273.15 K。

式(32)显式地刻画了冻土连续损伤的演化同时依赖于塑性应变、塑性应变率和冻结温度，该式可以用来表征各种广义损伤的演化。

3 本构模型的验证

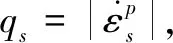
(33)

式中，M和N为硬化参数，通过土颗粒的冲击动态压缩实验获得。不同冻结温度下具体的材料参数见表1。

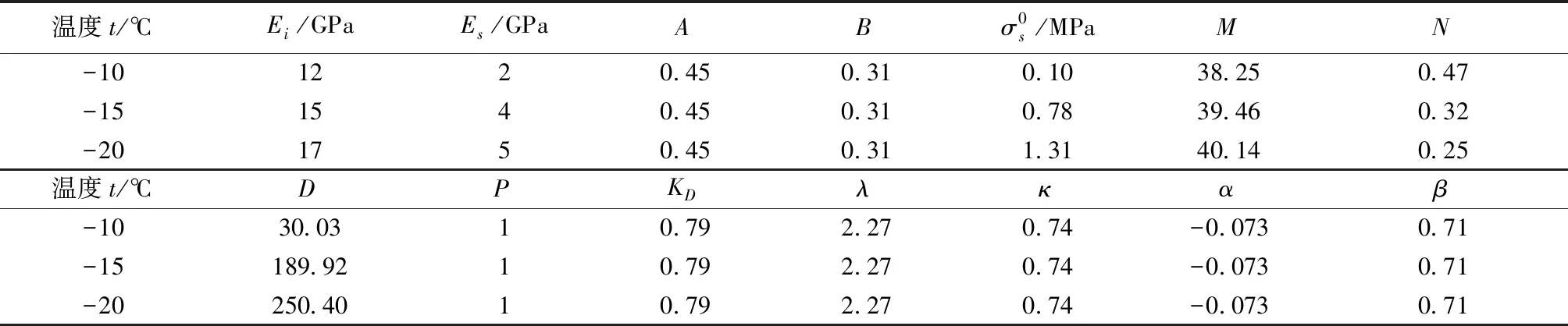
表1 本构模型的材料参数

对本文建立的本构模型进行数值求解。不同加载条件下实验应力-应变曲线与理论计算应力-应变曲线的对比如图5所示。

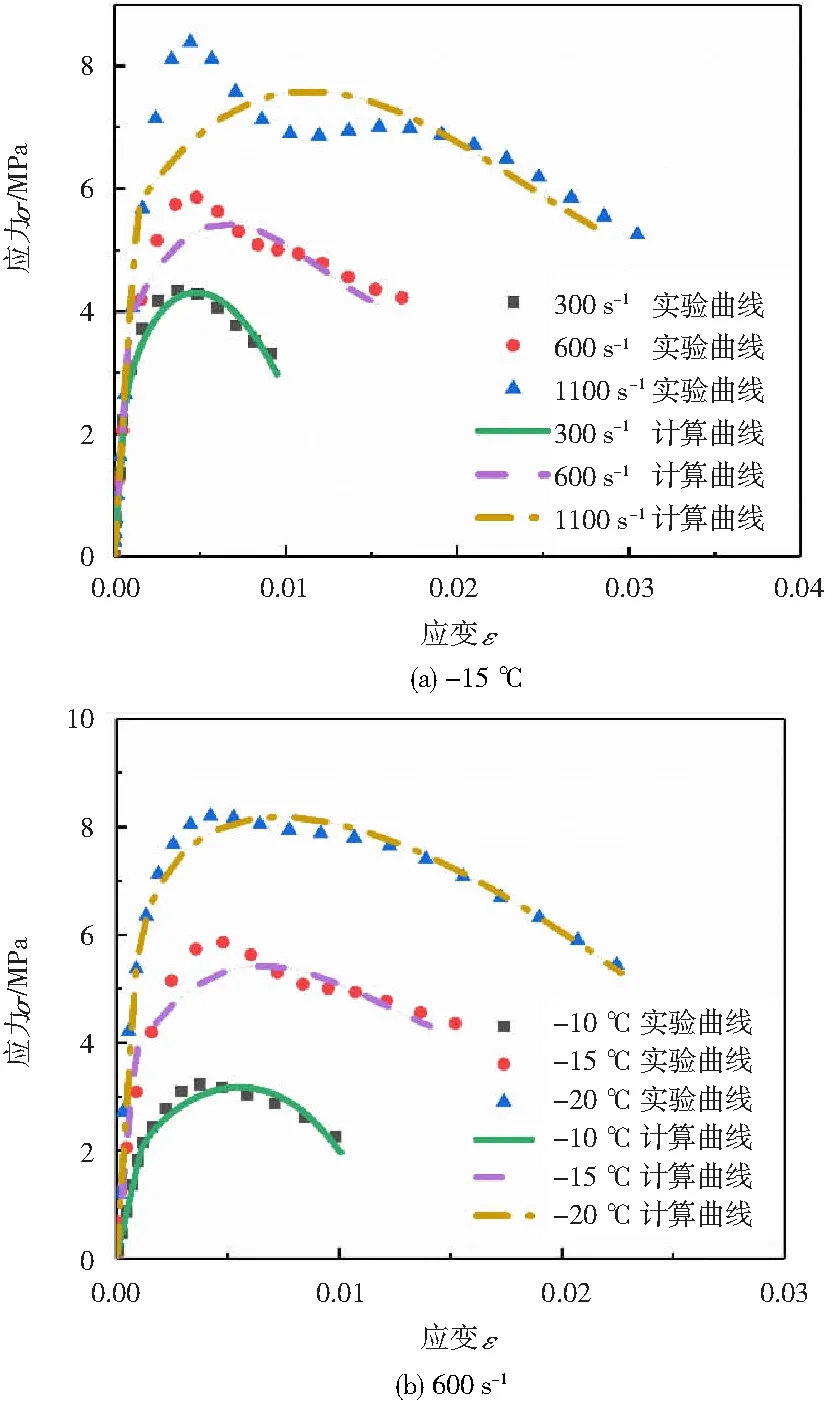
图5 冻土在不同加载条件下实验曲线与理论曲线的比较

由图5可见，理论计算曲线与实验实测曲线的变化趋势是一致的。本构模型能够较好地表征冻土的动态变形及强度特征。同时，本构模型能够较好地反映冻土动态力学性能的应变率效应，也能很好地反映冻土动态力学性能的温度效应。因此，本文所构建的冻土冲击动态本构模型具有较好的理论实践意义。

4 结 论

(1)通过采用SHPB设备对不同冻结温度的冻土试样进行不同应变率的冲击加载实验，获得了冻土的动态应力-应变曲线。实验结果表明，相同冻结温度冻土的动态力学性能有着明显的应变率效应：冻土的强度包括初始屈服强度和峰值强度随着应变率的升高而增大；冻土的弹性模量没有明显的应变率相关性。

(2)冲击载荷下冻土的动态力学性能表现出明显的温度效应：随着冻结温度的降低，冻土的弹性模量变大，相同应变率下冻土的强度包括初始屈服强度和峰值强度升高。

(3)根据实验结果，本文基于细观力学平均化方法，推导出了不同冻结温度下冻土等效弹性常数的表达式。进而，采用基体各向同性化的切线模量法，建立了冻土的动态塑性细观力学模型。最后，引入与冻结温度和加载应变率相关的连续损伤演化模型，构建了冻土的冲击动态本构模型。相应的模拟结果表明，该模型能够很好地描述冻土的动态力学行为。该本构模型的建立在深化冻土冲击动态本构模型的研究上提供了一种新的分析思路。