时变外磁场下海森堡自旋链的热纠缠

黄利元

(厦门大学嘉庚学院信息科学与技术学院， 漳州 363105)

1 引 言

量子纠缠作为量子通信和量子信息处理的重要物理资源[1-4]，在量子信息学的各方面都起着举足轻重的作用.近年来，一种自然界的纠缠现象――热纠缠，逐渐得到人们的重视.这种存在于固态系统中自旋粒子间的纠缠为量子信息和固态物理系统提供了一座桥梁.海森堡模型作为最简单而又实际的固态物理系统，被认为是实现量子通信和量子计算最有前景的物理体系之一[5].海森堡模型在热平衡状态下的量子纠缠――热纠缠已经被广泛地应用于量子计算[6]、量子密码[7]等各个领域.

目前，有关海森堡模型在均匀磁场和非均匀磁场情况下纠缠性质的研究取得了广泛进展[8-16]，但对在时变磁场下系统纠缠性质的研究[17-19]还不多见.而时变磁场对纠缠度的作用机理更加接近固态系统中量子信息的实现.本研究主要讨论时变外磁场对海森堡XXZ链的热纠缠和时间纠缠的作用.

2 模 型

考虑两个角频率不同的余弦时变磁场分别加在Heisenberg XXZ链的两个量子比特上.此时系统的哈密顿量可以写为：

(1)

(2)

其本征态及相应的本征值为：

|φ1〉=|00〉，

|φ2〉=|11〉,

|φ3,4〉=sin±|01〉+cos±|10〉

(3)

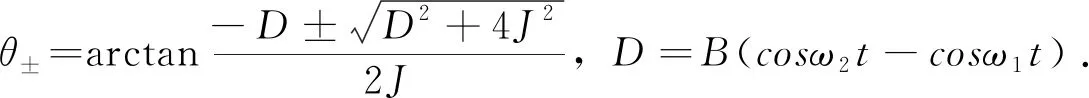
E1=JΔ+B(cosω1t+cosω2t),

E2=JΔ-B(cosω1t+cosω2t),

(4)

哈密顿量为H的热态也可以写成如下形式：

(5)

式中β=1/(kT)，k为玻尔兹曼常数，简单起见记为1，T为热力学温度,H为系统哈密顿量，Z=tr[exp(-βH)]为配分函数.因为ρ(T)表示的是热态，所以该态内的纠缠称为热纠缠[20]. 在标准基{ |00〉,|01〉,|10〉,|11〉}下,

(6)

式中

u=exp[-β(J△+Bcosω1t+Bcosω2t)],

v=exp[-β(J△-Bcosω1t-Bcosω2t)],

Z=2exp(-βJ△)cosh[βB(cosω1t+Bcosω2t)]+

(7)

3 热纠缠

对于两量子比特的纠缠度，ρ12可以是纯态也可以是混合态.Concurrence[21]纠缠度定义为：

C12=max{λ1-λ2-λ3-λ4, 0},

(8)

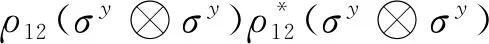
根据上述定义，密度矩阵的纠缠度C为：

(9)

如图1所示，纠缠度C随ω2周期性变化，周期为4，且在一个周期内，图形关于ω2=2对称，这是由cos函数的特点决定的.从图1的任意一幅子图可以看出，当ω1一定时，随着ω2的增大，纠缠度C在经历一个较小的波峰(次极大值)后迅速降到主极小值0 (即系统失去纠缠).然后又迅速达到一个新的更高峰，此时C取主极大值，随后C缓慢下降，在ω2=2处形成一个波谷，取次极小值.因此，当ω1一定时，可以通过选择合适的ω2使系统维持在较大的纠缠度上.

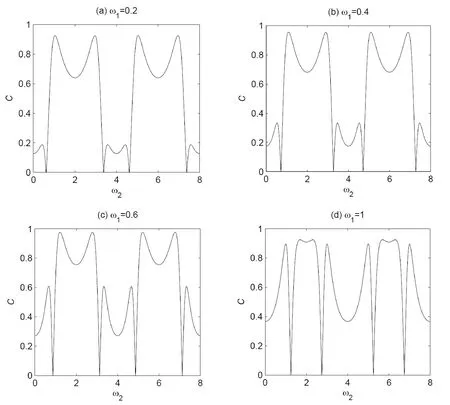
图1 当角频率ω1不同时，纠缠度C随角频率ω2的变化.自旋耦合常数J=1，温度T=1，各向异性参数△=1，均匀磁场B=3，时间t=π/2.(a) ω1=0.2； (b) ω1=0.4； (c) ω1=0.6； (d) ω1=1.Fig.1 The thermal entanglement measured by the concurrence C as a function of the angular frequency ω2 for different angular frequencies ω1.The coupling constant J=1, the temperature T=1, the anisotropic parameter △=1， the uniform magnetic field B=3 and the time t=π/2.(a) ω1=0.2； (b) ω1=0.4； (c) ω1=0.6； (d) ω1=1.

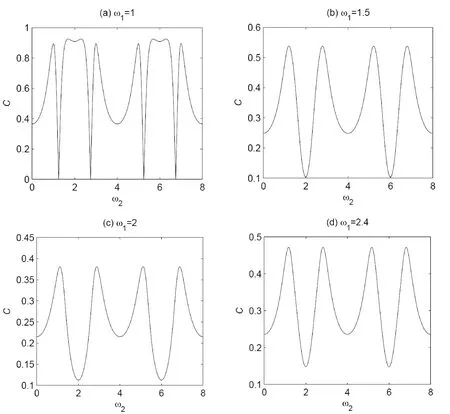
图2 当角频率ω1不同时，纠缠度C随角频率ω2的变化.自旋耦合常数J=1，温度T=1，各向异性参数△=1，均匀磁场B=3，时间t=π/2.(a) ω1=1； (b) ω1=1.5； (c) ω1=2； (d) ω1=2.4.Fig.2 The thermal entanglement measured by the concurrence C as a function of the angular frequency ω2 for different angular frequencies ω1.The coupling constant J=1, the temperature T=1, the anisotropic parameter △=1， the uniform magnetic field B=3 and the time t=π/2.(a) ω1=1； (b) ω1=1.5； (c) ω1=2； (d) ω1=2.4.

在一定范围内，随着ω1值的增大，小波峰上的C的次极大值增大，主波峰上的主极大值先增大后略有减小，但两主极大值之间的值保持增加趋势，向主极大值靠近，即使C取较大值的ω2的范围变大了.但需注意的是，纠缠度C除了波谷的次极小值对应的ω2值(=2)没变，其余取主极大值、次极大值及最小值0的ω2值都变了，而且都向对称轴ω2=2靠近.

纵观图1的4幅子图，发现，选取某一特定时刻，当ω1一定时，纠缠度都有主极大值、次极大值、主极小值、次极小值，对应着图中的主波峰、次波峰、主波谷、次波谷.即在某一时刻，当ω1一定时，可选择合适的ω2使系统C取最大值，以满足需要.对比图1的4幅子图，发现，在一定范围内，随着ω1值的增大，主极大值呈先增大后减小的趋势.

图2中的ω1的取值跨度比图1大些.发现，在一定范围内，随着ω1值的增大，纠缠度C的主极大值变小.所以当t一定时，ω1值不宜太大.还发现，随着ω1值的进一步增大，原来取次极小值的位置变成了主极小值(ω2=2处)，而且主极小值逐渐升高，但主极大值则在C=0.4附近振荡.

对比图2和图3，当t不同时(即选取的时刻不同)，图形的周期不同，出现不同规律的ω1值不同.图2和图3除了选取的时刻不同，其它参数都一样.发现t=π/4相比t=π/2时，ω2可以在较大的范围内使系统保持在相对稳定且较大的纠缠度C上.

图4给出了当ω1和ω2取不同的确定值且相互之间呈一定的倍数关系时，C随t变化的曲线图.发现，当ω1=ω2时，纠缠度C虽然呈周期性变化，但始终能保持较大的值，在0.8174到0.8956之间.这对系统需要较大纠缠是有意义的.当ω1和ω2呈现其它的倍数关系时，根据C的变化情况，如纠缠突然死亡到迅速恢复，这种情况可以用作快速反应开关.

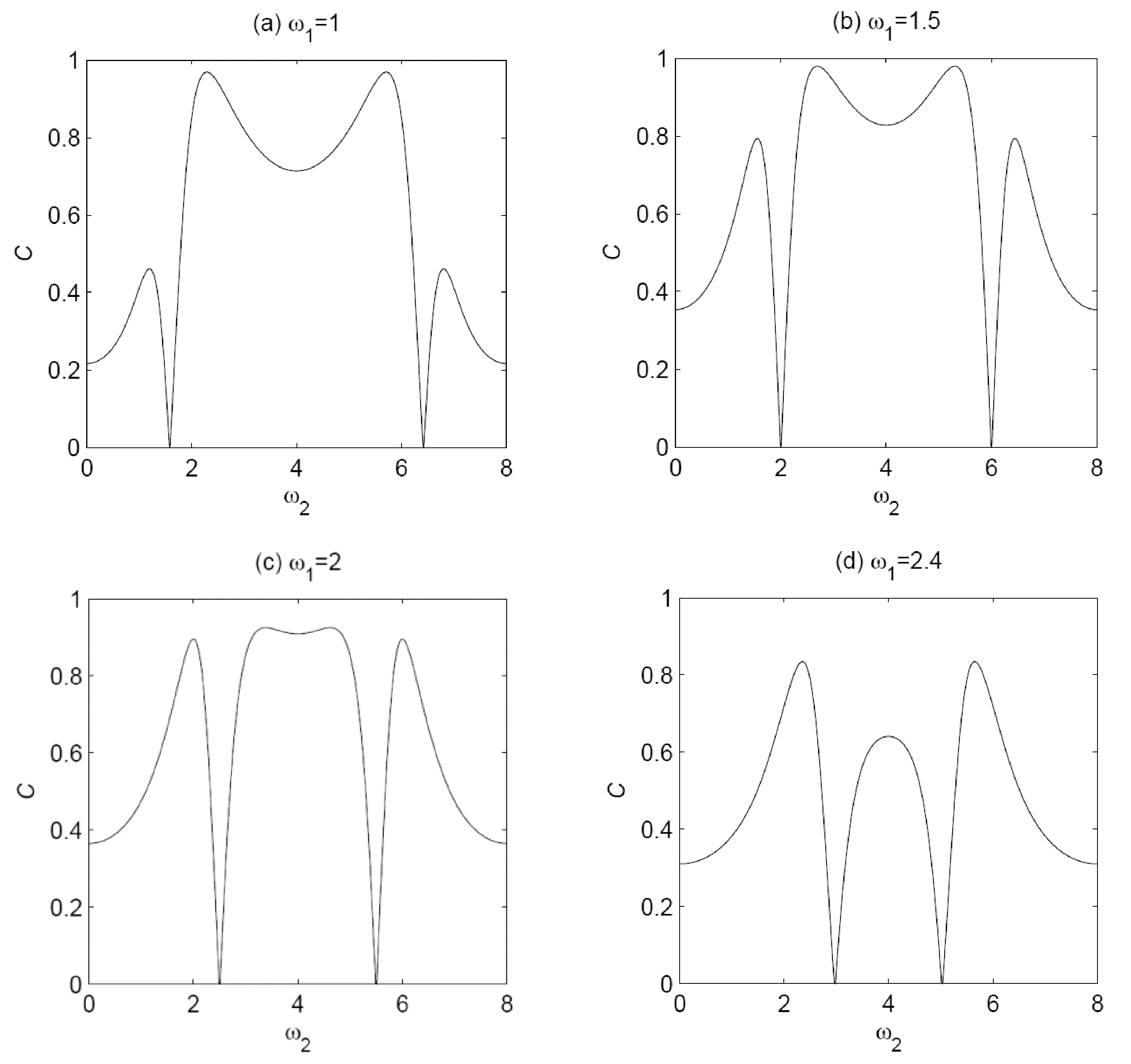
图3 当角频率ω1不同时，纠缠度C随角频率ω2的变化.自旋耦合常数J=1，温度T=1，各向异性参数△=1，均匀磁场B=3，时间t=π/4.(a) ω1=1； (b) ω1=1.5； (c) ω1=2； (d) ω1=2.4.Fig.3 The thermal entanglement measured by the concurrence C as a function of the angular frequency ω2 for different angular frequencies ω1.The coupling constant J=1, the temperature T=1, the anisotropic parameter △=1, the uniform magnetic field B=3 and the time t=π/4.(a) ω1=1； (b) ω1=1.5； (c) ω1=2； (d) ω1=2.4.

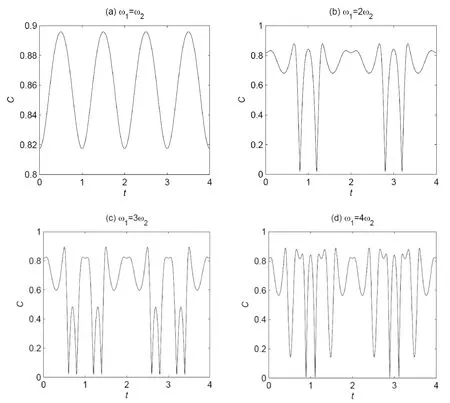
图4 当ω1和ω2为不同的倍数关系时，纠缠度C随时间t的变化.自旋耦合常数J=1，温度T=1，各向异性参数△=1，均匀磁场B=1，ω2=π， (a) ω1=ω2； (b) ω1=2ω2； (c) ω1=3ω2； (d) ω1=4ω2. Fig.4 The thermal entanglement measured by the concurrence C as a function of the time t for different multiple relationship of angular frequencies ω1 and ω2.The coupling constant J=1, the temperature T=1, the anisotropic parameter △=1, the uniform magnetic field B=1 and ω2=π， (a) ω1=ω2； (b) ω1=2ω2； (c) ω1=3ω2； (d) ω1=4ω2.

4 结 论

对于两量子比特的海森堡XXZ自旋链，本研究通过将两个角频率为ω1和ω2的余弦时变外磁场分别加在这两个量子比特上，得到其纠缠度与ω1和ω2的解析表达式，以及纠缠度随时间的变化情况.研究发现，当选取的时刻一定时，纠缠度会随着ω1和ω2值的变化而变化.特别地，当ω1和ω2的取值组合恰当时，系统可以维持在较大的纠缠度上.因此，在某一时刻，当ω1一定时，总可以通过选择合适的ω2使系统的纠缠度较大.结果还表明，当ω1=ω2时，系统的纠缠度虽然会随时间发生周期性变化，但始终能维持在较高的值.而当ω1和ω2为其它的倍数关系时，根据纠缠度的变化情况可以用作快速反应开关.本研究的计算结果对固态系统中通过构建和选择参数调整系统的纠缠度具有一定的作用和意义.