考虑轨迹相似度的综合客运枢纽出租车合乘方法研究

吴玥琳，袁振洲*，陈秋芳，肖清榆，王文成，魏 来

(1.北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京100044；2.越南河内交通大学工程学院，河内100803，越南)

0 引言

乘客等候出租车时间过长已成为综合客运枢纽运营的一大问题.出租车时常仅搭载1～2名乘客造成运力资源浪费，无法疏解等待乘客.出租车合乘能有效提高出租车使用效率，节约运力资源，减少旅客排队等待出租车的时间.因此，研究枢纽合乘问题具有很强的实践价值.

学者对合乘问题已有相关成果：Martinez等提出基于折扣的合乘模式，利用合乘费用优惠吸引更多的人参与合乘[1]；程杰等考虑乘客对性别偏好建立动态合乘模型，利用遗传算法求解[2]；丁冉以总时间和总费用最小为目标，收益、容量等为约束建立动态合乘匹配模型[3].优化算法方面：Coslovich针对动态合乘问题提出路径干扰的实时两阶段插入法[4]，肖强等利用隶属度函数对乘客和出租车的合乘进行动态模糊识别[5]，邵增珍等建立了基于松弛路程、线路拟合度、车辆剩余容量等匹配度指标，形成算法解决静态合乘匹配任务分派问题[6].

现有研究集中于路网合乘，对枢纽合乘问题研究较少且在乘客对行驶轨迹形态要求方面未充分考虑.事实上，路网合乘问题是根据出租车原始行程作为基准匹配乘客，因乘客需求不集中，可行方案较少.而枢纽合乘问题无原始路线基准且乘客需求量大，使得乘客间可行匹配组合远多于路网合乘，优化复杂度较大.另外，路线作为重要的匹配条件，现有研究大多注重需求起终点的相近和路线长短的约束，较少研究行驶轨迹的形态相似性以满足乘客的心理预期.

据此，本文将车辆数最小和总行驶距离最短为目标函数，考虑乘客对行驶轨迹预期添加轨迹相似性度量约束，构建考虑轨迹相似度的出租车合乘模型.提出两阶段算法，第1阶段基于出发时间和方向角对需求进行聚类，第2阶段设计蚁群算法求解模型得到合乘方案.实验结果证明：所提模型与算法能够同时优化车辆数和总里程，减少乘客绕行比例和等待时间，加快枢纽旅客疏散；在轨迹形态方面为合乘匹配研究提出新的角度和思路，为综合客运枢纽的出租车合乘组织提供一定的实践依据.

1 问题建模

1.1 模型假设

考虑综合客运枢纽乘坐出租车的实际情况，结合本文研究需求，假定：

(1)参与合乘乘客的所有需求信息可提前在线获取.

(2)出租车比乘客提前到达候车区，乘客均到达后即驶离枢纽.

(3)车辆行驶匀速且所有出租车速度相同.

(4)路网道路通畅，不考虑行驶过程中拥堵等随机扰动影响.

1.2 模型建立

引入有向网络G={N,A}，N是点集合，A是边集合，i,j,u是每个乘客的需求终点索引，i,j,u∈N，0表示枢纽点.a(i,j)表示点i行驶至点j，a(i,j)∈A，利用轨迹点作为行驶轨迹的表现形式，i至j途经轨迹点不反映在网络G当中，而是作为a(i,j)的属性数据.不考虑出租车返回枢纽的情况，将集合N中的需求终点按照与枢纽的距离升序排列.dij是i至j最短距离，rij是i至j的最短轨迹，途经点集是需求i的最早出发时间，τ是乘客最长等待时间；是i的最晚到达时间，ti是到达i的实际时间，s是每个需求点的服务时间；V是行驶速度；K是所需出租车集合，k是出租车索引，k∈K，c是车辆容量；θsim是轨迹相似性度量指标(见1.3节)，λ为相似性度量阈值；xijk为0-1决策变量，车辆k通过a(i,j)，xijk=1，否则，xijk=0，xiuk,xujk的定义与取值同xijk.

为应对枢纽高峰时期出租车运力不足及避免周边交通压力，以所需出租车数量最小为目标；同时，为兼顾运输效率，选取总行驶里程最小为目标，构建双目标模型为

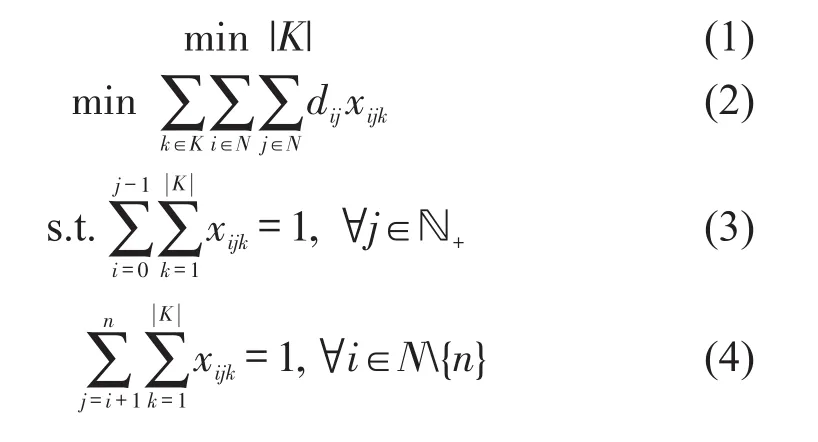
目标函数：式(1)最小化出租车所需数量，式(2)最小化所有车辆的行驶总里程.约束条件：式(3)和式(4)确保每个乘客能且只能乘坐一辆出租车；式(5)和式(6)表示所需出租车均从枢纽出发，服从先近后远的规则；式(7)确保流量平衡；式(8)为容量约束，即每辆出租车搭载乘客不超过c；式(9)和式(10)是时间窗约束，为减少乘客的排队时间，加快旅客疏散，要求每位乘客在前乘坐出租车离开，即同乘一辆出租车乘客的最晚出发时间与最早出发时间的差值不超过τ；式(10)要求乘客在之前抵达终点；式(11)是轨迹相似度约束，表示合乘前后的轨迹相似性度量指标需大于阈值λ，表示合乘后k车到达j点之间的所有路径轨迹，表示合乘前枢纽点0到j点的路径；式(12)是决策变量0-1整数约束.

1.3 轨迹相似性度量

以包围面积作为度量依据.图1灰色部分是轨迹r1和r2的包围面积[7]，本文均是对起终点相同的两条轨迹进行比较，故所围区域闭合.

为统一量纲，将轨迹之间的平均距离表示为面积与较短轨迹长度的比值，即

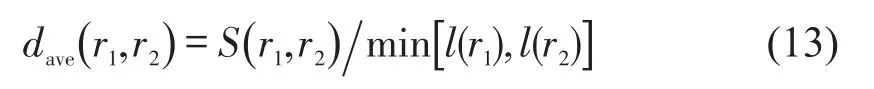
式中：dave(r1,r2)是两条轨迹间的平均距离；l(r1)，l(r2)分别表示r1,r2的长度；S(r1,r2)是r1与r2所围成的面积.dave(r1,r2)越小表示两条轨迹重合度越大，匹配概率越大.

图1 包围面积Fig.1 Boundary area

利用高斯核函数对距离指标值dave(r1,r2)标准化，得到轨迹相似度指标为

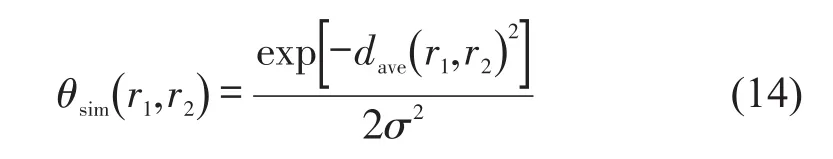
式中：θsim(r1,r2)是标准化后的轨迹相似度指标，θsim∈(0,1)；σ是带宽，控制原指标值的作用范围.θsim越大表示轨迹重合度越大，匹配概率越大.

图2为轨迹匹配成功后如何更新路线.设λ为轨迹相似度阈值，匹配规则如下：

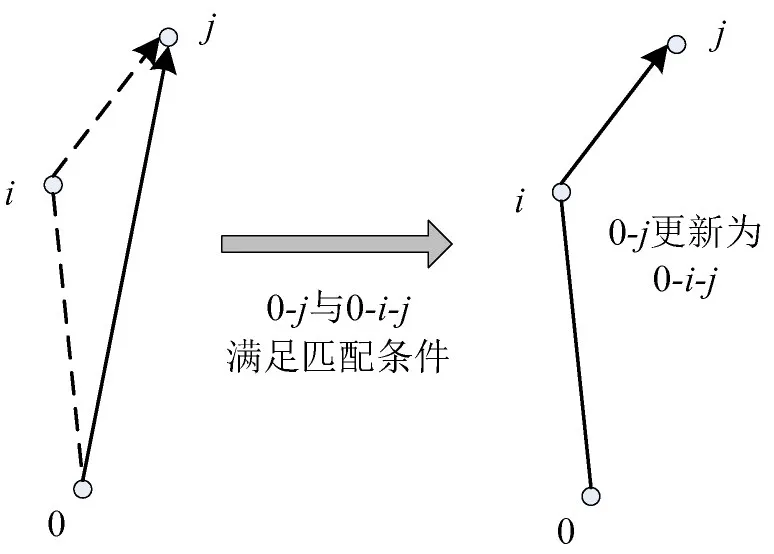
图2 路径更新Fig.2 Route update

(1)θsim(r0,j,r0,i,j)≥λ,需求i,j轨迹匹配成功，d0,j=d0,i+di,j,r0,j=r0,i,j.

(2)θsim(r0,j,r0,i,j)＜λ,需求i,j匹配失败.

2 算法设计

上述模型属于VRP(Vehicle Route Problem)，作为NP-hard问题，难以找到算法在多项式时间内解决.传统路网合乘问题可根据出租车原始行程作为基准来匹配附近可能的乘客需求，本文不具备该基准，使得乘客匹配可行组合数量庞大，并且车辆数作为目标函数增加了问题的复杂性.文献已证明聚类将大规模VRP问题分解成小规模子问题，再采用蚁群算法求解能够节省计算时间且求解结果更优[8]，因此将算法分为两阶段：

(1)乘客需求聚类.将乘客需求进行聚类以缩小优化的搜索范围.结果如图3所示.

(2)合乘匹配.使用双目标蚁群算法进行匹配优化.结果如图4所示.

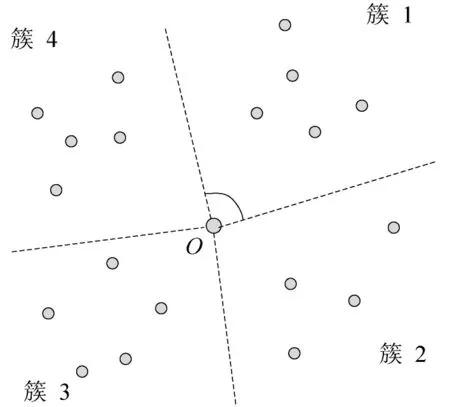
图3 聚类示意Fig.3 Clustering schematic

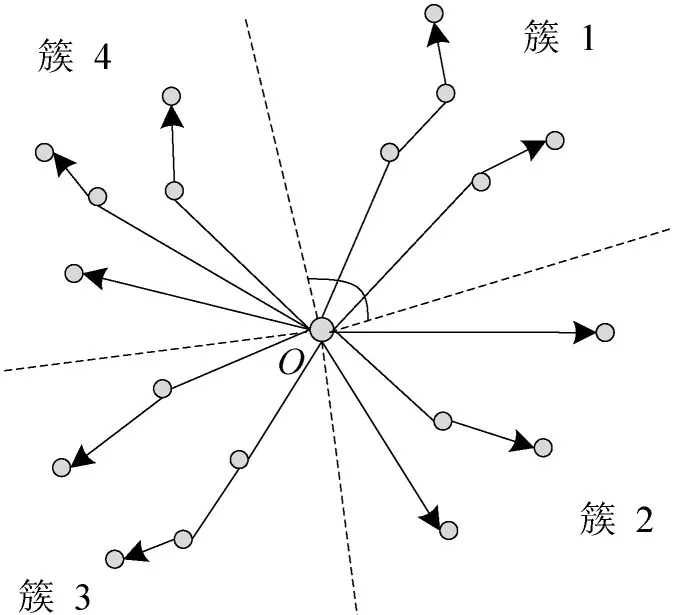
图4 匹配示意Fig.4 Matching schematic

2.1 需求聚类

行驶路径和时间窗是出行需求的核心组成要素.本文所有乘客的起点相同(枢纽站)，决定路径的是方向和终点.若乘客的路线方向相近，终点之间的距离对本文由近及远的行驶模式影响较小，因此选择(出发时间，方向角)向量进行聚类.设ω为终点方向角集合，ω={ω1,ω2,…,ωi,…,ωn}，ωi=(iy-Oy)(ix-Ox),ωi∈(-π,π),(ix,iy)是i的坐标，i∈ℕ+，(Ox,Oy)是枢纽站的坐标.k-mediods方法适用于低纬度聚类并能降低聚类对孤立点的敏感度，故使用该方法进行聚类，利用DB指标[9]来确定聚类数目.

2.2 双目标蚁群算法设计

聚类后每个簇需要进行匹配优化.蚁群算法对解决VRP系列问题有较好的性能.为加快收敛速度，用最近邻近算法得出可行解作为蚁群算法的初始解和初始信息素.

图5为匹配算法整体流程，Iiter为迭代索引，Iiter_m为最大迭代次数，Uupper为出租车需求数量的上限.搜索最短总里程的过程中，可能通过增加车辆数减少系统总里程，故先确定最优解出租车数量的上限，再对总里程进行优化.

图5 基于蚁群算法的匹配优化整体流程Fig.5 Matching optimization process based on ant colony algorithm

(1)初始解计算.

初始化信息素为

式中：δ0是初始信息素；L1是最近邻近算法得到的总里程.最近邻近算法为随机选择第1个需求点i，在剩余满足约束的需求点集合中，选择距离该点最近的需求点，以此类推，直到该车达到容量限制或者无需求点可选为止，增加一辆空车重复以上步骤，当所有点均被服务后计算所需车辆数||K和系统总里程L1.

(2)确定最优解出租车数量上限.

利用蚁群算法的初代确定出租车最优数量的上限，具体算法如下：

Input最近邻近算法计算所得，蚂蚁数量M，所有乘客需求信息①设置ACO所有参数,Uupper=|K|②form=1toM③ 蚂蚁m进行搜索④ if搜索成功 & 车辆数小于等于Uupper⑤ then⑥ Uupper=Uupper-1⑦ end if⑧end for OutputUupper

(3)信息素更新与转移规则.

信息素更新，选择每次迭代中的前两条最短路径所经过的a(i,j)进行全局更新.

转移规则，若每辆出租车第1位乘客的终点离枢纽较近能够加大后续匹配成功率，所以每增加一辆新出租车时，仅在剩余可供选择的需求集的前半部分产生第1个需求点.考虑时间窗越宽匹配概率越大，安排出租车去服务下一个需求点的转移公式为

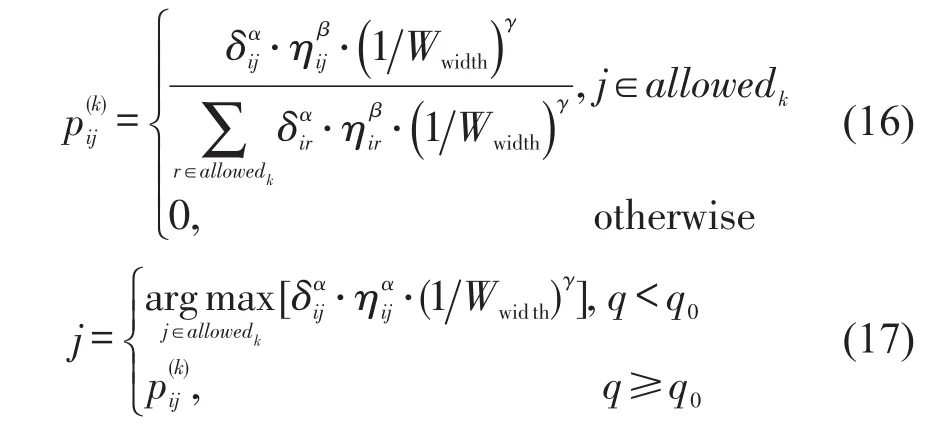
3 案例分析

3.1 数据准备

以北京南站为例，收集2019年3月15日22:00-23:00，在出租车调度站等候出租车乘客的需求信息，共计456条.包括终点目的地、到达出租车停靠点的时间，以及可接受最晚到达目的地的时间.部分数据如表1所示.

表1 部分乘客信息表Table 1 Partial passenger information

3.2 实验过程

不同聚类数所对应DB指标值如图6所示，当聚类数为13时达到拐点，此后聚类个数的增加所对应DB指标下降减缓.故将13作为目标聚类数目，聚类结果如表2所示.

图6 不同聚类数下的DB指标值Fig.6 DB values of different number of clusters

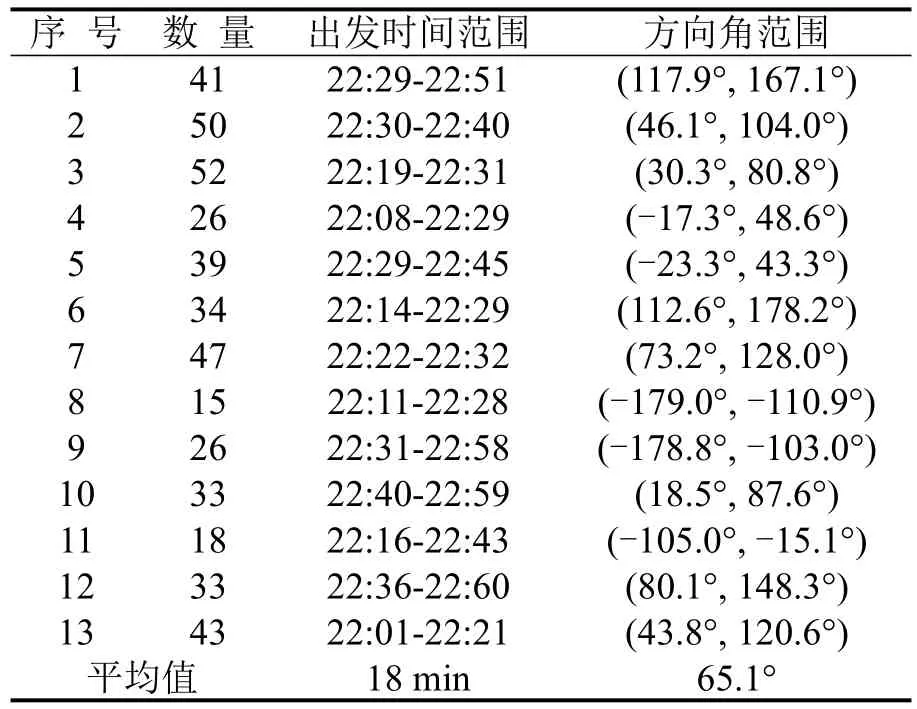
表2 聚类结果Table 2 Clustering results

聚类后，通过高德API获取簇中所有需求点的最短距离及最短轨迹矩阵，轨迹数据包括约578万条GPS坐标(取样1 s/条).为节约计算内存，利用Douglas-Peucker方法进行拐点识别简化轨迹[10].图7为北京南站至各终点的轨迹，以及终点之间的轨迹(以簇3为例)，轨迹中所有的道路拐点均被精确提取.

参数设置如表3所示，经灵敏度分析(3.3.1节)，阈值λ=0.9.利用MATLAB进行计算，得出分簇结果如图8和图9所示，整体结果如表4所示.

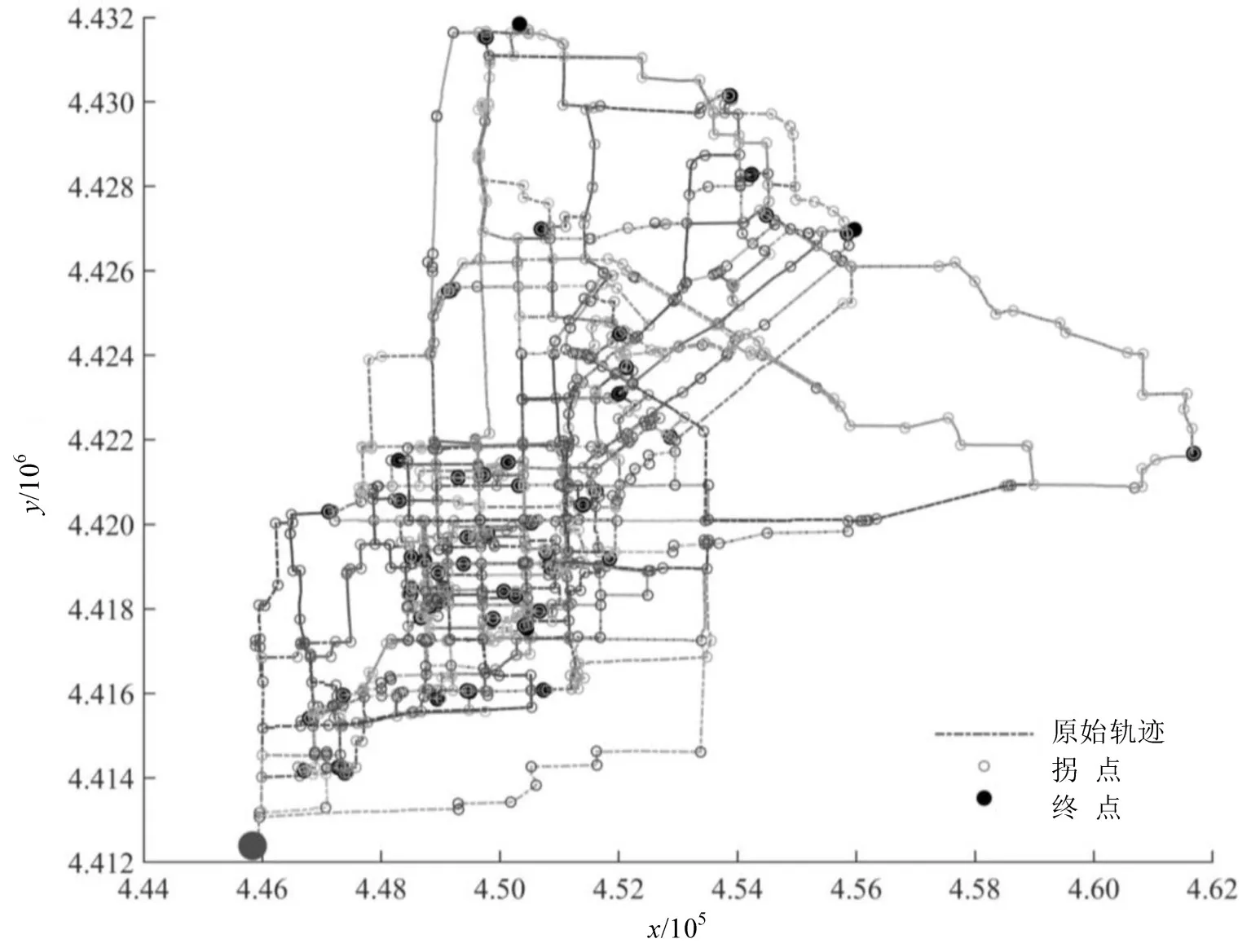
图7 簇3所有需求点轨迹及拐点识别Fig.7 All trajectories and inflection-points of cluster 3

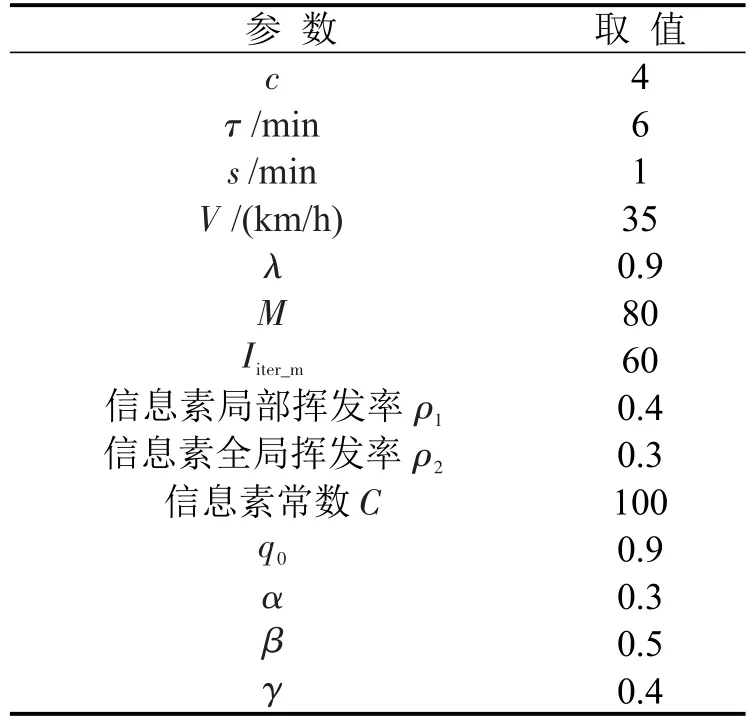
表3 参数设置Table 3 Parameter settings

3.3 实验结果分析

3.3.1 轨迹相似度阈值灵敏度分析

λ取值0.70～0.98时，目标函数总里程与车辆数的变化情况如图8所示，阈值越大，目标函数值越大.整体而言：λ取值在0.70～0.84时，对车辆数变化影响微弱，在145上下浮动，总里程小幅稳定增长；λ取值在0.92～0.98时，车辆数和总里程增幅均较大，此时λ对目标函数的影响程度较大；λ取值在0.86～0.90时，是车辆数和总里程数的拐点区域，在此范围内取值时，可保证绕行比例较小的同时避免目标函数增长过快.

3.3.2 结果对比

图9为λ=0.9时，各簇所需车辆数和节省里程比例.节省里程比例最高的是簇3，最低的是簇11，结合需求数量，簇3与簇11车辆数优化亦为最佳与最差.说明，各簇的匹配结果与其聚类情况关系紧密，簇中方向角和出发时间跨度越小匹配效果越好，反之亦然.

图10是乘客绕行比例箱线图，整体绕行比例较小；各簇的平均绕行比例低于1.1，75%乘客绕行比例小于1.2，最大为1.4，最小为1.0.本文方法能够有效减弱绕行情况.

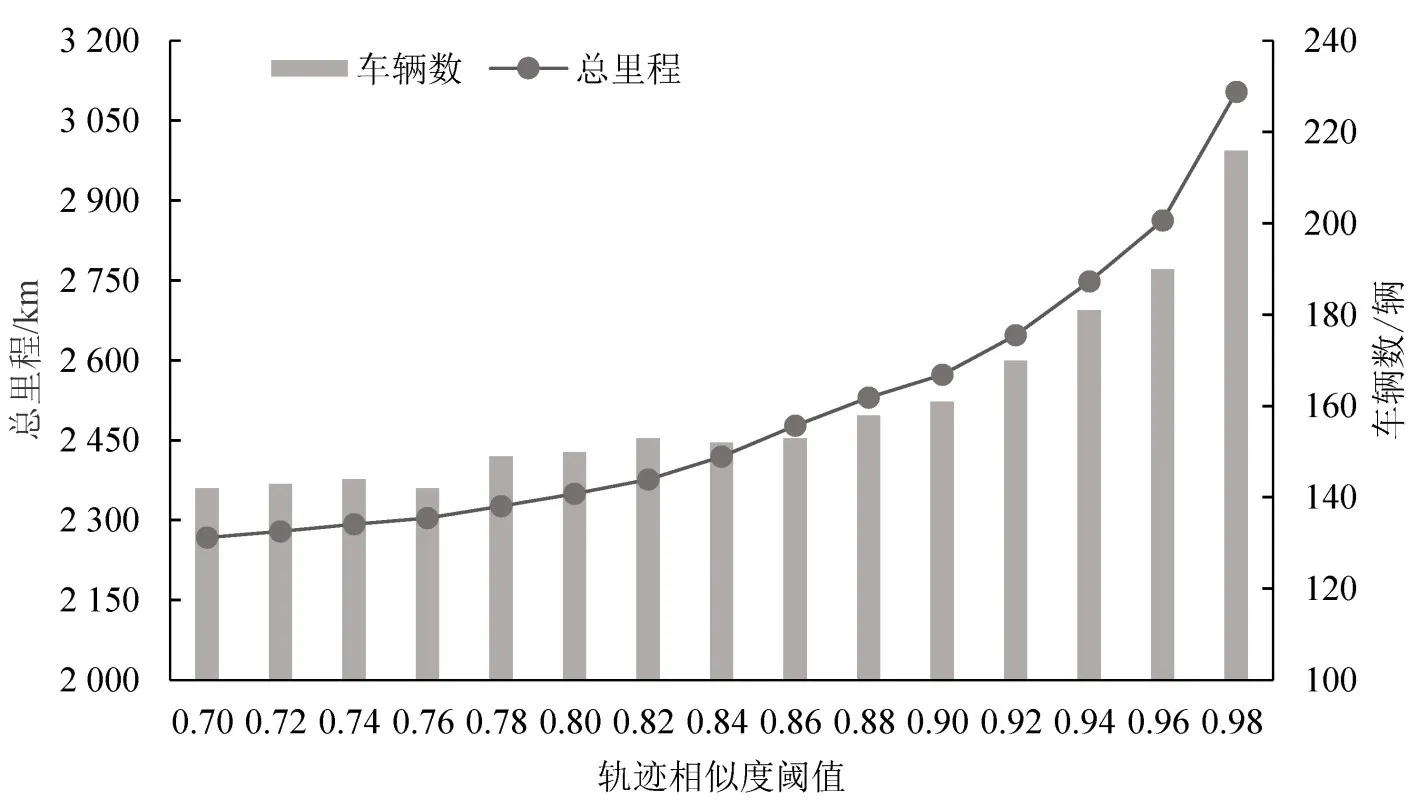
图8 轨迹相似度阈值灵敏度分析Fig.8 Trajectory similarity threshold sensitivity analysis

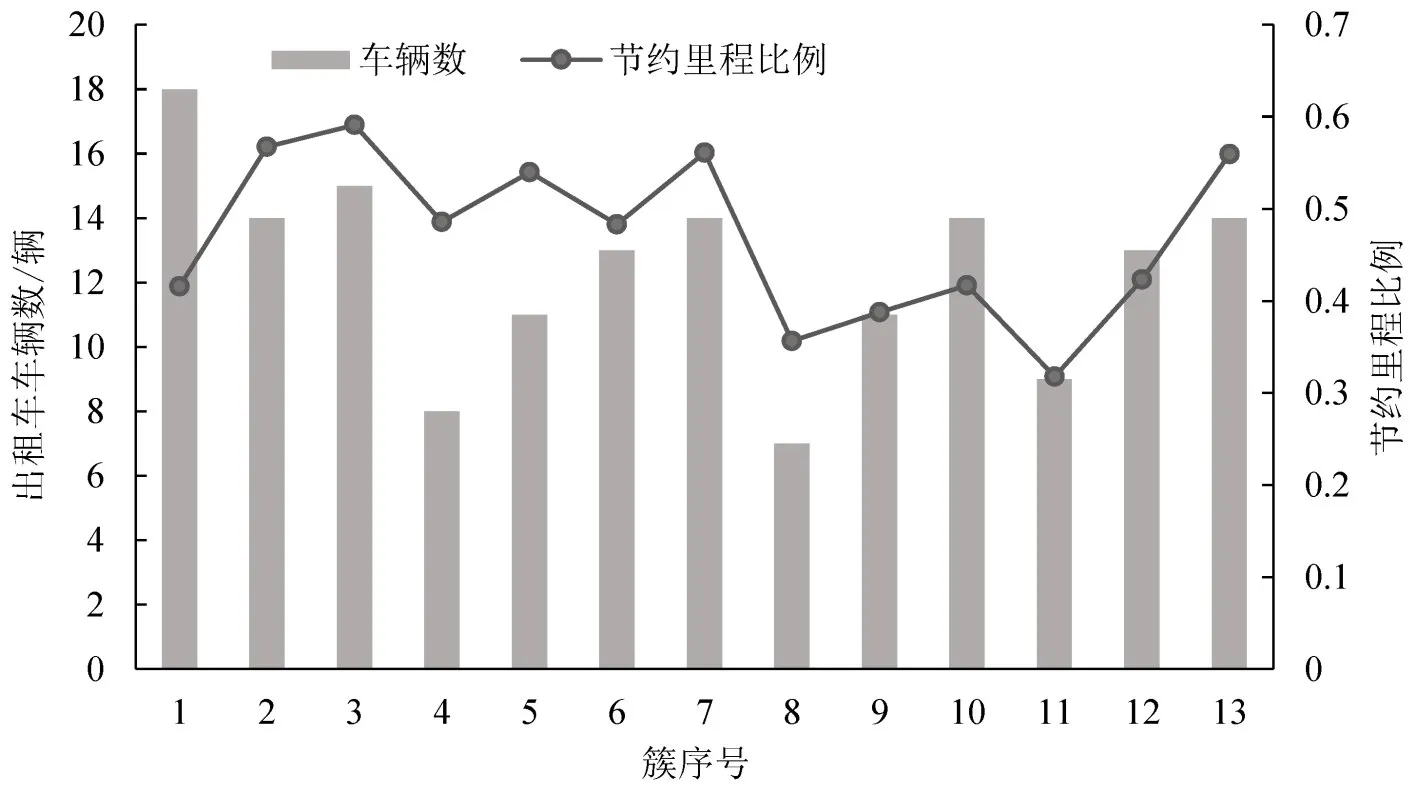
图9 各簇计算车辆数和节约里程比例Fig.9 Calculated number of taxis and saving mileage ratios for all clusters

图10 所有乘客的绕行比例箱线图Fig.10 Detour ratios boxplot of all passengers

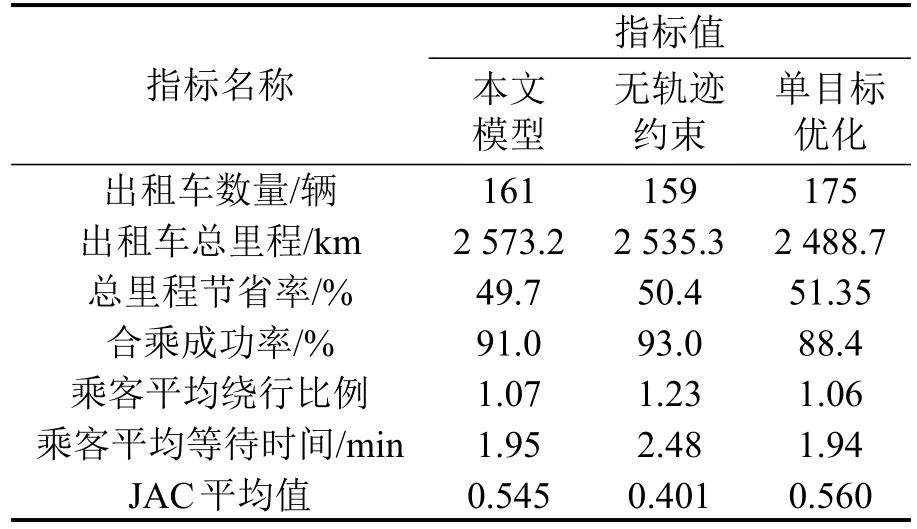
表 4 整体计算结果及对比Table 4 Overall results and compare

由表4可知：车辆数由合乘前的456辆缩减至161辆，合乘成功率为91%，总里程比合乘前缩减近50%；乘客平均绕行比例为1.07，等待时间为1.95 min.整体效果较好，集约系统资源的同时保障了乘客的利益.

将结果与无轨迹相似约束模型、单目标优化模型的结果进行对比.删去轨迹相似约束之后，车辆数和总里程有小幅降低，平均绕行比例增加至1.23.无轨迹形态要求略微提高了合乘成功率，但易使行驶路线绕行增加.

JAC指标旨在量化路段重合情况，计算公式[11]为

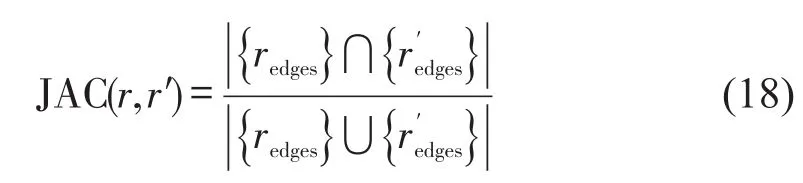
模型计算的JAC平均值为0.545，无轨迹相似约束计算出JAC平均值为0.401，说明添加轨迹相似度约束的合乘路径更接近乘客对行驶路径的预期.单目标优化中的目标函数是最小化行驶总里程.仅追求总里程最小时车辆数增加至175辆，比原有结果增加了8%，且乘客平均绕行比例、等待时间、JAC指标的结果改善甚微.说明双目标优化能在保证系统优化同时，缩减出租车使用规模.

4 结论

本文提出基于轨迹相似性度量的合乘匹配方法.在引入轨迹相似度进行约束，保证规划路径满足乘客心理预期的基础上，以最小车辆数和最少总里程为目标建立双目标优化模型.设计先聚类后匹配的两阶段算法进行求解.结果表明，经灵敏度分析，阈值在0.86～0.90时，能兼顾规划路线绕行比例较小及目标函数达到较优水平.对比其他方法，本文方法对优化车辆数和总里程有良好的效果，保证乘客等待时间较低，轨迹相似性度量约束能有效提高合乘后路径的JAC值.对出租车合乘发展有一定实践意义.