脑部电阻抗有限元模型的脑膜结构仿真

张 涛，安志伟，刘学超，章伟睿，代 萌，杨 滨，刘锐岗，徐灿华

（空军军医大学军事生物医学工程学系，西安710032）

0引言

电阻抗断层成像（electrical impedance tomography，EIT）是通过在目标体表施加一定的安全激励电流，利用体表测得的电压信号来重构其电阻抗分布的一种新型成像技术，在呼吸功能检测，脑、心、肺血流图，乳腺癌检测等领域已有临床研究[1-4]。电阻抗成像技术具有无创无害、连续性监护、成本低等特点，在颅脑损伤、脑卒中检测方面具有良好的应用前景[5-7]。有限元仿真技术是电阻抗研究的基础，可以有效评价电极干扰影响、噪声影响和成像算法性能[8-9]。有限元模型是有限元仿真技术的前提，有限元分析计算的精确性依赖于有限元模型的准确性。

国际上，Vonach 等[10]基于I-DEAS 软件利用MRI或CT 图像数据进行分割、表面提取、表面网格处理和网格剖分等步骤，快速构建了包含脑实质、脑脊液、颅骨和头皮真实解剖结构的4 层颅脑有限元仿真模型。前期，本课题组也利用Mimics、SolidWorks、COMSOL 等工具构建了一个3 层颅脑有限元模型，并基于COMSOL 与MATLAB 联合仿真实现了一帧电阻抗断层成像数据的快速仿真计算[11-12]。在此基础上，本课题组进一步构建了一个包含头皮、颅骨、脑脊液、脑实质和脑室的5 层结构模型，并在仿真研究中得到了较好的应用[13-14]。目前，脑部电阻抗有限元模型大都基于头皮、颅骨、脑脊液、脑实质等较大结构建立，没有考虑到细微结构的影响，为提高电阻抗成像技术在脑部应用的准确度，有必要进一步提高有限元模型的精确性。本文将针对脑膜结构，研究其对于电阻抗正问题计算结果的影响。在实际仿真中，若参照前期对CT 图像中脑膜结构进行分割、三维重建的方法构建含脑膜结构的模型，生成的三维脑部模型由于脑膜结构太薄，与脑实质等结构在几何尺寸方面存在较大差异，会导致无法成功剖分网格，或即使剖分成功但产生的网格数量巨大且质量较低，也难以用于有限元计算，因此脑膜结构仿真仍是难点问题之一。

基于此，本文拟提出一种近似模拟脑膜结构的脑部三维有限元仿真方法，在确保网格剖分成功的前提下降低模型复杂度，从而更加精确地模拟真实脑部结构，为课题组后续脑部精准模型的研究打下基础。

1 方法

1.1 电阻抗有限元仿真的数学基础

在电阻抗断层成像的测量中，设置激励源频率一般为10～100 kHz，此频率下介电常数的影响微小，基本可以忽略[15]。假定成像区域内部不存在电流源，且电导率分布具有各向同性，那么电阻抗断层成像的电磁场计算方程描述如下：

在目标区域Ω 内电位满足拉普拉斯方程：

其中，φ 为电位分布；σ为电导率分布。

在强加边界上满足：

其中，φ0为给定边界上的电位。

在自然边界上满足：

其中，Jn是给定边界上外加激励的电流密度，无注入时为零。

公式（1）～（3）是本文进行有限元仿真计算的基础。

1.2 薄层模型的定义

本研究中，将脑膜结构利用薄层结构进行替换，该薄层近似模型基于如下假设：切向方向的电流密度矢量分量非常小，在薄层结构中的传输主要由径向方向的r 分量构成[16]。因此公式（1）可以近似为

对公式（4）进行积分，可以得到：

其中，a 和b 是积分常数。如果薄层结构的上下表面电位分别为φ1和φ2，则电势的计算公式如下：

那么，结合电流密度定义可得到：

其中，Jr为径向电流，δr为薄层结构的厚度。

公式（7）可在COMSOL 软件中通过设定薄层结构属性实现计算。

1.3 脑膜薄层模型的构建

有文献报道了脑部三维有限元模型的构建方法，并进行了多项研究，原方法所建三维模型如图1所示[5]。在原建模方法的基础上，首先，将原脑部三维有限元模型导入到COMSOL 软件中，设置头皮、颅骨、脑脊液、脑实质和脑室等各层材料属性，定义一个数据选择集表示脑实质；其次，选定脑实质数据集，将脑实质的表面单元加入薄层中，在COMSOL软件中设定表面薄层边界条件，在薄层属性栏中设置表面厚度为0.2 mm，电导率设定为脑膜电导率0.065 S/m，相对介电常数为1，如图2 所示；最后，根据电阻抗断层成像电磁场计算方程，在COMSOL 软件中设置求解方程、激励电流和强制接地点等仿真计算条件及有限元剖分条件，完成剖分并进行有限元计算分析。

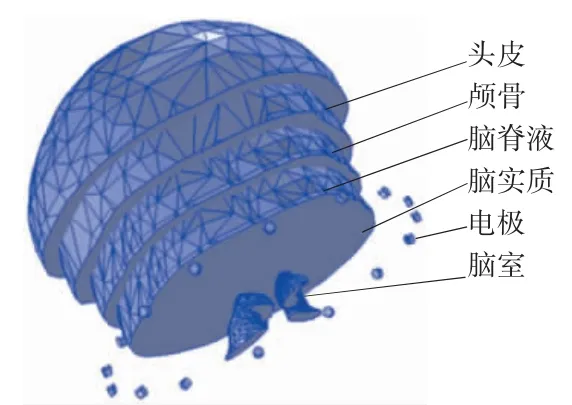
图1 原三维脑部模型

图2 选定脑实质表面单元构建脑膜薄层模型（单位：m）

1.4 有限元仿真计算分析

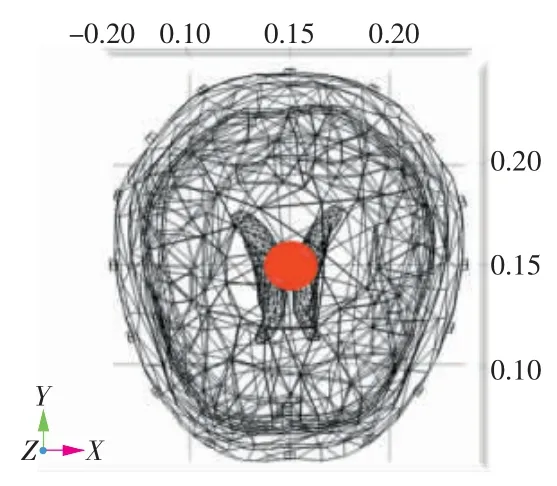
图3 出血灶目标设置位置示意图（单位：m）

为了验证建立的包含脑膜的脑部有限元模型能否进行有限元分析计算、探究脑膜结构对电势分布的影响，首先，参照电阻抗断层成像正问题中的边界条件设定对向激励电极的法向电流密度为±1 A/m2，求解脑部模型的电势分布和电流流向情况；其次，为避免位置因素对结果造成影响，按照图3 所示，在原三维模型中心处设置球形出血灶目标（电导率设为0.67 S/m）模拟出血情况，计算测量电极电位值；最后，在原三维模型中增加脑膜结构，计算测量电极电位值，对比增加脑膜结构与出血灶目标后对原三维模型电极测量电势结果的影响程度。

设φ原模型表示在原三维模型下得到的测量电极电位大小，设φ出血灶表示在原三维模型中设置出血灶目标得到的测量电极电位大小，定义二者电位的相对变化为

同理，设φ含脑膜表示在原三维模型中设置脑膜薄层结构后得到的测量电极电位大小，定义其与原模型电极测量电位的相对变化为

仿真所用计算机配置为Intel i7-8700 3.2 GHz 处理器，64 GB RAM，NVIDIA GeForce GTX1660 显卡。

2 结果

2.1 含脑膜结构的脑部有限元模型剖分结果

采用上述方法构建了一个包含脑膜的薄层优化脑部有限元三维模型，在该模型中，脑膜结构利用薄层结构进行优化代替并包含在脑实质层中，整个模型更加逼近人脑真实结构。设置剖分单元最大尺寸为10.700 mm，最小尺寸为0.781 mm，曲率因子为0.4，最大单元增长率为1.4，得到含脑膜结构的脑部有限元模型包含373 677 个四面体单元，平均剖分质量均达到0.66。剖分结果如图4 所示。

2.2 有限元仿真计算分析结果

利用本文所述含脑膜薄层结构的脑部有限元模型进行电阻抗断层成像正问题仿真，施加对向激励电流后，得到的表面电势分布和内部电流流向如图5 所示，可以看出，电势和电流分布从正向到负向变化明显，仿真结果与实际相符，该模型可以进行有限元计算。

在模型中心位置设置3 和5 ml 出血灶目标模拟脑组织发生病变，利用上述方法计算电极测量电位相对变化，结果如图6 所示。由图6 可以看出，加入5 ml 出血灶目标对电极电位的影响较大，而加入脑膜结构与加入3 ml 出血灶目标对测量电极电位的影响几乎一致。由此可见，加入脑膜结构与中心位置设置3 ml 出血灶目标会对电极测量电位值产生同等水平的影响。

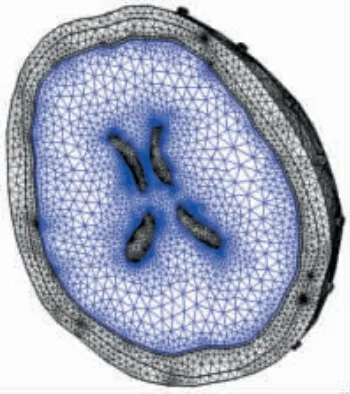
图4 含脑膜结构的脑部有限元模型剖分结果

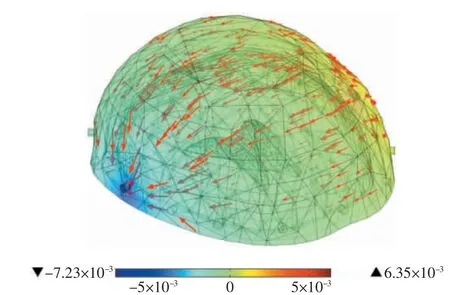
图5 表面电势分布和电流流向示意图

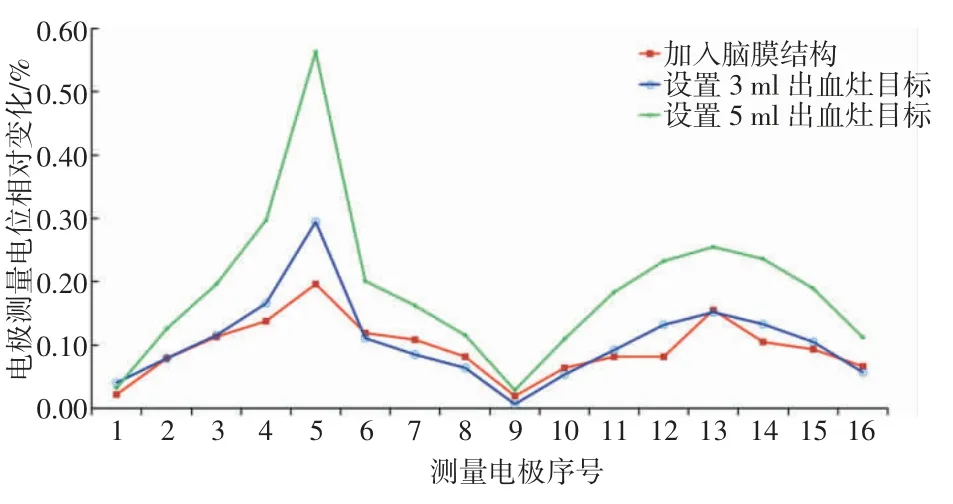
图6 电极测量电位相对变化曲线

3 结语

本文实现了一种利用薄层结构近似模拟脑膜结构的脑部有限元模型建模与仿真方法，使得脑部有限元模型的准确性得到了进一步提升。从仿真计算结果来看，本文的方法操作简单，可以在确保模型剖分成功的情况下，减少剖分薄层结构模型的复杂度，同时可以近似模拟脑膜结构低电导率带来的阻抗效果。通过与设置出血灶目标模型对电极测量电位值产生影响的对比，可得到加入脑膜结构与在中心位置设置3 ml 出血灶目标会产生同等水平的测量电极电位变化，进一步说明了研究精确模型的必要性。

然而，本文的仿真方法仅适用于电导率较低的薄层组织仿真中，对于导电性较好的薄层组织该方法不适用，具有一定的局限性。此外，本文的模型中脑脊液、脑室结构与真实的解剖结构还存在一定差异。下一步，将构建更加符合真实脑脊液整体解剖结构的有限元模型，评价脑脊液结构对电阻抗成像的影响。