反应堆压力容器顶封头接管冷装过盈配合力学分析

金东杰,郭 平,张 焱,金 刚，马斓擎

(1.中核能源科技有限公司，北京 100193；2.生态环境部 核与辐射安全中心，北京 102445)

0 引言

200 MW低温核供热堆反应堆压力容器的壳体由低合金钢锻件在内表面堆焊不锈钢制成，与壳体连接的各种奥氏体不锈钢小口径接管主要采用冷装过盈配合加密封焊连接方式。冷装过盈配合加密封焊结构，采用过盈配合来承受机械载荷、压力载荷等外载荷，同时由密封焊保证压力容器的密封，这种连接能有效地减少压力容器壳体上的贯穿性焊缝。

过盈连接广泛应用于机械连接中，用来传递轴向力和扭矩。GB/T 5371—2004[1]介绍了机械连接中过盈配合的计算和选用方法，但对于受内压的容器，该方法没有考虑施加内压后开孔处的变形对过盈配合的影响，不能直接用于压力容器接管过盈连接的计算。有学者[2-3]研究了过盈量对结合面应力的影响，但未给出最小和最大过盈量的计算方法以及内压、温度及接管外载荷对过盈量的影响。

为确定接管与封头壳体冷装过盈配合结构合理的最小过盈量和最大过盈量，本文以200 MW低温核供热堆反应堆压力容器顶封头壳体与接管间的过盈配合为例，通过理论分析分别确定冷态工况下接管外径与壳体开孔处最小和最大过盈量计算的适用工况；并通过简化模型的解析解推导出过盈量的工程计算方法；再通过有限元分析验证冷态工况工程计算方法的合理性和热态工况下热应力对过盈配合结构的影响。

1 接管与封头的连接形式

反应堆压力容器壳体材料为SA508，接管为316奥氏体不锈钢，接管与封头的连接形式如图1所示。

图1 接管与封头的连接结构示意

2 冷态工况过盈配合连接的过盈量计算

2.1 计算模型

对冷态工况下的接管与壳体间的过盈配合连接，以两个简单厚壁圆筒在弹性范围内的连接为计算基础，并建立如下力学模型：

(1)接管简化为受外压的刚性圆筒；

(2)由于接管开孔内径远远小于球形封头壳体内径，将壳体简化为开孔处受内压的当量圆筒；

(3)当球形封头受内压作用时，接管视为同时受外压和内压的刚性圆筒，壳体所简化的当量圆筒应同时叠加球形封头因受内压而产生的薄膜应力所引起的开孔变形。

假定接管和壳体过盈连接时均在弹性范围内。弹性范围[1]指接管和壳体由于结合面压力而产生的变形与应力呈线性关系，即连接结构的应力低于接管和壳体材料的屈服极限。由此，对接管与壳体过盈连接的直径变化量可通过弹性力学平面应力问题的应力应变关系计算得出，根据弹性力学相关理论作如下假设：

(1)接管与壳体处于平面应力状态；

(2)接管与壳体在结合长度上结合压力为常数；

(3)材料的弹性模量为常数。

2.2 最小和最大过盈量计算的适用工况

冷态工况下，接管和壳体的过盈连接结构分为壳体不承受内压的装配工况和壳体承受内压工况。内压工况下，内压会对壳体产生薄膜应力，导致壳体开孔处直径变大，进而使过盈配合在承受内压后过盈量减小；而对于接管，内压作用下接管为外壁承受结合面外压，内壁承受内压的刚性筒，加压后接管外径变大，进而使过盈配合在承受内压后过盈量增加，但与壳体薄膜应力引起的开孔直径变化相比，接管内压引起的接管外径变化远小于开孔直径变化。为简化计算，工程计算时保守考虑，忽略内压对接管直径变化量的影响，只考虑内压引起的壳体薄膜应力对开孔直径变化的影响，进行过盈配合的最小过盈量计算。过盈配合连接结构应能承担水压试验压力下接管的最大拉脱力，当压力容器承受设计压力但最初运行温度未上升时，保守考虑过盈连接应能同时承担设计压力和管道外载荷引起的最大拉脱力。拉脱力是由接管与壳体结合面压力产生的摩擦力来承担的，由此根据以上两种工况下的最大拉脱力可以计算出接管与壳体过盈配合连接处结合面的最小压力，再通过弹性力学理论的应力应变关系，可以推导出过盈配合的最小过盈量的解析解。

由于内压减小了接管和壳体间的过盈配合量，接管和壳体的过盈连接在装配工况下过盈量最大，此时最容易引起接管或壳体材料的屈服。因此，应在装配工况下计算过盈配合结合面最大压力，进而通过弹性力学理论推导出过盈配合的最大过盈量的解析解。

接管和壳体间过盈配合连接结构的最小和最大过盈量计算时，适用的工况如表1所示。

表1 最小和最大过盈量计算时的适用工况

2.3 最小过盈量计算

2.3.1 接管最大拉脱力工程计算方法

由第2.2节工况分析可知，接管与壳体间的过盈配合连接结构应能承担内压工况下接管的最大拉脱力。水压试验和设计压力工况下接管的最大拉脱力工程计算方法分别如下。

(1)水压试验工况下接管的拉脱力。

水压试验作用下，接管所受的轴向力:

(1)

式中Do——接管外径，mm；

pT——压力容器的试验压力，MPa。

(2)设计压力工况下接管的最大拉脱力。

在压力容器设计压力作用下，接管所受的轴向力:

(2)

式中pD——压力容器的设计压力，MPa。

假定接管外载荷施加在接管外端面，分别为轴向力F外x，剪切力F外y,弯矩M外和扭矩N外，接管的外伸长度l外。

忽略平衡力的影响，将接管的剪切应力简化为对接管根部的弯矩,并与接管外载荷弯矩M外进行合成，则总弯矩：

M外e=F外yl外+M外

(3)

为便于计算，在计算接管轴向拉脱力时，将总弯矩简化为接管内部的当量压力，则如下式[4]：

(4)

式中Di——接管内径，mm。

则接管所受的总轴向拉脱力：

(5)

扭矩对接管与壳体过盈配合面产生的周向力：

(6)

将接管的轴向力、周向力进行合成，则:

(7)

2.3.2 过盈配合结合面最小结合压力

接管的拉脱力是由接管与壳体过盈配合结合面压力产生的摩擦力Ff来承担的，当接管不拉脱时，则有下列不等式：

Ff=p结πDolfμ≥F

(8)

式中lf——过盈配合长度，mm；

μ——摩擦系数。

由式(8)可得过盈连接结构承受最大拉脱力F时结合面所需的最小结合压力：

(9)

2.3.3 接管的外径最小变化量

根据第2.2节分析，忽略接管内压对接管外径变化量的影响，则接管为只承受外压p结min作用的刚性筒，根据弹性力学理论[5]的应力应变关系，对于平面应力问题，接管的径向应变为：

(10)

式中E1——接管材料在室温下的弹性模量，MPa；

σr1——刚性筒的径向应力，MPa；

υ1——接管材料的泊松比；

σθ1——刚性筒的周向应力，MPa。

由拉美公式求出σr1,σθ1(具体表达式省略)代入式(10)，可得接管外壁结合面处的直径最小变化量：

(11)

式中K1——接管的外径与内径之比，即

K1=Do/Di。

2.3.4 壳体开孔直径最小变化量

当球形封头壳体承受内压p时，根据球形壳体中径公式，可得壳体承受内压下的薄膜应力：

(12)

式中D球——球形封头的内径，mm；

δ球——球形封头的壁厚，mm。

球壳内压作用下的薄膜应力方向与封头切向重合，球壳在封头切向(直径D′方向，如图2所示)的变形量：

(13)

式中E2——壳体材料在室温下的弹性模量，MPa；

α——接管开孔处法线与设备轴线间的夹角，(°)；

υ2——壳体材料的泊松比。

图2 壳体开孔示意

则接管内径方向的直径变化量：

(14)

由内压厚壁圆筒的拉美公式并叠加封头薄膜应力引起的接管径向方向的直径变化量，根据弹性力学理论的应力应变关系，对于平面应力问题，求得壳体开孔直径变化量：

(15)

式中K2——厚壁圆筒的外径与内径之比，即

K2=D2/Do；

D2——壳体当量外径，mm。

(16)

2.3.5 最小过盈量

接管和壳体过盈配合的最小过盈量计算公式为：

δmin=δ1min+δ2min

(17)

2.4 最大过盈量计算

2.4.1 过盈配合结合面最大结合压力

(1)接管不发生塑性变形时的最大结合压力。

装配工况下，接管承受由过盈配合连接结合面压力p结1而产生的外压时，接管内壁处的应力强度最大[6]。根据拉美公式可知，接管的内壁处的径向σr1内、环向σθ1内和轴向σz1内三向应力分别为：

σr1内=0

(18)

(19)

(20)

由式(18)～(20)可知，σr1内>σz1内>σθ1内,则根据第三强度理论，接管内壁的等效应力强度为：

σ1max=σr1内-σθ1内

(21)

将式(18),(19)代入式(21)，得:

(22)

则接管不产生塑性变形时，可得下列不等式：

(23)

式中σs1——接管在室温下的屈服强度，MPa。

接管不产生塑性变形时，所允许的最大结合压力为：

(24)

(2)壳体不发生塑性变形时的最大结合压力。

装配工况下，当封头壳体开孔处承受结合面压力p结2时，壳体开孔部分可视为受内压的当量厚壁圆筒，圆筒内壁处的应力强度最大[7]。根据拉美公式，开孔内壁处的径向σr2、环向σθ2和轴向σz2三向应力分别为：

σr2=-p结2

(25)

(26)

(27)

σθ2=p结2

(28)

σz2=0

(29)

由式(25)，(28)和(29)可知，σθ2>σz2>σr2,根据第三强度理论，壳体开孔处的最大应力强度：

σ2max=σθ2-σr2=2p结2

(30)

则壳体不产生塑性变形时，可得下列不等式：

σ2max=2p结2≤σs2

(31)

式中σs2——壳体在试验温度下的屈服强度，MPa。

则壳体不产生塑性变形时所允许的最大结合压力为：

(32)

接管与封头过盈配合连接不产生塑性变形的最大结合力：

p结max=min{p结1max,p结2max}

(33)

2.4.2 接管的外径最大变化量

根据弹性力学理论的应力应变关系，对于平面应力问题，根据第2.3.3节接管的径向应变分析，可得外压为p结max时接管的外径变化量为：

(34)

2.4.3 壳体开孔直径最大变化量

根据弹性力学理论的应力应变关系，对于平面应力问题，根据第2.3.4节当量圆筒的径向应变分析，可得内压为p结max时当量圆筒的内径变化量为：

(35)

2.4.4 最大过盈量

接管与壳体过盈配合不产生塑性变形所允许的最大过盈量为：

δmax=δ1max+δ2max

(36)

2.5 反应堆压力容器封头典型接管过盈量计算

选取安全阀管嘴、控制棒驱动机构管嘴和氮气管嘴为例，对接管与反应堆压力容器顶封头的过盈连接结构进行冷态下的过盈量计算。安全阀管嘴、控制棒驱动机构管嘴和氮气管嘴的结构尺寸如表2所示。

表2 典型接管结构尺寸

安全阀管嘴、控制棒驱动机构管嘴和氮气管嘴接管端面外载荷如表3所示。

表3 典型接管外载荷

根据以上计算方法对典型接管进行计算，得出接管的过盈量如表4所示。

表4 典型接管过盈量 mm

接管的最小过盈量一般由设计内工况决定，通过计算结果可知：

(1)接管外径越大，结合面压力对接管和开孔直径产生的变化量也越大；外内径比也直接影响接管刚度，外内径比越大，直径变化量越小;

(2)直径变化量除了与开孔直径有关外，还与其配合的接管刚度有关，控制棒驱动机构管嘴虽然开孔更大，但接管外内径比小、刚度较低,所以壳体开孔直径变化量也相对较小，当接管刚度比接近时，开孔直径越大，直径的变化量也越大;

(3)壳体的最小直径变化量，由内压工况计算所得，由于壳体承受内压而产生的薄膜应力影响，壳体开孔处的直径变化量明显大于接管的直径变化量。

2.6 有限元分析验证

通过有限元分析，分别在最小过盈量和最大过盈量下进行典型接管和壳体开孔的接触分析，进一步验证理论分析的合理性。

2.6.1 有限元模型

图3 有限元模型及网格划分

典型接管和封头壳体冷装过盈配合连接有限元模型主要由壳体和接管组成。对密封焊区域加以简化，模型中仅模拟接管与封头壳体的过盈配合，为减少有限元网格划分规模，仅对封头进行1/4模型建模，之后分别对安全阀管嘴、控制棒管嘴和氮气管嘴在封头上进行全尺寸建模，并对接管与壳体过盈连接处网格划分进行细化，以安全阀管嘴为例的模型及网格见图3。

2.6.2 边界条件与加载

在模型两个对称面截面上施加对称边界条件。壳体和接管环境温度为22 ℃。为防止整个结构在有限元分析时刚体漂移，在法兰密封面施加轴向约束。在壳体内表面、接管内表面施加压力载荷,接管端部施加等效应力和接管外载荷。

2.6.3 分析结果

选取接管和壳体开孔接触部位危险截面最大厚度方向分别进行线性化处理，得到最大薄膜应力和薄膜+弯曲应力评定如表5，6所示。

表5 一次薄膜应力强度评定

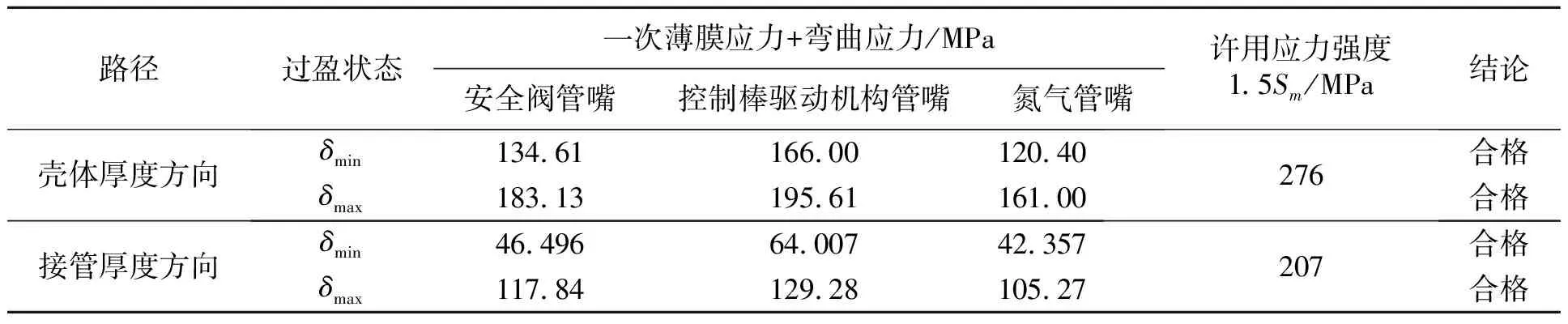
表6 一次薄膜+弯曲应力强度评定

结果表明，接管和壳体在最小过盈状态和最大过盈状态下，应力强度评定合格。

3 使用工况的过盈配合连接应力校核

使用工况下，反应堆压力容器除施加工作压力外，一回路冷却剂温度升高，壳体和接管本身同时承担相应的温度载荷。对于接管与壳体间的过盈连接结构，由于接管与壳体材料的线性膨胀系数不同，在过盈连接处就会产生热应力，同时使连接结构的过盈量增大，此时材料可能会进入局部屈服。热应力[8]是由于接管与壳体在自由状态下的变形不一致，由于约束条件而产生的应力。一旦构件发生局部的塑性流动，解除或部分改变了约束条件，其增长就受到限制，甚至还会下降，这种应力性质称自限性。热应力属于二次应力，应力校核时只需将一次加二次应力强度限制在3倍许用应力强度内即可。

3.1 模型及边界条件加载

采用ANSYS有限元分析软件对第2.5节中反应堆压力容器封头过盈配合的典型接管，在使用工况下施加热应力载荷后的应力强度进行校核。有限元模型建立、网格划分及载荷和边界条件施加与第2.6节类似，只不过在施加载荷时增加温度载荷。

3.2 应力结果及评定

对每对过盈连接面，选取过盈连接处壳体厚度和接管厚度方向的危险截面处分别设置路径，应力强度评定结果如表7所示。

表7 应力强度评定

结果表明，接管和壳体在热态工况下应力强度评定合格。

由表7可知，反应堆因停堆或大修降温后，部分接管局部会进入塑性变形，而壳体尚在弹性范围内，未进入塑性变形，这时接管降温后外径尺寸可能会大于原尺寸，但这增加了过盈配合量，有利于接管与壳体的连接，连接结构不会发生过盈松弛。

4 结论

(1)冷装过盈配合可以有效减少反应堆压力容器贯穿性焊缝，从而最大程度地减少异种钢焊接量，进而减少异种钢焊接带来的焊接裂纹等一系列问题。

(2)接管与封头壳体过盈配合连接结构的最小和最大过盈计算时，应全面考虑各种工况，并找出对应的合理计算工况，才能既保证接管极限工况不被拉脱，又能使材料满足强度要求。

(3)文中给出的冷态工况下接管最小和最大过盈量的工程计算方法简便、快捷，有限元分析也表明过盈配合连接结构强度满足要求，进而验证了工程计算方法的合理性。

(4)在热态工况下，有限元分析结果表明热应力对过盈连接的作用会导致连接结构的局部屈服，但不会造成结构的整体破坏，过盈配合连接结构强度校核合格。

(5)本文方法可为压水堆或其他类似结构的过盈配合连接设计提供参考。