基于局部法定量表征面外拘束效应对转变区间断裂韧度的影响
张亚林,惠 虎,周忠强,丛湘纯,胡馨丹
(华东理工大学 机械与动力工程学院,上海 200237)
0 引言
机械结构的脆性断裂是最为危险的一种失效模式,获取低温脆性条件下压力容器与承压管道的断裂韧度在断裂力学评估中尤为重要[1]。然而对承压结构常用的铁素体类钢来说,在低温下的断裂韧度呈现出本质的分散性。近30年的发展,在定量描述铁素体类钢在转变区间的断裂韧度方面已经取得了重大的发展。标准ASTM E1921(主曲线法)仅需要通过少量的试验,由一个参考温度T0就可以描述整个转变区间不同失效概率下的断裂韧度[2]。为了得到有一定安全裕量的评价结果,标准中要求被测试样高度拘束,也即是要有足够的面内和面外尺寸来保证试样裂纹尖端处于高的拘束状态[3]。
拘束可以理解为结构对裂纹尖端塑性变形的阻碍,拘束问题一直是国内外研究的热点[4-7],其中的研究思路大致分为两类:一类是基于宏观整体载荷参数(JⅠc,KⅠc和COD),如Williams的K-T理论[8],O′Dowd的J-Q理论[9]和Yang的J-A2理论[10]等;另一类是基于细观损伤/断裂力学局部法模型[11],纳入了裂纹尖端断裂过程区的实际的应力应变,因而局部法自然地容纳了拘束对裂纹场和材料损伤断裂行为的影响[12]。局部法相对于整体法来说是一种自下而上的研究方法。
Irwin[13]的研究表明试样的厚度剧烈地影响试样的表观断裂韧度,随着厚度的增加断裂韧度逐渐减小,直至达到平面应变应力状态断裂韧度出现一个下平台。Yang等[14]研究了不同的拘束参数和断裂韧度的关联,比较了不同拘束参数的适用性,并提出一个统一的拘束参数Ap可以灵敏响应面内外拘束程度的变化。宏观断裂参数可以通过关联拘束参数解决延性断裂问题,但是低温断裂韧度的本质分散性,关联拘束参量和断裂韧度是很难实现的。实际上,许多部件具有小的面外拘束(小的厚度),这会有效地增加部件的表观断裂韧度。由于脆性断裂下拘束效应的复杂性,面外拘束的降低对脆性断裂的影响还没有定量化的理解。本文通过标定局部法模型,对系列厚度下SEB试样进行有限元模拟,研究厚度效应对主曲线法参考温度T0的影响,并定量表征裂纹前缘的长度和T0的关系。
1 材料与力学性能试验
1.1 材料
本文使用课题组内正火态厚度40 mm的Q345R热轧板和试验数据作为研究对象[15],利用3种不同裂纹配置(PCVN,0.5T-SEB,1T-SEB)的三点弯曲试样标定,并验证局部法Beremin模型。根据威布尔(Weibull)参量的尺寸无关性,运用韧性换算思想将低拘束的PCVN断裂韧度换算成高拘束的1T-SEB试样,通过主曲线法比较换算后的参考温度和基于实测的参考温度,以检验韧性换算思想的可靠性。在此基础上,通过局部法预测系列面外拘束的变化对主曲线参考温度T0的影响。
Q345R钢的化学成分见表1。-100 ℃时真应力-真塑性应变见图1[15],其中屈服强度429.3 MPa,弹性模量220 959 MPa。

表1 Q345R钢的化学成分

图1 Q345R在-100 ℃时的真应力-真塑性应变曲线
1.2 断裂韧度测试与分析
断裂韧性试验方法和数据分析过程参考ASTM E1921和ASTM E1820,标准试样1T-SEB,0.5T-SEB和PCVN试样都是沿着T-L方向取样,名义疲劳裂纹深度比a0/W≈0.5。断裂韧度试验结果和主曲线法的分析结果见表2。其中KJc(limit)是为了保证裂纹尖端的高拘束状态,其表达式见式(1)。试验值小于KJc(limit)才是合格试样,高于该限值时,一般将KJc(limit)代入公式计算。本文运用多温度法计算主曲线法参考温度T0,其中多温度法的迭代方程见式(2),通过Matlab编程迭代计算得到。
(1)
式中b0——初始韧带尺寸,mm;
σys——试验温度下的屈服应力,MPa;
E——弹性模量,GPa;
Mlimit——试样的无量纲变形程度,标准ASTM E1921规定无量纲变形极限Mlimit=30;
υ——泊松比。
(2)
式中Ti——对应于各KJc(i)的试验温度,℃;
δi——检查常数,当KJc(i)有效,δi=1;当KJc(i)无效,δi=0。

表2 主曲线法断裂韧度分析结果
从表2可以得到三种类型试样的参考温度为-63,-111,-120 ℃。相比于1T-SEB试样的参考温度结果, 0.5T-SEB和PCVN试样的结果降低了48 ℃和57 ℃,且PCVN试样有效试样的数目不满足ASEM E1921中的有效性要求。尽管这些试样都是ASEM E1921中允许的试样,但是测试结果偏差如此之大,可以总结出两个问题:(1)变形控制参量Mlimit会导致绝大多数试样都不合格,如PCVN试样,这就很难达到标准中有效试样数目的要求(至少6个);(2)即使有变形控制参量Mlimit,也会让一些低拘束试样产生过高的韧性估计,如0.5T-SEB,这种现象尤其对于低强度钢更为常见。可见ASTM E1921对于低温断裂韧度的拘束方面的要求和限定还不够完备。局部法作为一种细观力学断裂模型,基于裂纹尖端的实际应力应变的Weibull应力可以有效地解决低温断裂的拘束问题。R6从第三版开始以附录的形式收录了Beremin模型。
2 局部法模型与威布尔参量标定
2.1 局部法模型简介
按照最弱链理论,Beremin假定断裂过程区是由大量的统计上相互独立的微元体组成,当微元体的体积足够少时,可以忽略微元体处的应力梯度,故微元体可视作为受均布载荷σ1作用,如图2[16]所示。并用两参数的Weibull分布来描述解理断裂的失效概率,见下式:
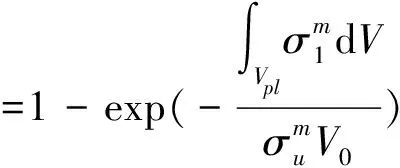
(3)

式中Pf(σw)——累积失效概率;
σw——解理断裂的驱动力,MPa;
Vpl——断裂过程区,为满足下式的单元体积:σ1≥λσys;
λ——大于或等于1的常数;
m——Weibull斜率;
σu——Weibull参量,对应失效概率为63.2%的σw,MPa。
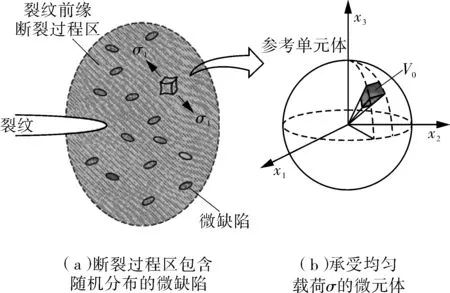
图2 Beremin模型裂纹尖端缺陷假定
2.2 有限元建模与Weibull参量标定
(m,σu)称为Weibull参量,它需要通过实测一系列断裂韧度数据,然后通过一定的程序标定获得,经典的标定法为Minami标定法[17]。但这种单试样标定方法已被很多的研究证实无法准确标定。现在国际上比较认可的方法是通过高低两种不同拘束程度的试样进行标定,如文献[16,18]提出的GRD标定法,RGD标定法等。所谓威布尔参量的标定,就是找到一组合适的(m,σu)通解,使其能够准确描述小尺寸试样和大尺寸试样解理断裂发生的累计失效概率,也即是对特定失效概率下大/小尺寸试样具有相同的解理断裂驱动力。文献[19]中研究的交点法可以有效并且简单地完成Weibull参量的标定。本文以0.5T-SEB和PCVN韧性数据作为标定数据,借助于Matlab编程和ABAQUS商用有限元软件进行参量标定。

图3 典型三点弯曲试样
对三种不同裂纹配置的试样进行三维弹塑性有限元分析。由于试样的结构和载荷的对称性采用1/4模型建模,模型的边界条件施加在对称面及韧带上。模型单元采用限行减缩积分C3D8R单元,以根部半径为0.002 mm的半圆作为裂纹尖端,并验证了网格无关性,模型和局部网格如图3所示(图中,RP为加载的参考点)。J积分的计算设置了20条积分回路,验证了J积分路径无关性,并取远场第20条回路计算J积分。
通过Matlab自编程序求解的交点法见图4,具体的求解过程见参考文献[19]。标定过程中式(3)中参考体积取V0=1.25×105μm3,得到m=8.2,σu=5 232 MPa。下文将比较试验结果和预测结果,以验证局部法参量标定的正确性。
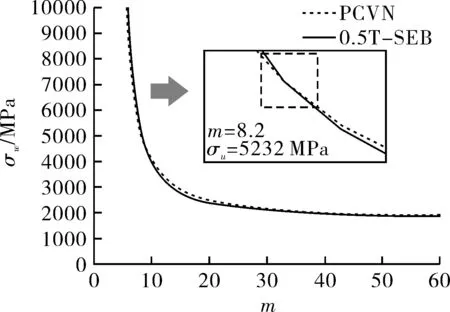
图4 交点法标定Weibull参量
2.3 Weibull参量及韧性换算有效性验证
根据Weibull参量的尺寸无关性,可以预测任意结构的参考温度T0,从而可以定量表征面外拘束的变化对断裂韧性的影响,预测流程图见图5。在这个过程中既需要保证威布尔参量的有效性,同时又要实现不同结构之间韧性可以换算,以下针对这两点分别进行研究。
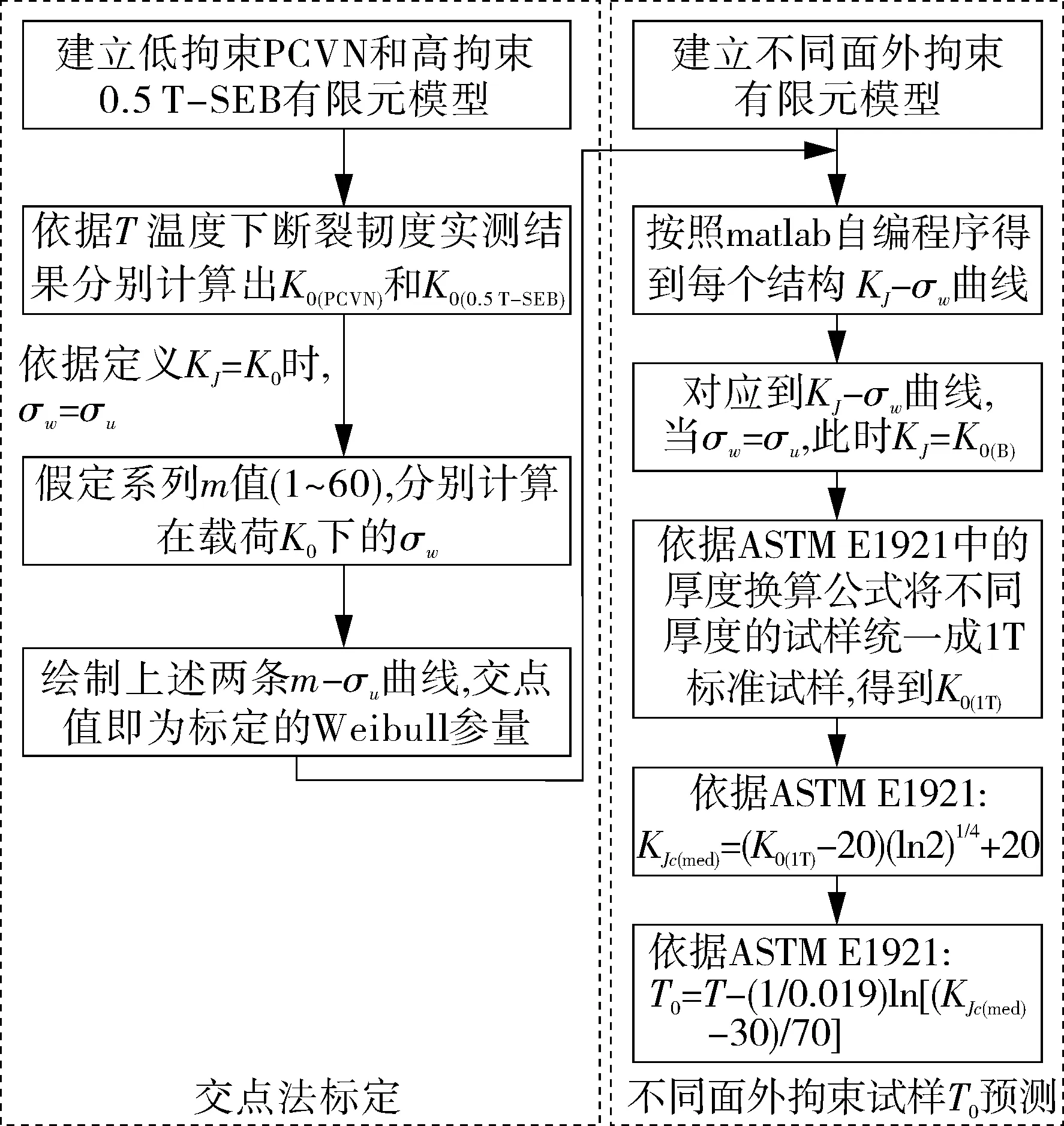
图5 Beremin预测不同面外拘束结构主曲线参考温度流程
分别将0.5T-SEB和PCVN试样的断裂韧度累积失效概率的试验值和基于局部法的预测值绘制于图6中,可以看出,试验和预测的结果基本吻合,尤其是对失效概率63.2%以下的试验数据预测最好,这是由于两参数局部法模型前提假定所致,笔者后期会在这一部分进一步修正。由此可见标定的Weibull参量正确,并且Beremin模型较好地反映出了由于拘束的变化引起的表观韧度变化。

图6 0.5T-SEB与PCVN断裂韧度累积失效概率Pf试验值和预测值比较曲线
韧性换算模型(TSM)是由Ruggieri等[20]于1996年首次提出的,其大致思想是,对某一特定材料,当Weibull应力相等时,不同结构的失效概率是相等的,尽管不同结构由于拘束效应KJ是不同的。基于该思想,可以利用等Weibull应力原理,将任意结构的断裂韧度换算成其他结构的断裂韧度。从第1.2节的结果可看出,ASTM E1921中对于拘束问题仅凭无量纲变形程度Mlimit不能有效地解决。PCVN和0.5T-SEB与标准1T试样相比T0相差50 ℃之多。下面将通过Beremin模型和TSM换算思想解决低拘束试样T0的估算问题,并和试验值相比较,以验证图5中方法的可行性。依据图5中的流程,可以将每一个低拘束的KJc换算到1T标准试样的KJc。图7为PCVN和0.5T-SEB试样韧性换算示意图。
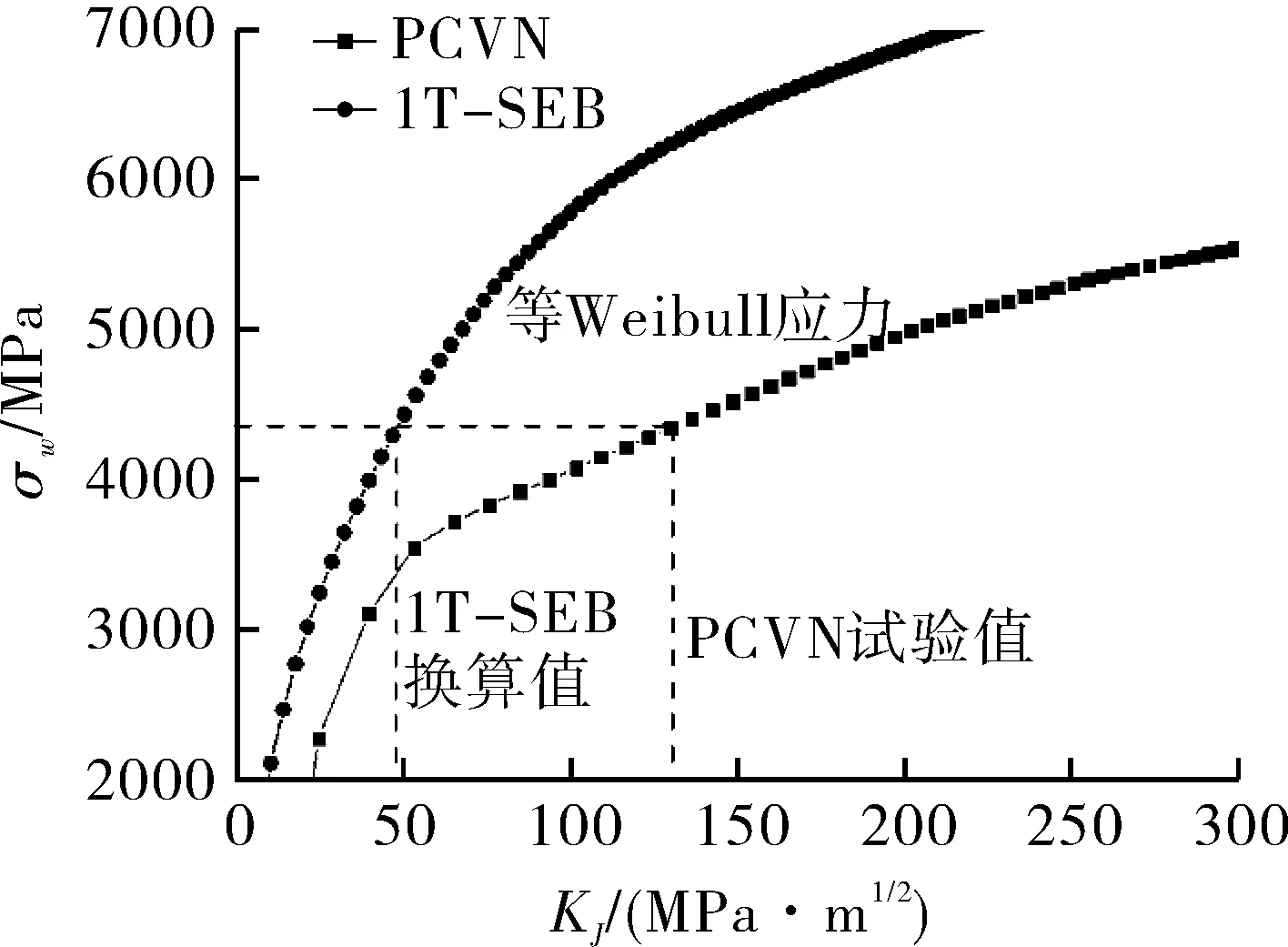
(a)PCVN与1T-SEB
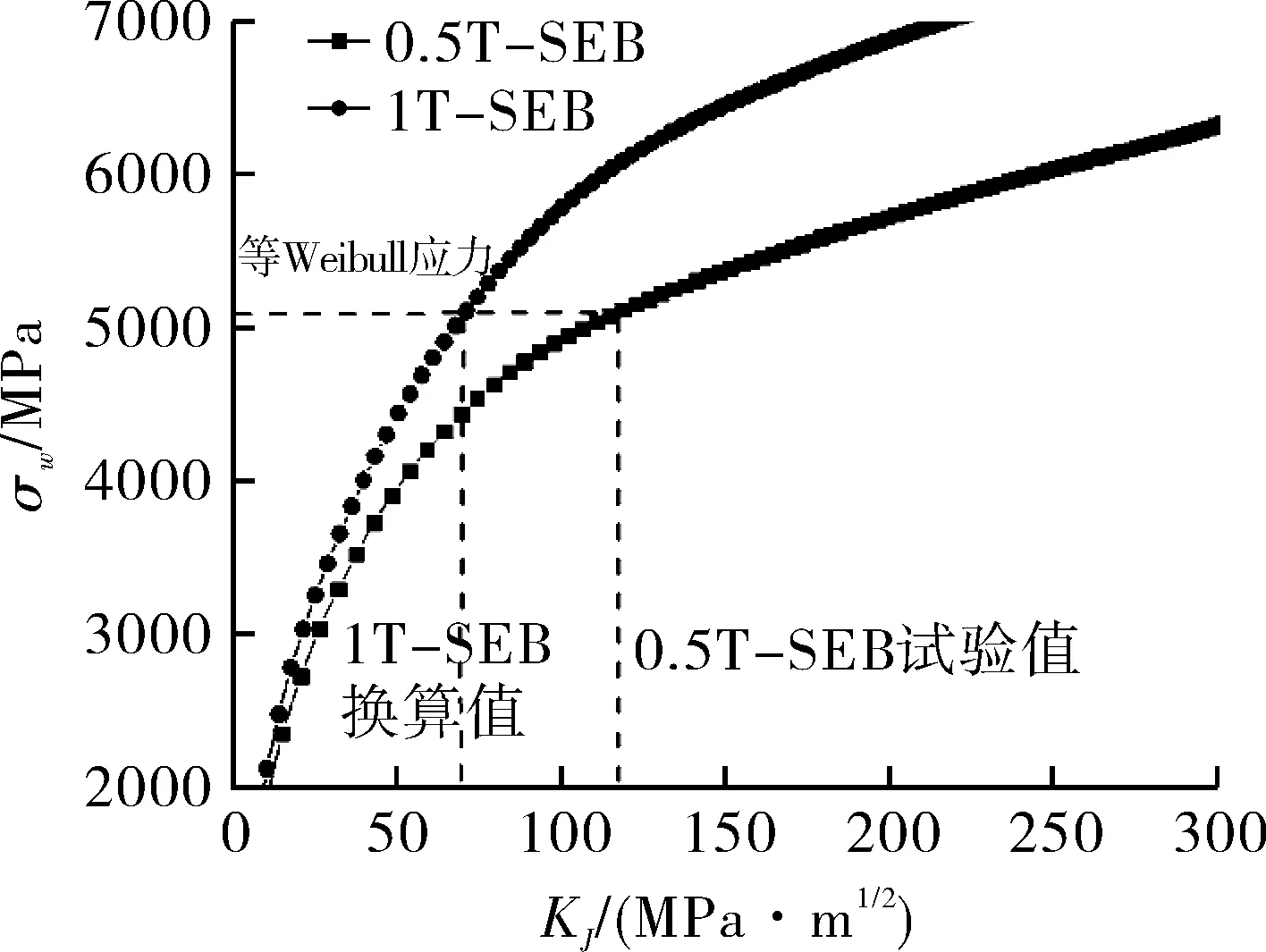
(b)0.5T-SEB与1T-SEB
将试验值换算到1T标准试样的断裂韧度值后,通过式(2)的迭代关系可得到换算后的T0值,见表3。可以看出,换算后的PCVN的T0值大幅度提高到-64.1 ℃,这和1T三点弯曲试验值相差仅1 ℃。0.5T-SEB换算后也有同样的效果。可见Beremin模型和韧性换算方法可以有效地解决拘束修正问题。在实际应用中,尽管标准中允许使用PCVN和0.5T-SEB试样来估计材料的参考温度,不同厚度的断裂韧度也有换算公式,显然这些对Q345R低应变硬化钢的的拘束修正是不合理的。低应变硬化低拘束的试样会过高估计材料转变区间的韧性,在实际安全评价和安全设计中造成严重的安全隐患。
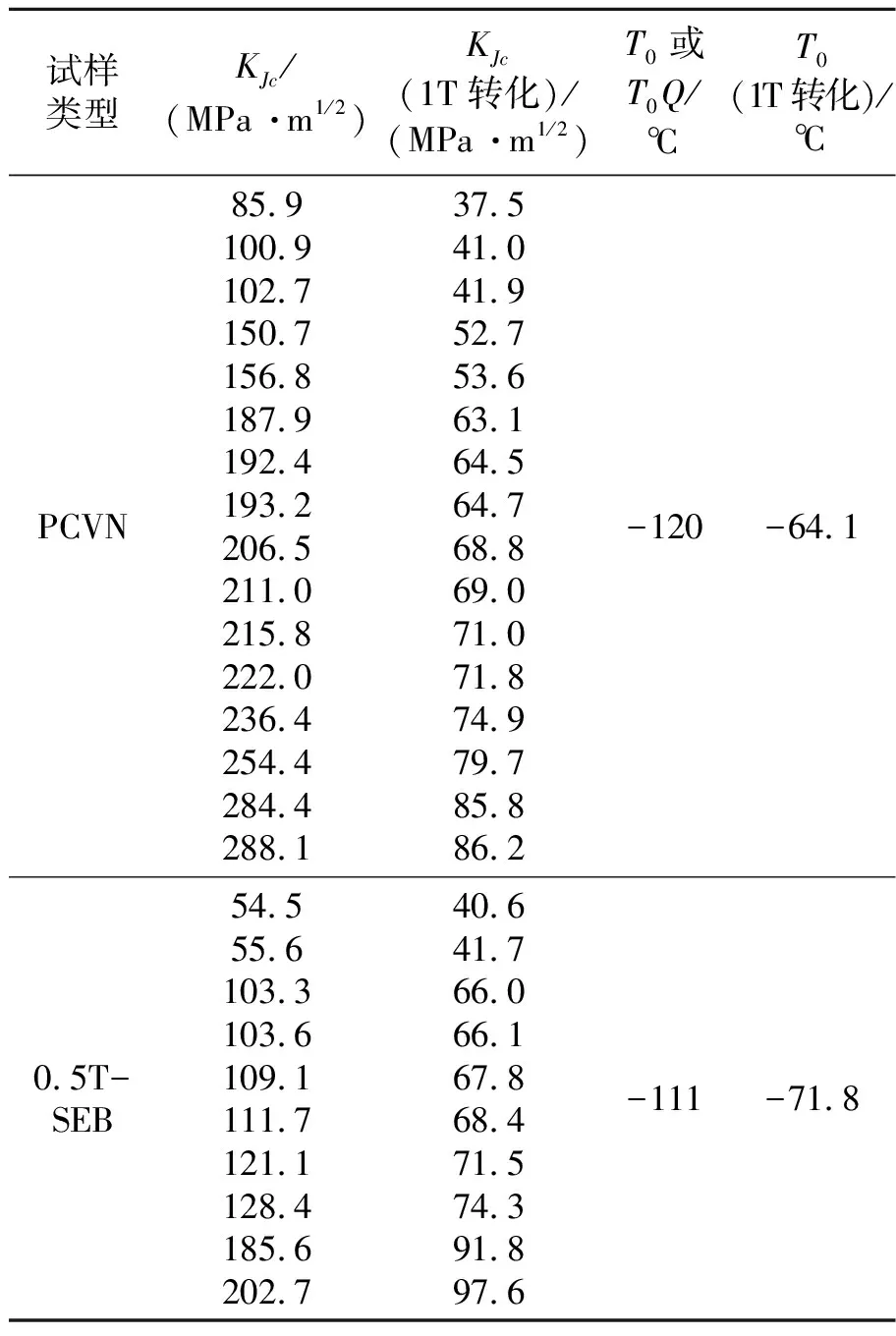
表3 PCVN和0.5T-SEB换算结果
3 面外拘束效应对主曲线法参考温度T0的影响与分析
为了研究面外拘束效应对低温断裂的影响,建立了不同厚度的三点弯曲有限元模型。建模过程同第2.2节,仅厚度发生了变化,试样的面内尺寸与0.5T标准三点弯曲一致,三点弯曲试样支辊跨距S始终等于宽度W的4倍,a/W=0.5,W=25.4 mm。厚度B分别取2.54,7.62,12.70,17.78,20.32,25.40,50.80 mm。
基于图5提出的方法,首先得到不同厚度试样σw-KJ关系,见图8。可以看出,随着外部载荷的增加,Weibull应力首先呈现线性变化,然后是非线性的变化,在比较大的载荷下,曲线之间呈现分离状态,较厚的试样位于左上方、而较薄的位于右上方。在等Weibull应力的条件下,也即相同的累积失效概率下,不同试样的KJ不同,且厚度越小的试样KJ越大,这是由于在断裂前产生过大的塑性流动是一种拘束较低的状态。当厚度小于12.70 mm时,2.54 mm和7.62 mm两个试样的曲线严重偏离,这是因为过薄的试样产生了拘束的缺失。进一步依据图5中的方法,得到了不同厚度试样下的参考温度T0,并通过Boltzmann函数很好地拟合了Q345R三点弯曲试样厚度和参考温度T0的关系,如图9所示,其中Q345R参考温度和试样厚度的拟合方程如下:
(4)
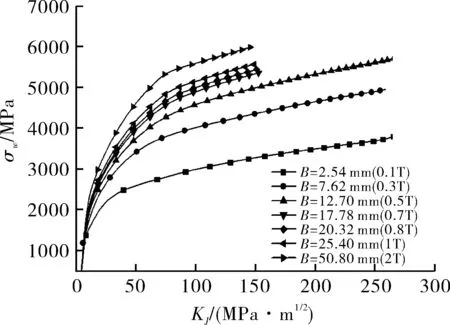
图8 不同面外拘束试样外载荷和Weibull应力之间的关系

图9 不同面外拘束试样厚度和参考温度T0之间的关系
从图9可以看出,随着厚度的减小参考温度值越低,当厚度大于25.4 mm之后,参考温度的变化幅度不大且出现了一个平台。实质上,这是因为试样的拘束接近了平面应变状态,可以估计平面应变状态下这个炉批次Q345R试样的参考温度约为-60 ℃。
图10示出失效概率为63.2%时,对应载荷下不同厚度试样裂纹尖端塑性区尺寸,其中等效塑性应变为0.03。可以看出,厚度越小、塑性区的尺寸就越大,这说明在达到相同失效概率的载荷时,更薄的试样经历了更大的塑性变形,意味着低拘束的情况。Mostafavi等[21]提出了用试样断裂时塑性区面积与平面应变情况下塑性区面积的比值作为一个统一的拘束参数,其研究表明不管是面外拘束还是面内拘束,对试样断裂时塑性区面积的影响是统一的,说明这里用塑性区面积来定性比较拘束的大小是合适的。那么当试样的面外尺寸较小时,若试验材料又为低应变硬化材料,可以推测根据标准测得的参考温度T0结果会严重偏离平面应变或标准试样的测试结果。该结论与ASTM E1921中1.6条款是一致的,拘束程度的降低会造成参考温度T0的降低,这种现象对低应变硬化材料更为明显。因而在实际的结构完整评价中需要纳入拘束效应,才能保证设备安全可靠地运行。


图10 累积失效概率为63.2%、等值线为0.03时的PEEQ云图
4 结论
本文通过三种拘束配置的Q345R钢的断裂韧度数据,通过交点法标定了局部法参量(m=8.2,σu=5 232 MPa)。依据局部法参量的尺寸和载荷无关性,基于韧性换算思想和试验数据校核了局部法参量的正确性,并提出了预测不同面外拘束情况下三点弯曲试样参考温度T0的方法,研究了面外拘束对转变区间参考温度T0的影响,得到了Q345R钢的参考温度和厚度之间的关系,随着厚度的增加,当厚度约超过25.4 mm后会出现一个上平台,-60 ℃为平面应变条件下的参考温度;当厚度低于这个值时会产生严重的拘束缺失现象,参考温度低至-140 ℃。经过分析,这种现象对于低硬化材料更加明显。

