低温绝热气瓶绝热性能检测时间优化分析
侯冀川,蔡延彬,谢柳辉,朱华强,魏国盟,张剑飞
(1.广东省特种设备检测研究院 东莞检测院,广东东莞 523000; 2.西安交通大学 能源与动力工程学院 热流科学与工程教育部重点实验室,西安 710049)
0 引言
低温气瓶主要用于储存低温液态工质,目前广泛应用于不同领域,如:储存液体火箭发动机燃料、作为氢燃料车储罐以及应用于低温生物学和低温电子学等[1-2]。低温气瓶良好的绝热性能是实现储存低温液态工质的重要保证。
低温气瓶一般由内胆和外壳组成[3]。低温气瓶的漏热途径根据不同绝热方式而有所不同,以高真空多层绝热为例,其漏热途径主要有真空夹层之间的辐射传热、残余气体导热以及支撑构件导热等三部分[4]。这些漏热情况导致储存在低温气瓶内的液体蒸发而压力升高,直至逸出造成浪费;同时,如果泄压阀发生损坏,甚至会引起重大事故[5]。在某些野蛮作业场所不合格产品,更易引发事故[6]。因此低温气瓶的安全必须得到保障。
蒸发率是低温绝热气瓶在自身材料结构和外部条件影响下的绝热性能的一个重要体现。一般来说低温绝热气瓶蒸发率的外部影响因素主要有:环境温度、环境压力、充满率等[7-11]。我国标准[12]规定,低温绝热气瓶正式检测时间必须不少于48 h,而国际标准[13]也规定了这一检测时间不少于24 h。缩短检测时间将对低温绝热气瓶的工业检测具有重要意义。
针对低温气瓶的研究多数集中在绝热性能提高方面,国际上有不少学者[14-16]研究了多层绝热方式的优化方法,并发展出了对应的传热计算模型,被广泛应用的主要有两种:Layer-by-Layer模型和Modified Lockheed模型[17]。这些模型主要用于低温气瓶的设计计算,且计算时需要给定部分参数,如计算构件导热时,需要知道对应构件的温度[18],而不同结构的支撑构件漏热也不尽相同[19],因此以上模型并不适用于作为检测绝热性能时的优化方法。
本文在一维传热模型的基础上,提出一种用于低温绝热气瓶蒸发量快速检测模型。该方法与实际检测过程相结合,利用短时间的检测数据作为样本来预测剩余时间内的蒸发量。
1 实验台搭建及试验流程
试验在恒温箱中进行,恒温箱内部温湿度可调,压力与环境压力一致。恒温箱尺寸为2.5 m×2.3 m×3.2 m,试验过程中可同时放置4只气瓶。恒温箱外观如图1所示。
开始检测前,向待检测气瓶充液,所用工质为液氮,将气瓶充液至额定充满率,静置48 h后,将气瓶移入恒温箱内部,开始蒸发率检测工作。检测时,恒温箱内分别设置不同的温度,以寻找最合适的恒温环境。待一个工况完成后,将气瓶重新充液至额定充满率,再次静置,静置完成后移入恒温箱开始试验。每一个工况均是如此操作,以保证同一只气瓶的初始状态一致。

(a)恒温箱外部

(b)恒温箱内部
试验过程中主要测量的参数有:环境温度、环境压力、气体蒸发流量以及流量计入口气体温度。采集数据所用的相应设备参数见表1。

表1 设备参数
试验中所使用的低温绝热气瓶规格参数及结构分别见表2和图2。

表2 3种低温绝热气瓶的尺寸参数
(a)立式

(b)卧式
2 检测时间优化方法设计
2.1 一维传热模型
将低温绝热气瓶内部的漏热量分为两部分:气相漏热和液相漏热。总漏热量计算公式如下:
Q=qmr
(1)
式中Q——总漏热量,W;
qm——气体蒸发质量流量,kg/s;
r——液氮的汽化潜热,kJ/kg。
气体蒸发质量流量可由体积流量计读数计算得出,试验时已经将体积流量计读数自动换算成标准状态下的参数。
前文已经提到,低温绝热气瓶的漏热途径根据实际的绝热方式而有所不同。很多文献都已经对其计算方法进行了详细介绍,比较著名的有Layer-by-Layer模型和Modified Lockheed模型。但是这种模型计算公式相对复杂,多用于设计计算,且需要测量的参数较多,不适合用于作为检测时的计算模型。本文采用经典的传热学公式进行计算。
Q=Qg+Ql
(2)
式中Qg——气相漏热量,W;
Ql——液相漏热量,W。
考虑到气相空间存在温度分层现象,所以气相空间漏热计算相对不易,本文采用气液相漏热比例系数GLA[20]通过液相计算气相漏热量Qg以及总漏热量Q。该比例系数定义为:
(3)
式中Nu——流体与内壁面对流换热的努赛尔数;
λ——流体导热系数W/(m·K);
ΔT——流体与内壁面的温差,K;
L——流体定性尺寸,m;
A——流体与内壁面接触面积,m2;
下标l,g——液相和气相。
由此,总漏热量方程可改写为:
Q=klAl(Tamb-Ts)GLA
(4)
式中kl——液相漏热总传热系数,W/(m2·K);
Al——液相与气瓶内壁接触面积,m2;
Tamb——外界环境温度,K;
Ts——环境压力下的液氮饱和温度,K,可由NIST数据库根据环境压力查出。
气瓶检测的主要目的在于检测其绝热性能是否合格,式(4)中的总传热系数kl正好反映了低温气瓶的绝热特性。本文的基本思路是利用试验数据获取这一传热系数,并认为在短时间内该传热系数保持不变,从而依据这一参数获取低温气瓶在外界环境变化时的蒸发流量,实现利用较少时间完成检测的目的。
在获取传热系数后,可反向计算漏热量,从而实现蒸发质量和蒸发率的计算。由传热系数计算蒸发流量的过程采用以下公式:
(5)
式中kl′——实测时间内平均传热系数,W/(m2·K)。
2.2 优化方法设计
为了实现利用较少时间完成低温绝热气瓶蒸发率检测的目标,本文结合传热模型分析建立的计算流程及验证方法如图3所示。

图3 优化方法流程图及验证方法
结合流程图,具体实施方法如下:
(1)按照标准充装并静置48 h;
(2)静置完毕后开始记录数据,持续24 h;
(3)分别选取前6 h,12 h以及18 h的数据作为样本,由式(1),(3),(4)分别计算对应的总漏热量、气液相漏热比例系数以及液相漏热总传热系数并对传热系数取平均值;
(4)利用式(5)计算剩余时间段内的瞬时蒸发质量流量;
(5)计算累计24 h内的总蒸发质量。
首先按测试标准规定的时间完成了蒸发量检测,并记录相关参数。同时利用文中提出的方法进行蒸发率的预测,通过试验测量值与计算值的对比,以验证模型的有效性。
3 结果分析与讨论
3.1 恒温箱温度的影响
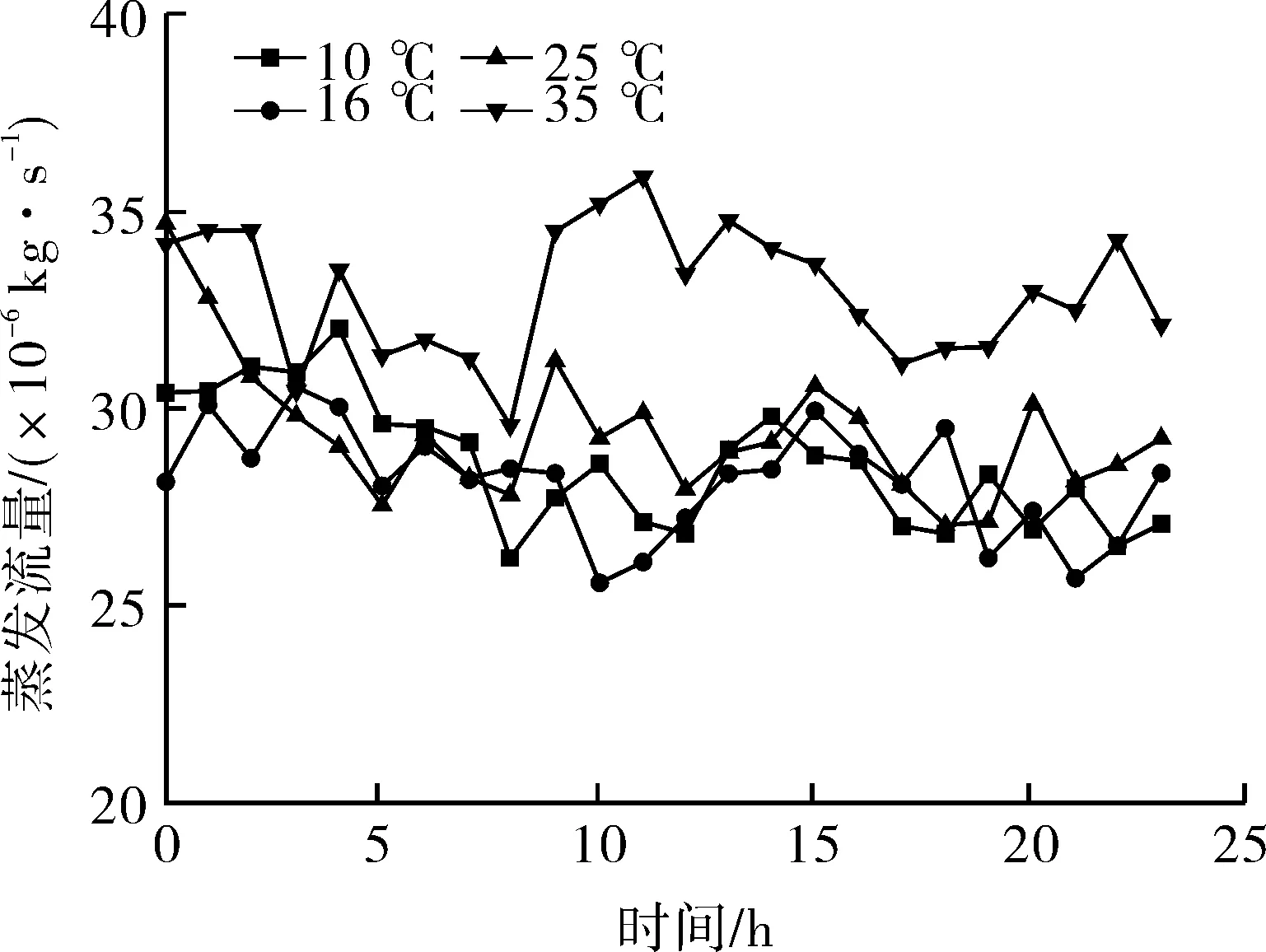
本文试验在恒温箱中进行,一共设置了5组温度工况,分别为10,16,25,30,35 ℃。由图4可以看出,温度越高,气瓶内外的温度差越大,传热动力越强,蒸发流量随之增大。本文选取的5组温度分别模拟了测试地点的4个季节的温度变化。由于外界压力的变化,即使将气瓶放于恒温箱中检测,瞬时蒸发流量仍处于波动状态。

(a)175 L气瓶
(b)195 L气瓶

(c)330 L气瓶
3.2 优化检测方法的验证
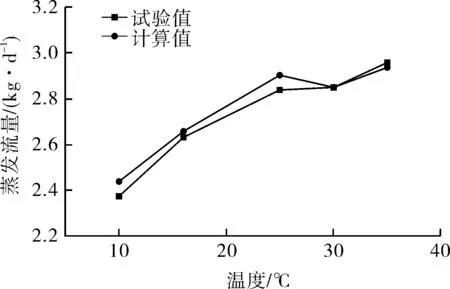
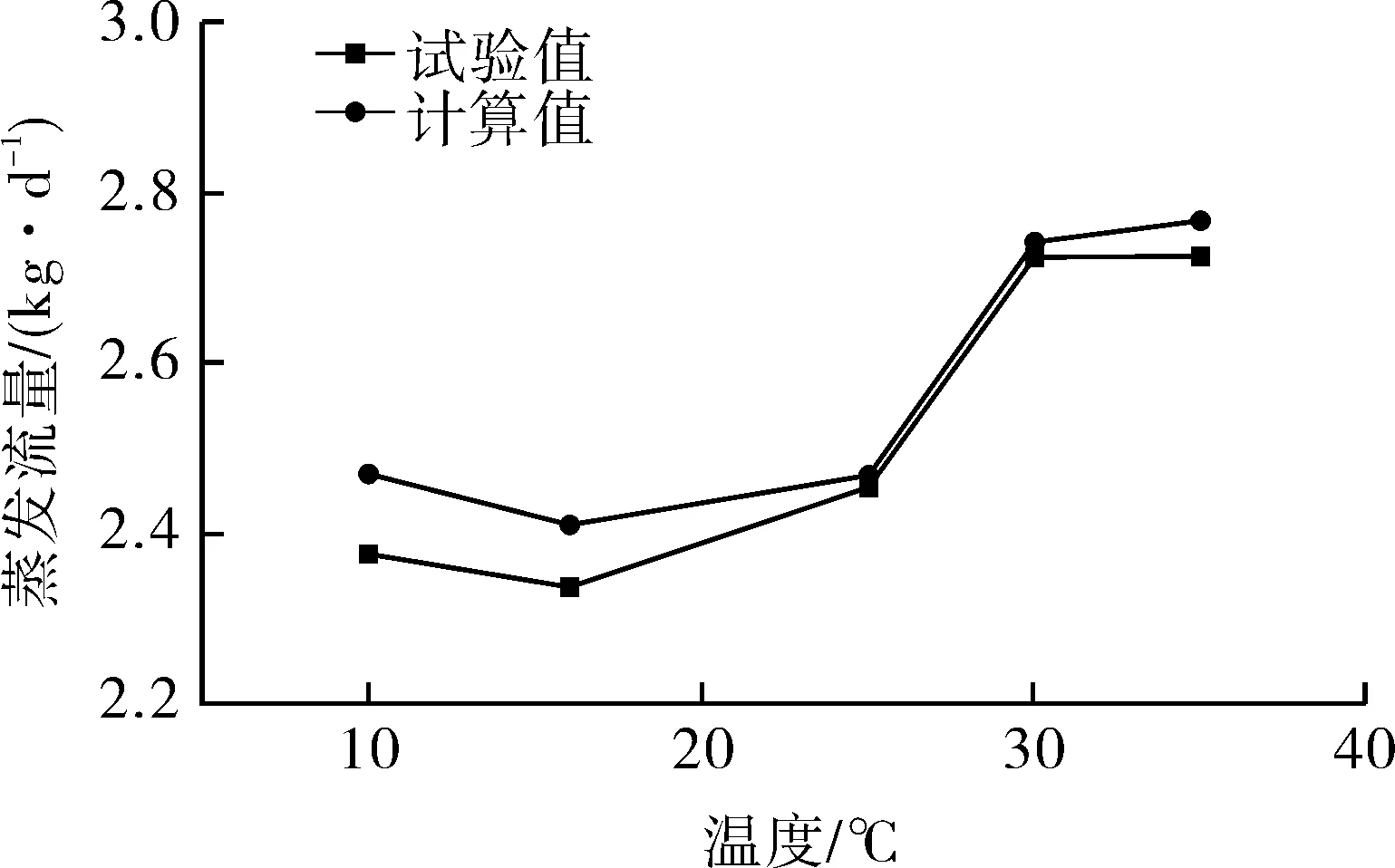
根据第2.2节,选取一定时间内的试验数据作为样本,用于预测剩余时间的蒸发流量。图5,6示出了预测的结果。其中,图5中选取了前6 h的数据作为样本,剩余18 h的数据由第2.2节方法计算而得。用于考核模型的参数为24 h内累计蒸发质量。计算结果表明,对于3种规格的气瓶,利用本文方法计算出的24 h内累计流量略高于试验测量的累计流量,且误差均在5%以下。
(a)175 L气瓶
(b)195 L气瓶

(c)330 L气瓶
(a)175 L气瓶

(b)195 L气瓶

(c)330 L气瓶
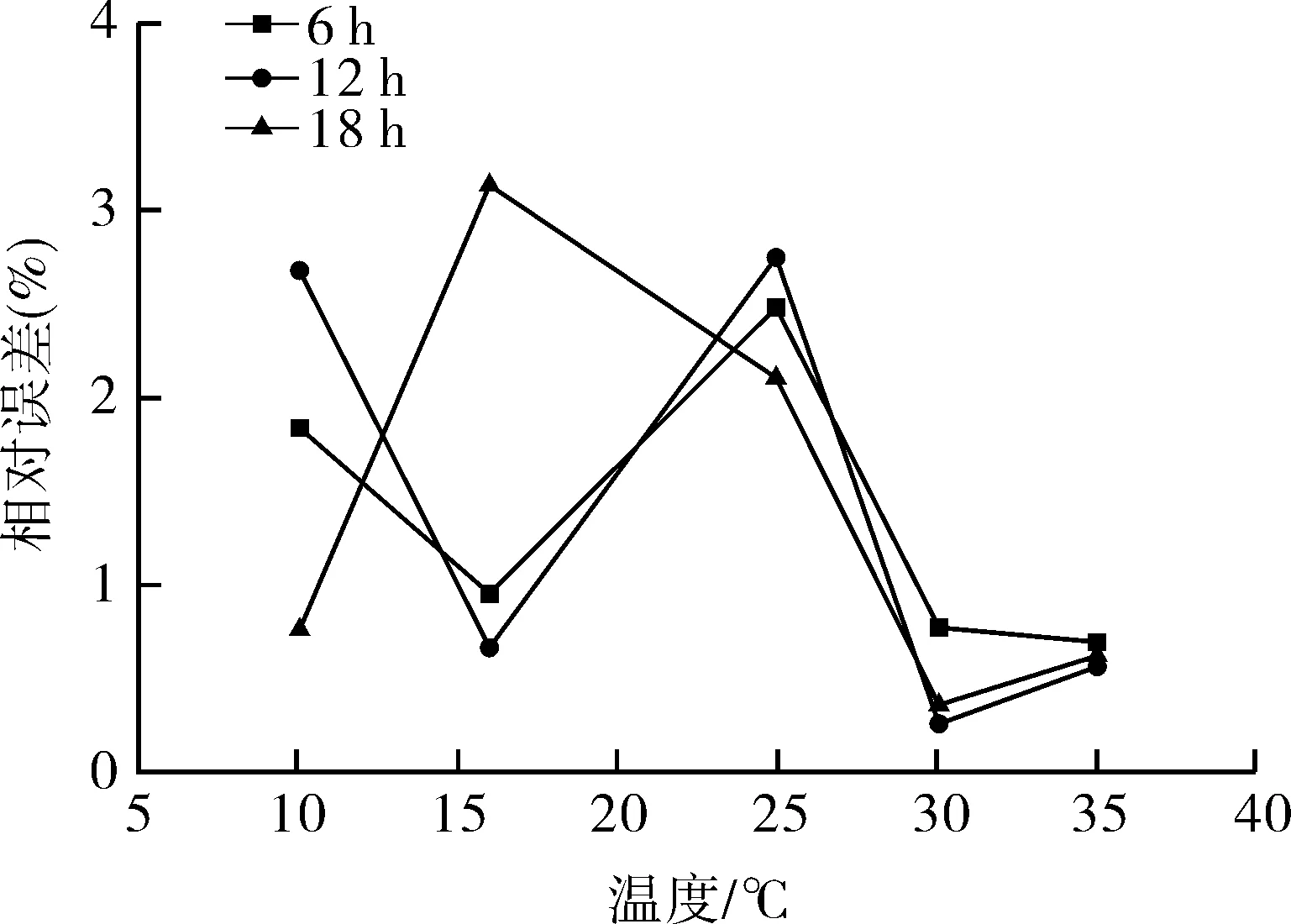
为了确定最佳实测时间,本文分别选取了6,12,18 h的试验数据作为样本,并对计算结果进行比对,其相对误差见图6。当选取的样本时间变化时,累计流量误差随之变化。由于绝热气瓶瞬时蒸发流量受多种因素影响,因此选取不同时间长度的数据样本时,计算值与实际值之间的相对误差变化并无明显规律可言,但相对误差均在5%以内,因此选取6 h的试验数据样本,即可准确预测蒸发量的变化。但在恒温箱温度选取方面,大致呈现出了温度越高时、预测精度随之上升的规律。
4 结论
本文采用半试验半预测的方法,结合低温绝热气瓶一维传热模型,提出了一种针对检测时间的优化方法。该方法的主要思想是利用检测过程中的一部分数据作为样本,认为气瓶的绝热性能在一定时间内基本保持不变,从而建立了样本数据与待预测时间段内预测值之间的联系,并得到了以下结论。
(1)恒温箱温度对低温绝热气瓶累计质量的计算值和试验值之间的相对误差有一定影响,根据试验发现,温度升高时,相对误差有变小的趋势。
(2)采用气瓶在24 h内的累计蒸发质量作为考核指标,发现计算值与实际值相对误差能稳定在5%以下,因为可认为本文提出的方法有效,并在低温绝热气瓶性能检测方面具有一定的应用价值。

