低温恒温箱的非稳态数值模拟及验证

杜子峥 谢 晶 朱进林

（1.上海海洋大学食品学院，上海 201306；2.上海水产品加工与贮藏工程技术研究中心，上海 201306）

低温恒温箱已广泛应用到医疗、科研、军事等多个领域，其在食品贮藏研究中使用更是广泛，试验样品往往需要在恒定温度下进行贮藏，低温恒温箱内部不合理温度分布将导致试验精度下降，从而影响试验结果，因此有必要对低温恒温箱内部流场和温度分布进行研究。

计算流体力学（computational fluid dynamics，CFD）相对于高成本试验，因其低花费、高可靠性，已经广泛应用在航空航天、气象、水文等多个领域，其在改进现有工艺、设计和开发新产品上有明显的优势，而且可作为试验数据的补充和参照，研究人员可以修改多个参数，获得不同试验结果，这往往是单一试验所无法完成的。目前，计算流体力学在冷库和冰箱流场分布模拟中应用较多，Gonalves等［1，2］、Belleghem等［3］和Jaramillo等［4］对冷库风幕进行数值模拟，在不同风幕吹风角度、速度下确定了冷库风幕最优运行参数。Chourasia等［5］和Delele等［6］对有货物贮藏情况冷库内部的温度和气流组织分布进行数值模拟，确定了最优货物摆放方式和堆垛尺寸以改善内部温度分布情况。Amara等［7］对家用冰箱进行数值模拟并利用粒子图像测速技术（PIV）对冰箱内部气流流速分布进行试验检测，模拟值和测量值具有良好一致性。António等［8］以冷藏柜为研究对象，分别采用CFD技术和ANN模型对冷藏柜内部温度分布进行模拟，发现采用ANN预测温度分布绝对误差（0.8K）小于CFD预测误差（1K），ANN模型预测温度分布更准确。Kumluta等［9］在家用冰箱的数值模拟中也采用了ANN（人工神经网络）模型，试验最大相对误差仅有2.32%，验证了ANN模型预测冰箱温度分布的准确性。张敏等［10］对两种不同送风形式（上出风型和下出风型）低温恒温箱气流组织进行模拟和实验验证，提出上出风型恒温箱降温效果优于下出风型恒温箱，但下出风型恒温箱气流分布更均匀。Guo-Liang Ding等［11］利用Star-CD软件对采用自然对流形式的冰箱进行了CFD模拟，指出货架与冰箱前后壁的间距是影响其内部温度分布的关键因素，缩小间距有助于冰箱内部温度均匀分布，最后设计了一种强制通风装置改善冰箱内部气流组织分布。目前，有关低温恒温箱降温过程非稳态模拟文献鲜见，而为提高低温恒温箱控温精度，有必要对其内部降温过程和气流组织分布进行研究，提出改进低温恒温箱设计的建议，从而提高其温度分布的均匀性。

1 模型的建立

1.1 物理模型

本试验研究对象是一个尺寸为55cm长×64cm宽×124cm高，采用强制通风形式的低温恒温箱，其圆形出风口位于低温恒温箱壁面中上部，距离顶壁15cm，直径为1 0cm；矩形回风口位于出风口同侧底部，尺寸为9cm宽×6.5cm高，低温恒温箱隔热材料为0.06m厚聚氨酯夹芯板，其热导率为0.022W/（m·K），模型结构见图1。

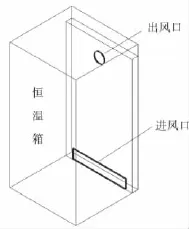
图1 低温恒温箱结构示意图Figure 1 Mathematical model of the cryostat

为简化计算，本次模拟做了以下几点假设：

（1）低温恒温箱内气体为不可压缩理想气体且符合Boussinesq假设；

（2）不考虑恒温箱箱门处的冷风渗透率；

（3）忽略恒温箱内部的辐射传热；

（4）不考虑恒温箱内部降温过程中因相对湿度变化导致系统吸收的潜热；

（5）壁面具有相同的热导率且外界温度为恒定测量值。

1.2 网格划分及边界条件设定

首先用GAMBIT软件对计算域进行非结构网格划分，非结构网格对几何模型的适应性好，多用于对复杂区域进行网格划分。计算域网格尺寸采用1.5cm，共生成网格数量为152 928个。

低温恒温箱出风口平均流速经过实际测量为0.6m/s，经计算雷诺数Re＝24 500为湍流，因此采用标准k－ε模型进行求解。近壁区域需要使用壁面函数进行处理，大多数高雷诺数情况可使用标准或非平衡的壁面函数（Re＞106），本次模拟使用增强壁面处理，因其对复杂流动尤其是低雷诺数流动很适合。

表1 k－ε方程中的系数Table 1 Coefficients in k－εmodel

1.3 计算条件

谢晶等［12］利用PISO算法在对小型冷库开关门过程进行非稳态模拟，提出PISO算法适用于瞬态过程；缪晨等［13］同样利用PISO算法对有空气幕冷库开关门过程温度和流场分布进行预测；杨磊等［14］在冷藏库预冷降温过程非稳态模拟中同样使用PISO算法，PISO算法对于瞬态问题收敛效率较高，因此本次模拟采用PISO算法，微分离散格式选项中，压力空间离散因引入Boussinesq假设采用PRESTO格式，其余项采用二阶迎风格式以提高计算精度。

2 出风口温度函数

降温过程出风口温度随着时间增加逐渐降低，其过程呈现非稳态变化，若在Fluent中将出风温度设定为一恒定值，模拟结果与测量结果之间将存在极大误差，从而影响整个试验结论。因此有必要对低温恒温箱出风口温度进行测量，绘制出风温度变化曲线，选择准确的函数对温度变化曲线进行拟合，利用UDF模块将拟合函数编入Fluent中来定义出风温度。

2.1 测量方法

为验证模拟精度和实现对出风口温度准确测量，需对恒温箱空箱降温过程进行测试，试验共在恒温箱内部布置16个T型热电偶（见图2），利用Fluke-NetDAQ32多点测温仪（美国Fluke公司）对数据进行采集，T型热电偶精度为±0.5℃，热点偶主要布置在恒温箱6个壁面中心，回风口以及出风口。考虑到蒸发器的安放位置，测试将4个T型热电偶以十字形式布置在恒温箱圆形出风口上，每个T型热电偶间距为5cm。将恒温箱贮藏温度设定为－4℃，启动低温恒温箱同时开始记录温度数据，每隔20s对各测试点温度数据进行采集，直到监测点温度开始出现周期性波动后停止测量，对出风口4个监测点温度取平均值并绘制温度变化曲线（见图3）。

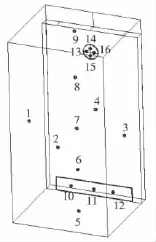
图2 恒温箱内部测温点布置示意图Figure 2 Arrangement of temperature measuring

2.2 拟合函数

出风温度变化曲线有多种函数可对其进行拟合。杨磊等［14］在对冷库预冷降温过程数值模拟和试验研究中，使用二次多项式对出风温度曲线进行线性拟合；杨昭等［15］利用指数函数对保鲜库实测送风温度进行线性回归。为实现出风温度变化的准确预测，本试验建立了二维恒温箱模型，使用线性回归方程（三次多项式、五次多项式、指数函数）对出风温度测量值进行拟合，拟合优度分别为0.992 69，0.998 00和0.991 64，拟合优度是指回归直线对观测值的拟合程度，拟合优度越接近1，说明回归直线对观测值拟合程度越好。从拟合优度指标判断，五次项拟合函数对出风温度拟合度最高。

图4是将3种不同拟合函数编入Fluent中并对降温过程进行模拟得到的出风口温度线性回归曲线。当降温过程达到第26分钟（第1 600秒）时，出风口温度开始周期性变化，由于出风温度开始发生周期变化时，库内温度已经达到相对稳定，因此波动过程不计入拟合过程，只对降温过程曲线进行拟合。

图5是基于二维CFD技术预测不同出风温度函数下的恒温箱平均降温曲线，3种出风温度函数温度模拟值均低于实际测量值，这可能是由于二维模拟无法预测水平方向上的传热，并不能够准确反映真实的降温过程。三次多项式、五次多项式和指数函数在平均温度预测上最大误差分别仅为1.12%，1.13%，1.26%，三者较接近，因而仅从这一指标无法判断这3个函数的优劣。模拟结果显示在降温前40s，五次项出风温度函数预测的平均温度有一个明显升温过程，在第20秒温度上升最高到29.5℃，这可能导致错误预测降温前期恒温箱内部温度分布，延长整个模拟降温的时间。其他两种函数均能正确反映恒温箱降温过程，与测量值误差分别仅为0.1℃和0.2℃。三次项函数在降温后期过度预测了恒温箱内部的降温效果，在第1 600秒模拟降温值达到－6℃，而恒温箱内部平均温度测量值为－4.1℃，指数函数在整个恒温箱降温过程对内部温降预测准确，且最终模拟值与测量值误差仅为0.08℃，远远低于三次项函数1.95℃和五次项函数的1.35℃，因此本次模拟出风口温度选择指数拟合函数，指数方程为：

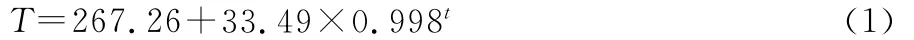
式中：

T——出风口的平均温度，K；

t——降温时间，s。

该控制方程使用UDF编入Fluent中（udf＿temperature.c），对三维恒温箱降温过程进行预测，3种出风拟合函数见表2。

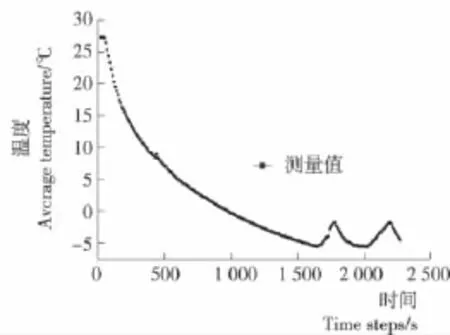
图3 恒温箱平均出风温度Figure 3 Curve of cryostat average temperature

图4 不同函数形式对出风温度拟合曲线Figure 4 Fit curves of outlet temperature utilizing different function

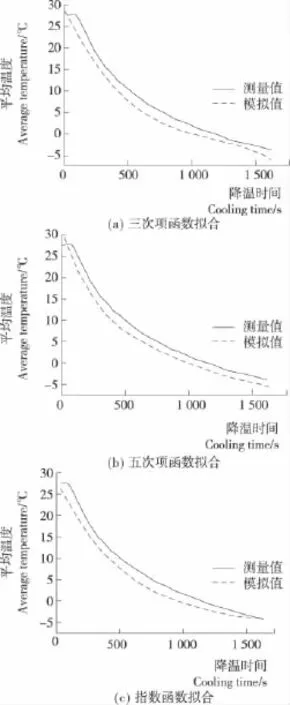
图5 不同拟合函数下箱内平均温度的模拟值与测量值对比Figure 5 The comparison between simulation temperature and experiment temperature by different functions

表2 3种函数对出风温度的拟合方程Table 2 Fitting equation of outlet temperature with three kinds of function

3 非稳态模拟结果与分析

3.1 温度分布

图6为三维恒温箱降温过程测量值和模拟值降温曲线，模拟选取指数函数对出风口温度进行线性回归后，实际测量值和模拟值之间的误差进一步缩小，最大误差仅为0.82%，低于二维恒温箱模型最大误差1.26%，说明三维CFD模拟技术与二维相比更具有可靠性，模拟的整个精度得到显著提高，测点拟合温度和测量温度对比见图7。

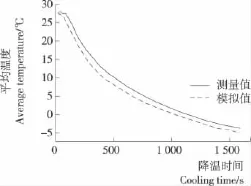
图6 三维恒温箱平均温度模拟值和测量值对比Figure 6 The comparison between simulation temperature and experiment temperature

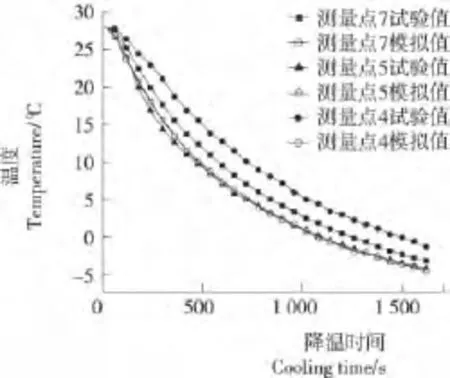
图7 恒温箱测点温度试验值与模拟值的比较Figure 7 Comparison of predicted temperatures with experimental temperatures in cryostat

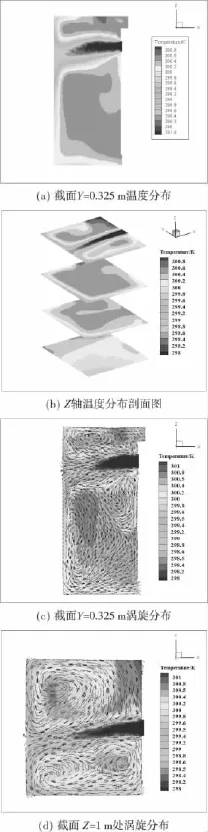
图8 恒温箱降温1min时温度场和涡旋场分布示意图Figure 8 Temperature fields and vorticity distribution of cryostat after running 1minute

图8（a）和图8（b）显示恒温箱降温1min时温度分布剖面图，中心主流沿射流方向温度逐渐降低，到达壁面发生弯折并贴近壁面流动，造成近壁面处降温迅速，中心主流由远离出风口一侧壁面逐渐向内部进行对流换热，恒温箱内回风口处形成一个回风主流区域，回风主流两侧有两个对称的温度较高区域，热气流在密度差作用下向恒温箱内部和上部区域扩散，使得这两个区域降温速率较缓慢，荆有印等［16］在冷库CFD研究中指出涡旋区域往往是低温贮藏货物最差区域，图8（c）为降温1min时Y＝0.325m的涡旋分布截面图，在恒温箱顶部风机远端形成一个涡流区，在恒温箱中心区域同样发现两个涡旋区域，而涡旋中心也是降温过程中温度最高区域；图8（d）显示在中心主流两侧也形成多个涡旋区域，上部形成的较大涡旋迫使扩散主流发生偏移，而涡旋的产生往往会伴随机械能损耗，图8（c）和图8（d）在近壁区域形成多个涡旋，导致气流动能减少，从而降低了恒温箱内部气流流速，影响内部降温过程。图9显示随着降温过程继续，恒温箱底部温度均匀度得到改善，但中心和顶部区域仍是整个结构温度分布最高区域，在恒温箱顶端和中心左侧仍发现存在两个涡旋，涡旋处温度逐渐降低，这可能是由于紊流能量级联过程［17］，时均紊流向流场最大尺度涡旋提供其运动所需能量，随过程发展向能量较小尺度涡旋传递，最终将机械能消耗转化成内能，造成大涡处温度降低，涡旋周边温度升高，图9（c）显示恒温箱风口远端近壁处涡旋上移并且涡量增大迫使出风扩散主流向上偏移。图10为26min时恒温箱内部平均温度达到设定值－4℃数值模拟的温度和涡旋分布剖面图，中心和顶端仍是降温最差区域，近壁面左侧两个涡流仍未消失。整个降温过程，恒温箱中心主流两侧及恒温箱中心近壁区域始终存在涡旋，造成气流分布不均匀，影响恒温箱顶部右侧和中心区域降温。

图9 恒温箱降温10min时温度场和涡旋场分布示意图Figure 9 Temperature fields and vorticity distribution of cryostat after running 10minute

图10 恒温箱降温26min时温度场和涡旋场分布示意图Figure 10 Temperature fields and vorticity distribution of cryostat after running 26minute

3.2 速度分布

图11为降温过程Y＝0.325m处XZ轴速度矢量分布剖面图，随着降温过程进行，恒温箱内速度分布得到明显改善，出风主流沿程流速逐渐降低，在末端壁面上下两处形成风速较高区域，恒温箱内部平均风速从降温初期0.09m/s逐渐降低到0.065m/s，内部主要贮藏区域风速始终处在0.05～0.10m/s区间，出风主流远端壁面上部和下部始终存在速度较低区域，这也恰好存在涡旋，流体合理的温度和速度是货品冷却过程至关重要的两个因素，恒温箱内部涡旋的产生不但使温度分布不均匀而且导致涡旋处和恒温箱内部流速降低，影响样品冷却过程，因此有必要对恒温箱进行改进以消除涡旋的产生。

图11 恒温箱截面Y＝0.325速度分布示意图Figure 11 Cross-section of velocity distribution（Y＝0.325）

4 结论与展望

本研究引入Boussinesq假设，采用PISO算法并对出风温度进行修正，模拟了恒温箱内部降温过程，从模拟和试验结果，得到以下结论：

（1）结合前人研究，本试验对3种不同出风温度拟合函数进行讨论，确定指数函数更适合预测恒温箱降温过程，模拟值和试验值最大误差仅为0.82%。

（2）整个降温过程恒温箱顶端和中心区域左侧始终存在两个涡旋区域，其对气流的动能耗散效应导致内部气流速度减慢，影响内部降温过程。

本研究对恒温箱空箱降温过程进行了CFD模拟，未来研究还可以从以下几方面展开：

（1）利用CFD技术对有热源情况下恒温箱降温过程进行数值模拟，对货物在不同呼吸强度、几何形状、摆放方式下温度分布进行研究，寻找最优化方案。

（2）研究开关门过程对恒温箱内部降温及温度分布影响，对采用强制通风形式的恒温箱，选取合适的气流速度及设备抵御开关门过程中外部热质侵入。

3 Belleghem M，Verhaeghe G，T＇Joen C，et al.Heat transfer through vertically downward-blowing single-jet air curtains for cold rooms［J］.Heat Transfer Engineering，2012，33（14）：1 196～1 206.

4 Jaramillo J，Pérez-Segarra C，Oliva A，et al.Analysis of the dynamic behavior of refrigerated spaces using air curtains［J］.Numerical Heat Transfer：Part A – Applications，2009，55（6）：553～573.

5 Chourasia M K，Goswami T K.Simulation of effect of stack dimensions and stacking arrangement on cool-down characteristics of potato in a cold store by computational fluid dynamics［J］.Biosystems Engineering，2007，96（4）：503～515.

6 Delele M A，Schenk A，Tijskens E，et al.Optimization of the humidification of cold stores by pressurized water atomizers based on a multiscale CFD model［J］.Journal of Food Engineering，2009，91（2）：228～239.

7 Ben Amara S，Laguerre O，Charrier-Mojtabi M C，et al.PIV measurement of the flow field in a domestic refrigerator model：Comparison with 3Dsimulations［J］.International Journal of Refrigeration，2008，31（8）：1 328～1 340.

8 António C C，Afonso C F.Air temperature fields inside refrigeration cabins：a comparison of results from CFD and ANN modelling［J］.Applied Thermal Engineering，2011，31（6）：1 244～1 251.

9 Kumluta爧D，Karadeniz Z H，Avci H，et al.Investigation of design parameters of a domestic refrigerator by artificial neural networks and numerical simulations［J］.International Journal of Re-frigeration，2012，35（6）：1 678～1 689.

10 张雷杰，张敏，杨乐，等.两款恒温箱的气流组织模拟与实验验证［J］.安徽农业科学，2009（18）：8 752～8 754，8 764.

11 Ding G L，Qiao H T，Lu Z L.Ways to improve thermal uniformity inside a refrigerator［J］.Applied Thermal Engineering，2004，24（13）：1 827～1 840.

12 谢晶，吴天.小型冷库开关门过程温度场的数值模拟［J］.上海水产大学学报，2006（3）：3 333～3 339.

13 缪晨，谢晶.冷库空气幕流场的非稳态数值模拟及验证［J］.农业工程学报，2013（7）：246～253.

14 杨磊，汪小旵.冷藏库预冷降温过程中温度场的数值模拟与试验研究［J］.西北农林科技大学学报（自然科学版），2008（9）：219～223.

15 杨昭，徐晓丽，李喜宏.保鲜库三维非稳态流场模拟及实验［J］.天津大学学报，2007（2）：157～162.

16 荆有印，王长海，丁桂艳，等.旋转气流及货物对冷库流场影响的研究［J］.冷藏技术，2008（4）：34～37，41.

17 叶飞.非稳态漩涡运动及其产生机理［D］.天津：天津大学，2010.