摆动推进鱼类鱼体波复模态分解及其特性分析

崔 祚, 姜洪州

摆动推进鱼类鱼体波复模态分解及其特性分析

崔 祚1, 姜洪州2

(1. 贵州理工学院 航空航天工程学院, 贵州 贵阳, 550003; 2. 哈尔滨工业大学 机电工程学院, 黑龙江 哈尔滨, 710077)

在自然界中, 大多数鱼类通过身体和尾鳍的复合波动形成独特的鱼体波曲线, 以获得其快速高效的游动性能。文中以鱼体波为研究对象, 采用复模态正交分解(COD)方法来研究鱼体的复合波动模式。从振动模态的角度看, 鱼类的游动是粘弹性鱼体在流体中的强迫振动, 鱼体波对应的是复模态振型。根据COD方法, 将鱼体波分解为纯行波和纯驻波两部分, 并利用复模态振型实部和虚部的相关系数来定义鱼体波的行波系数。通过分析鳗鲡科乐锦鳚鱼和亚鲹科虹鳟鱼的鱼体波数据, 得到对应鱼体波的行波系数分别为0.793和0.604。结果表明, 乐锦鳚鱼的鱼体波中含有较大的行波成分, 而虹鳟鱼鱼体波则含有较多的驻波成分。该结论从生物学上验证了鱼体波的复模态特性, 该特性与鱼体动力学特性以及游动模式有着密切关系。

鱼类; 游动模式; 鱼体波曲线; 复模态分解; 行波系数

0 引言

在自然界中, 85%的鱼类把身体和尾鳍当作主要推进器, 利用身体/尾鳍的左右摆动来产生反作用力并形成向后传播的鱼体波, 以实现快速高效的游动性能[1]。近年来, 随着仿生水下机器鱼研制工作的开展, 鱼类独特的游动性能吸引了越来越多的仿生学者, 其快速高效和高机动性的游动性能一直是研究的重点之一[2-3]。

1983年, Alexander等[4]发现鱼类的推进主要依赖于中间鳍和对鳍的摆动, 而后发现鱼类仅依靠尾鳍的摆动就可以实现推进。1984年, Breder[5]和Webb[6]等将鱼类游动分为身体/尾鳍(body and/or caudal fin, BCF)推进模式和中间鳍/对鳍(media and/or paired fin, MPF)推进模式两类, 该分类是根据鱼类游动中所使用的身体部位进行划分的。这种分类方法开创了人们研究鱼类游动模式的先河, 但对鱼类游动的描述较为直观, 分类也过于简单。

如图1所示, 鱼类BCF推进模式可根据参与摆动的尾体长度进一步细化为鳗鲡科、亚鲹科、鲹科和鲔科4个亚类[7]。以七鳗鱼为例, 鳗鲡科鱼类游动过程中大部分身体均参与弯曲摆动。但是对于鲹科和亚鲹科鱼类, 参与摆动的尾部占鱼长的1/2~2/3。以金枪鱼为例, 鲔科鱼类通常依靠尾鳍摆动实现推进, 游动速度快, 推进效率较高[8]。该分类方法虽然简单划分了鱼类BCF游动模式, 但并未考虑鱼体运动参数的变化情况, 如摆动频率、头部摆幅、鱼体波波长等信息。在不同的游动状态下, 鱼类参与摆动的长度也会有所变化[9]。另外, 文献[9]中提到鱼体的推进模式可分为波动推进和摆动推进, 但没有给出具体的分类方法。

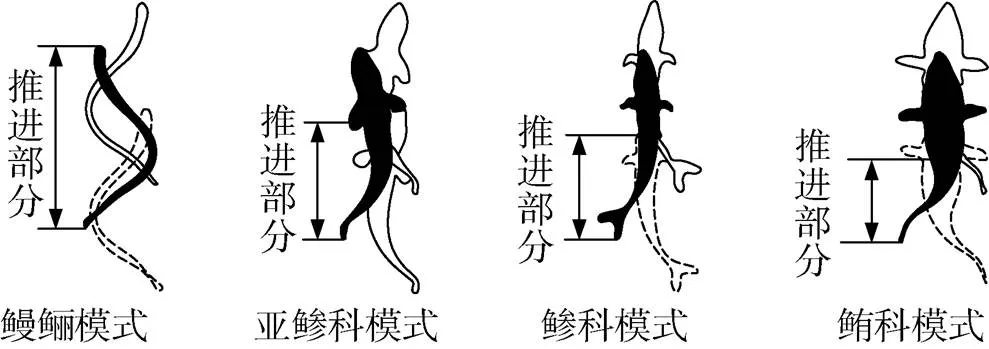
图1 BCF游动模式分类

目前, 仿生研究者逐渐开始关注鱼类运动学参数与游动性能之间的关系, 并将观测得到的生物学数据应用到鱼游机理的研究中。Videler等[10]记录了鲭鱼(Mackerel)和鳕鱼(Cod)鱼体波的变化情况, 并得到了鱼体波满足傅里叶级数形式的结论。Tytell等[11-12]通过分析美国鳗鱼(American eels)的鱼体波曲线, 发现幅值包络线的拟合方程和鱼体波波数, 该波数被用在七鳃鳗仿生机器鱼的设计中[13]。Videler等[14]总结了鱼类在稳态游动过程中波长的变化情况, 该研究也表明鱼类在不同游动状态下, 参与摆动的尾体长度会有所变化, 对应的游动性能也不相同。

研究表明, 目前BCF模式的游动性能与鱼体波参数、鱼体外形以及流体环境等因素存在复杂的关系。一方面, 鱼类的游动性能可通过鱼体波参数来评价, 如鱼体波波数、摆动幅值以及摆动频率等。另一方面, 鱼类游动时所产生的鱼体波曲线是由其身体的机械特性和流体环境来共同决定的。其中, 鱼体的机械特性(如弯曲刚度)可通过脊椎、肌肉和皮肤等生物组织来进行调节[14-15], 但是具体关系并不明确。

文中结合粘弹性力学和振动模态分析等基础理论, 以鱼体波曲线为研究对象, 通过研究其复模态振动特性来分析鱼类BCF推进模式。该研究对鱼体波曲线的研究以及鱼类游动机理的分析提出了新的认识, 也可为高性能仿生水下摆动推进机构的研制提供新的思路。

1 鱼体波复模态特性

1.1 鱼体波曲线

在自然界中, 鱼类利用其颉抗肌群产生粘弹性力, 并使各脊椎发生相对旋转, 整体表现为脊椎的弯曲曲线, 如图2所示。

图2 鱼体波示意图

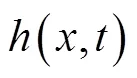
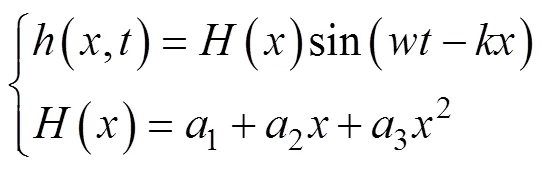
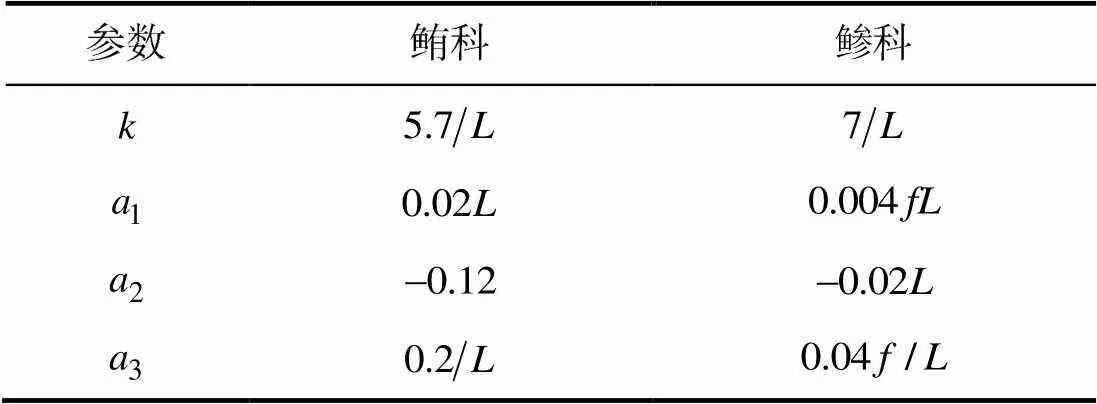
表1 鲔科和鲹科鱼类的鱼体波参数

以长度0.26 m的鲔科鱼类为例, 当其摆动频率为2 Hz时, 对应的鱼体波曲线如图3所示。图中单位BL为体长(body length),为摆动周期,为时间。

图3 摆动周期内鲔科鱼类鱼体波曲线

1.2 鱼体波复模态特性

从振动模态的角度看, 鱼类的游动实质是粘弹性鱼体在流体中的强迫振动。由于鱼体截面的非线性变化以及机械物理特性的复杂性, 对鱼体动力学特性的分析较为复杂。为了便于说明鱼体波的复模态特性, 文中将鱼体简化为等截面粘弹性梁, 该简化过程虽然不能准确给出鱼体波形成机理, 但是能够定性地分析鱼体波的复模态动力学特性。

根据振动模态理论[17], 当等截面粘弹性梁的动力学系统为比例阻尼系统或无阻尼系统时, 对应的方程为

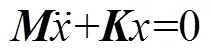
式中:为系统质量矩阵;为系统刚度矩阵。求解得到的波动方程形式为

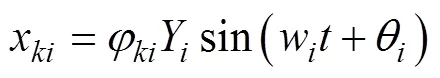
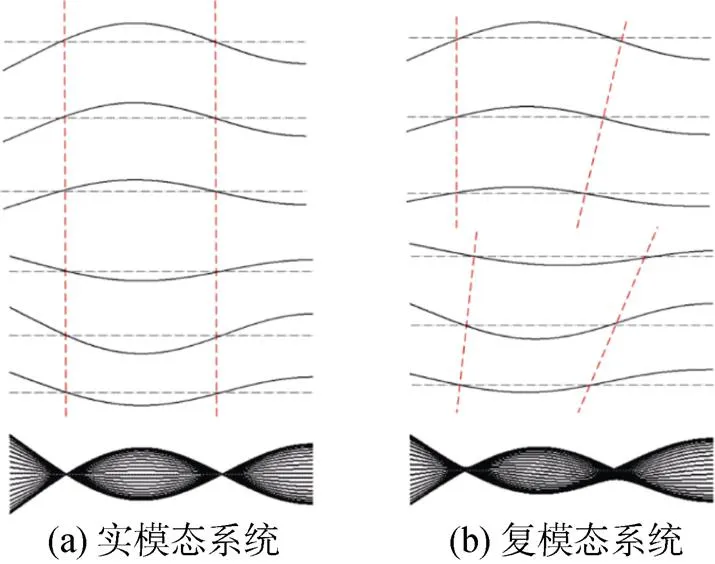
图4 半个摆动周期内实模态和复模态梁变形曲线

当动力学系统为一般阻尼系统时, 其模态矢量是复数, 对应的是复模态系统, 方程为

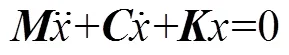
式中,为系统阻尼矩阵, 对应解的形式为

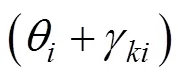
相类比, 粘弹性鱼体的动力学系统为一般阻尼系统时, 鱼体波对应的是复模态振型, 会产生行波形式的鱼体波。该分析间接表明, 鱼体波本质为鱼体振动对应的复模态振型, 可以为鱼体波的复模态特性研究给出理论参考。

2 鱼体波复模态正交分解方法

采用复模态正交分解(complex orthogonal decomposition, COD)方法来分析鱼体波的复模态特性。COD方法是特征正交分解方法(proper orthogonal decomposition, POD)的通用表达[18-19]。POD方法是一种用于提取模态信息的工具, 常用于驻波分析。而COD方法常应用在行波分析中, 适合BCF游动模式鱼类运动情况的分析。

首先, 将鱼体波曲线在不同位置和时间点进行数值离散, 得到矩阵方程为

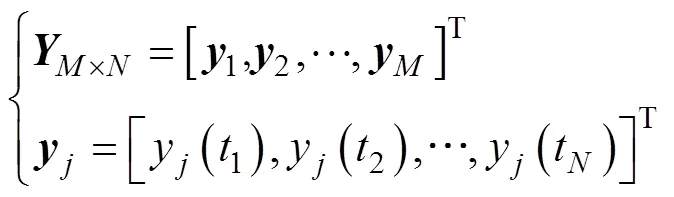
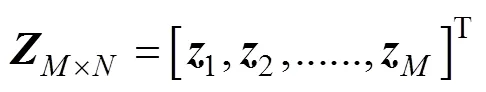
根据COD方法, 建立包含鱼体波信息的特征方程, 具体为

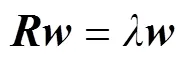
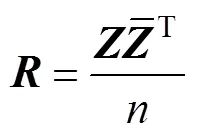
3 鱼体波实例分析

选择乐锦鳚鱼(Pholis Laeta)和虹鳟鱼(Rainbow Trout)2种不同类型的鱼体波来进行实验研究, 采用COD方法来分析鱼体波曲线, 通过行波系数来评价曲线的纯行波和纯驻波分量, 以验证鱼体波的复模态特性。

3.1 乐锦鳚鱼鱼体波分析

乐锦鳚鱼是鳗鲡科鱼类, 身体细长且全身参与摆动。实验中, 鱼体长度为0.4 m, 以约1.5 BL/s的速度从左向右游动, 如图5所示。

图5 乐锦鳚鱼在单位周期内的游动过程

通过逐帧分解乐锦鳚鱼在稳态游动时所拍摄的视频, 提取出鱼体的游动轨迹, 然后选定坐标系, 将不同图片中鱼体波的位置进行平移, 得到乐锦鳚鱼的鱼体波曲线, 如图6所示。图中, 鱼体波摆幅由头部逐渐向尾部增大, 鱼体尾部的摆幅可达0.15 BL。

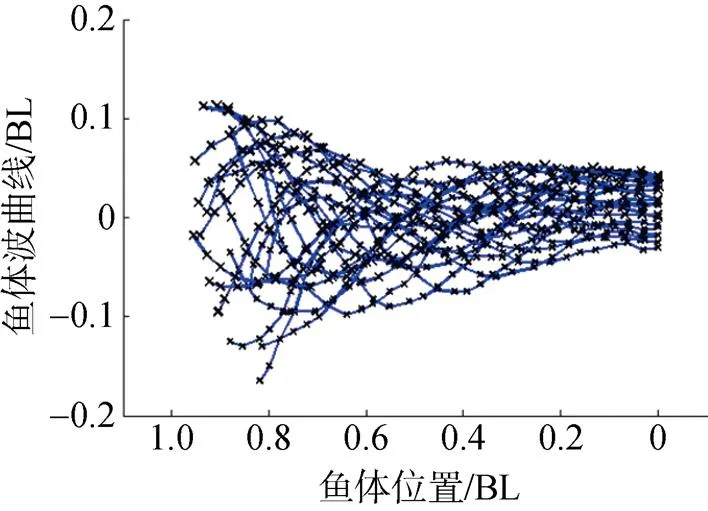
图6 乐锦鳚鱼鱼体波曲线

将乐锦鳚鱼鱼体波曲线进行复模态分解, 得到其纯行波部分和纯驻波部分如图7所示, 对应的行波系数为0.793。该结果表明, 乐锦鳚鱼鱼体波的行波系数较大, 其行波成分占主导。

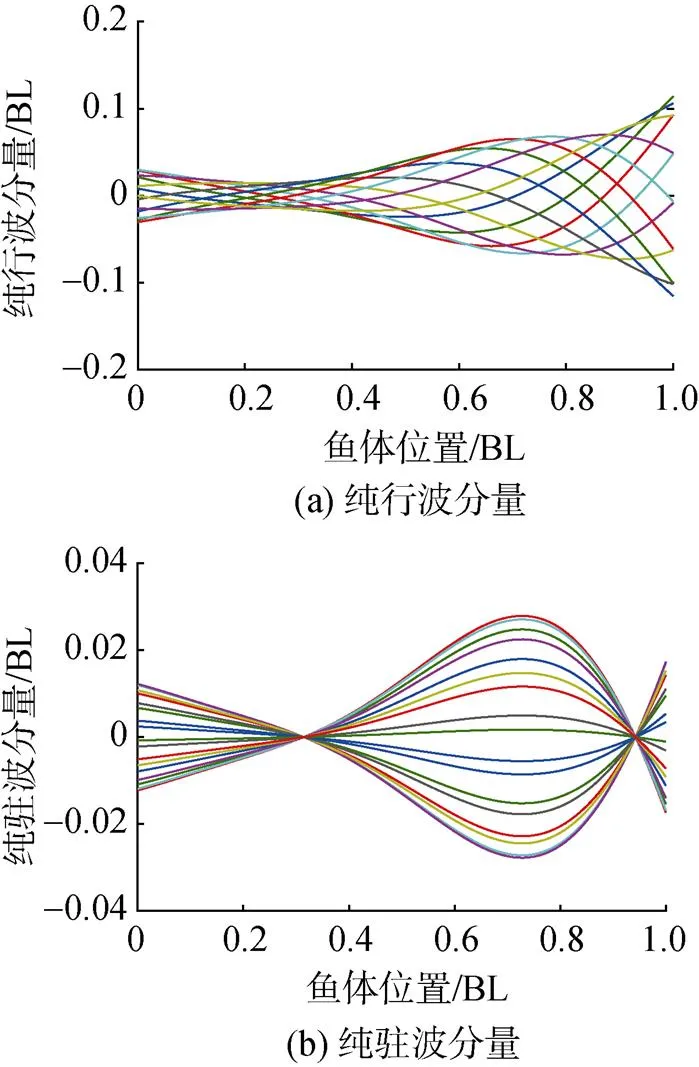
图7 乐锦鳚鱼鱼体波纯行波和纯驻波分量

3.2 虹鳟鱼鱼体波分析

选择0.35 m长的虹鳟鱼为研究对象, 同样通过拍摄其在稳态游动时的鱼体波变化来研究其复模态特性。虹鳟鱼在半个摆动周期内的游动状态如图8所示, 对应的鱼体波曲线如图9所示。

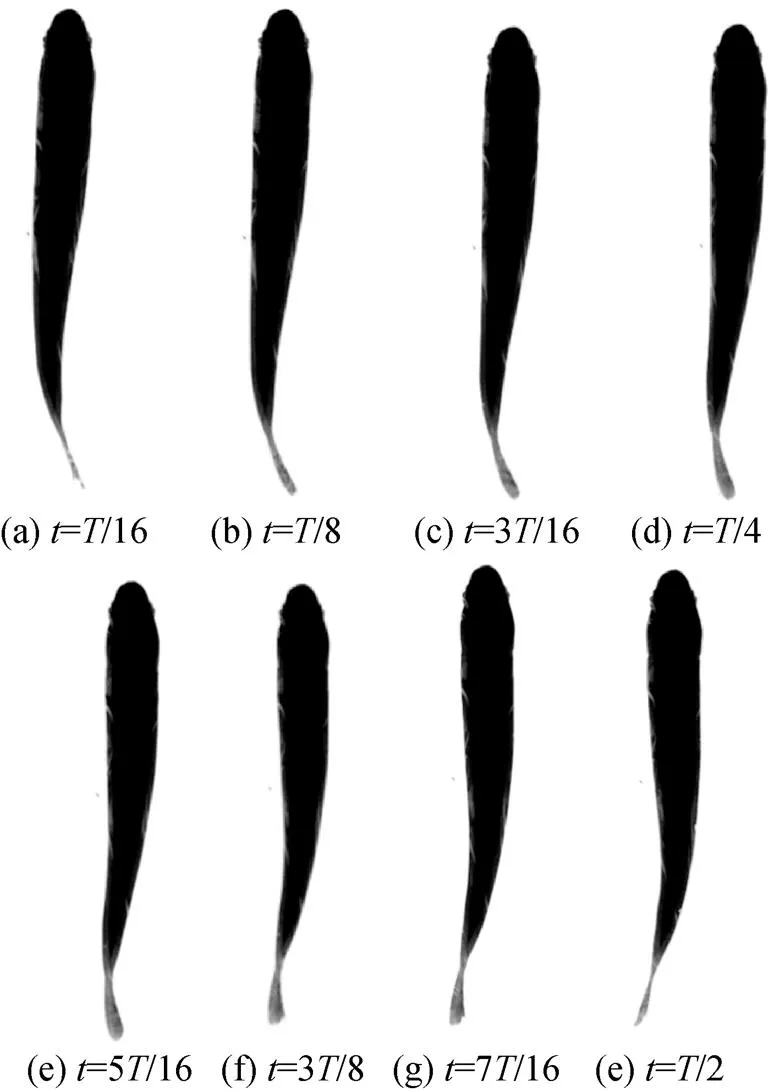
图8 虹鳟鱼在半个摆动周期内的游动过程

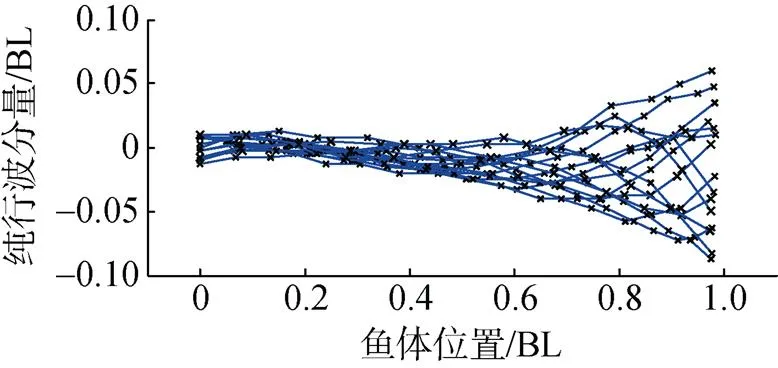
图9 虹鳟鱼鱼体波曲线

将虹鳟鱼鱼体波分解为纯行波和纯驻波两部分, 如图10所示。对应鱼体波的行波系数为0.604, 与乐锦鳚鱼相比, 虹鳟鱼鱼体波的纯驻波分量有所增加, 行波系数变小。

对比图7和图10发现, 乐锦鳚鱼大部分身体参与波动且波动的横向幅度大, 对应鱼体波的纯行波分量较大, 且鱼体头部摆幅较大。而虹鳟鱼头部摆幅较小, 主要依靠鱼体尾部的摆动来实现推进, 所以虹鳟鱼的纯驻波分量的驻点也靠近鱼体尾部。

4 鱼体波复模态特性分析

为了较为全面地介绍鱼体波的复模态特性, 结合前期工作, 分别从动力学、运动学和水动力学3方面介绍鱼体波的复模态特性, 具体关系如图11所示。

图10 虹鳟鱼鱼体波纯行波和纯驻波分量

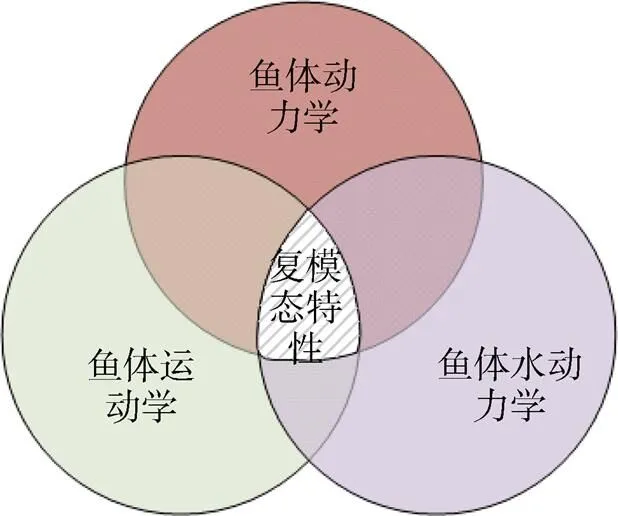
图11 鱼体波复模态特性与运动学、动力学和水动力学的关系

4.1 运动学特性

如图12所示, 通过分析40多种鱼体波曲线, 发现不同种类鱼体的鱼体波曲线有着不同的行波系数。鳗鲡科模式的鱼体波有着较大的行波分量, 对应着较大的行波系数, 范围为0.74~0.90; 鲔科模式对应的行波系数较低, 范围为0.36~0.64; 亚鲹科和鲹科模式鱼体波的行波系数范围为0.52~ 0.78。根据行波系数的分布范围, 鱼体游动模式可分为行波主导型、行波驻波混合型和驻波主导型3大类[20]。

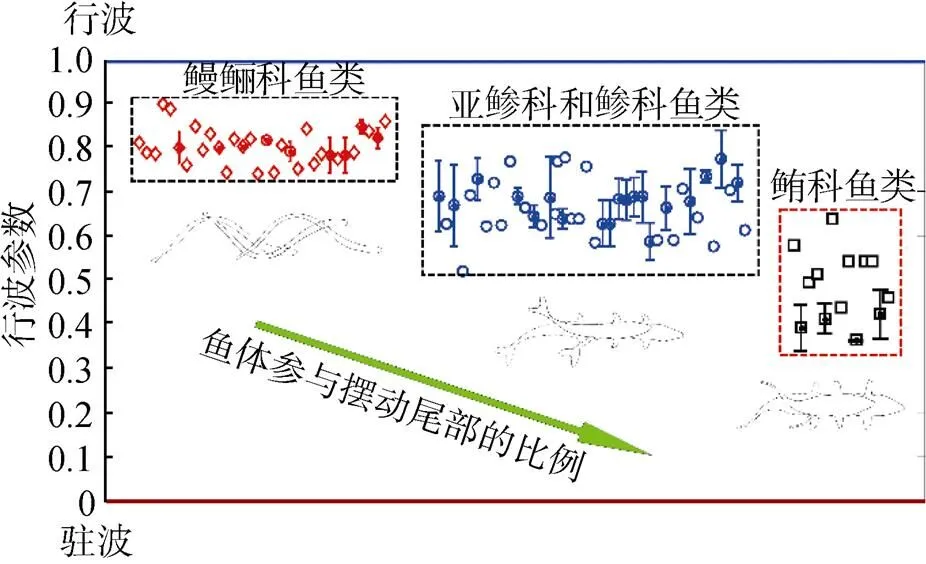
图12 摆动推进鱼类行波系数分布图

4.2 水动力学特性

通过建立鱼体的计算流体力学(computational fluid dynamics, CFD)游动模型发现, 在不同雷诺数环境中(雷诺数=400, 4 000, 40 000), 当鲹科鱼类鱼体波的行波系数在0.55附近时, 鱼体所受的推力达到最大值, 如图13所示。该结论与鲹科鱼类在自然界中选择的行波系数相接近。该研究也说明鱼体波的复模态特性与其游动性能有着直接关系[21]。

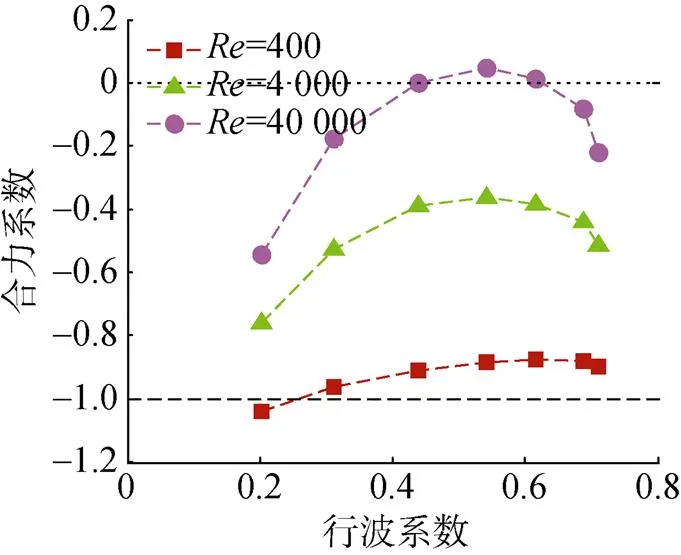
图13 三维鲹科鱼体所受推力与鱼体波行波系数之间的关系

4.3 动力学特性

根据Lighthill大摆幅细长体理论, 将柔性鱼体看作浸入到流体中的粘弹性梁。目前, 生物学研究表明, 鱼类可通过鱼体肌肉、肌腱以及其他生物组织来调节身体机械特性, 获得不同形式的鱼体波曲线, 进而获得快速高效的游动性能。虽然通过分析等截面粘弹性梁的动力学特性, 间接表明鱼体波具有复模态特性。但是, 鱼体波与鱼体刚度阻尼之间的关系不明确, 鱼体波的形成机理并不清楚。在考虑鱼体外形和刚度阻尼非线性变化的前提下, 下一步工作可建立BCF鱼类游动的动力学模型, 从理论上给出鱼体刚度、鱼体阻尼与鱼体波的具体关系[22-23]。另外, 还需要采用更先进的生物学测量方法来分析鱼体刚度阻尼的变化情况, 在此基础上进一步研制高性能仿生机器鱼。

5 结束语

文中结合生物学参数研究了鱼类身体/尾鳍推进模式中鱼体波的复模态特性。首先, 从振动模态的角度出发, 从粘弹性梁的动力学分析中提出了“鱼类的鱼体波实质是鱼体在流体环境中强迫振动的复模态振型”的观点, 然后通过分析乐锦鳚鱼和虹鳟鱼的鱼体波曲线, 并根据COD理论对鱼体波进行了分析, 验证了鱼体波的复模态特性。该研究可为后续波动推进模式鱼类的鱼体波特性研究提供参考。

[1] Lauder G V. Fish Locomotion: Recent Advances and New Directions[J]. Annual Review of Marine Science, 2015, 7: 521-545.

[2] Yu J, Wang M, Dong H, et al. Motion Control and Motion Coordination of Bionic Robotic Fish: a Review[J]. Journal of Bionic Engineering, 2018, 15(4): 579-598.

[3] Scaradozzi D, Palmieri G, Costa D, et al. BCF Swimming Locomotion for Autonomous Underwater Robots: a Review and a Novel Solution to Improve Control and Efficiency[J]. Ocean Engineering, 2017, 130: 437-453.

[4] Alexander R M, Webb P W, Weihs D. The history of fish mechanics[J]. Fish Biomechanics, 1983: 1-35.

[5] Breder C M. The Locomotion of Fishes[J]. Zoological, 1926, 4: 159-297.

[6] Webb P W. Form and Function in Fish Swimming[J]. Scientific American, 1984, 251(1): 72-79.

[7] Videler J J. Fish Swimming[M]. London: Chapman and Hall, 1993.

[8] Triantafyllou M S, Triantafyllou G S. An Efficient Swimming Machine[J]. Scientific American, 1995, 272(3): 64-71.

[9] Sfakiotakis M, Land D M. Review of Fish Swimming Modes for Aquatic Locomotion[J]. IEEE Journal of Oceanic Engineering, 1999, 24(2): 237-252.

[10] Videler J J, Hess F. Fast Continuous Swimming of Two Pelagic Predators, Saithe(Pollachius Virens) and Mackeral (Scomber Scombrus): a Kinematic Analysis[J]. Journal of Experimental Biology, 1984, 109: 209-228.

[11] Tytell E D, Carr J A, Danos N, et al. Body Stiffness and Damping Depend Sensitively on the Timing of Muscle Activation in Lampreys[J]. Integrative and Comparative Biology, 2018, 58(5): 860-873.

[12] Tytell E D, Lauder G V. The Hydrodynamics of Eel Swimming: Wake Structure[J]. Journal of Experimental Biology, 2004, 207: 1825-1841.

[13] Hultmark M, Leftwich M, Smits A J. Flow Field Measurements in the Wake of a Robotic Lamprey[J]. Experimental Fluids, 2007, 43: 683-690.

[14] Videler J J, Wardle C S. Fish Swimming Stride by Stride: Speed Limits and Endurance[J]. Reviews in Fish Biology and Fisheries, 1991, 1: 23-40.

[15] Tytell E D, Hsu C Y, Williams T L, et al. Interactions between Internal Forces, Body Stiffness, and Fluid Environment in a Neuromechanical Model of Lamprey Swimming[J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(46): 19832-19837.

[16] Alvarado P V Y. Design of Biomimetic Compliant Devices for Locomotion in Liquid Environments[D]. Cambridge, MA, USA: Massachusetts Institute of Technology, 2007.

[17] 曹树谦, 张文德, 萧龙翔. 振动结构模态分析: 理论、实验与应用[M]. 天津: 天津大学出版社, 2001: 18-22.

[18] Feeny B F. A Complex Orthogonal Decomposition for Wave Motion Analysis[J]. The Journal of Sound and Vibration, 2008, 310: 77-90.

[19] Feeny B F, Feeny A K. Complex Modal Analysis of the Swimming Motion of a Whiting[J]. Journal of Vibration and Acoustics, 2013, 135: 021004.

[20] Cui Z, Yang Z, Shen L, et al. Complex Modal Analysis of the Movements of Swimming Fish Propelled by Body and/or Caudal Fin[J]. Wave Motion, 2018, 78: 83-97.

[21] Cui Z, Gu X, Li K. CFD Studies of the Effects of Waveform on Swimming Performance of Carangiform Fish[J]. Applied Sciences, 2017, 7(2): 149.

[22] Yu Y Q, Howell L L, Lusk C, et al. Dynamic Modeling of Compliant Mechanisms Based on the Pseudo-Rigid-Body Model[J]. Journal of Mechanical Design, 2005, 127(4): 760-765.

[23] Cui Z, Jiang H. Design and Implementation of Thunniform Robotic Fish with Variable Body Stiffness[J]. International Journal of Robotics & Automation, 2017, 32(2): 109-116.

Complex Modal Decomposition and Characteristics Analysis of the Midline Motions of Swimming Fish Propelled by Undulating Body and Caudal Fin

CUI Zuo1, JIANG Hong-zhou2

(1. School of Aerospace Engineering, Guizhou Institute of Technology, Guiyang 550003, China; 2. School of Mechatronic Engineering, Harbin Institute of Technology, Harbin 150001, China)

In nature, the majority of fishes obtain their extraordinary swimming abilities of fast speed and high efficiency by propagating their midline motions backward. In this paper, the midline motions and their complex modal characteristics are analyzed by the method of complex orthogonal decomposition(COD). From the perspective of modal analysis, the movement of a swimming fish is in essence the forced vibration of viscoelastic body in fluid environment, and the motions are of complex modal shapes. According to the COD method, the midline motions are decomposed into the travelling and standing components. The correlation coefficient of the real and imaginary parts of complex modal shape is used to define the travelling index. Based on the analysis of the motions of two kinds of anguilliform fish(Pholis Laeta) and subcarangiform fish(Rainbow Trout), the travelling indexes of their midline motions are 0.793 and 0.604, respectively. It is shown that the midline motions of Pholis Laeta contain a large proportion of travelling wave, while the midline motions of Rainbow trout contain a larger proportion of standing wave. These biological results verify the complex modal characteristics of the midline motions, and the complex modal characteristics have close relation to the dynamic properties of fish body and the swimming patterns.

fish; swimming pattern; midline motions; complex modal decomposition; travelling index

TP242; TB301.2

A

2096-3920(2020)02-0119-07

10.11993/j.issn.2096-3920.2020.02.001

2019-07-04;

2019-08-16.

国家自然科学基金项目(51275127); 贵州理工学院学术新苗项目(黔合字[2017]5789-20); 高层次人才科研启动项目(XJGC20190956).

崔 祚(1988-),男, 博士, 副教授, 主要研究方向为水下柔性机器人和计算流体力学等.

崔祚, 姜洪州. 摆动推进鱼类鱼体波复模态分解及其特性分析[J]. 水下无人系统学报, 2020, 28(2): 119-125.

(责任编辑: 许 妍)