布站几何对深海时差定位精度分布特性的影响
张 旭, 李智生, 邱仁贵, 董 楠
布站几何对深海时差定位精度分布特性的影响
张 旭1, 李智生1, 邱仁贵2, 董 楠1
(1. 中国人民解放军91550部队, 辽宁 大连, 116023; 2. 中国人民解放军91650部队, 广东 广州, 510320)
为在深海较大区域实现海上无源目标的可靠水声定位, 测量设计中需对预选布站几何条件下的精度和覆盖特性进行有效估计。针对这一问题, 提出一种适用于多基站时差交会水声定位体制的精度分布特性仿真分析方法。以北太平洋中部海区的环境条件构设仿真场景, 采用BELLHOP高斯束射线模型计算声场, 应用Monte-Carlo方法迭加主要随机误差并传递到定位结果, 通过网格化和大子样计算分别得出4基站、5基站和6基站3类典型几何构型的均方根误差(RMSE)空间分布。分析表明, 在会聚区声信道条件下利用直达波与一次海底反射波进行定位性能有明显差异, 前者精度相对较高, 后者覆盖范围相对较大。直达波定位精度由阵中心区域向阵边缘区域逐渐减小, 而一次海底反射波定位则在阵中心数千米区域出现一个精度下降区。在处于顶角位置的基站失效或位于中心位置的基站偏移2种情况下, RMSE呈非对称分布, 仅在密集交会的局部区域有相对较高的精度, 不能保证对全海区有效覆盖。与以往的研究相比, 提出的方法满足深海条件下布站几何对精度分布和覆盖特性影响的评估与分析需求, 可为测量系统的设计与应用提供参考。
水声定位; 精度分布; 布站几何; 多基站; 覆盖特性; 深海
0 引言
采用多基站交会方式对海上无源声目标进行定位时, 基站的几何构型是决定测量精度的重要因素。在满足最低解算条件的基础上, 增加冗余基站通常可对改进定位精度有所贡献。但在实际海上作业中, 可增加的冗余基站总是有限的, 大规模的密集布站往往难以实施(特别是在远离岸站的深海区域), 在这种情况下, 布站几何的设计和优化就成为一个重要问题。已有报道讨论了四边形阵[1-2]、三角形阵[3]、圆形阵[4]等典型几何构型条件下的定位性能, 但现有报道大多针对浅海工况, 而对深海条件下的定位特性与布站几何的相关性问题关注较少。
与基于方位交会的被动定位方法[5]相比, 时差交会方法[6]因具有更好的精度特性, 较适用于深海大范围海区的被动声目标定位测量。深海与浅海的声信道条件明显不同[7-8], 声信息的到达方式和可检测程度随之变化, 需要结合深海声传播规律考虑相应的定位解算问题。哈尔滨工程大学曾在20世纪70年代末研制出我国第1套用于深海无源声目标定位测量的水声系统[9]。近年来, 随着深远海运载技术的不断发展, 对于深海测试保障条件提出了更高的要求, 需发展多场景、全区域精度分析方法以支撑测量系统论证设计。尽管深海无源声目标的定位方法不断发展, 但从海上试验结果的报道来看, 对于数十千米的测量范围在稀疏布站条件下获取较高精度仍较为困难[10-11]。近期关于深海时差定位特性的报道揭示了深海条件下双曲线交会呈现出与收-发条件和声传播相关的变异性[12], 但对于测量海区全区域精度分布特性与布站几何的相关关系问题尚未开展研究。
文中针对在深海数十千米范围内利用水下接收器到达时差定位水面声目标的工况, 通过数值仿真方法分析得出直达波与一次海底反射波的覆盖特性与精度分布特性, 初步建立了对深海声信道条件下的时差定位性能与布站几何关系的认识, 提出的方法和得到的结果与以往浅海背景下的研究有较明显的不同。
1 工况条件假设
假设测量作业的工况条件如图1所示。

图1 定位测量工况示意图
1) 要求对16 km×16 km测量海区内随机出现的、具有可识别声信号特征的水面目标进行定位, 获取其二维位置坐标。
2) 以无人水面船作为测量基站, 以吊放搭载的声接收器为测量载荷, 将现场获取的到达目标声信号以及测量基站、海洋环境等测量信息实时传输至地面站进行快速求解, 实现对随机水面目标的实时定位。其中, 测量元素为目标声信号的到达时差(由接收声信号估计到达时间, 每2个基站可形成一组到达时差); 无人水面船位置信息由卫星导航定位设备提供, 接收器与船体的相对位置信息由船载超短基线定位设备提供; 根据现场测量的声速剖面计算声场和声线追踪参数, 用于辅助解算。为在深海声信道条件下获取较大的直达波作用范围, 需将声接收器放置在较大的深度, 考虑到海上工程条件限制, 将最大布放深度设为1 000 m。
3) 测量海区选取在北太平洋中部, 水深5 500 m, 海底平坦, 声速剖面由WOA09数据集[13-14]给出的数据计算(见图2(a)), 环境不确定性引起的全深度平均声速起伏小于3 m/s。采用BELLHOP高斯束射线模型[15]计算声场, 声系统中心频率1 kHz, 掠射角范围0.1°~89°, 间隔0.18°, 水平方向计算范围为0~30 km, 网格间距0.1 km, 垂直方向计算范围为海面至海底, 网格间距20 m。计算得到的传播损失场见图2(b), 图中虚线处为接收深度, 声压通过全相干方式叠加。由图可见, 上述环境和收-发条件下的声信道样式为有弱表面波导的会聚区型声信道, 在30 km处约为1/2个会聚区的距离, 声场中亮区与影区边界相对分明, 亮区主要为直达波携带的能量, 影区则包括海底反射的声能以及少量衍射效应产生的声能。因此, 用于定位解算的声路径优先考虑直达波声路径(记为RR), 其次是一次海底反射波声路径(记为RB), 前者作用距离相对较近, 但信噪比高、时延误差小; 后者主要用于直达波作用距离之外的区域, 信噪比相对较低, 但作用距离大。对于文中工况, 直达波只能覆盖有限的区域, 而一次海底反射波则可覆盖全部测量海区。
4) 考虑到在深海离岸环境下开展测量作业的局限性, 将水面基站数量限定为不超过6个。
2 仿真算法设计
根据上述假设条件, 为开展不同几何布站条件下的测量区域精度分析, 基于Monte-Carlo方法建立以下仿真算法。
1) 建立坐标系
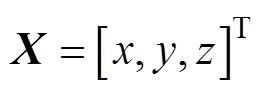

图2 声速剖面及声传播损失图
2) 计算声场和提取声信息
应用BELLHOP模型分别计算直达波和一次海底反射波的本征声线和传播损失。根据声呐方程, 到达各基站的信噪比与传播损失满足
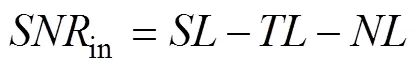
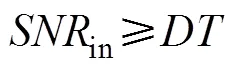
3) 迭加测量误差
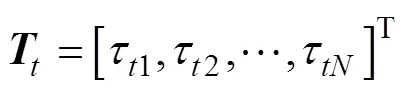
4) 估计待测参数
根据上述定义, 待测目标与基站之间的斜距可表示为

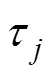
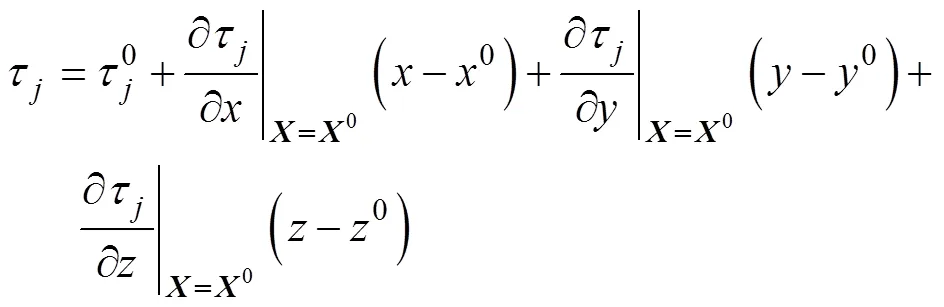
进而可建立目标相对于初始位置的时差变化与位置变化的关系式(若以基站1作为参考基站)[12]
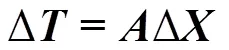
式中:

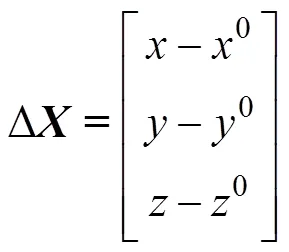
其中:

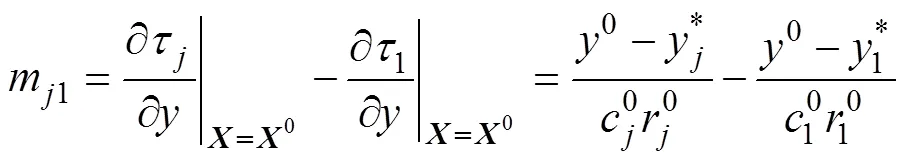
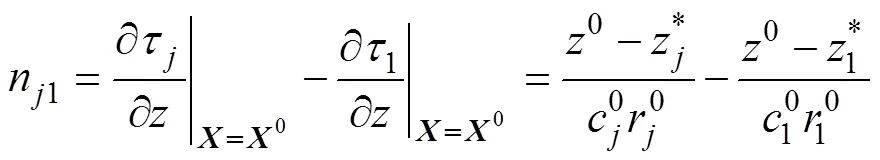
在此基础上, 可根据高斯-马尔可夫理论给出目标参数的估计值[16]
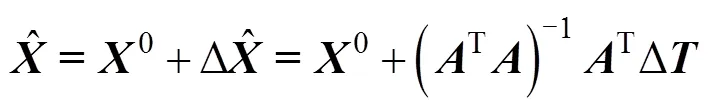
5) 历遍区域网格

3 典型布站情况仿真
以下分别考虑4基站、5基站和6基站3种典型的布站几何构型, 通过比较3种情况下覆盖特性和精度分布特性的差异分析布站几何对定位性能的影响。图3显示了上述3种布站几何, 并依据信噪比条件给出了直达波覆盖特性(根据前文假设, 一次海底反射波对测量海区是全覆盖的)。图中红点表示基站位置, 红线方框表示要求覆盖的测量区域; 图中数字表示直达波定位时参与交会解算的基站数, 其区域间差异由灰阶色差表示。

图3 3类典型布站几何及覆盖特性
为对比测量基阵内部与外部的精度变化, 将计算区域设为24 km×24 km(其中心区域为要求覆盖的16 km×16 km测量海区), 划分为201×201个格点, 按照上述仿真算法对格点逐一进行计算, 得到海区二维平面的精度分布矩阵。对每个格点进行1 000次抽样, 其统计结果可反映精度水平的总体特征。图4显示了3种布站条件下的RMSE分布, 图中区分了直达波与一次海底反射波定位的结果, 通过色标反映RMSE量值差异,黑点表示基站位置, 虚线方框表示要求覆盖的测量区域。
从宏观分布来看, 测量海区的定位精度主要有以下几方面特征:
1) 在会聚区声信道条件下, 接收器位于上层海洋时高信噪比的直达波所覆盖的区域总是有限的, 在4基站构型条件下, 如图4(a)所示, 基阵边缘附近有大面积直达波无法覆盖的区域, 随着有效基站数量的增加, 覆盖区域逐渐扩大且精度提升, 对于前文假设, 在6基站构型条件下, 如图4(e)所示, 可使测量海区内99%以上的区域达到优于30 m的精度;
2) 直达波与一次海底反射波定位性能有明显差异, 前者精度相对较高, 而后者覆盖范围相对较大;
3) 由于目标声信号的作用距离受信噪比限制, 测量海区内不同位置可接收的目标声信号作用距离与目标和基站的相对位置有关, 参与交会解算的基站组合空间变化使RMSE出现区域上的不连续, 在图中表现为由色差“跃变”形成的轮廓线;
4) 相对高精度区仅出现在基站包络范围之内, 而包络范围之外随交会点的减少精度迅速下降。
从精度分布特征来看, 直达波与一次海底反射波定位的RMSE可分为2个量值等级, 如图5所示, 图中横轴为沿基阵中心(0, 0)与测量海区西北(–8, 8)连线方向。前者的精度主要在20~30m量级, 而后者主要在40~80 m之间变化。对于直达波定位, 最高精度出现在阵中心附近, 这是因为该区域参与交会的有效基站数最多, 且精度随基站数的增加进一步提升, 4基站构型条件下距中心5 km范围内的RMSE为20~25 m, 而6基站构型条件下减小到15~20 m, 对于一次海底反射波定位, 当阵中心附近有基站时, 如图4(d)和图4(f)的情况, 从基阵中心到基阵边缘精度随距离不是单调变化, 在基阵中心2.5 km范围内RMSE出现一个显著增加的区域, 其量值可达70~80 m, 而在这个区域之外RMSE下降到40~50 m, 此后呈现随距离增加的趋势, 到10 km之外RMSE迅速增大到80 m以上。该现象的出现与本征声线及等效声速的特性有关, 在中心附近一次海底反射波的到达时延与直达波的到达时延相差可达数秒的量级, 等效声速减小到每秒数百米, 代入解算时相对于直达波的等效声速相对较高(约1400~ 1500 m/s)的情况其二次曲线交会特性明显变差; 随着距离增加, 一次海底反射波的等效声速不断增大, 与直达波的差值逐渐缩小, 低等效声速的影响随之减弱。

图4 3类典型布站几何条件下的X-Z平面RMSE分布
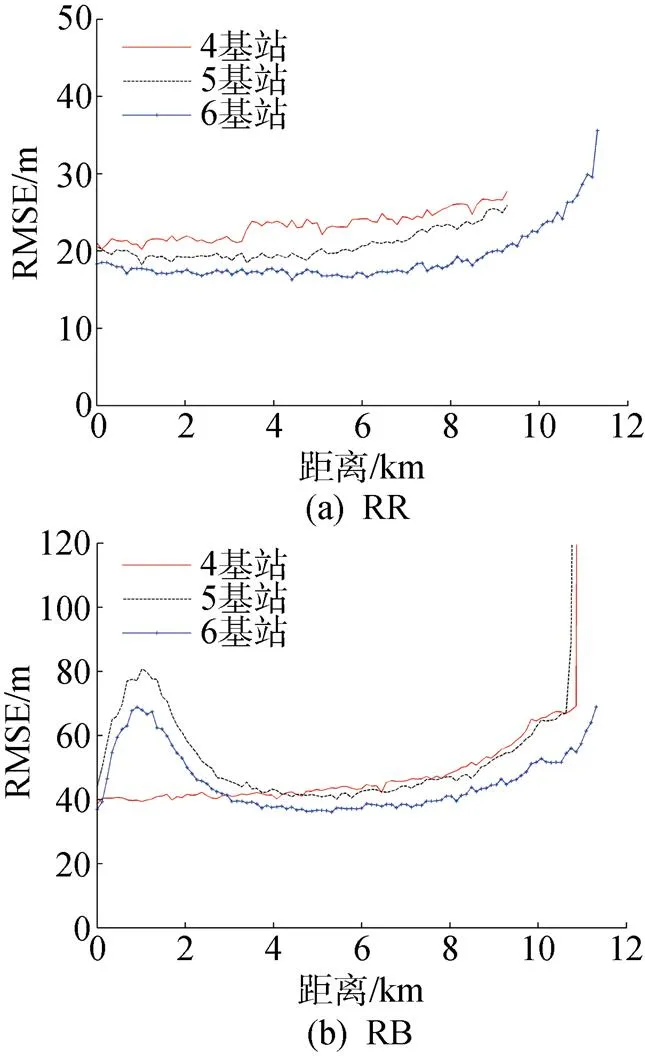
图5 RR与RB定位的RMSE曲线比较
表1和表2给出了上述算例中RMSE的分位数统计及RMSE达到某一精度水平的覆盖区域百分比。根据表1, 在4基站构型条件下, 若采用直达波定位, 有80%的区域(0.1分位数与0.9分位数之间)RMSE位于21.2~26.1 m之间, 若采用一次海底反射波定位, 则RMSE增大到40.9~52.9 m; 在5基站构型和6基站构型条件下(仍考虑80%区域), 直达波定位的RMSE分别减小了约4 m和6 m, 而一次海底反射波定位分别减小了约1 m和6 m, 说明从4基站构型到6基站构型无论是直达波定位还是一次海底反射波定位, 定位精度都有明显提升。根据表2, 若采用直达波定位并将RMSE优于30 m划定为高精度区, 4基站构型条件下仅有51.3%的区域达到此精度, 而5基站构型和6基站构型条件下分别为87.7%和99.6%; 若将RMSE优于50 m划定为可接受的精度, 4基站构型条件下的覆盖区域仍为51.3%(相对于RMSE优于30 m的情况没有提升), 而5基站构型和6基站构型则分别提升至97.3%和100%, 说明从4基站到6基站不仅提升了精度, 而且定位覆盖性能也有显著提升。对于一次海底反射波定位, 5基站构型和6基站构型条件下由于基阵中心的精度变差, 整体定位性能不及直达波, 而4基站构型条件下若可接受的精度指标下降, 则覆盖特性可明显提升, 例如若要求达到的RMSE标准从优于30 m下降至优于50 m, 则覆盖范围从0提升到79.1%。
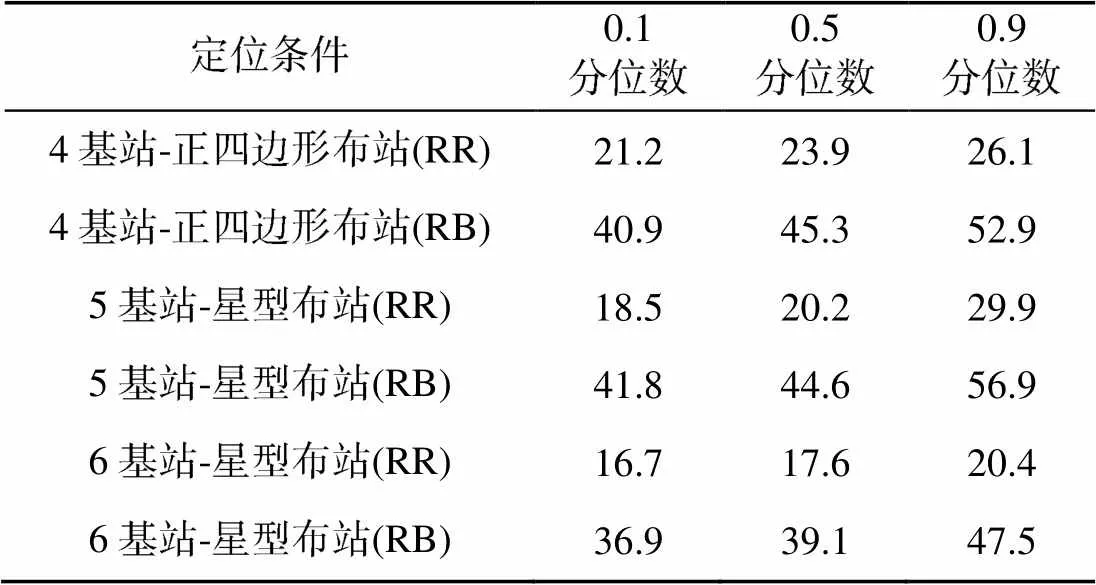
表1 不同定位条件下RMSE的分位数统计(单位: m)

表2 不同定位条件下RMSE优于某一精度水平的区域占测量区域的百分比(单位:%)
综合考虑上述3类布站几何, 4基站构型的覆盖能力对于16 km×16 km测量海区显得不足, RMSE优于30 m的区域仅接近50%; 相比之下, 5基站构型和6基站构型的覆盖能力相对较好。但若进一步考虑深海离岸作业实施上的困难性, 在要求精度允许的条件下(如要求RMSE优于50 m的区域不低于90%, 或RMSE优于30 m的区域不低于80%等), 5基站构型比6基站构型缩减了一个需要运载的测量平台, 在工程应用层面更具合理性。
4 特殊布站情况讨论
上述讨论的3种情况均为对称型布站, 而在实际工况下很可能要求在非对称布站条件下进行测量。为检验算法对非对称布站的响应, 设置以下3种情况:
1) 构成外围基阵包络的基站中有单个基站失效引起的非对称布站几何;
2) 位于基阵中心的基站明显偏移引起的非对称布站几何;
3) 仅由局部子基阵形成的非对称布站几何。
图6~图8分别给出了3种情况下的案例, 并通过直达波覆盖特性及RMSE分布图进行说明。
4.1 单个基站失效
分别考虑4基站、5基站和6基站构型中位于轴和轴正向的顶角附近的基站失效带来的影响。如图6所示, 其中(a)~(c)为直达波定位时参与交会解算的有效基站数分布, (d)~(f)为对应的RMSE分布, 布站几何的不对称直接导致交会覆盖的不对称和精度分布的不对称。在4基站条件下, 只有沿失效基站反向的小部分区域才有定位结果, 且精度显著下降, RMSE增大到30 m以上; 在5基站和6基站条件下, 由于有中心基站的补充, 覆盖区域扩大, 精度也随之提升, 6基站条件下相对高精度区达到测量海区的50%以上。但整体来看, 在外围基阵包络关键节点基站失效的情况下, 直达波定位无法覆盖到整个测量海区, 且有相当大的区域精度较差。
4.2 中心基站偏移
考虑5基站条件下位于基阵中心的基站分别向轴正向、轴正向和-平面45°方位偏移4 km时带来的影响。如图7所示, 其中(a)~(c)为直达波定位时参与交会解算的有效基站数分布, (d)~(f)为对应的RMSE分布。中心基站的位置变化对于相对高精度定位区域的分布影响明显, 总体趋势是在基站相对密集的区域趋于压缩, 在基站相对稀疏的区域趋于扩展, 且与参与交会解算的基站数量密切相关。除基站密集交会的区域外, 大部分顶角区域和基阵包络区域普遍精度较差。
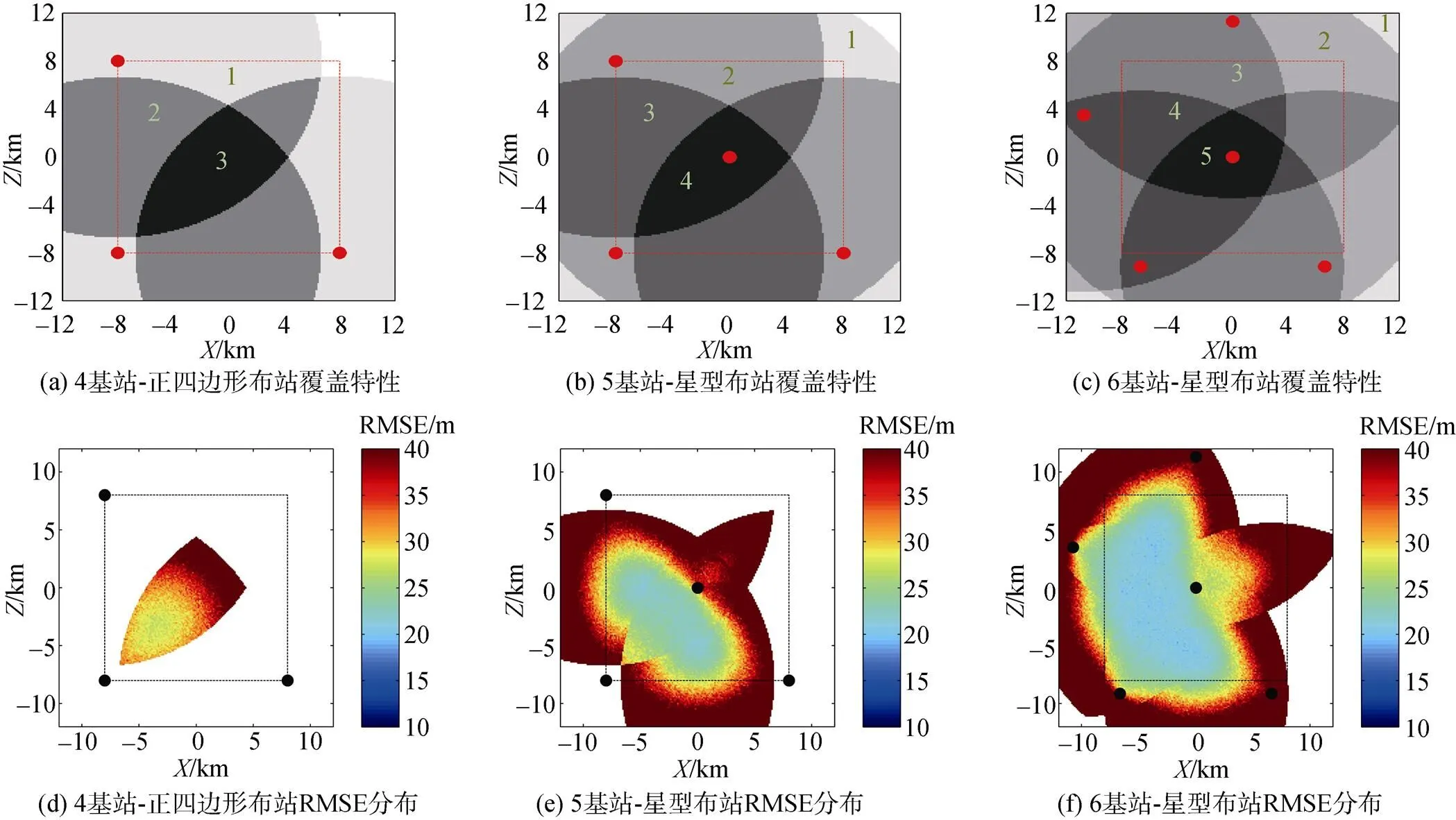
图6 3类单个基站失效情况下的覆盖特性及RMSE分布

图7 中心基站偏移情况下的覆盖特性及RMSE分布
4.3 子基阵定位
对称型布站条件下的5基站和6基站构型实际上均由若干3基站的子基阵构成, 分别考虑仅由这2种构型的子基阵定位所具有的性能。如图8所示, (a)~(b)为直达波定位时参与交会解算的有效基站数分布, (c)~(d)为对应的RMSE分布。由3基站构成的子基阵仅在三角形包络中心附近区域具有相对较高定位精度, 而在边缘附近定位性能较差。因此, 从测量海区直达波的覆盖性要求考虑, 由多个冗余基站形成的完整包络是重要保证, 而中心基站则为优化交会求解条件及提升定位性能有所贡献。
5 结束语
针对深海较大范围海区布站几何对海上随机目标水声定位性能影响分析问题, 提出一种基于多基站时差交会体制的全区域精度仿真分析方法, 初步解决了不同预选布站几何条件下的精度和覆盖特性估计问题, 可为测量系统论证设计与应用提供参考。
以4基站、5基站和6基站3种典型布站几何为例进行仿真分析。分析结果表明, 受会聚区声信道影响, 直达波与海底一次反射波定位性能有明显差异, 前者精度相对较高, 而后者覆盖范围相对较大。直达波定位阵中心区域精度优于阵边缘区域, 海底一次反射波定位则在阵中心附近出现一个2~3 km的精度下降区。从4基站到6基站, 直达波定位平均RMSE从23.9 m减小至17.6 m, 海底一次反射波定位平均RMSE从45.3 m减小到39.1 m, 直达波定位RMSE优于30 m的覆盖率从51.3%提升至99.6%。在处于顶角位置的基站失效或处于中心位置的基站偏移的情况下, RMSE出现非对称分布, 仅能在密集交会的局部区域获取相对较高的精度, 不能保证对全海区的覆盖性。
文中虽提出了一类适用于深海大范围海区时差定位精度评估的方法, 但仅考虑了简单声系统和二维声信道的情况, 并没有延伸到三维声环境、多源信息融合和声信号处理等问题, 更加精细、具体的模型和方法需要进一步开展研究。此外, 由于此类工况的特殊性, 现阶段还没有海上试验的结果支撑, 需要结合后续海上试验结果对提出的方法加以验证和改进。
[1] 贾云得, 冷树林, 刘万春, 等. 四元被动声敏感阵列定位模型分析和仿真[J]. 兵工学报, 2001, 22(2): 206-209. Jia Yun-de, Leng Shu-lin, Liu Wan-chun, et al. Modeling of Passive Acoustic Sensing with Four-sensor Array for Target Localization[J]. Acta Armamentarii, 2001, 22(2): 206-209.
[2] 金磊磊, 马艳. 任意四元阵的定位盲区讨论及误差影响[J]. 探测与控制学报, 2015, 37(2): 90-94.Jin Lei-lei, Ma Yan. Discussion on Blind Area and Error Effect of Arbitrary Four-element Array[J]. Journal of Detection & Control, 2015, 37(2): 90-94.
[3] 顾晓辉, 王晓鸣. 用双直角三角形阵对声目标定位的研究[J]. 声学技术, 2003, 22(1): 44-48.Gu Xiao-hui, Wang Xiao-ming. Location of Acoustic Target with Dual Right-triangles Array[J]. Technical Acoustics, 2003, 22(1): 44-48.
[4] 祝龙石, 庄志洪, 张清泰. 利用圆阵实现声目标的全空域被动定位[J]. 声学学报, 1999, 24(2): 204-209. Zhu Long-shi, Zhuang Zhi-hong, Zhang Qing-tai. An Omni-directional Passive Locatlization Technology of Acoustic Target with Plane Circular Array[J]. Acta Acustica, 1999, 24(2): 204-209.
[5] 王志刚, 陈韶华, 王维. 分布式基阵联合定位算法仿真分析[J]. 水下无人系统学报, 2018, 26(5): 433-438. Wang Zhi-gang, Chen Shao-hua, Wang Wei. Simulation Analysis of Joint Localization Algorithm Based on Distributed Arrays[J]. Journal of Unmanned Undersea Systems, 2018, 26(5): 433-438.
[6] 李韦华, 薛飞, 马锦垠. 时延差双曲面定位方法在鱼雷入水点测量中的应用[J]. 鱼雷技术, 2015, 23(6): 420-422. Li Wei-hua, Xue Fei, Ma Jin-yin. Application of Localization Method Based on Time Delay Difference and Hyperboloid to Torpedo Water-entry Point Measurement[J]. Torpedo Technology, 2015, 23(6): 420-422.
[7] Brekhovskikh L M, Lysanov Y P. Fundamentals of Ocean Acoustics[M]. 3rd ed. New York: AIP press, 2003.
[8] 杨坤德, 李辉, 段睿. 深海声传播信道和目标被动定位研究现状[J]. 中国科学院院刊, 2019, 34(3): 314-320.Yang Kun-de, Li Hui, Duan Rui. Research on Acoustic Propagation and Passive Localization in Deep Water[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(3): 314-320.
[9] 孙大军, 郑翠娥, 崔宏宇, 等. 水下传感器网络定位技术发展现状及若干前沿问题[J]. 中国科学: 信息科学, 2018, 48(9): 1121-1136. Sun Da-jun, Zheng Cui-e, Cui Hong-yu, et al. Developing Status and Some Cutting-Edge Issues of Underwater Sensor Network Localization Technology[J]. Scientia Sinica: Informationis, 2018, 48(9): 1121-1136.
[10] 陈连荣, 彭朝晖, 南明星. 高斯射线束方法在深海匹配场定位中的应用[J]. 声学学报, 2013, 38(6): 715-723. Chen Lian-rong, Peng Zhao-hui, Nan Ming-xing. The Application of Gaussian Beam Method in Deep Ocean Matched-Field Localization[J]. Acta Acustica, 2013, 38(6): 715-723.
[11] 吴俊楠, 周士弘, 张岩. 利用深海海底反射声场特征的水面声源被动测距[J]. 中国科学: 物理学力学天文学, 2016, 46(9): 76-82. Wu Jun-nan, Zhou Shi-hong, Zhang Yan. Passive Ranging of Surface Source Using Bottom Bounced Sound in Deep Water[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2016, 46(9): 76-82.
[12] 张旭. 深海分层介质中的无源声定位时差交会特性[J]. 科学通报, 2019, 64(24): 2523-2536.Zhang Xu. Time Difference Intersection Characteristics of Passive Underwater Acoustic Localization in the Stratified Deep Sea[J]. Chinese Science Bulletin, 2019, 64(24): 2523-2536.
[13] Locarnini R A, Mishonov A V, Antonov J I, et al. World Ocean Atlas 2009 Volume 1: Temperature[R]. Washington, D.C.: S. Levitus, Ed., NOAA Atlas NESDIS 68, U.S. Government Printing Office, 2010.
[14] Antonov J I, Seidov D, Boyer T P, et al. World Ocean Atlas 2009, 2(Salinity)[R]. NOAA Atlas NESDIS 69. Washington D C: Government Printing Office, 2010.
[15] Porter M B, Bucher H P. Gaussian Beam Tracing for Computing Ocean Acoustic Fields[J]. J. Acoust. Soc. Am, 1987, 82: 1349-1359.
[16] 刘利生, 吴斌, 吴正容, 等. 外弹道测量精度分析与评定[M]. 北京: 国防工业出版社, 2010: 123-188.
[17] 张旭, 孙翱, 韩旭, 等. 水下垂向运动目标的海底多基站声定位方法及精度分析[J]. 声学学报, 2019, 44(2): 155-169. Zhang Xu, Sun Ao, Han Xu, et al. Acoustic Localization Scheme and Accuracy Analysis for Underwater Vertical Motion Target Using Multi-stations in the Seabed[J]. Acta Acustica, 2019, 44(2): 155-169.
Effects of Observation Geometry on Accuracy Distribution Characteristic of TDOA Localization System in Deep Sea
ZHANG Xu1, LIZhi-sheng1, QIU Ren-gui2, DONG Nan1
(1. 91550thUnit, the People’s Liberation Army of China, Dalian 116023, China; 2. 91650thUnit, the People’s Liberation Army of China, Guangzhou 510320, China)
To stably localize an acoustic target in a large area of deep sea, the accuracy and coverage characteristic are required to be evaluated under pre-selected observation geometry condition in the measurement system design. Aiming at this problem, a simulation method was presented for analyzing the distributional characteristics of accuracy in underwater acoustic localizationwith multiple base stations by time difference of arrival(TDOA). The climatological environment in the center of Northern Pacific was selected as background, and the sound field was calculated by BELLHOP Gaussian ray model. Main errors were randomly superimposed by Monte-Carlo method and propagated to finally estimated locations, such that the distribution of root mean square error(RMSE) was established by grid calculation with large samples under typical geometry condition of 4-receiver, 5-receiver or 6-receiver array. The results indicated that the localization performance using direct waves was clearly different from that using first-seabed-reflected waves, and the former was more accurate while the later was better in coverage. For the localization with direct waves, the accuracy was better in the central area of array than that in the marginal one. For the localization with first-seabed-reflected waves, the accuracy became worse in the area several kilometers around the center of array. In another case, the RMSE showed an asymmetric distribution when one corner station was invalid or the central station shifted, the relatively high accuracy area was confined to the active station number, but the full measurement area failed to be covered. Compared with the existing researches, this research provides an applicable way to evaluate and analyze the influence of observation geometry on accuracy distribution and coverage characteristic.
underwater acoustic localization; accuracy distribution; observation geometry; multiple base stations; coverage characteristic; deep sea
TB566; TJ630.33
A
2096-3920(2020)02-0139-10
10.11993/j.issn.2096-3920.2020.02.004
2019-06-17;
2019-07-08.
国家自然科学基金(61701504, 61971424).
张 旭(1982-), 男, 博士, 工程师, 主要从事水下测量技术、海洋信息应用技术研究.
张旭, 李智生, 邱仁贵, 等. 布站几何对深海时差定位精度分布特性的影响[J]. 水下无人系统学报, 2020, 28(2): 139-148.
(责任编辑: 许 妍)

